Mathematics
If find the value of :
(i) 2 - sin2 θ - cos2 θ
(ii)
Trigonometric Identities
10 Likes
Answer
Given:
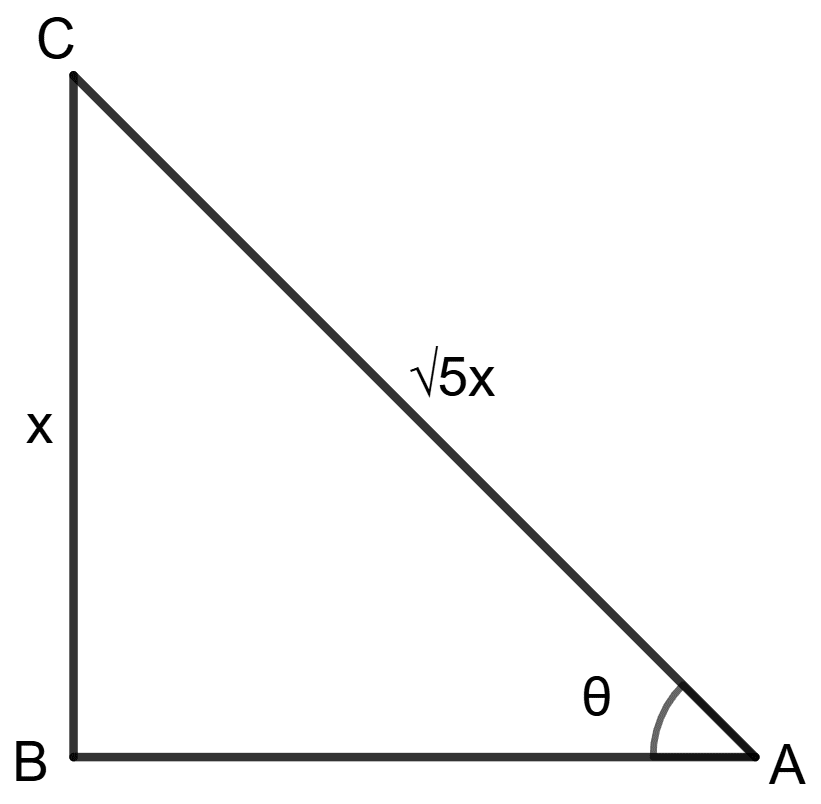
∴ If length of AC = x unit, length of BC = x unit.
In Δ ABC,
⇒ AC2 = BC2 + AB2 (∵ AC is hypotenuse)
⇒ (x)2 = (x)2 + AB2
⇒ 5x2 = x2 + AB2
⇒ AB2 = 5x2 - x2
⇒ AB2 = 4x2
⇒ AB =
⇒ AB = 2x
(i) sin θ =
cos θ =
Now,
2 - sin2θ - cos2θ
Hence, 2 - sin2θ - cos2θ = 1.
(ii)
Hence, = 3.
Answered By
4 Likes
Related Questions
Assertion (A): The value of sin2 30° - 2 cos3 60° + 2 tan4 45° is 2.
Reason (R): sin 30° = , cos 60° = , and tan 45° = 1
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
Assertion (A): If A = 30°, the value of 4 sin A sin (60° - A) sin (60° + A) = 1.
Reason (R): 60° - A = 30° and 60° + A = 90°.
A is true, but R is false.
A is false, but R is true.
Both A and R are true, and R is the correct reason for A.
Both A and R are true, and R is the incorrect reason for A.
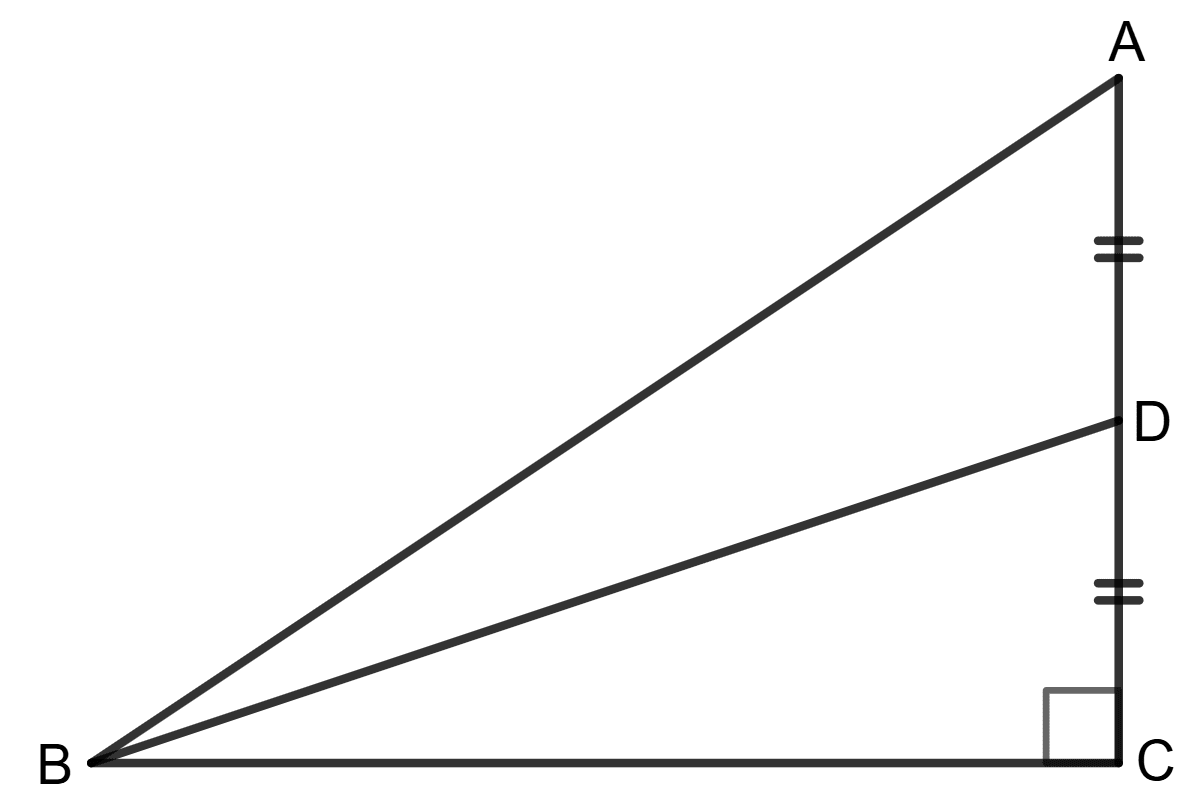
In the given figure; ∠C = 90° and D is mid-point of AC. Find :
(i)
(ii)
If 3 cos A = 4 sin A, find the value of :
(i) cos A
(ii) 3 - cot2 A + cosec2 A