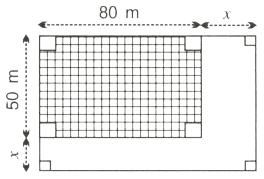
In the given figure; the area of unshaded portion is 75% of the area of the shaded portion. Find the value of x.

From figure,

Length of larger portion (L) = (80 + x) meters

Breadth of larger portion (B) = (50 + x) meters

Area of larger portion = L × B = (80 + x)(50 + x)

= 4000 + 80x + 50x + x²

= (x² + 130x + 4000) m².

Length of smaller portion (l) = 80 meters

Breadth of smaller portion (b) = 50 meters

Area of smaller portion = l × b = 80 × 50 = 4000 m²

Area of unshaded portion = Area of larger portion - Area of smaller portion

= x² + 130x + 4000 - 4000

= (x² + 130x) m².

Given,

Area of unshaded portion is 75% of the area of the shaded portion.

$\therefore 75\% \text{Area of Shaded portion = Area of unshaded portion} \\[1em] \Rightarrow \dfrac{75}{100} \times 4000 = x^2 + 130x \\[1em] \Rightarrow 3000 = x^2 + 130x \\[1em] \Rightarrow x^2 + 130x - 3000 = 0 \\[1em] \Rightarrow x^2 + 150x - 20x - 3000 = 0 \\[1em] \Rightarrow x(x + 150) - 20(x + 150) = 0 \\[1em] \Rightarrow (x - 20)(x + 150) = 0 \\[1em] \Rightarrow x - 20 = 0 \text{ or } x + 150 = 0 \\[1em] \Rightarrow x = 20 \text{ or } x = -150.$

Since, length cannot be negative.

∴ x = 20 meters.

Hence, x = 20 meters.