Physics
Light travels a distance of ‘10x’ units in time ‘t1’ in vacuum and it travels a distance of ‘x’ units in time ‘t2’ in a denser medium. Using this information answer the question that follows :
(a) ‘Light covers a distance of ‘20x’ units in time ‘t1’ in diamond.’ State true or false.
(b) Calculate the refractive index of the medium in terms of ‘t1’ and ‘t2’.
Refraction Plane Surfaces
5 Likes
Answer
(a) False because speed of light in vacuum is highest and diamond is a denser medium so speed of light will be lower and hence, it can not travel a distance 20x in diamond which is two times of distance travelled by light in vacuum.
(b) Given,
Distance travelled by light in vacuum = 10x
Time taken by light in vacuum = t1
Distance travelled by light in the medium = x
Time taken by light in diamond = t2
As,
and
then,
Answered By
3 Likes
Related Questions
(a) Why do we use red colour as a danger signal on the top of a skyscraper?
(b) The diagram below shows the path of a blue ray through the prism :
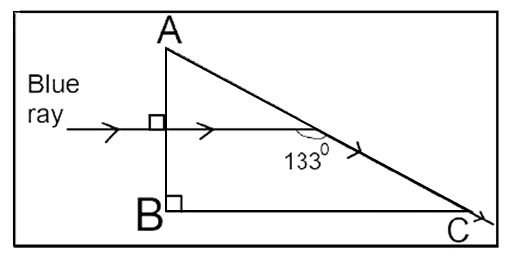
- Calculate the critical angle of the material of the prism for blue colour.
- What is the measure of the angle of this prism (A)?
- Which colour should replace the blue ray, for the ray to undergo Total Internal Reflection?
(a) Refractive index of glass with respect to water is . Find the refractive index of water with respect to glass.
(b) Name the principle used to find the value in part (a).
(c) If we change the temperature of water,then will the ratio remain the same? Write yes or no.
A monochromatic ray of light is incident on an equilateral prism placed at minimum deviation position with an angle of incidence 45° as shown in the diagram.
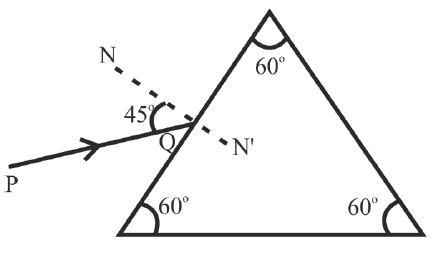
(a) Copy the diagram and complete the path of the ray PQ.
(b) State two factors on which the angle of deviation depends.
(a) Define Centre of Gravity.
(b) A hollow ice cream cone has height 6 cm.
- Where is the position of its centre of gravity from the broad base?
- Will its position change when it is filled completely with honey? Write Yes or No.