Mathematics
On seeing the below display board outside Pearl Stationary Shop, Chetan enters the shop to buy the following items:

| Pen | Pencil | Rainbow cover notebook | |
|---|---|---|---|
| Price | ₹5 each | ₹7 each | ₹ 200 each |
| Discount | 5% on a dozen pens | 10% on 20 pencils | ------ |
| Premium | - | - | ₹50 on each notebook |
| Items purchased | 1 dozen | 20 pencils | 5 |
| GST | 18% | 12% | 12% |
The shopkeeper handed over the bill to Chetan saying that he has given further discount of 2% on total bill. Chetan became so happy hearing about the discount that he did not check the bill until he reached home. He later found out that though shopkeeper has given 2% discount as promised, he had also mischarged uniform 18% GST on all the items.
(a) Calculate :
(i) total selling price of all the items as per the offers displayed on the board.
(ii) total amount to be paid by Chetan including GST with correct rates.
(iii) actual amount charged by the shopkeeper.
(b) Did the shopkeeper overcharge Chetan? Justify your answer
GST
55 Likes
Answer
(a)
For pen :
No. of pens purchased = 12
Price of 12 pens = ₹5 × 12 = ₹60
Discount (D) : 5% on dozen pens.
Price after discount = ₹ 60 - ₹ 3 = ₹ 57.
GST = 18% = = ₹ 10.26
Total price : ₹ 57 + ₹ 10.26 = ₹ 67.26
For pencil :
No. of pencils purchased = 20
Price of 20 pencils = ₹ 7 × 20 = ₹ 140
Discount (D) : 10% on 20 pencils.
Price after discount = ₹ 140 - ₹ 14 = ₹ 126.
GST = 12% = = ₹ 15.12
Total price : ₹ 126 + ₹ 15.12 = ₹ 141.12
For notebook :
No. of notebooks purchased = 5
Price of 5 notebooks = ₹ 200 × 5 = ₹ 1000
Premium (P) : ₹ 50 on each notebook
Total premium : ₹ 50 × 5 = ₹ 250.
Price after premium = ₹ 1000 + ₹ 250 = ₹ 1250.
GST = 12% = = ₹ 150.
Total price : ₹ 1250 + ₹ 150 = ₹ 1400.
(i) Total selling price of all items = ₹ 57 + ₹ 126 + ₹ 1250 = ₹ 1433.
Hence, total selling price = ₹ 1433.
(ii) Total price paid (including GST) = ₹ 67.26 + ₹ 141.12 + ₹ 1400 = ₹ 1608.38
Hence, total price paid (including GST) = ₹ 1608.38
(iii) On applying incorrect GST rates :
On pen :
Price after discount = ₹ 57.
GST = 18% = = ₹ 10.26
Total price : ₹ 57 + ₹ 10.26 = ₹ 67.26
On pencil :
Price after discount = ₹ 126.
GST = 18% = = ₹ 22.68
Total price : ₹ 126 + ₹ 22.68 = ₹ 148.68
For notebook :
Price after premium = ₹ 1250.
GST = 18% = = ₹ 225.
Total price : ₹ 1250 + ₹ 225 = ₹ 1475.
When the GST rate is applied as 18% uniformly, bill need to be paid by Chetan :
= ₹ 1475 + ₹ 148.68 + ₹ 67.26
= ₹ 1690.94
Discount given on total bill = 2%
= 33.82
Bill = ₹ 1690.94 - ₹ 33.82 = ₹ 1657.12
Hence, bill = ₹ 1657.12
(b) The bill should be of ₹ 1608.38 but instead it was of ₹ 1657.12
⇒ ₹ 1657.12 - ₹ 1608.38 = ₹ 48.78
Hence, the shopkeeper overcharged an amount of ₹ 48.78
Answered By
34 Likes
Related Questions
Using remainder and factor theorem, show that (2x + 3) is a factor of the polynomial 2x2 + 11x + 12. Hence, factorise it completely. What must be multiplied to the given polynomial so that x2 + 3x - 4 is a factor of the resulting polynomial? Also, write the resulting polynomial.
The sequence 2, 9, 16, ….. is given.
(a) Identify if the given sequence is an AP or a GP. Give reasons to support your answer.
(b) Find the 20th term of the sequence.
(c) Find the difference between the sum of its first 22 and 25 terms.
(d) Is the term 102 belong to this sequence?
(e) If ‘k’ is added to each of the above terms, will the new sequence be in A.P. or G.P.?
Given the equations of two straight lines, L1 and L2 are x - y = 1 and x + y = 5 respectively. If L1 and L2 intersects at point Q (3, 2). Find :
(a) the equation of line L3 which is parallel to L1 and has y-intercept 3.
(b) the value of k, if the line L3 meets the line L2 at a point P (k, 4).
(c) the coordinate of R and the ratio PQ : QR, if line L2 meets x-axis at point R.
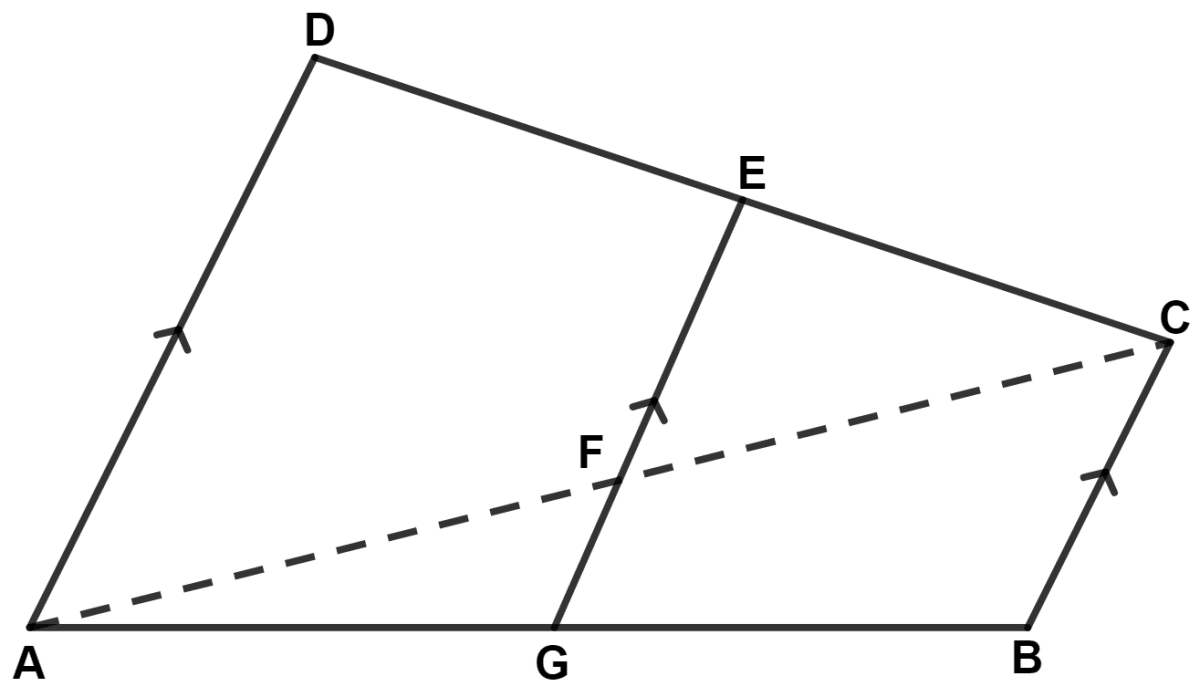
In the figure given below (not drawn to scale), AD ∥ GE ∥ BC, DE = 18 cm, EC = 3 cm, AD = 35 cm. Find :
(a) AF : FC
(b) length of EF
(c) area(trapezium ADEF) : area(Δ EFC)
(d) BC ∶ GF