Physics
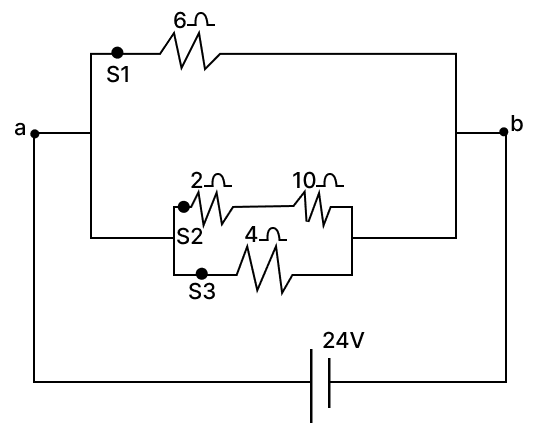
Which one of the switches, S1, S2 or S3, should be opened so that:
(a) total resistance is equal to 4 ohms.
(b) the total resistance is equal 3 ohms.
(c) the current through 4 ohms is 3⁄5th of the total current.
Current Electricity
11 Likes
Answer
(a) S3
(b) S1
(c) S2
Explanation:
Let R1= 6 Ω, R2= 2 Ω, R3= 10 Ω, R4= 4 Ω
If S3 is open: then R2 and R3 are in series
then Rs and R1 are in parallel
Total resistance is 4 Ω
If S1 is open: then R2 and R3 are in series
and Rs and R4 are in parallel:
Total resistance is 3 Ω
If S2 is open: then R1 and R4 are in parallel
Total resistance is 2.4 Ω
Total current drawn in circuit
Voltage across 4 Ω is 24 V
so, current through 4 Ω is
So, the current through 4 ohms is 3⁄5th of the total current.
Answered By
6 Likes
Related Questions
Read the excerpt from a story and answer the questions that follow:
On stage, a soft iron box sits atop a hidden copper coiled platform, conductive to electricity. I summoned a man who fancied himself a modern-day Hercules onto the stage and challenged him to lift the iron box. With ease, he lifted it up. Then, with a wave of my magic wand and a hidden switch activated, I said, "I'm going to take away your strength." When I asked him to lift the box again, he struggled, unable to budge it.
(a) Explain the secret behind the magic.
(b) If you are asked to design the same magic in your science lab, give the necessary circuit diagram.
(c) Give any one device that works on the same principle.
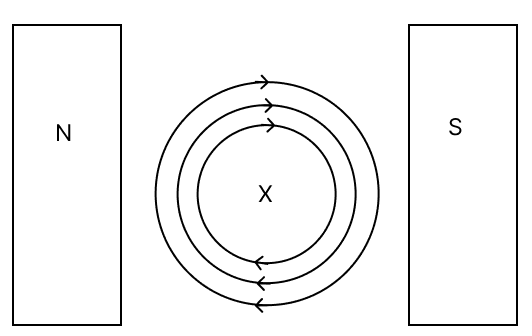
In the given diagram, X represents a conductor carrying current into the plane of the paper and kept in a magnetic field. N & S represent the poles of a magnet and concentric circles of the magnetic field produced by the conductor.
(a) State the direction of the force experienced by the conductor.
(b) Explain the cause of the above-said force.
(c) Name the law used to determine the direction of the force in the conductor.
Study the diagram and answer the following:
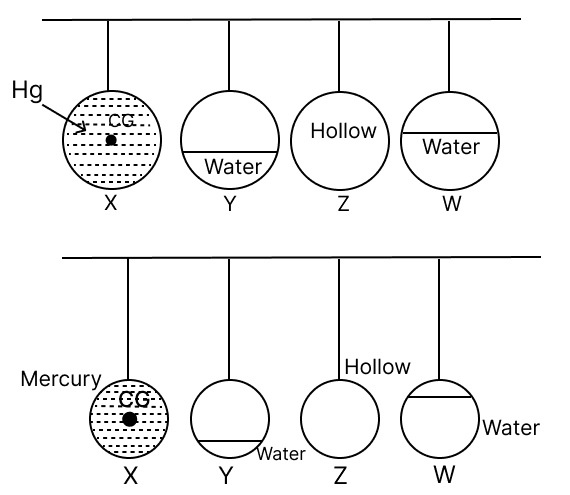
(a) Arrange the following pendulums according to their natural frequencies (use < > =).
(b) If Pendulum Z is initiated into oscillation, which pendulum among the others will exhibit the highest amplitude of vibration?
(c) Give reasons for your answer.
In the physics laboratory, various blocks of materials labelled A and B, each with masses ranging from 10 grams to 50 grams, are utilised to determine their respective heat capacities. Subsequently, a graph is plotted to depict the relationship between the heat capacity and the mass of the materials, as shown.
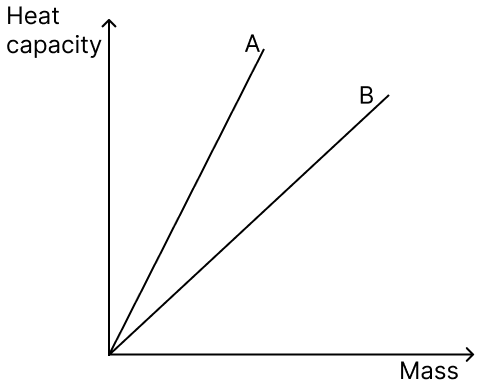
(a) Plot a graph illustrating the relationship between the mass and specific heat capacity of materials A and B.
(b) Which material is a relatively better conductor?