Mathematics
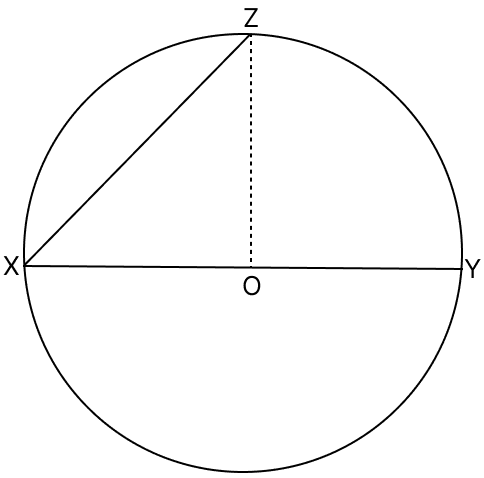
In the adjoining figure, O is the centre of a circle, XY is a diameter and XZ is a chord. Prove that XY > XZ.
Triangles
1 Like
Answer
From figure,
OX = OZ = OY [Radius of same circle]
We know that,
In a triangle, sum of any two sides is always greater than the third side.
In △XOZ,
⇒ OX + OZ > XZ
⇒ OX + OY > XZ (∵ OZ = OY)
⇒ XY > XZ
Hence, proved that XY > XZ.
Answered By
2 Likes
Related Questions
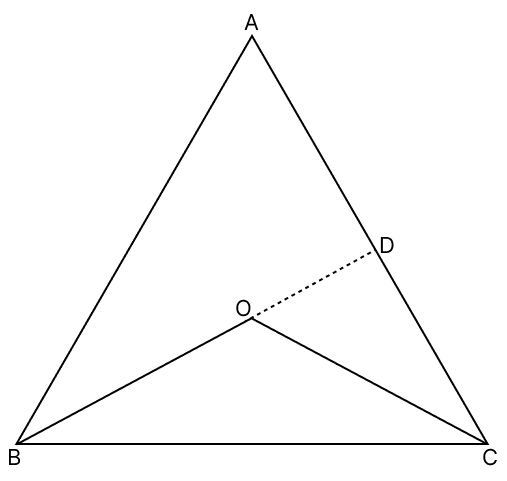
In the adjoining figure, in △ABC, O is any point in its interior. Show that: OB + OC < AB + AC
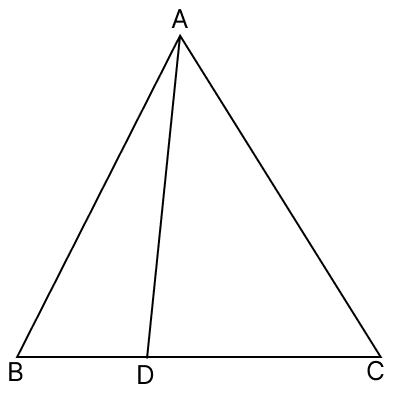
In △ABC, D is any point on BC. Prove that : AB + BC + AC > 2 AD.
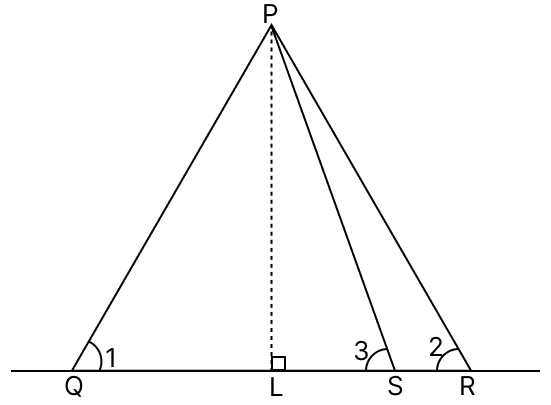
In the adjoining figure, PL ⊥ QR; LQ = LS and LR > LQ. Show that PR > PQ.
In the adjoining quadrilateral ABCD, AB is the longest side and DC is the shortest side. Prove that :
(i) ∠C > ∠A
(ii) ∠D > ∠B