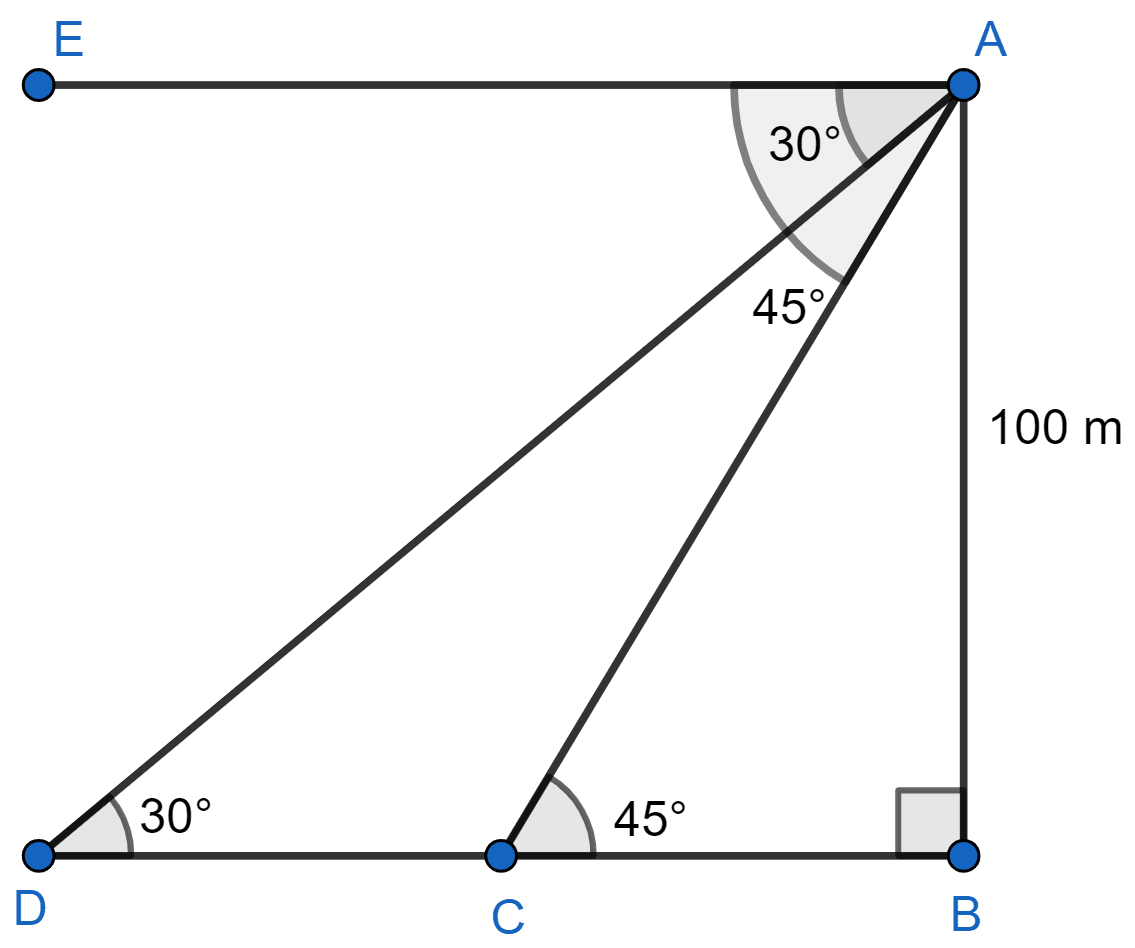
As observed from the top of a 100 m high light house, the angles of depression of two ships approaching it are 30° and 45°. If one ship is directly behind the other, find the distance between the two ships.

Let AB be the lighthouse and C and D be the position of ships.

From figure,

∠ADC = ∠EAD = 30° (Alternate angles are equal)

∠ACB = ∠EAC = 45° (Alternate angles are equal)

In right angle triangle ABD,

⇒ tan 30° = $\dfrac{\text{Perpendicular}}{\text{Base}}$

⇒ $\dfrac{1}{\sqrt{3}} = \dfrac{AB}{BD}$

⇒ BD = $\sqrt{3}AB = 100\sqrt{3}$ m.

In right angle triangle ABC,

⇒ tan 45° = $\dfrac{\text{Perpendicular}}{\text{Base}}$

⇒ $1 = \dfrac{AB}{BC}$

⇒ BC = AB = 100 m.

From figure,

CD = BD - BC = $100\sqrt{3} - 100 = 100(\sqrt{3} - 1)$

= 100 × (1.732 - 1) m.

= 100 × 0.732 = 73.2 m.

Hence, distance between two ships = 73.2 m.