Mathematics
If (2 cos 2A - 1)(tan 3A - 1) = 0; find all possible values of A.
Trigonometric Identities
13 Likes
Answer
Given,
⇒ (2 cos 2A - 1)(tan 3A - 1) = 0
⇒ 2 cos 2A - 1 = 0 or tan 3A - 1 = 0
⇒ 2 cos 2A = 1 or tan 3A = 1
⇒ cos 2A = or tan 3A = tan 45°
⇒ cos 2A = cos 60° or tan 3A = tan 45°
⇒ 2A = 60° or 3A = 45°
⇒ A = or A =
⇒ A = 30° or 15°.
Hence, A = 30° or 15°.
Answered By
7 Likes
Related Questions
If tan A = 1 and tan B = ; evaluate :
(i) cos A cos B - sin A sin B
(ii) sin A cos B + cos A sin B
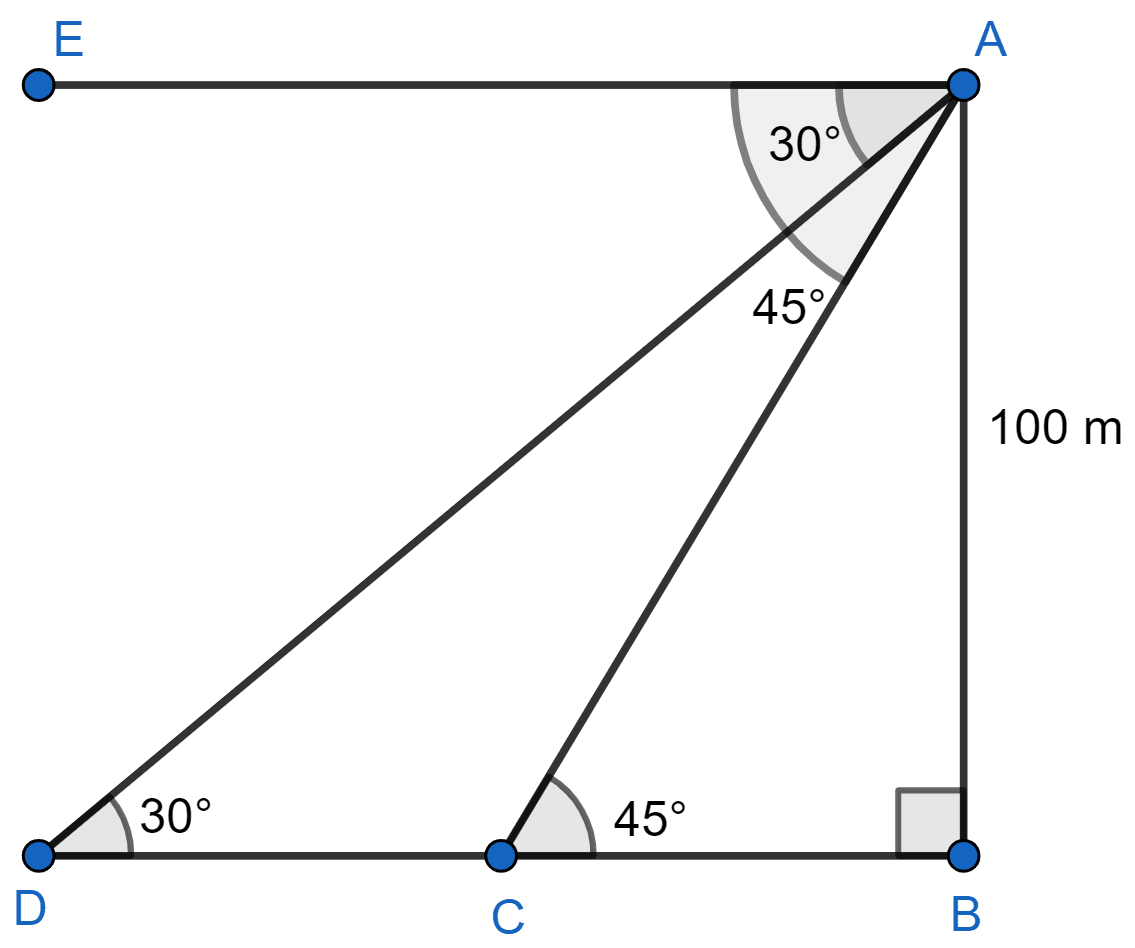
As observed from the top of a 100 m high light house, the angles of depression of two ships approaching it are 30° and 45°. If one ship is directly behind the other, find the distance between the two ships.
If cos A = ; find the value of .
From the top of a light house, it is observed that a ship is sailing directly towards it and the angle of depression of the ship changes from 30° to 45° in 10 minutes. Assuming that the ship is sailing with uniform speed; calculate in how much more time (in minutes) will the ship reach the light house ?