Mathematics
From the top of a light house, it is observed that a ship is sailing directly towards it and the angle of depression of the ship changes from 30° to 45° in 10 minutes. Assuming that the ship is sailing with uniform speed; calculate in how much more time (in minutes) will the ship reach the light house ?
Trigonometric Identities
38 Likes
Answer
Let AB be the lighthouse of height h meters and C and D be the position of the ship.
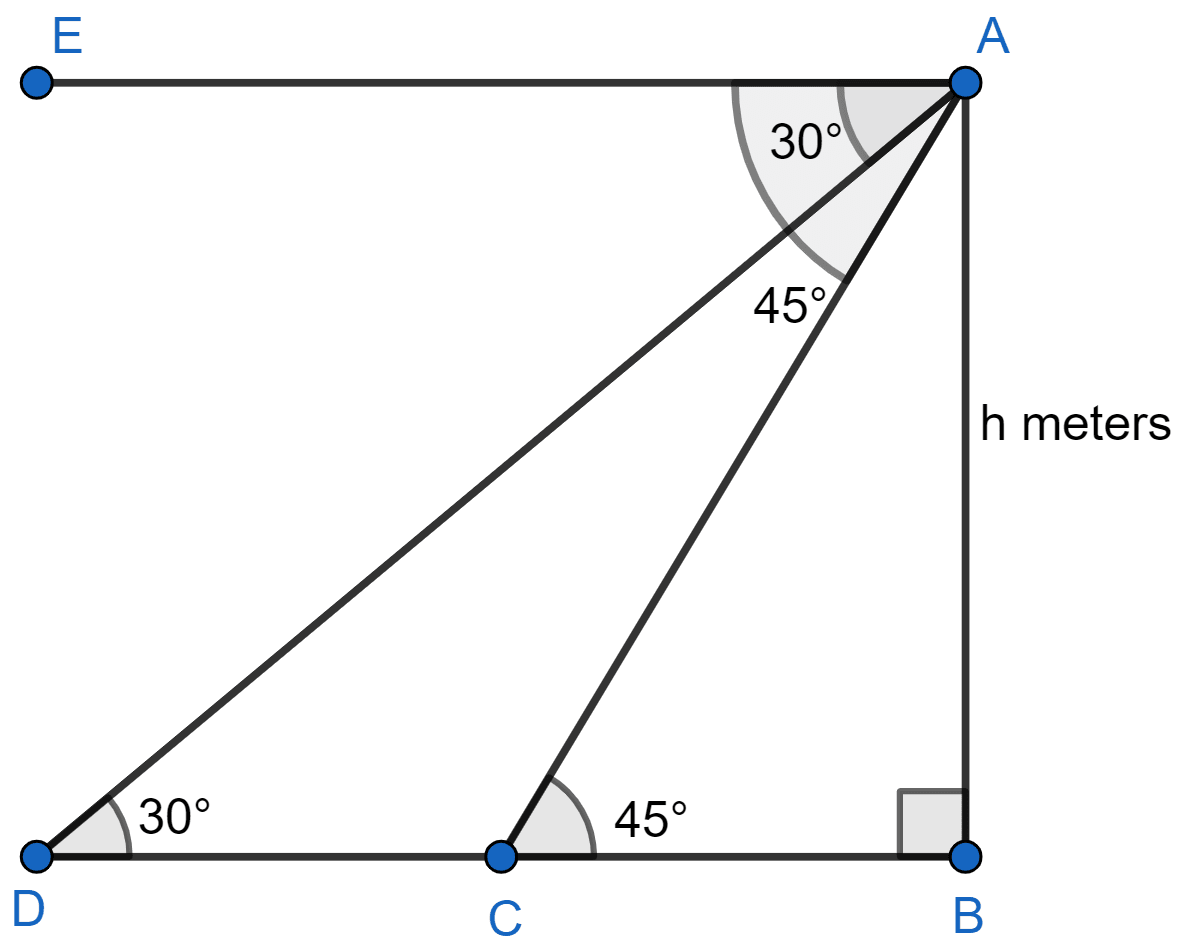
From figure,
∠ADC = ∠EAD = 30° (Alternate angles are equal)
∠ACB = ∠EAC = 45° (Alternate angles are equal)
From figure,
In right angle triangle ADB
⇒ tan 30° =
⇒
⇒ BD = .
In right angle triangle ABC
⇒ tan 45° =
⇒ 1 =
⇒ BC = AB = h.
From figure,
CD = BD - BC = meters.
Given,
Angle of depression of the ship changes from 30° to 45° in 10 minutes.
∴ Ship comes from position D to C in 10 minutes.
∴ Ship covers a distance of CD = in 10 minutes.
Speed of ship = meter/minute.
Time taken by ship to cover (BC = h meters) is
Hence, ship will reach the lighthouse in 13.66 minutes.
Answered By
12 Likes
Related Questions
If (2 cos 2A - 1)(tan 3A - 1) = 0; find all possible values of A.
If cos A = ; find the value of .
The angles of elevation of the top of a tower from two points on the ground at distances a and b meters from the base of the tower and in the same line are complementary. Prove that the height of the tower is meter.
A 20 m high vertical pole and a vertical tower are on the same level ground in such a way that the angle of elevation of the top of the tower, as seen from the foot of the pole, is 60° and the angle of elevation of the top of the pole, as seen from the foot of tower is 30°. Find :
(i) the height of the tower;
(ii) the horizontal distance between the pole and the tower.