Physics
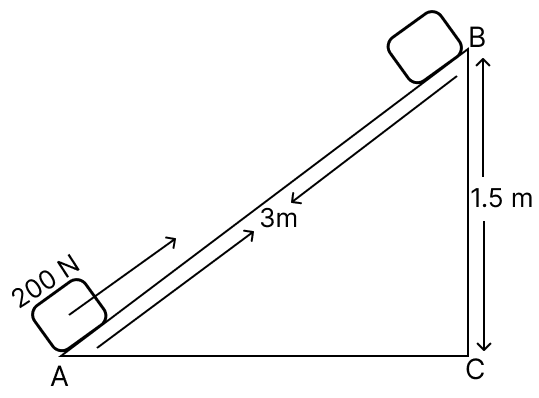
A block of mass 30 kg is pulled up a slope (diagram below) with a constant speed by applying a force of 200 N parallel to the slope. A and B are the initial and final positions of the block. Calculate the force of friction offered by the surface AB.
Force
4 Likes
Answer
Given, mass of block (m) = 30 kg
Force applied (F) = 200 N
Work done along AB :
WAB = F x SAB
= 200 x 3 = 600 N m = 600 J
Work done along CB:
WCB = m x g x SCB
= 30 x 10 x 1.5 = 450 J
Let, friction force = f
Work done by friction WF =f x 3
Hence, the force of friction offered by the surface AB is 50 N.
Answered By
2 Likes
Related Questions
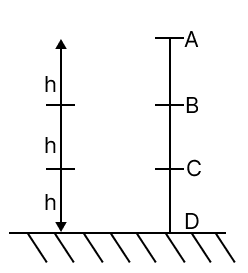
A ball of mass m is dropped freely from point A. It is given that AB = BC = CD = h. If the acceleration due to gravity at the given place is g, then what will be its
(a) potential energy at point A?
(b) kinetic energy at point C?
In a science exhibition, boys of a Secondary school made two types of periscopes. In one of the periscopes, ordinary glass was used as the reflecting material, while in the other, a prism was used. When Anushka put her eyes on the eyepiece of the periscope, she saw that the image formed in one of the periscopes was quite bright, while in the other, it was a little blurred.
(a) In which of the two periscopes, mirror or prism, Anushka saw the image brighter?
(b) Why is one of the images brighter than the other?
ABC is a glass block whose two sides, AB and BC, are at right angles to each other. A ray of light is incident on the surface AB, as shown in the diagram, and suffers total internal reflection before falling on the surface BC. Finally, the light ray emerges out along the surface BC.
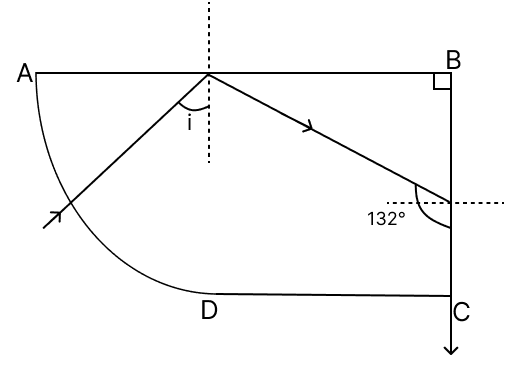
(a) What is the angle of incidence at the surface AB?
(b) What is the critical angle for the glass block BC?
(c) What would happen to the critical angle if the temperature of the glass block is increased?
A roller with a diameter of 0.2 m is raised over a pavement AB by applying forces F1 and F2, as shown in the diagram.
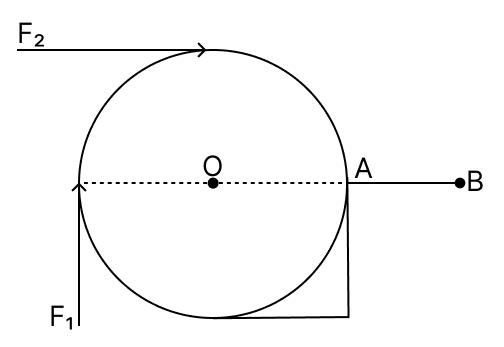
If the magnitude of both forces is 20 N, then compare the magnitudes of the torques produced by the two forces.