Mathematics
Calculate the area of quadrilateral ABCD, in which ∠ABD = 90°, triangle BCD is an equilateral triangle of side 24 cm and AD = 26 cm.
Mensuration
41 Likes
Answer
For Δ ABD,
By using the Pythagoras theorem,
Base2 + Height2 = Hypotenuse2
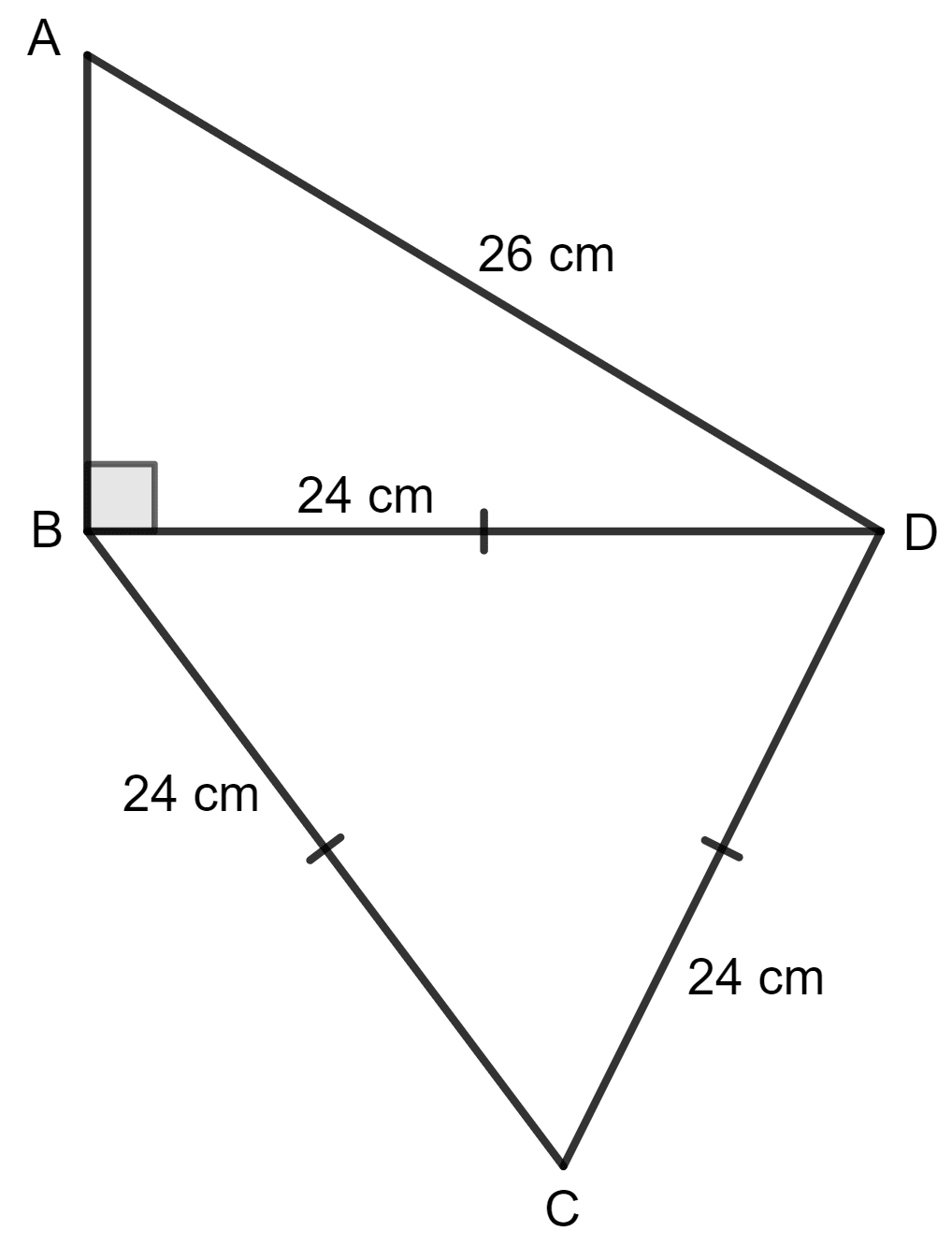
⇒ AB2 + BD2 = AD2
⇒ AB2 + (24)2 = (26)2
⇒ AB2 + 576 = 676
⇒ AB2 = 676 - 576
⇒ AB2 = 100
⇒ AB =
⇒ AB = 10 cm
Area of Δ ABD = x AB x BD
= x 10 x 24 cm2
= 5 x 24 cm2
= 120 cm2
Area of equilateral triangle BCD = x side2
= x 242
= x 576
= 144 cm2
= 249.41 cm2
Total area of quadrilateral ABCD = Δ ABD + Δ BCD
= 120 + 249.41 cm2
= 369.41 cm2
Hence, the area of quadrilateral ABCD is 369.41 cm2.
Answered By
17 Likes
Related Questions
Find the area of a quadrilateral one of whose diagonals is 30 cm long and the perpendiculars from the other two vertices are 19 cm and 11 cm respectively.
The diagonals of a quadrilateral are 16 cm and 13 cm. If they intersect each other at right angles; find the area of the quadrilateral.
Calculate the area of quadrilateral ABCD in which AB = 32 cm, AD = 24 cm, ∠A = 90° and BC = CD = 52 cm.
The perimeter of a rectangular field is km. If the length of the field is twice its width; find the area of the rectangle in sq. metres.