Mathematics
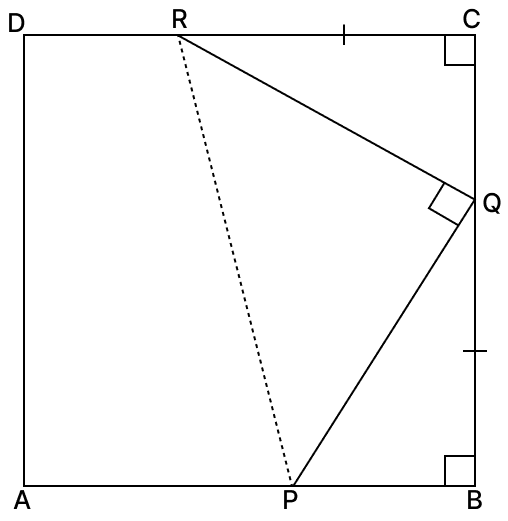
In the given figure, ABCD is a square and P, Q, R are points on AB, BC and CD respectively such that AP = BQ = CR and ∠PQR = 90°. Prove that:
(i) PB = QC
(ii) PQ = QR
(iii) ∠QPR = 45°
Triangles
2 Likes
Answer
(i) Given,
ABCD is a square.
AB = BC = CD = DA
Given,
AP = BQ = CR
From figure,
⇒ PB = AB - AP ….(1)
⇒ QC = BC - BQ
⇒ QC = AB - AP [As, BC = AB and BQ = AP] ….(2)
From eq.(1) and (2), we have :
⇒ PB = QC
Hence, proved that PB = QC.
(ii) In △PBQ and △QCR,
⇒ ∠PBQ = ∠QCR (Both equal to 90°)
⇒ BQ = CR (Given)
⇒ PB = QC (Proved above)
∴ △PBQ ≅ △QCR (By S.A.S axiom)
∴ PQ = QR (Corresponding parts of congruent triangles are equal)
Hence, proved that PQ = QR.
(iii) In △QPR,
⇒ PQ = QR
∴ △PQR is an isosceles triangle.
⇒ ∠QPR = ∠QRP = f (let) (Angles opposite to equal sides are equal)
By angle sum property of triangle,
⇒ ∠QPR + ∠QRP + ∠PQR = 180°
⇒ f + f + 90° = 180°
⇒ 2f = 180° - 90°
⇒ 2f = 90°
⇒ f =
⇒ f = 45°.
⇒ ∠QPR = ∠QRP = 45°.
Hence, proved that ∠QPR = 45°.
Answered By
1 Like
Related Questions
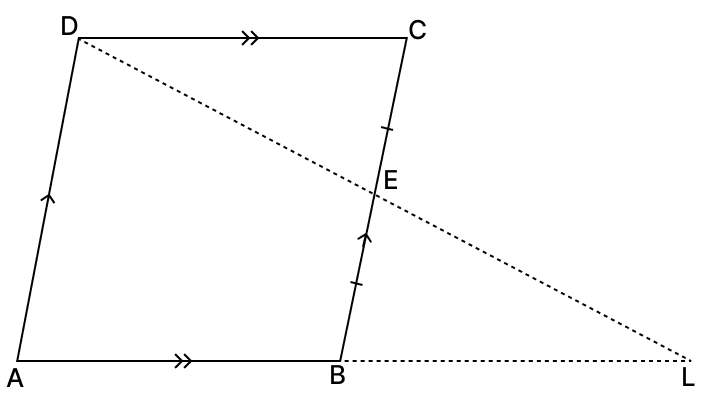
In the given figure, ABCD is a parallelogram, E is the mid-point of BC. DE produced meets AB produced at L. Prove that:
(i) AB = BL
(ii) AL = 2DC
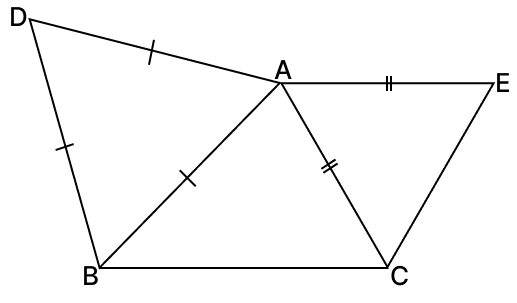
Equilateral triangle ABD and ACE are drawn on the sides AB and AC of △ABC as shown in the figure. Prove that :
(i) ∠DAC = ∠EAB
(ii) DC = BE
In the given figure, ABCD is a square, EF || BD and R is the mid-point of EF. Prove that:
(i) BE = DF
(ii) AR bisects ∠BAD
(iii) If AR is produced, it will pass through C.
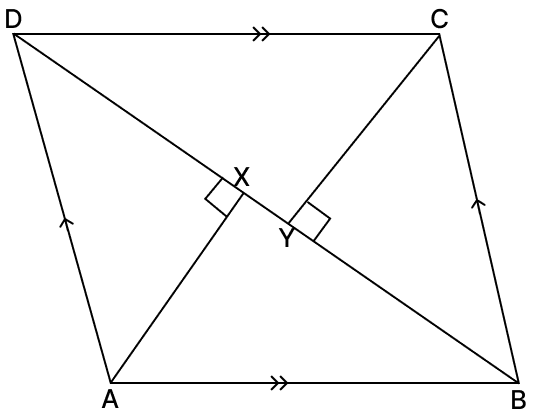
ABCD is a parallelogram in which ∠A and ∠C are obtuse. Points X and Y are taken on diagonal BD such that ∠AXD = ∠CYB = 90°. Prove that : XA = YC.