Mathematics
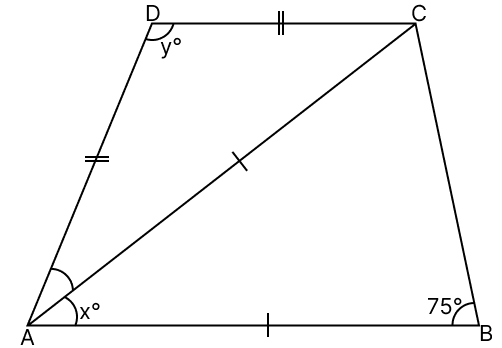
In the given figure, AC is the bisector of ∠A. If AB = AC, AD = CD and ∠ABC = 75°, find the values of x and y.
Triangles
1 Like
Answer
In △ABC,
AB = AC
⇒ ∠ABC = ∠ACB = 75° (Angles opposite to equal sides in a triangle are equal)
By angle sum property of triangle,
⇒ ∠ABC + ∠ACB + ∠BAC = 180°
⇒ 75° + 75° + x° = 180°
⇒ 150° + x° = 180°
⇒ x° = 180° - 150°
⇒ x° = 30°
⇒ x = 30.
Given,
AC is the bisector to ∠A
⇒ ∠DAC = ∠BAC = x° = 30°
In △ADC,
AD = CD
⇒ ∠DAC = ∠DCA = 30° (Angles opposite to equal sides are equal)
By angle sum property of triangle,
⇒ ∠DAC + ∠DCA + ∠ADC = 180°
⇒ 30° + 30° + y° = 180°
⇒ 60° + y° = 180°
⇒ y° = 180° - 60°
⇒ y° = 120°
⇒ y = 120.
Hence, the values of x = 30 and y = 120.
Answered By
1 Like
Related Questions
In the adjoining figure, AB = AC. If DB ⊥ BC and EC ⊥ BC, prove that :
(i) BD = CE
(ii) AD = AE
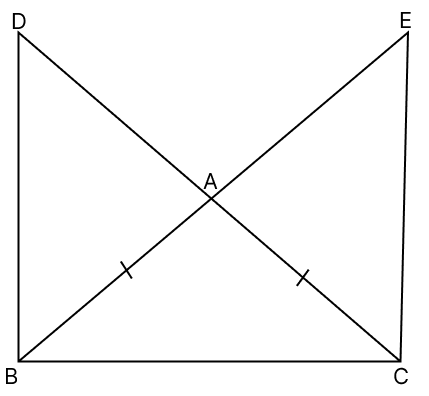
In the given figure, △ABC is an equilateral triangle and BC is produced to D such that BC = CD. Prove that AD ⊥ AB.
In a △PQR, ∠P = 50° and ∠R = 70°. Name :
(i) the shortest side
(ii) the longest side of the triangle
In a △LMN, if ∠M = 90°, name the longest side of the triangle.