Mathematics
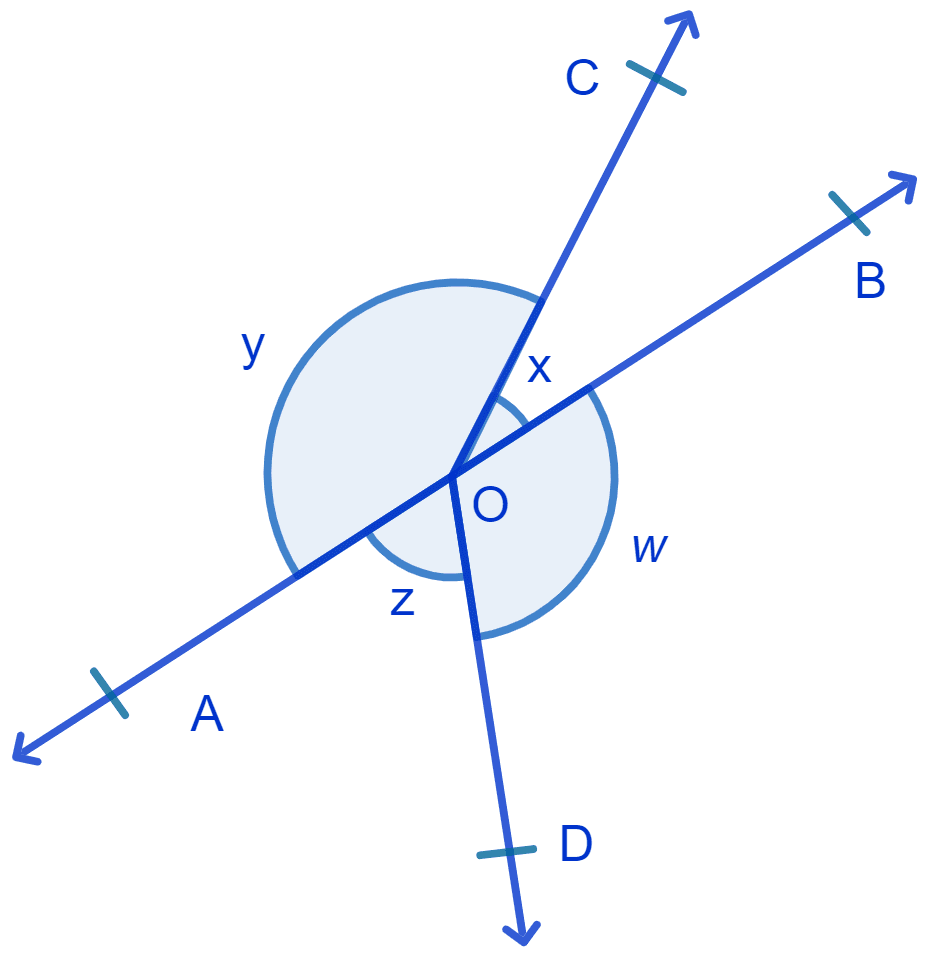
In Fig. if x + y = w + z, then prove that AOB is a line.
Lines & Angles
19 Likes
Answer
We know that,
Sum of all angles round a point is equal to 360°.
⇒ x + y + w + z = 360°
⇒ (x + y) + (w + z) = 360°
As,
x + y = w + z
⇒ (x + y) + (x + y) = 360°
⇒ 2(x + y) = 360°
⇒ (x + y) = = 180°.
⇒ x + y = 180° and w + z = 180°.
Since the sum of adjacent angles, x and y with OA and OB as the non-common arms is 180° we can say that AOB is a straight line.
Hence, proved that AOB is a straight line.
Answered By
6 Likes
Related Questions
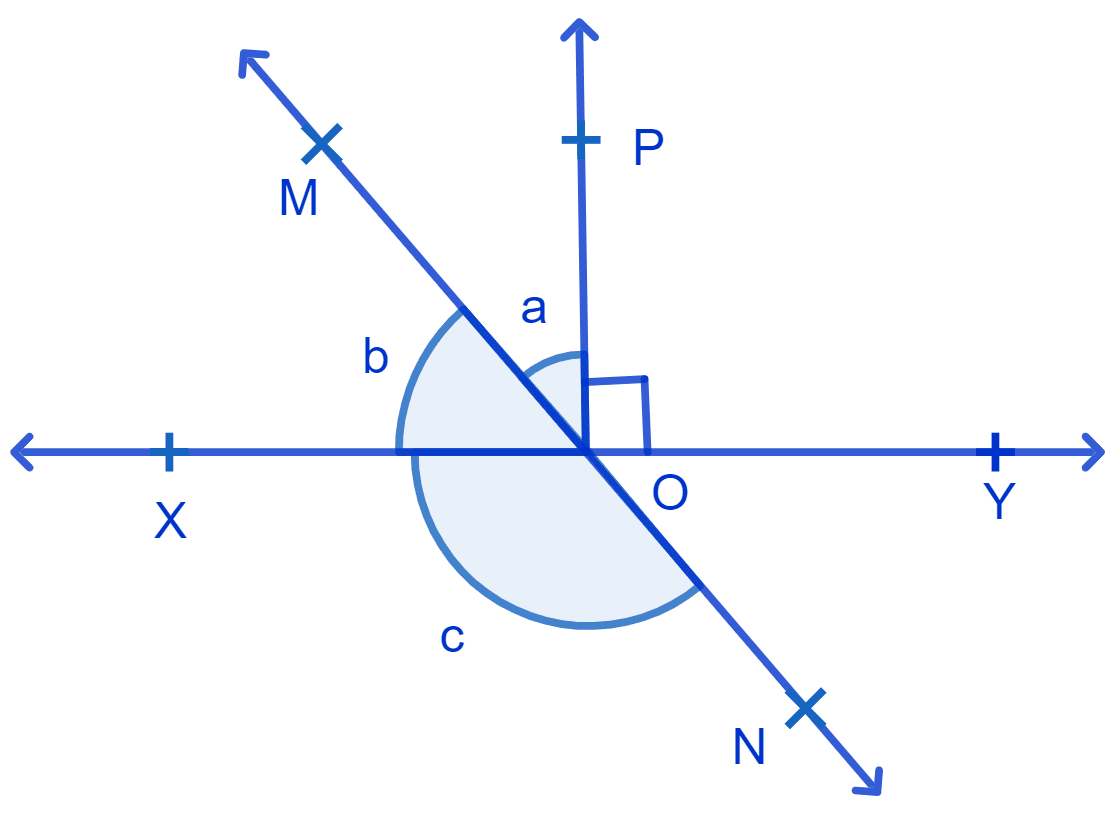
In Fig. lines XY and MN intersect at O. If ∠POY = 90° and a : b = 2 : 3, find c.
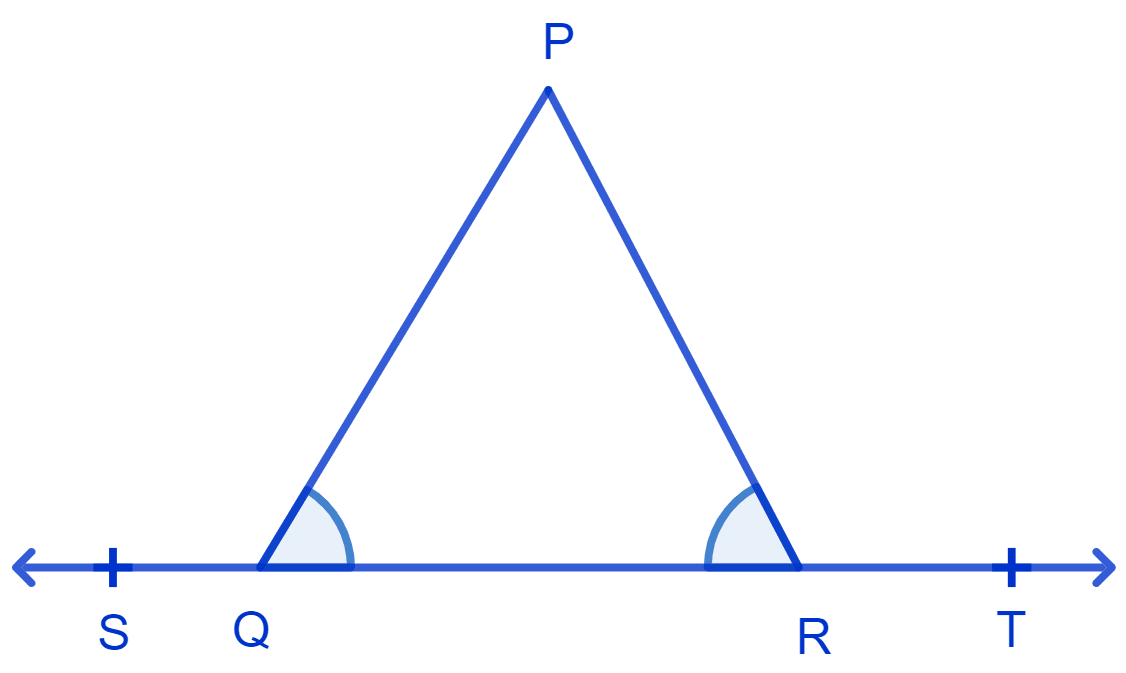
In Fig. ∠PQR = ∠PRQ, then prove that ∠PQS = ∠PRT.
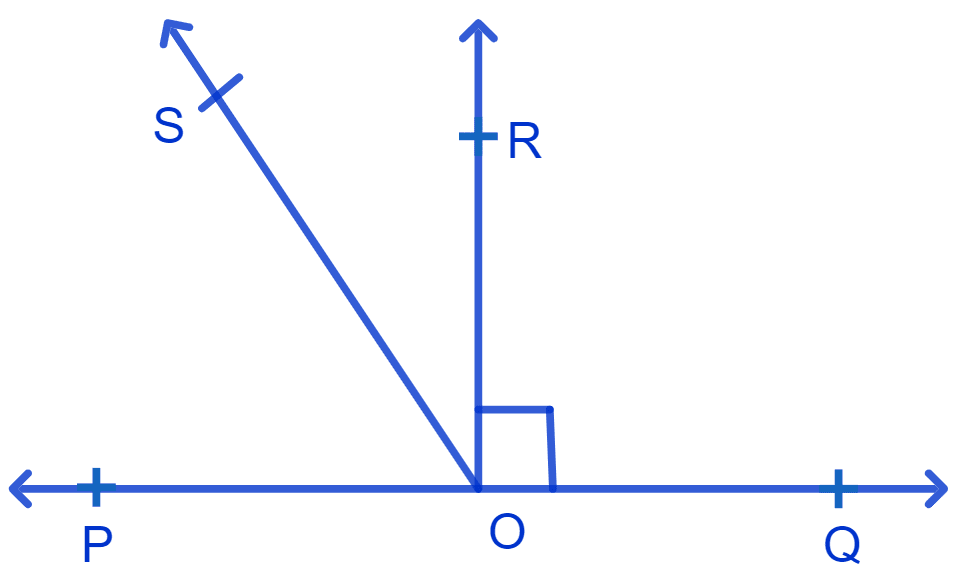
In Fig. POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that
∠ROS = (∠QOS – ∠POS).
It is given that ∠XYZ = 64° and XY is produced to point P. Draw a figure from the given information. If ray YQ bisects ∠ZYP, find ∠XYQ and reflex ∠QYP.