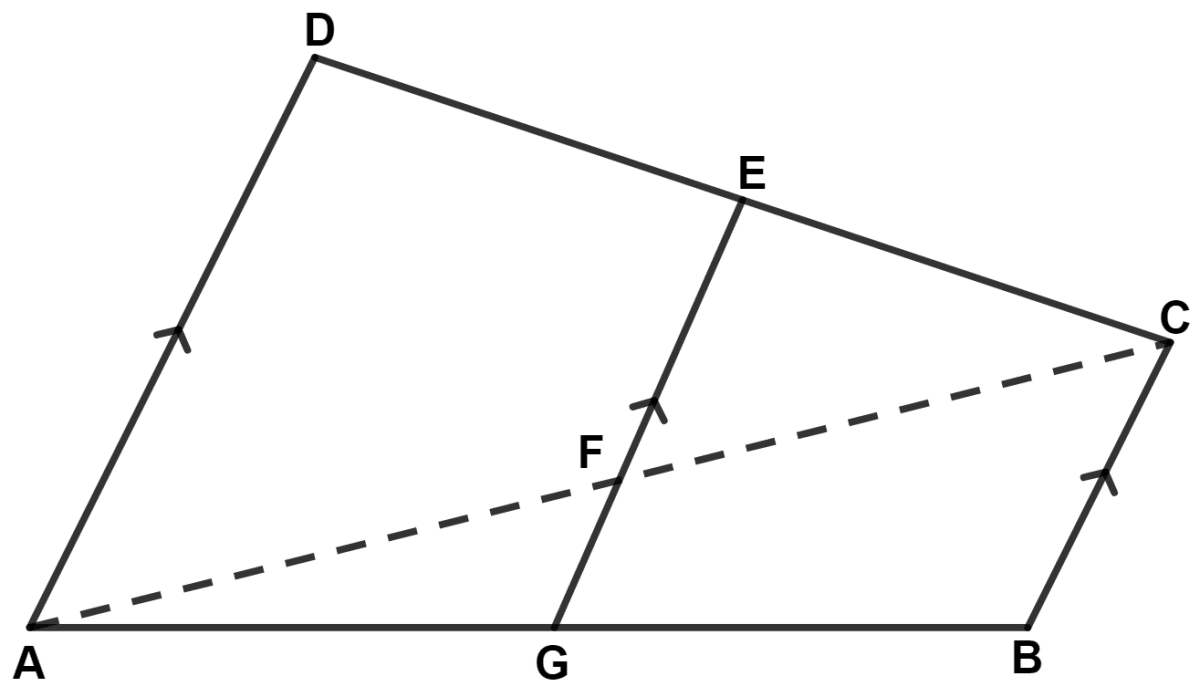
In the figure given below (not drawn to scale), AD ∥ GE ∥ BC, DE = 18 cm, EC = 3 cm, AD = 35 cm. Find :

(a) AF : FC

(b) length of EF

(c) area(trapezium ADEF) : area(Δ EFC)

(d) BC ∶ GF

(a) In △ ACD and △ FCE,

⇒ ∠ACD = ∠FCE (Common angles)

⇒ ∠ADC = ∠FEC (Corresponding angles are equal)

∴ △ ACD ~ △ FCE (By A.A. axiom)

We know that,

Ratio of corresponding sides of similar triangle are proportional.

$\therefore \dfrac{FC}{AC} = \dfrac{EC}{CD} \\[1em] \Rightarrow \dfrac{FC}{AC} = \dfrac{EC}{EC + ED} \\[1em] \Rightarrow \dfrac{FC}{AC} = \dfrac{3}{3 + 18} \\[1em] \Rightarrow \dfrac{FC}{AC} = \dfrac{3}{21} \\[1em] \Rightarrow \dfrac{FC}{AC} = \dfrac{1}{7}.$

Let FC = x and AC = 7x.

From figure,

AF = AC - FC = 7x - x = 6x.

$\therefore \dfrac{AF}{FC} = \dfrac{6x}{x} = \dfrac{6}{1}$ = 6 : 1.

Hence, AF : FC = 6 : 1.

(b) Since, △ ACD ~ △ FCE

$\therefore \dfrac{EF}{AD} = \dfrac{EC}{CD} \\[1em] \Rightarrow \dfrac{EF}{35} = \dfrac{3}{21} \\[1em] \Rightarrow EF = \dfrac{3}{21} \times 35 \\[1em] \Rightarrow EF = \dfrac{105}{21} = 5 \text{ cm}.$

Hence, EF = 5 cm.

(c) We know that,

The ratio of the area of two similar triangles is equal to the square of the ratio of any pair of the corresponding sides of the similar triangles.

$\therefore \dfrac{\text{Area of △ ADC}}{\text{Area of △ FCE}} = \Big(\dfrac{DC}{EC}\Big)^2 \\[1em] \Rightarrow \dfrac{\text{Area of △ ADC}}{\text{Area of △ FCE}} = \Big(\dfrac{21}{3}\Big)^2 \\[1em] \Rightarrow \dfrac{\text{Area of △ ADC}}{\text{Area of △ FCE}} = \dfrac{441}{9} \\[1em] \Rightarrow \dfrac{\text{Area of △ ADC}}{\text{Area of △ FCE}} = \dfrac{49}{1}.$

Let area of △ ADC = 49a and area of △ FCE = a.

Area of trapezium ADEF = Area of △ ADC - Area of △ FCE = 49a - a = 48a.

$\therefore \dfrac{\text{Area of trapezium ADEF}}{\text{Area of △ FCE}} = \dfrac{48a}{a} = \dfrac{48}{1}.$

Hence, area of trapezium ADEF : area of △ EFC = 48 : 1.

(d) In △ AGF and △ ABC,

⇒ ∠AGF = ∠ABC (Corresponding angles are equal)

⇒ ∠GAF = ∠BAC (Common angles)

∴ △ AGF ~ △ ABC (By A.A. axiom)

We know that,

Ratio of corresponding sides of similar triangle are proportional.

$\therefore \dfrac{AC}{AF} = \dfrac{BC}{GF}$

From part (a),

⇒ FC = x and AC = 7x

⇒ AF = AC - FC = 7x - x = 6x.

$\Rightarrow \dfrac{BC}{GF} = \dfrac{7x}{6x} = \dfrac{7}{6}.$

Hence, BC : GF = 7 : 6.