Mathematics
In right triangles ABC and DEF, if hypotenuse AB = EF and side AC = DE, then △ABC is congruent to:
△FED
△EFD
△DEF
△FDE
Triangles
3 Likes
Answer
In △ABC and △EFD,
⇒ AB = EF (Given)
⇒ AC = DE (Given)
⇒ ∠C = ∠D (Both equal to 90°)
∴ △ABC ≅ △EFD (By R.H.S axiom)
Hence, option 2 is the correct option.
Answered By
1 Like
Related Questions
In the adjoining figure, AB = AC, BD = CD, ∠BAD = 32°, ∠BDC = 56°, ∠CAD = 2x° and ∠BDA = (x + y)°. The values of x and y will be :
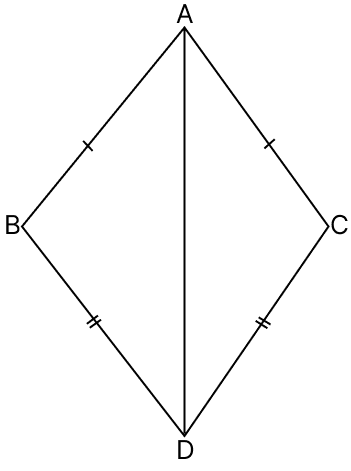
x = 10, y = 16
x = 16, y = 12
x = 18, y = 8
x = 12, y = 16
In the figure, AB = AC and DB = DC. ∠ABD : ∠ACD is :
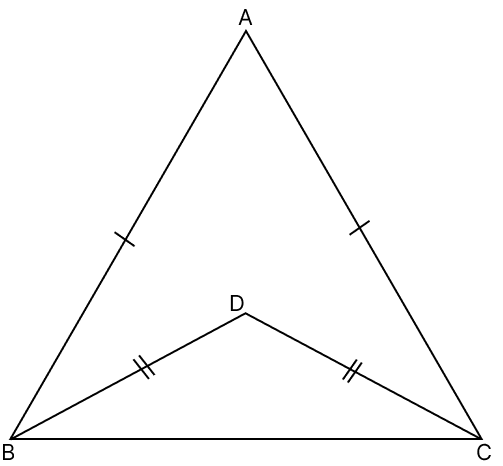
1 : 2
2 : 1
1 : 1
1 : 3
ABC is a right angled triangle whose hypotenuse is AC. If AB : BC = 3 : 4, then the smallest angle of the triangle is :
∠A
∠B
∠C
None of these
If a, b, c be the lengths of the sides of a triangle, then :
a = b + c
a < b + c
a > b + c
a < b - c