Mathematics
Study the graph and answer each of the following:
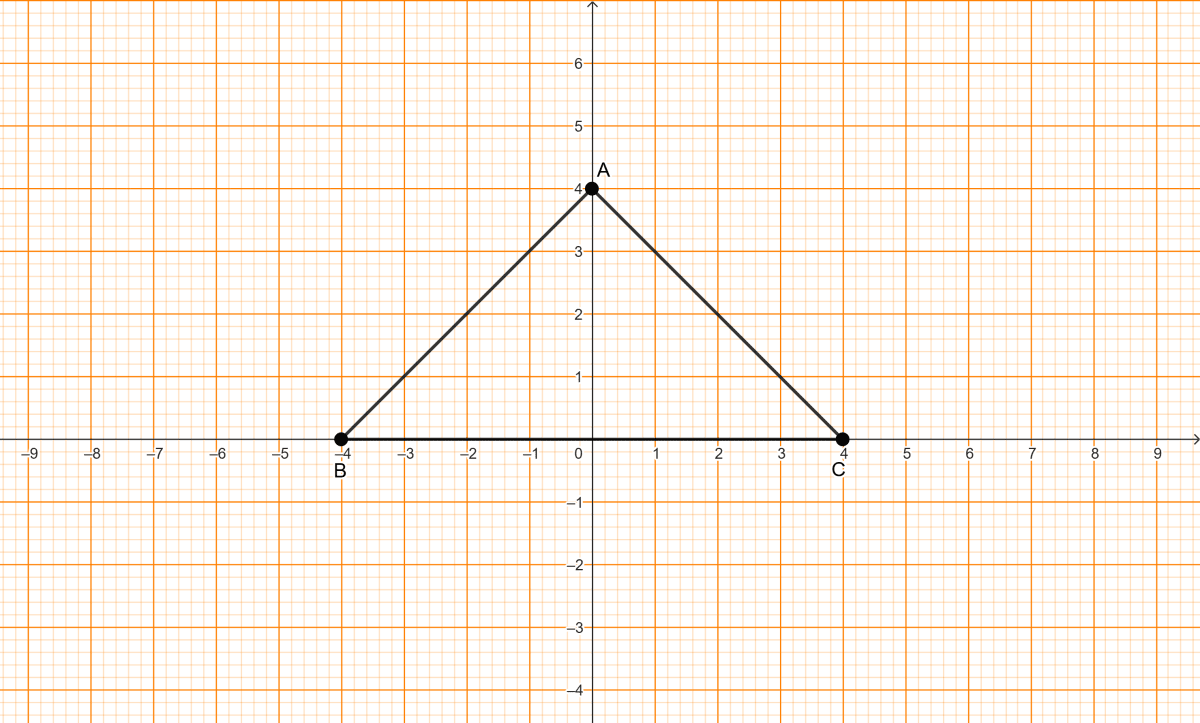
(i) Write down the co-ordinates of A, B and C. Reflect point A in x-axis and mark as A'.
(ii) Name the invariant point in 2nd quadrant on reflection in x-axis.
(iii) Join the points ABA'C. Name the figure formed.
Reflection
2 Likes
Answer
(i) A = (0, 4), B = (-4, 0) and C = (4, 0)
(ii) B
(iii) Square
Reason
From graph,
Co-ordinates of A = (0, 4), B = (-4, 0) and C = (4, 0).
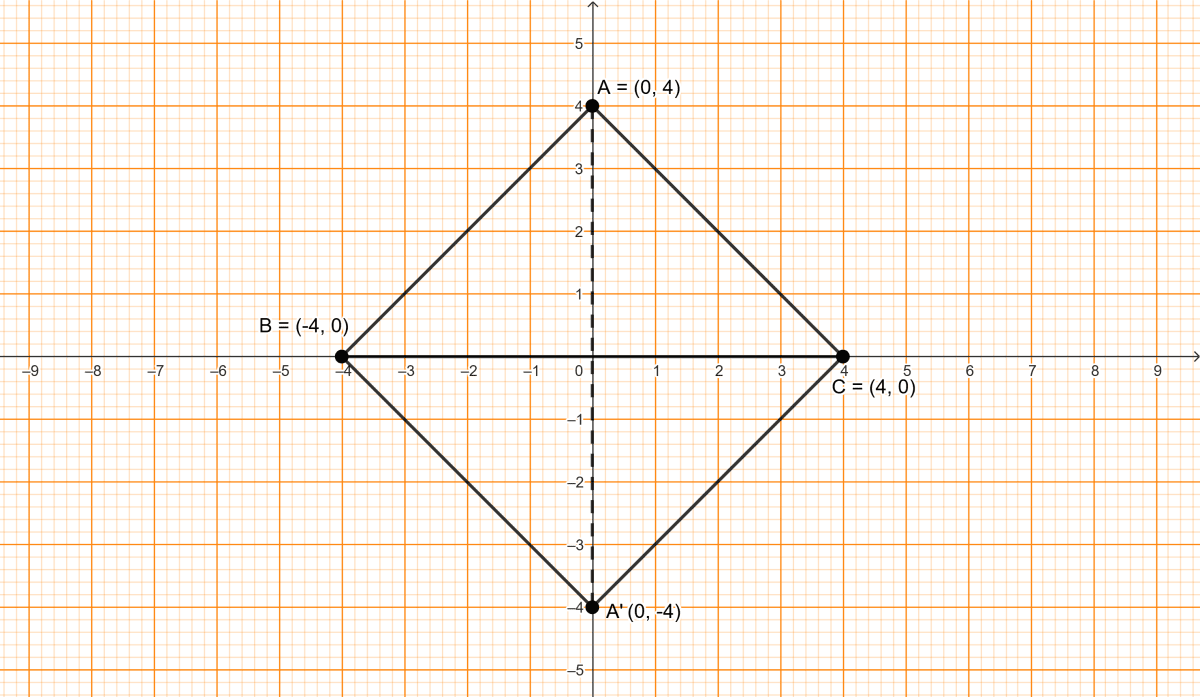
Since, point B is in 2nd quadrant and it lies on x-axis and on reflection in x-axis it remains there only. Thus, B is invariant.
By formula,
Slope =
Slope of AB = = 1
Slope of A'B = = -1.
Since, product of slope of AB and A'B is -1.
Thus, AB and A'B are perpendicular to each other. Since, all sides are equal and angle between sides = 90°.
∴ ABA'C is a square.
Answered By
3 Likes
Related Questions
Use graph sheet for this question.
(a) Plot A(0, 3), B(2, 1) and C(4, -1).
(b) Reflect point B and C in y-axis and name their images as B' and C' respectively. Plot and write coordinates of the points B' and C'.
(c) Reflect point A in the line BB' and name its images as A'.
(d) Plot and write coordinates of point A'.
(e) Join the points ABA'B' and give the geometrical name of the closed figure so formed.
Assertion (A) : The point (-2, 8) is invariant under reflection in line x = -2
Reason (R) : If a point has its x-coordinate 0, it is invariant under reflection in both axes.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
Both A and R are true.
(a) Point P(2, -3) on reflection becomes P'(2, 3). Name the line of reflection (say L1).
(b) Point P' is reflected to P'' along the line (𝐿2), which is perpendicular to the line 𝐿1 and passes through the point, which is invariant along both axes. Write the coordinates of P''.
(c) Name and write the coordinates of the point of intersection of the lines 𝐿1 and 𝐿2.
(d) Point P is reflected to P''' on reflection through the point named in the answer of part I of this question. Write the coordinates of P'''. Comment on the location of the points P'' and P'''.
ABC is a triangle as shown in the figure below.
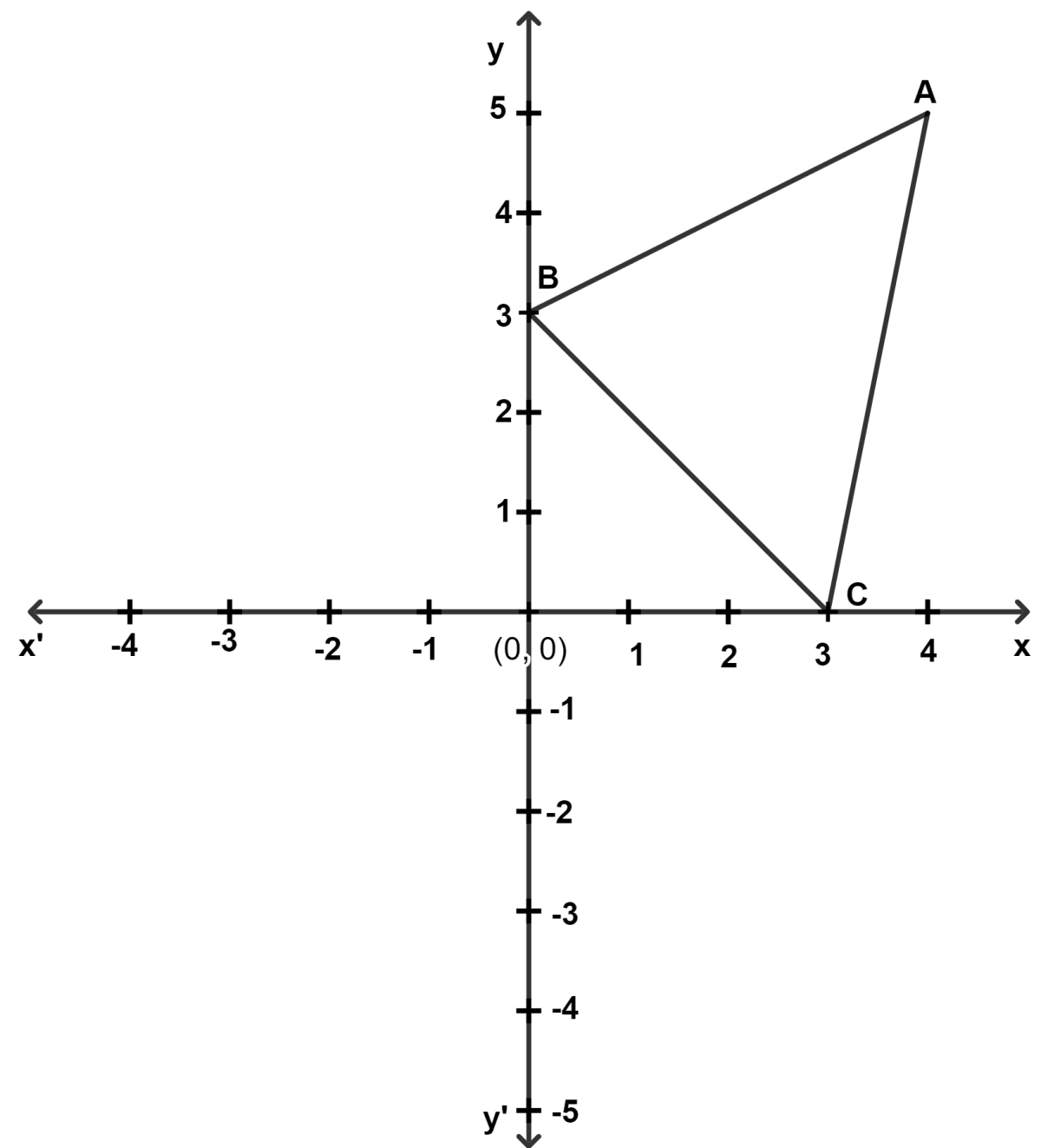
(a) Write down the coordinates of A, B and C on reflecting through the origin.
(b) Write down the coordinates of the point/s which remain invariant on reflecting the triangle ABC on the x-axis and y-axis respectively.