Mathematics
The daily wages of 80 workers in a project are given below.
| Wages (in ₹) | No. of workers |
|---|---|
| 400 - 450 | 2 |
| 450 - 500 | 6 |
| 500 - 550 | 12 |
| 550 - 600 | 18 |
| 600 - 650 | 24 |
| 650 - 700 | 13 |
| 700 - 750 | 5 |
Use a graph paper to draw an ogive for the above distribution. (Use a scale of 2 cm = ₹ 50 on x-axis and 2 cm = 10 workers on y-axis). Use your ogive to estimate :
(i) the median wages of the workers.
(ii) the lower quartile wage of workers.
(iii) the number of workers who earn more than ₹ 625 daily.
Measures of Central Tendency
19 Likes
Answer
Cumulative frequency distribution table :
| Wages (in ₹) | No. of workers | Cumulative frequency |
|---|---|---|
| 400 - 450 | 2 | 2 |
| 450 - 500 | 6 | 8 (2 + 6) |
| 500 - 550 | 12 | 20 (8 + 12) |
| 550 - 600 | 18 | 38 (20 + 18) |
| 600 - 650 | 24 | 62 (38 + 24) |
| 650 - 700 | 13 | 75 (62 + 13) |
| 700 - 750 | 5 | 80 (75 + 5) |
Here, n = 80, which is even.
Median = th term
= = 40th term.
(i) Steps of construction :
Take 2 cm = ₹ 50 on x-axis.
Take 1 cm = 10 workers on y-axis.
Plot the point (400, 0) as ogive starts on x-axis representing lower limit of first class.
Plot the points (450, 2), (500, 8), (550, 20), (600, 38), (650, 62), (700, 75) and (750, 80).
Join the points by a free-hand curve.
Draw a line parallel to x-axis from point I (no. of workers) = 40, touching the graph at point J. From point J draw a line parallel to y-axis touching x-axis at point K.
From graph, K = ₹ 605
Hence, median = ₹ 605.
(ii) Here, n = 80, which is even.
By formula,
Lower quartile = = 20th term.
Draw a line parallel to x-axis from point L (no. of workers) = 20, touching the graph at point Q. From point Q draw a line parallel to y-axis touching x-axis at point M.
From graph, M = ₹ 550
Hence, lower quartile = ₹ 550.
(iii) Draw a line parallel to y-axis from point N (wages) = ₹ 625, touching the graph at point O. From point O draw a line parallel to x-axis touching y-axis at point P.
From graph, P = 50.
∴ 50 workers earns either less or equal to ₹ 625.
Workers earning more than ₹ 625 = 80 - 50 = 30.
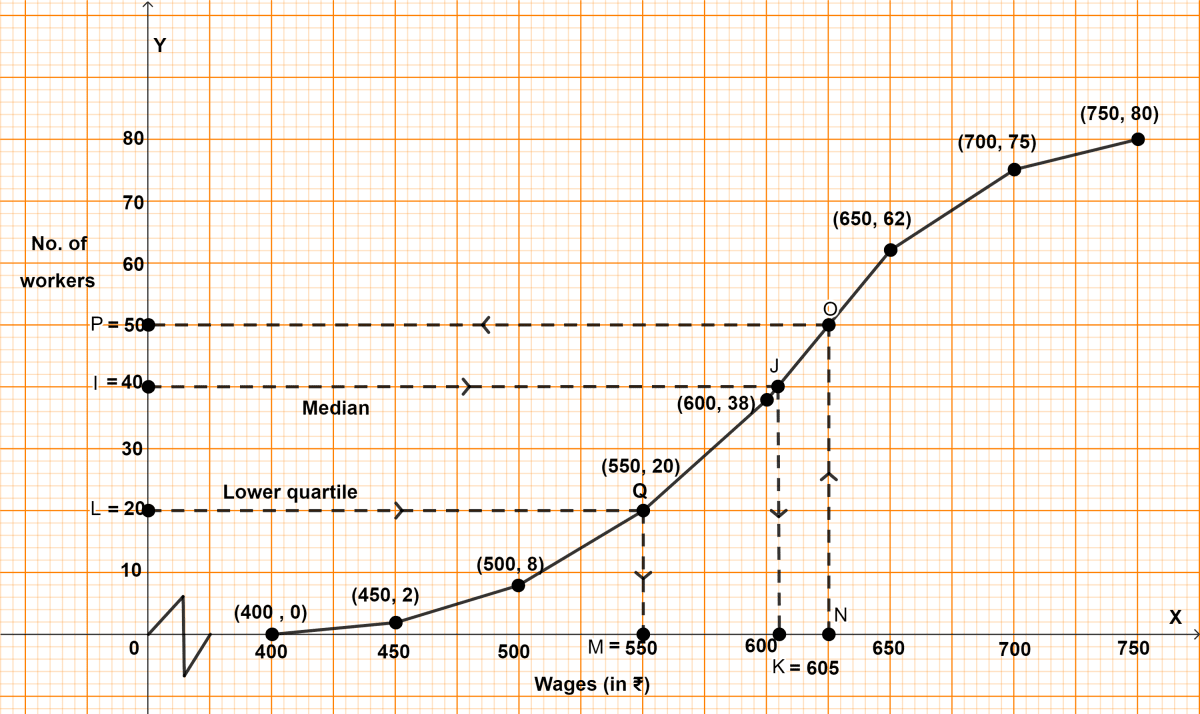
Hence, no. of workers earning more than ₹ 625 = 30.
Answered By
10 Likes
Related Questions
The monthly income of a group of 320 employees in a company is given below :
Monthly income No. of employees 6 - 7 20 7 - 8 45 8 - 9 65 9 - 10 95 10 - 11 60 11 - 12 30 12 - 13 5 Draw an ogive of the given distribution on a graph sheet taking 2 cm = ₹ 1000 on one axis and 2 cm = 50 employees on the other axis. From the graph determine :
(i) the median wage.
(ii) the number of employees whose income is below ₹ 8500.
The mean of numbers 45, 52, 60, x, 69, 70, 26, 81 and 94 is 68. Find the value of x. Hence, estimate the median for the resulting data.
The marks of 10 students of a class in an examination arranged in ascending order is as follows :
13, 35, 43, 46, x, x + 4, 55, 61, 71, 80.
If the median marks is 48, find the value of x. Hence, find the mode of the given data.
The histogram below represents the scores obtained by 25 students in a Mathematics mental test. Use the data to :
(i) Frame a frequency distribution table.
(ii) To calculate mean.
(iii) To determine the modal class.
