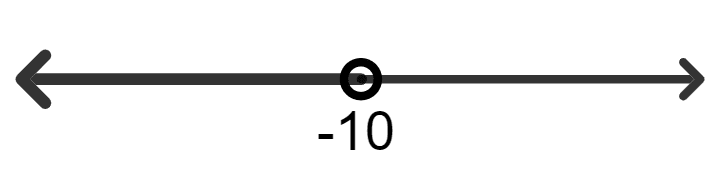If 11 + 2x > 5 and x ∈ {negative integers}, then the set to which x belongs is:
{-2, -1}
{-3, -2, -1, ...............}
{-3, -2, -1}
{1, 2, 3}
Answer
11 + 2x > 5
⇒ 2x > 5 - 11
⇒ 2x > - 6
⇒ x > -
⇒ x > - 3
∵ x is a negative integer.
∵ Solution set = {-2 , - 1}
Hence, option 1 is the correct option.
If 3x + 1 ≤ 16 and x ∈ {real numbers}, then the values of x represented on a number line are:
1.

2.

3.

4.

Answer
3x + 1 ≤ 16
⇒ 3x ≤ 16 - 1
⇒ 3x ≤ 15
⇒ x ≤
⇒ x ≤ 5
∵ x is a real number.
∵ Solution set = {........,- 3, -2 , - 1, 0, 1, 2, 3, 4, 5}

Hence, option 3 is the correct option.
If 3 - 2x ≥ x - 10, x ∈ W, the solution set is:
{1, 2, 3, 4, ...............}
{1, 2, 3, 4, 5}
{o, 1, 2, 3, 4}
{1, 2, 3, 4}
Answer
3 - 2x ≥ x - 10
⇒ 3 + 10 ≥ x + 2x
⇒ 13 ≥ 3x
⇒ ≥ x
⇒ 4.33.... ≥ x
∵ x is a whole number.
∵ Solution set = {0, 1, 2, 3, 4}
Hence, option 3 is the correct option.
If x ∈ W and ≥ 4, the solution set is:
{0, 1, 2, 3, 4, 5}
{0, 1, 2, 3, 4, 5, 6}
{7, 8, 9, 10, ...............}
{7, 8, 9, 10}
Answer
≥ 4
On cross multiplying, we get
⇒ (2x - 1) ≥ 4 3
⇒ 2x - 1 ≥ 12
⇒ 2x ≥ 12 + 1
⇒ 2x ≥ 13
⇒ x ≥
⇒ x ≥ 6.5
∵ x is a whole number.
∵ Solution set = {7, 8, 9, 10......}
Hence, option 3 is the correct option.
If x is an integer and -2(x + 3) > 5; the solution set on the number line is:
1.

2.

3.
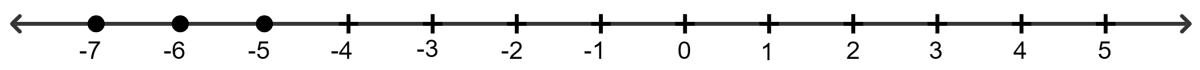
4.
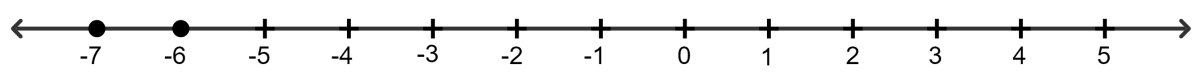
Answer
-2(x + 3) > 5
⇒ -2x - 6 > 5
⇒ -2x > 5 + 6
⇒ -2x > 11
⇒ x > -
⇒ x > - 5.5
∵ x is a whole number.
∵ Solution set = {- 8 ,- 7, - 6,......}
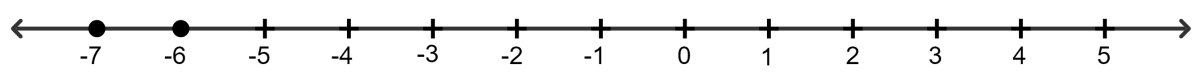
Hence, option 4 is the correct option.
Solve : 7 > 3x - 8 ; x ∈ N.
Answer
7 > 3x - 8
⇒ 7 + 8 > 3x
⇒ 15 > 3x
⇒ x <
⇒ x < 5
∵ x is a natural number.
Hence, solution set = {1, 2, 3, 4}.
Solve : - 17 < 9y - 8 ; y ∈ Z.
Answer
- 17 < 9y - 8
⇒ - 17 + 8 < 9y
⇒ - 9 < 9y
⇒ y > -
⇒ y > - 1
∵ x is a integer.
Hence, solution set = {0, 1, 2, 3, 4,.........}.
Solve : x + 8 < 12 ; x ∈ W.
Answer
x + 8 < 12
⇒ x < 12 - 8
⇒ x < 4
⇒ x <
⇒ x <
⇒ x < 6
∵ x is a whole number.
Hence, solution set = {0, 1, 2, 3, 4, 5}.
Solve the inequation 8 - 2x ≥ x - 5; x ∈ N.
Answer
8 - 2x ≥ x - 5
⇒ 8 + 5 ≥ x + 2x
⇒ 13 ≥ 3x
⇒ ≥ x
⇒ 4.33... ≥ x
∵ x is a natural number.
Hence, solution set = {1, 2, 3, 4}.
Solve the inequality 18 - 3 (2x - 5) > 12 ; x ∈ W.
Answer
18 - 3 (2x - 5) > 12
⇒ 18 - 6x + 15 > 12
⇒ 33 - 6x > 12
⇒ - 6x > 12 - 33
⇒ - 6x > - 21
⇒ 6x < 21
⇒ x <
⇒ x < 3.5
∵ x is a whole number.
Hence, solution set = {0, 1, 2, 3}.
Solve : 4x - 5 > 10 - x, x ∈ {0, 1, 2, 3, 4, 5, 6, 7}.
Answer
4x - 5 > 10 - x
⇒ 4x + x > 10 + 5
⇒ 5x > 15
⇒ x >
⇒ x > 3
∵ x is a whole number.
Hence, solution set = {4, 5, 6, 7}.
Solve : 15 - 2(2x - 1) < 15, x ∈ Z.
Answer
15 - 2(2x - 1) < 15
⇒ 15 - 4x + 2 < 15
⇒ 17 - 4x < 15
⇒ - 4x < 15 - 17
⇒ - 4x < - 2
⇒ 4x > 2
⇒ x >
⇒ x > 0.5
∵ x is a whole number.
Hence, solution set = {1, 2, 3, 4,......}.
Solve : , x ∈ W.
Answer
By cross multiplying, we get
⇒ 2(2x + 3) > 5(4x - 1)
⇒ 4x + 6 > 20x - 5
⇒ 5 + 6 > 20x - 4x
⇒ 11 > 16x
⇒ > x
⇒ 0.6875 > x
∵ x is a whole number.
Hence, solution set = {0}.
Solve : 5x + 4 > 8x - 11; x ∈ Z
Answer
5x + 4 > 8x - 11
⇒ 11 + 4 > 8x - 5x
⇒ 15 > 3x
⇒ > x
⇒ 5 > x
⇒ x < 5
∵ x is a integer.
Hence, solution set = {......, -2, -1, 0, 1, 2, 3, 4}.

Solve : + 1 < - 3; x ∈ R
Answer
+ 1 < - 3
⇒ < - 3 - 1
⇒ < - 4
By cross multiplying, we get
⇒ x < -
⇒ x < -
⇒ x < - 10
∵ x is a real number.
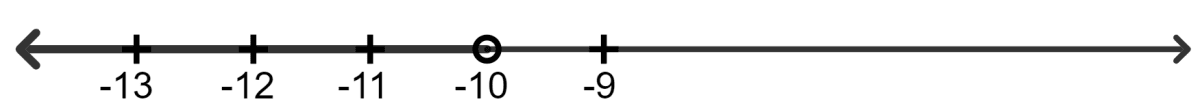
Solve :
Answer
⇒
Since L.C.M. of denominator 2 and 4 = 4, multiply each term with 4 to get:
⇒
⇒ 2x - 3x > - 4
⇒ - 1x > - 4
⇒ x < 4
∵ x is a natural number.
Hence, solution set = {1, 2, 3}.

Solve :
Answer
⇒
⇒
since L.C.M. of denominator 3 and 2 = 6, multiply each term with 6 to get:
⇒
⇒ 2 2x - 1 3x ≤ 6
⇒ 4x - 3x ≤ 6
⇒ x ≤ 6
∵ x is a whole number.
Hence, solution set = {0, 1, 2, 3, 4, 5, 6}.

Solve the inequation 5(x - 2) > 4(x + 3) - 24 and represent its solution on a number line. Given the replacement set is {-4, -3, -2, -1, 0, 1, 2, 3, 4}.
Answer
5(x - 2) > 4(x + 3) - 24
⇒ 5x - 10 > 4x + 12 - 24
⇒ 5x - 10 > 4x - 12
⇒ 5x - 4x > 10 - 12
⇒ x > - 2
∵ The replacement set is {-4, -3, -2, -1, 0, 1, 2, 3, 4}.
Hence, solution set = {-1, 0, 1, 2, 3, 4}.

Solve and represent its solution on a number line. Given the replacement set is {-8, -6, -4, 3, 6, 8, 12}.
Answer
⇒
⇒
⇒
⇒
By cross multiplying, we get
⇒ 2x - 2 < 6 3
⇒ 2x - 2 < 18
⇒ 2x < 18 + 2
⇒ 2x < 20
⇒ x <
⇒ x < 10
∵ The replacement set is {-8, -6, -4, 3, 6, 8, 12}.
Hence, solution set = {-8, -6, -4, 3, 6, 8}.

If x is a whole number and 12 - x > 3x - 5; the solution set is:
{1, 2, 3, 4}
{1, 2, 3, 4, 5}
{0, 1, 2, 3, 4, 5}
{0, 1, 2, 3, 4,}
Answer
12 - x > 3x - 5
⇒ 12 + 5 > 3x + x
⇒ 17 > 4x
⇒ x <
⇒ x < 4.25
∵ x is a whole number.
∵ Solution set = {0, 1, 2, 3, 4}
Hence, option 4 is the correct option.
If 5x - 3 ≤ 12 and x ∈ {-5, -3, -1, 1, 3, 5, 7} the solution set is:
{-5, -3, -1, 1, 3}
{-5, -3, -1}
{-5, -3, -1, 1}
{-3, -1, 1, 3, 6}
Answer
5x - 3 ≤ 12
⇒ 5x ≤ 12 + 3
⇒ 5x ≤ 15
⇒ x ≤
⇒ x ≤ 3
∵ As x ∈ {-5, -3, -1, 1, 3, 5, 7}.
∵ Solution set = {-5, -3, -1, 1, 3}
Hence, option 1 is the correct option.
If x ∈ {-7, -4, -1, 2, 5} and 25 - 3(2x -5) < 19; the solution set is:
{-7, -4, -1, 2}
{2, 5}
{0, 1, 2, 3}
{5}
Answer
25 - 3(2x - 5) < 19
⇒ 25 - 6x + 15 < 19
⇒ 40 - 6x < 19
⇒ - 6x < 19 - 40
⇒ - 6x < - 21
⇒ 6x > 21
⇒ x >
⇒ x > 3.5
∵ As x ∈ {-7, -4, -1, 2, 5}.
∵ Solution set = {5}
Hence, option 4 is the correct option.
If x is an integer and -4 < x ≤ 0, its solution set on the number line is:
1.

2.

3.

4.

Answer
-4 < x ≤ 0
∵ Solution set = {-4, -3, -2, -1, 0}
Hence, option 2 is the correct option.

If x is an integer and 7 - 4x < 15, the solution set on the number line is:
1.
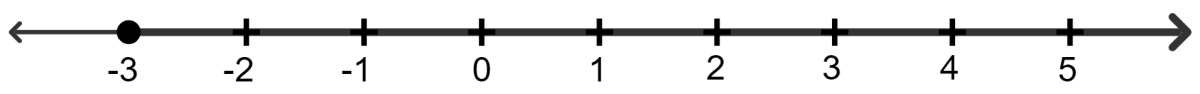
2.
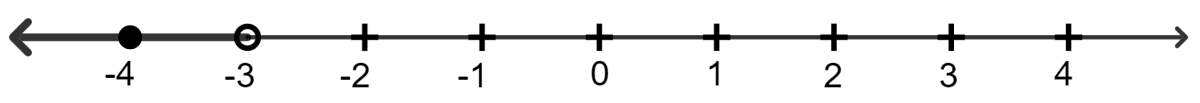
3.

4.

Answer
7 - 4x < 15
⇒ - 4x < 15 - 7
⇒ - 4x < 8
⇒ x < -
⇒ x < - 2
∵ As x is a integer.
∵ Solution set = {-1, 0, 1, 2, 3,.....}
Hence, option 3 is the correct option.

Statement 1: A set from which the values of the variable involved in the inequation are chosen is called the solution set.
Statement 2: A linear inequation variable (or unknown) has exactly one solution.
Which of the following options is correct?
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Answer
The solution set is the set of all values that satisfy the given inequation.
The set from which the values of the variable are chosen is called the replacement set, not the solution set.
So, statement 1 is false.
A linear inequation can have multiple solutions, not just one.
For example, x > 3 has infinite solutions
So, statement 2 is false.
∴ Both the statements are false.
Hence, option 2 is the correct option.
Assertion (A) : The solution set for :
x + 5 ≤ 10, if the replacement set is {x | x ≤ 5, x ∈ W} is {0, 1, 2, 3, 4, 5}.
Reason (R) : The set of elements of the replacement which satisfy the given inequation is called the solution set.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
We know that,
The set of elements of the replacement which satisfy the given inequation is called the solution set.
So, reason (R) is true.
Given,
⇒ x + 5 ≤ 10
⇒ x + 5 - 5 ≤ 10 - 5
⇒ x ≤ 5
Given,
The replacement set is {x | x ≤ 5, x ∈ W}.
∴ The solution set = {0, 1, 2, 3, 4, 5}
So, assertion (A) is true.
∴ Both A and R are correct, and R is the correct explanation for A.
Hence, option 1 is the correct option.
Assertion (A) : The solution set for :
x + 3 ≥ 15 is Φ, if the replacement set is {x | x < 10, x ∈ N}.
Reason (R) : If we change over the sides of an equality, we must change the sign from < to > or > to < or ≥ to ≤ or ≤ to ≥.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
Given,
⇒ x + 3 ≥ 15
Subtracting by 3 on both sides, we get :
⇒ x + 3 - 3 ≥ 15 - 3
⇒ x ≥ 12
The replacement set = {x | x < 10, x ∈ N} = {1, 2, 3, 4, 5, 6, 7, 8, 9}
Since no elements of the replacement set satisfy the inequality,
∴ Solution set is Φ.
So, assertion (A) is true.
Let's suppose a and b are two real numbers, such that :
⇒ a < b
⇒ b > a
Thus, we can say that, if we change over the sides of an equality, we must change the sign from < to > or > to < or ≥ to ≤ or ≤ to ≥.
So, reason (R) is true.
∴ Both A and R are correct, and R is not the correct explanation for A.
Hence, option 2 is the correct option.
Assertion (A) : x < -2 and x ≥ 1.
⇒ Solution set S = {x | -2 < x ≤ 1, x ∈ R}
Reason (R) : Two inequations can be written in a combined expression.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
Given, x < -2 and x ≥ 1
Means, x is less than -2 and x is greater than or equal to 1.
There is no real number that can satisfy both conditions at the same time.
So, assertion (A) is false.
In mathematics, it's common to combine multiple inequalities into a single expression using logical connectors.
For example, x > 3 and x ≤ 5 can be combined as 3 < x ≤ 5.
So, reason (R) is true.
∴ A is false, but R is true.
Hence, option 4 is the correct option.
Assertion (A) : The solution set in the system of negative integers for : 0 > -4 - p is {-3, -2. -1}.
Reason (R) : If the same quantity is subtracted from both sides of an equation, the symbol of inequality is reversed.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
Given,
⇒ 0 > -4 - p
Adding 4 on both sides, we get :
⇒ 0 + 4 > -4 - p + 4
⇒ 4 > -p
⇒ -p < 4
⇒ p > -4 (Multiplying by a negative number reverses the inequality)
This inequality means p can be any real number greater than -4.
The solution set = {-3, -2, -1}.
So, assertion (A) is true.
As we know that adding or subtracting the same quantity from both sides of an inequality does not change the direction of the inequality symbol.
So, reason (R) is false.
∴ A is true, but R is false.
Hence, option 3 is the correct option.
If the replacement set is the set of natural numbers, solve:
(i) x - 5 < 0
(ii) x + 1 ≤ 7
(iii) 3x - 4 > 6
(iv) 4x + 1 ≥ 17
Answer
(i) x - 5 < 0
⇒ x < 0 + 5
⇒ x < 5
∵ As x is a natural numbers.
Hence, solution set = {1, 2, 3, 4}.
(ii) x + 1 ≤ 7
⇒ x ≤ 7 - 1
⇒ x ≤ 6
∵ As x is a natural numbers.
Hence, solution set = {1, 2, 3, 4, 5, 6}.
(iii) 3x - 4 > 6
⇒ 3x > 6 + 4
⇒ 3x > 10
⇒ x >
⇒ x > 3.33.....
∵ As x is a natural numbers.
Hence, solution set = {4, 5, 6,.......}.
(iv) 4x + 1 ≥ 17
⇒ 4x ≥ 17 - 1
⇒ 4x ≥ 16
⇒ x ≥
⇒ x ≥ 4
∵ As x is a natural numbers.
Hence, solution set = {4, 5, 6,.......}.
If the replacement set = {-6, -3, 0, 3, 6, 9}, find the truth set of the following:
(i) 2x - 1 > 9
(ii) 3x + 7 ≤ 1
Answer
(i) 2x - 1 > 9
⇒ 2x > 9 + 1
⇒ 2x > 10
⇒ x >
⇒ x > 5
∵ As the replacement set = {-6, -3, 0, 3, 6, 9}.
Hence, solution set = {6, 9}.
(ii) 3x + 7 ≤ 1
⇒ 3x ≤ 1 - 7
⇒ 3x ≤ - 6
⇒ x ≤ -
⇒ x ≤ - 2
∵ As the replacement set = {-6, -3, 0, 3, 6, 9}.
Hence, solution set = {-6, -3}.
Solve: 9x - 7 ≤ 28 + 4x; x ∈ W.
Answer
9x - 7 ≤ 28 + 4x
⇒ 9x - 4x ≤ 28 + 7
⇒ 5x ≤ 35
⇒ x ≤
⇒ x ≤ 7
∵ As x is a whole number.
Hence, solution set = {0, 1, 2, 3, 4, 5, 6, 7}.
Solve: -5 (x + 4) > 30; x ∈ Z.
Answer
-5 (x + 4) > 30
⇒ - 5x - 20 > 30
⇒ - 5x > 30 + 20
⇒ - 5x > 50
⇒ x > -
⇒ x > - 10
∵ As x is a integer.
Hence, solution set = {........, - 14, - 13, - 12, - 11}.
Solve : + 15 ≤ 17; x ∈ W.
Answer
+ 15 ≤ 17
Multiply each term with 3 to get:
⇒ + 15 3 ≤ 17 3
⇒ 2x + 1 + 45 ≤ 51
⇒ 2x + 46 ≤ 51
⇒ 2x ≤ 51 - 46
⇒ 2x ≤ 5
⇒ x ≤
⇒ x ≤ 2.5
∵ As x is a whole number.
Hence, solution set = {0, 1, 2}.
Solve: -3 + x < 2, x ∈ N.
Answer
-3 + x < 2
⇒ x < 2 + 3
⇒ x < 5
∵ As x is a natural number.
Hence, solution set = {1, 2, 3, 4}.
Solve and graph the solution set on a number line.
x - 5 < - 2; x ∈ N
Answer
x - 5 < - 2
⇒ x < - 2 + 5
⇒ x < 3
∵ As x is a natural number.
Hence, solution set = {1, 2}.

Solve and graph the solution set on a number line.
3x - 1 > 5; x ∈ W
Answer
3x - 1 > 5
⇒ 3x > 5 + 1
⇒ 3x > 6
⇒ x >
⇒ x > 2
∵ As x is a whole number.
Hence, solution set = {3, 4, 5, 6,.........}.
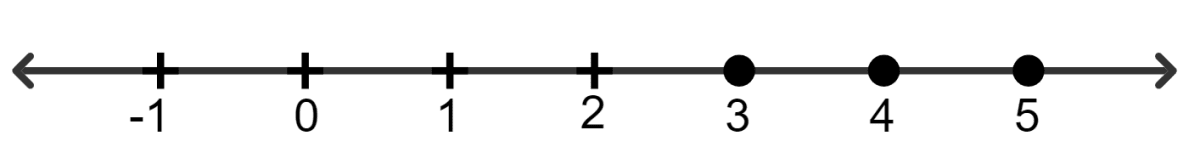
Solve and graph the solution set on a number line.
-3x + 12 < - 15; x ∈ R
Answer
-3x + 12 < - 15
⇒ - 3x < - 15 - 12
⇒ - 3x < - 27
⇒ 3x > 27
⇒ x >
⇒ x > 9
∵ As x is a real number.

Solve and graph the solution set on a number line.
7 ≥ 3x - 8; x ∈ W
Answer
7 ≥ 3x - 8
⇒ 7 + 8 ≥ 3x
⇒ 15 ≥ 3x
⇒ ≥ x
⇒ 5 ≥ x
∵ As x is a whole number.
Hence, solution set = {0, 1, 2, 3, 4, 5}.

Solve and graph the solution set on a number line.
8x - 8 ≤ - 24; x ∈ Z
Answer
8x - 8 ≤ - 24
⇒ 8x ≤ - 24 + 8
⇒ 8x ≤ - 16
⇒ x ≤ -
⇒ x ≤ - 2
∵ As x is a integer.
Hence, solution set = {......., -5, -4, -3, -2}.
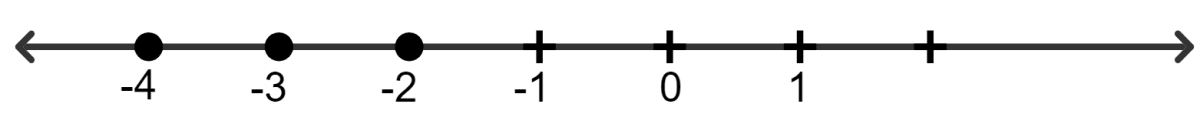
Solve and graph the solution set on a number line.
8x - 9 ≥ 35 - 3x; x ∈ N
Answer
8x - 9 ≥ 35 - 3x
⇒ 8x + 3x ≥ 35 + 9
⇒ 11x ≥ 44
⇒ x ≥
⇒ x ≥ 4
∵ As x is a natural number.
Hence, solution set = {4, 5, 6, 7,..........}.

For each inequation, given below, represent the solution on a number line:
Answer
Multiply each term with 2 to get:
⇒
⇒ 5 - 4x ≥ 1
⇒ - 4x ≥ 1 - 5
⇒ - 4x ≥ - 4
⇒ 4x ≤ 4
⇒ x ≤
⇒ x ≤ 1
∵ As x is a whole number.
Hence, solution set = {0, 1}.

For each inequation, given below, represent the solution on a number line:
3(2x - 1) ≥ 2(2x + 3), x ∈ Z
Answer
3(2x - 1) ≥ 2(2x + 3)
⇒ 6x - 3 ≥ 4x + 6
⇒ 6x - 4x ≥ 3 + 6
⇒ 2x ≥ 9
⇒ x ≥
⇒ x ≥ 4.5
∵ As x is a integer.
Hence, solution set = {5, 6, 7, 8,.......}.

For each inequation, given below, represent the solution on a number line:
2(4 - 3x) ≤ 4(x - 5), x ∈ W
Answer
2(4 - 3x) ≤ 4(x - 5)
⇒ 8 - 6x ≤ 4x - 20
⇒ 8 + 20 ≤ 4x + 6x
⇒ 28 ≤ 10x
⇒ ≤ x
⇒ 2.8 ≤ x
∵ As x is a whole number.
Hence, solution set = {3, 4, 5, 6,.......}.

For each inequation, given below, represent the solution on a number line:
4(3x + 1) > 2(4x - 1), x is a negative integer
Answer
4(3x + 1) > 2(4x - 1)
⇒ 12x + 4 > 8x - 2
⇒ 12x - 8x > - 2 - 4
⇒ 4x > - 6
⇒ x > -
⇒ x > - 1.5
∵ As x is a negative integer.
Hence, solution set = {- 1}.
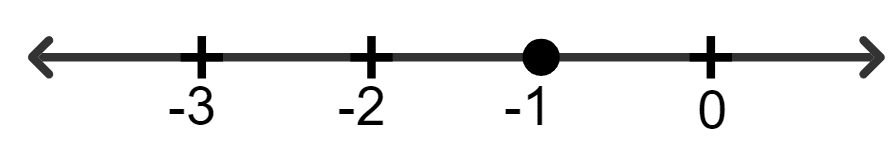
For each inequation, given below, represent the solution on a number line:
< 3, x ∈ R
Answer
On cross multiplying , we get
⇒ 4 - x < 3 2
⇒ 4 - x < 6
⇒ - x < 6 - 4
⇒ - x < 2
⇒ x > - 2
∵ As x is a real number .
Hence, solution set = {x > - 2}.
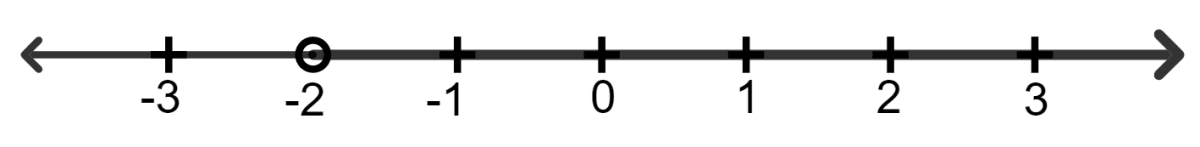
For each inequation, given below, represent the solution on a number line:
-2(x + 8) ≤ 8, x ∈ R
Answer
-2(x + 8) ≤ 8
⇒ -2x - 16 ≤ 8
⇒ -2x ≤ 8 + 16
⇒ -2x ≤ 24
⇒ 2x ≥ - 24
⇒ x ≥ -
⇒ x ≥ - 12
∵ As x is a real number.

If x is a real number and 7(x -2 ) + 2 > 2(5x + 9). Draw the solution set on the number line.
Answer
7(x - 2) + 2 > 2(5x + 9)
⇒ 7x - 14 + 2 > 10x + 18
⇒ 7x - 12 > 10x + 18
⇒ - 18 - 12 > 10x - 7x
⇒ - 30 > 3x
⇒ - > x
⇒ - 10 > x
∵ As x is a real number.
Hence, solution set = {x = ......., - 12, - 11,}.