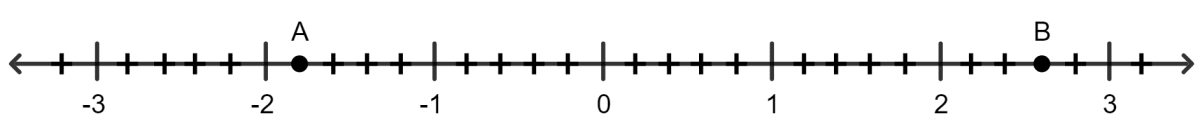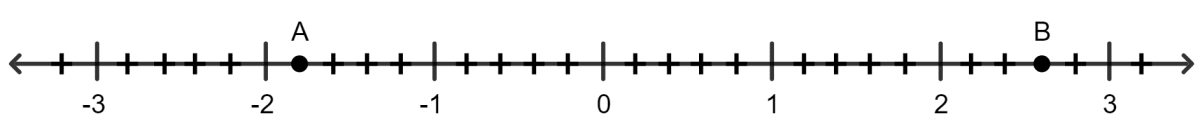A number which is not rational is called
- a natural number
- an integers
- an irrational number
- a whole number
Answer
A number which is not rational is called an irrational number.
Hence, Option 3 is the correct option.
If x ≠ 0 then value of x0 is :
- a rational number
- not a rational number
- not equal to zero
- none of these.
Answer
If x ≠ 0 then value of x0 is a rational number.
Hence, Option 1 is the correct option.
The equation 5x + 7 = 0, gives the value of x which is
- an irrational number
- a whole number
- a rational number
- an integers
Answer
Given,
5x + 7 = 0
⇒ 5x = -7
⇒ x = 5−7
As x is the form of qp where p and q both are integers and q ≠ 0,
∴ x is a rational number.
Hence, Option 3 is the correct option.
Rational number qp is in standard form, if:
- p and q have no common factor and p ≠ 0
- p and q have at least one common factor other than 1 and q ≠ 0
- p and q have no common factor and q ≠ 0
- p is divisible by q completely.
Answer
Rational number qp is in standard form, if p and q have no common factor and q ≠ 0
Hence, Option 3 is the correct option.
The addition of two rational number ba and dc is commutative, if
ba+dc is rational number
b+da+c is a rational number.
ba+dc = dc+ba
ba−dc = dc−ba
Answer
The addition of two rational number ba and dc is commutative, if ba+dc = dc+ba
Hence, Option 3 is the correct option.
−73 + additive inverse of −73 is
1
0
76
−76
Answer
Hence, Option 2 is the correct option.
Add each pair of rational numbers, given below, and show that their addition (sum) is also a rational number:
8−5 and 83
Answer
8−5+83=8−5+3=8−2
As 8−2 is in the form of qp where p and q both are integers and q ≠ 0,
∴ 8−2 is a rational number.
Add each pair of rational numbers, given below, and show that their addition (sum) is also a rational number:
13−8 and 13−4
Answer
13−8+13−4=13−8+(−4)=13−12
As 13−12 is in the form of qp where p and q both are integers and q ≠ 0,
∴ 13−12 is a rational number.
Add each pair of rational numbers, given below, and show that their addition (sum) is also a rational number:
116 and 11−9
Answer
116+11−9=116+(−9)=11−3
As 11−3 is in the form of qp where p and q both are integers and q ≠ 0,
∴ 11−3 is a rational number.
Add each pair of rational numbers, given below, and show that their addition (sum) is also a rational number:
−265 and 398
Answer
−265+39826−5+398
LCM of 26 and 39 is 2 x 3 x 13 = 78
26×3−5×3+39×28×2=78−15+7816=78−15+16=781
As 781 is in the form of qp where p and q both are integers and q ≠ 0,
∴ 781 is a rational number.
Add each pair of rational numbers, given below, and show that their addition (sum) is also a rational number:
−65 and 32
Answer
−65+32=6−5+32
LCM of 6 and 3 is 2 x 3 = 6
6×1−5×1+3×22×2=6−5+64=6−5+4=6−1
As 6−1 is in the form of qp where p and q both are integers and q ≠ 0,
∴ 6−1 is a rational number.
Add each pair of rational numbers, given below, and show that their addition (sum) is also a rational number:
-2 and 52
Answer
−2+52=1−2+52
LCM of 1 and 5 is 5
1×5−2×5+5×12×1=5−10+52=5−10+2=5−8
As 5−8 is in the form of qp where p and q both are integers and q ≠ 0,
∴ 5−8 is a rational number.
Add each pair of rational numbers, given below, and show that their addition (sum) is also a rational number:
−49 and 8−3
Answer
−49+8−34−9+8−3
LCM of 4 and 8 is 2 x 2 x 2 = 8
4×2−9×2+8×1−3×1=8−18+8−3=8−18+(−3)=8−21
As 8−21 is in the form of qp where p and q both are integers and q ≠ 0,
∴ 8−21 is a rational number.
Add each pair of rational numbers, given below, and show that their addition (sum) is also a rational number:
−187 and 278
Answer −187+27818−7+278
LCM of 18 and 27 is 2 x 3 x 3 x 3 = 54
18×3−7×3+27×28×2=54−21+5416=54−21+16=54−5
As 54−5 is in the form of qp where p and q both are integers and q ≠ 0,
∴ 54−5 is a rational number.
Evaluate:
95+6−7
Answer
LCM of 9 and 6 is 2 x 3 x 3 = 18 9×25×2+6×3−7×3=1810+18−21=1810+(−21)=18−11
∴ 95+6−7 = 18−11
Evaluate:
4+−53
Answer
14+5−3
LCM of 1 and 5 is 5
1×54×5+5×1−3×1=520+5−3=520+(−3)=517=352
∴ 4+−53=352
Evaluate:
−151+−125
Answer
15−1+12−5
LCM of 15 and 12 is 2 x 2 x 3 x 5 = 60
15×4−1×4+12×5−5×5=60−4+60−25=60−4+(−25)=60−29
∴ −151+−125=60−29
Evaluate:
95+−43
Answer
95+4−3
LCM of 9 and 4 is 2 x 2 x 3 x 3 = 36
9×45×4+4×9−3×9=3620+36−27=3620+(−27)=36−7
∴ 95+−43 = 36−7
Evaluate:
9−8+12−5
Answer
9−8+12−5
LCM of 9 and 12 is 2 x 2 x 3 x 3 = 36
9×4−8×4+12×3−5×3=36−32+36−15=36−32+(−15)=36−47
∴ 9−8 + 12−5 = 36−47
Evaluate:
0+7−2
Answer
10+7−2
LCM of 1 and 7 is 7
1×70×7+7×1−2×1=70+7−2=70+(−2)=7−2
∴ 0 + 7−2 = 7−2
Evaluate:
−115+0
Answer
11−5+10
LCM of 11 and 1 is 11
11×1−5×1+1×110×11=11−5+110=11−5+0=11−5
∴ −115 + 0 = 11−5
Evaluate:
2+5−3
Answer
12+5−3
LCM of 1 and 5 is 5
1×52×5+5×1−3×1=510+5−3=510+(−3)=57
∴ 2 + 5−3 = 57
Evaluate:
−94+1
Answer
9−4+11
LCM of 9 and 1 is 3 x 3 = 9
9×1−4×1+1×91×9=9−4+99=9−4+9=95
∴ −94 + 1 = 95
Evaluate:
73+9−4+7−11+97
Answer
LCM of 7 and 9 is 3 x 3 x 7 = 63
7×93×9+9×7−4×7+7×9−11×9+9×77×7=6327+63−28+63−99+6349=6327+(−28)+(−99)+49=63−51
∴ 73+9−4+7−11+97=63−51
Evaluate:
32+5−4+31+52
Answer
LCM of 3 and 5 is 3 x 5 = 15
3×52×5+5×3−4×3+3×51×5+5×32×3=1510+15−12+155+156=1510+(−12)+5+6=159
∴ 32+5−4+31+52=159
Evaluate:
74+0+9−8+7−13+917
Answer 74+10+9−8+7−13+917
LCM of 7 ,1 and 9 is 3 x 3 x 7 = 63
7×94×9+1×630×63+9×7−8×7+7×9−13×9+9×717×7=6336+630+63−56+63−117+63119=6336+0+(−56)+(−117)+119=63−18
∴ 74+0+9−8+7−13+917=63−18
Evaluate:
83+12−5+73+123+8−5+7−2
Answer (83+8−5)+(12−5+123)+(73+7−2)=8−2+12−2+71=4−1+6−1+71
LCM of 4 ,6 and 7 is 2 x 2 x 3 x 7 = 84
4×21−1×21+6×14−1×14+7×121×12=84−21+84−14+8412=84(−21)+(−14)+12=84−23
∴ 83+12−5+73+123+8−5+7−2=84−23
For each pair of rational number, verify commutative property of addition of rational numbers.
7−8 and 145
Answer
To prove:
7−8+145=145+7−8
Taking LHS:
7−8+145
LCM of 7 and 14 is 2 x 7 = 14
=7×2−8×2+14×15×1=14−16+145=14−16+5=14−11
Taking RHS:
145+7−8
LCM of 14 and 7 is 2 x 7 = 14
=14×15×1+7×2−8×2=145+14−16=145+(−16)=14−11
∴ LHS = RHS
Hence, 7−8+145=145+7−8
So, the commutative property for the addition of the rational number is verified.
For each pair of rational number, verify commutative property of addition of rational numbers.
95 and −125
Answer
To prove:
95+−125=−125+95
Taking LHS: 95+−125=95+12−5
LCM of 9 and 12 is 2 x 2 x 3 x 3 = 36
=9×45×4+12×3−5×3=3620+36−15=3620+(−15)=365
Taking RHS: −125+95=12−5+95
LCM of 12 and 9 is 2 x 2 x 3 x 3 = 36
=12×3−5×3+9×45×4=36−15+3620=36(−15)+20=365
∴ LHS = RHS
Hence, 95+−125=−125+95
So, the commutative property for the addition of the rational number is verified.
For each pair of rational number, verify commutative property of addition of rational numbers.
5−4 and −15−13
Answer
To prove:
5−4+−15−13=−15−13+5−4
Taking LHS: 5−4+−15−13=5−4+1513
LCM of 5 and 15 is 3 x 5 = 15
=5×3−4×3+15×113×1=15−12+1513=15−12+13=151
Taking RHS: −15−13+5−4=1513+5−4
LCM of 15 and 5 is 3 x 5 = 15
=15×113×1+5×3−4×3=1513+15−12=1513+(−12)=151
∴ LHS = RHS
Hence, 5−4+−15−13=−15−13+5−4
So, the commutative property for the addition of the rational number is verified.
For each pair of rational number, verify commutative property of addition of rational numbers.
−52 and −1511
Answer
To prove:
−52+−1511=−1511+−52
Taking LHS: −52+−1511=5−2+15−11
LCM of 5 and 15 is 3 x 5 = 15
=5×3−2×3+15×1−11×1=15−6+15−11=15−6+(−11)=15−17
Taking RHS: −1511+−52=15−11+5−2
LCM of 15 and 5 is 3 x 5 = 15
=15×1−11×1+5×3−2×3=15−11+15−6=15(−11)+(−6)=15−17
∴ LHS = RHS
Hence, −52+−1511=−1511+−52
So, the commutative property for the addition of the rational number is verified.
For each pair of rational number, verify commutative property of addition of rational numbers.
3 and 7−2
Answer
To prove:
3+7−2=7−2+3
Taking LHS: 3+7−2=13+7−2
LCM of 1 and 7 is 7
=1×73×7+7×1−2×1=721+7−2=721+(−2)=719
Taking RHS: 7−2+3=7−2+13
LCM of 7 and 1 is 7
=7×1−2×1+1×73×7=7−2+721=7(−2)+21=719
∴ LHS = RHS
Hence, 3+7−2=7−2+3
So, the commutative property for the addition of the rational number is verified.
For each pair of rational number, verify commutative property of addition of rational numbers.
-2 and −53
Answer
To prove:
−2+−53=−53+−2
Taking LHS: −2+−53=1−2+5−3
LCM of 1 and 5 is 5
=1×5−2×5+5×1−3×1=5−10+5−3=5−10+(−3)=5−13
Taking RHS: −53+−2=5−3+1−2
LCM of 5 and 1 is 5
=5×1−3×1+1×5−2×5=5−3+5−10=5(−3)+(−10)=5−13
∴ LHS = RHS
Hence, −2+−53=−53+−2
So, the commutative property for the addition of the rational number is verified.
For each set of rational numbers, given below, verify the associative property of addition of rational numbers:
21,32 and 6−1
Answer
To prove:
(21+32)+6−1=21+(32+6−1)
Taking LHS:
(21+32)+6−1 LCM of 2 and 3 is 2 x 3 = 6
=(2×31×3+3×22×2)+6−1=(63+64)+6−1=(63+4)+6−1=67+6−1=67−1=66=1
Taking RHS: 21+(32+6−1)
LCM of 3 and 6 is 2 x 3 = 6 21+(3×22×2+6×1−1×1)=21+(64+6−1)=21+(64+(−1))=21+63
LCM of 2 and 6 is 2 x 3 = 6
=2×31×3+6×13×1=63+63=63+3=66=1
∴ LHS = RHS
(21+32)+6−1=21+(32+6−1)
So, the associative property for the addition of the rational number is verified.
For each set of rational numbers, given below, verify the associative property of addition of rational numbers:
5−2,154 and 10−7
Answer
To prove:
(5−2+154)+10−7=5−2+(154+10−7)
Taking LHS:
(5−2+154)+10−7 LCM of 5 and 15 is 3 x 5 = 15
=(5×3−2×3+15×14×1)+10−7=(15−6+154)+10−7=(15−6+4)+10−7=15−2+10−7 LCM of 15 and 10 is 2 x 3 x 5 = 30
=15×2−2×2+10×3−7×3=30−4+30−21=30−4+(−21)=30−25=6−5
Taking RHS: 5−2+(154+10−7)
LCM of 15 and 10 is 2 x 3 x 5 = 30 5−2+(15×24×2+10×3−7×3)=5−2+(308+30−21)=5−2+(308+(−21))=5−2+30−13
LCM of 5 and 30 is 2 x 3 x 5 = 30
=5×6−2×6+30×1−13×1=30−12+30−13=30−12+(−13)=30−25=6−5
∴ LHS = RHS
(5−2+154)+10−7=5−2+(154+10−7)
So, the associative property for the addition of the rational number is verified.
For each set of rational numbers, given below, verify the associative property of addition of rational numbers:
9−7,−32 and 18−5
Answer
To prove: (9−7+−32)+18−5=9−7+(−32+18−5)
Taking LHS:
(9−7+−32)+18−5=(9−7+3−2)+18−5 LCM of 9 and 3 is 3 x 3 = 9
=(9×1−7×1+3×3−2×3)+18−5=(9−7+9−6)+18−5=(9−7+(−6))+18−5=9−13+18−5
LCM of 9 and 18 is 2 x 9 = 18
=9×2−13×2+18×1−5×1=18−26+18−5=18−26+(−5)=18−31
Taking RHS:
9−7+(−32+18−5)=9−7+(3−2+18−5)
LCM of 3 and 18 is 2 x 3 x 9 = 18
9−7+(3×6−2×6+18×1−5×1)=9−7+(18−12+18−5)=9−7+(18−12+(−5))=9−7+18−17
LCM of 9 and 18 is 2 x 3 x 3 = 18
=9×2−7×2+18×1−17×1=18−14+18−17=18−14+(−17)=18−31
∴ LHS = RHS
(9−7+−32)+18−5=9−7+(−32+18−5)
So, the associative property for the addition of the rational number is verified.
For each set of rational numbers, given below, verify the associative property of addition of rational numbers:
−1,65 and 3−2
Answer
To prove: (−1+65)+3−2=−1+(65+3−2)
Taking LHS:
(−1+65)+3−2=(1−1+65)+3−2 LCM of 1 and 6 is 2 x 3 = 6
=(1×6−1×6+6×15×1)+3−2=(6−6+65)+3−2=(6−6+5)+3−2=6−1+3−2
LCM of 6 and 3 is 2 x 3 = 6
=6×1−1×1+3×2−2×2=6−1+6−4=6−1+(−4)=6−5
Taking RHS: −1+(65+3−2)=1−1+(65+3−2)
LCM of 6 and 3 is 2 x 3 = 6 1−1+(6×15×1+3×2−2×2)=1−1+(65+6−4)=1−1+(65+(−4))=1−1+61
LCM of 1 and 6 is 2 x 3 = 6
=1×6−1×6+6×11×1=6−6+61=6−6+1=6−5
∴ LHS = RHS
(−1+65)+3−2=−1+(65+3−2)
So, the associative property for the addition of the rational number is verified.
Write the additive inverse (negative) of:
8−3
Answer
Additive inverse of 8−3 = −(8−3)
= 83
Write the additive inverse (negative) of:
−94
Answer
−94 =9−4
Additive inverse of 9−4 = −(9−4)
= 94
Write the additive inverse (negative) of:
−13−4
Answer
−13−4 =134
Additive inverse of 134 = −(134)
= −134
Write the additive inverse (negative) of:
0
Answer
0 =10
Additive inverse of 10 = −(10)
= 0
Write the additive inverse (negative) of:
-2
Answer
-2 =1−2
Additive inverse of 1−2 = −(1−2)
= 12=2
Write the additive inverse (negative) of:
1
Answer
1 =11
Additive inverse of 11 = −(11)
= - 11=−1
Fill in the blanks:
(i) Additive inverse of −12−5 = ............... .
(ii) −12−5 + its additive inverse = ............... .
(iii) If ba is the additive inverse of d−c, then d−c is the additive inverse of ............... .
And, so ba+d−c=d−c+ba = ............... .
Answer
(i) Additive inverse of −12−5=−125.
(ii) −12−5 + its additive inverse = 0
(iii) If ba is the additive inverse of d−c, then d−c is the additive inverse of ba.
And, so ba+d−c=d−c+ba=0.
Explanation
(i) −12−5=125
Additive inverse of 125=−125
(ii) 125+(−125)
=125−5=0
(iii) The sum of number and its additive inverse = Additive identity.
State, true or false:
(i) 97=9+57+5
(ii) 97=9−57−5
(iii) 97=9×57×5
(iv) 97=9÷57÷5
(v) −12−5 is a negative rational number.
(vi) 25−13 is smaller than 13−25
Answer
(i) False.
Reason:
9+57+5=1412 ≠ 97
(ii) False
Reason:
9−57−5=42 ≠ 97
(iii) True
Reason:
9×57×5=9×57×5=97
(iv) True
Reason:
9÷57÷5=9×517×51=9×517×51=97
(v) False
Reason:
−12−5=125 is a positive rational number.
(vi) False
Reason:
We need to check if 25−13 is smaller than 13−25
LCM of 25 and 13 is 325
25−13=25×13−13×13=325−169
13−25=13×25−25×25=325−625
And, 325−169 > 325−625
Hence, 25−13 > 13−25
The weight of an empty fruit basket is 231 kg. It contains 565 kg grapes and 883 mangoes. Find the total weight of basket with fruits.
Answer
The weight of an empty fruit basket = 231 kg
The weight of grapes = 565 kg
The weight of mangoes = 883 kg
Total weight of basket with fruits = Weight of empty fruit basket + weight of grapes + weight of mangoes
=231 kg+565 kg+883 kg=37 kg+635 kg+867 kg
LCM of 3, 6 and 8 is 2 x 2 x 2 x 3 = 24
=3×87×8+6×435×4+8×367×3 kg=2456+24140+24201 kg=2456+140+201 kg=24397 kg=162413 kg
Total weight of basket with fruits = 162413
The sum of two rational numbers is 8, if one of them is 243, the other number is
643
641
541
543
Answer
Let x be the other number. 243+x=8⇒411+x=8⇒x=8−411⇒x=18−411
LCM of 1 and 4 is 2 x 2 = 4
⇒x=1×48×4−4×111×1⇒x=432−411⇒x=432−11⇒x=421⇒x=541
The sum of two rational numbers is 8, if one of them is 253, the other number is 541.
Hence, option 3 is correct option.
For three rational numbers ba , dc and fe, we have:
ba−(dc−fe)=ba−dc+fe
ba−(dc−fe)=ba−dc−fe
ba+(dc+fe) ≠ (ba+dc)+fe
ba+(dc+fe)=(ba+dc)+ba+fe
Answer
ba−(dc−fe)=ba−dc+fe
Hence, option 1 is correct option.
The sum of two rational numbers is -6. If one of them is 421, the other number is:
221
121
-121
-1021
Answer
Let x be the other number. 421+x=−6⇒29+x=−6⇒x=−6−29⇒x=1−6−29
LCM of 1 and 2 is 2
⇒x=−1×26×2−2×19×1⇒x=−212−29⇒x=2−12−9⇒x=2−21⇒x=−1021
The sum of two rational numbers is -6, if one of them is 421, the other number is -1021.
Hence, option 4 is correct option.
The number subtracted from 532 to get -132 is :
4
-731
631
731
Answer
Let x be subtracted from 532.
532−x=−132⇒317−x=−35⇒x=317+35⇒x=317+5⇒x=322⇒x=731
The number subtracted from 532 to get -132 is 731.
Hence, option 4 is correct option.
The number added to 532 to get -132 is :
4
-731
631
731
Answer
Let x be added to 532. 532+x=−132⇒317+x=−35⇒x=3−5−317⇒x=3−5−17⇒x=3−22⇒x=−731
The number added to 532 to get -1 32 is -731.
Hence, option 2 is correct option.
Evaluate:
32−54
Answer
32−54
LCM of 3 and 5 is 3 x 5 = 15
3×52×5−5×34×3=1510−1512=1510−12=15−2
Evaluate:
9−4−−32
Answer
9−4−−32=9−4−3−2
LCM of 9 and 3 is 3 x 3 = 9
9×1−4×1−3×3−2×3=9−4−9−6=9−4−(−6)=9−4+6=92
Evaluate:
−1−94
Answer
−1−94=1−1−94
LCM of 1 and 9 is 3 x 3 = 9
1×9−1×9−9×14×1=9−9−94=9−9−4=9−13=−194
Evaluate:
7−2−−143
Answer
7−2−−143=7−2−14−3
LCM of 7 and 14 is 2 x 14 = 14
7×2−2×2−14×1−3×1=14−4−14−3=14−4−(−3)=14−4+3=14−1
Evaluate:
18−5−9−2
Answer
18−5−9−2
LCM of 18 and 9 is 2 x 3 x 3 = 18
18×1−5×1−9×2−2×2=18−5−18−4=18−5−(−4)=18−5+4=18−1
Evaluate:
215−42−13
Answer
215−42−13
LCM of 21 and 42 is 2 x 3 x 7 = 42
21×25×2−42×1−13×1=4210−42−13=4210−(−13)=4210+13=4223
Subtract:
85 from 8−3
Answer
8−3−85=8−3−5=8−8=−1
Subtract:
11−8 from 114
Answer
114−11−8=114−(−8)=114+8=1112=1111
Subtract:
94 from 9−5
Answer
9−5−94=9−5−4=9−9=−1
Subtract:
41 from 8−3
Answer
8−3−41
LCM of 8 and 4 is 2 x 2 x 2 = 8
8×1−3×1−4×21×2=8−3−82=8−3−2=−85
Subtract:
8−5 from 16−13
Answer
16−13−8−5
LCM of 16 and 8 is 2 x 2 x 2 x 2 = 16
16×1−13×1−8×2−5×2=16−13−16−10=16−13−(−10)=16−13+10=16−3
Subtract:
22−9 from 335
Answer
335−22−9
LCM of 33 and 22 is 2 x 3 x 11 = 66
33×25×2−22×3−9×3=6610−66−27=6610−(−27)=6610+27=6637
The sum of two rational numbers is 209. If one of them is 52, find the other.
Answer
Let x be the other number. 52+x=209⇒x=209−52
LCM of 20 and 5 is 2 x 2 x 5 = 20
⇒x=20×19×1−5×42×4⇒x=209−208⇒x=209−8⇒x=201
The sum of two rational numbers is 209, if one of them is 52, the other number is 201
The sum of two rational numbers is 3−2. If one of them is 15−8, find the other.
Answer
Let x be the other number. 15−8+x=3−2⇒x=3−2−15−8
LCM of 3 and 15 is 3 x 5 = 15
⇒x=3×5−2×5−15×1−8×1⇒x=15−10−15−8⇒x=15−10−(−8)⇒x=15−10+8⇒x=15−2
The sum of two rational numbers is 3−2, if one of them is 15−8, the other number is 15−2.
The sum of two rational numbers is -6. If one of them is 5−8, find the other.
Answer
Let x be the other number. 5−8+x=−6⇒x=1−6−5−8
LCM of 1 and 5 is 5
⇒x=1×5−6×5−5×1−8×1⇒x=5−30−5−8⇒x=5−30−(−8)⇒x=5−30+8⇒x=5−22⇒x=−452
The sum of two rational numbers is -6, if one of them is 5−8, the other number is −452.
Which rational number should be added to 8−7 to get 95?
Answer
Let x be added to 8−7.
8−7+x=95⇒x=95−8−7
LCM of 9 and 8 is 2 x 2 x 2 x 3 x 3 = 72
⇒x=9×85×8−8×9−7×9⇒x=7240−72−63⇒x=7240−(−63)⇒x=7240+63⇒x=72103⇒x=17231
The number added to 8−7 to get 95 is 17231.
Which rational number should be added to 9−5 to get 3−2?
Answer
Let x be added to 9−5.
9−5+x=3−2⇒x=3−2−9−5
LCM of 3 and 9 is 3 x 3 = 9
⇒x=3×3−2×3−9×1−5×1⇒x=9−6−9−5⇒x=9−6−(−5)⇒x=9−6+5⇒x=9−1
The number added to 9−5 to get 3−2 is 9−1.
Which rational number should be subtracted from 6−5 to get 94 ?
Answer
Let x be subtracted from 6−5.
6−5−x=94⇒x=6−5−94
LCM of 6 and 9 is 2 x 3 x 3 = 18
⇒x=6×3−5×3−9×24×2⇒x=18−15−188⇒x=18−15−8⇒x=18−23⇒x=−1185
The number subtracted from 6−5 to get 94 is -1185.
What should be subtracted from -2 to get 83 ?
Answer
Let x be subtracted from -2.
−2−x=83⇒1−2−x=83⇒x=1−2−83
LCM of 1 and 8 is 2 x 2 x 2 = 8
⇒x=1×8−2×8−8×13×1⇒x=8−16−83⇒x=8−16−3⇒x=8−19⇒x=−283
The number subtracted from -2 to get 83 is -283.
What should be added to -2 to get 83 ?
Answer
Let x be added to -2.
−2+x=83⇒1−2+x=83⇒x=83−1−2
LCM of 8 and 1 is 2 x 2 x 2 = 8
⇒x=8×13×1−1×8−2×8⇒x=83−8−16⇒x=83−(−16)⇒x=83+16⇒x=819⇒x=283
The number added to -2 to get 83 is 283.
Evaluate:
73+9−4−7−11−97
Answer
(73−7−11)+(9−4−97)=(73−(−11))+(9−4−7)=(714)+(9−11)=(12)+(9−11)
LCM of 1 and 9 is 3 x 3 = 9
=1×92×9+9×1−11×1=918+9−11=918+(−11)=97
Evaluate:
32+5−4−31−52
Answer
(32−31)+(5−4−52)=(32−1)+(5−4−2)=(31)+(5−6)
LCM of 3 and 5 is 3 x 5 = 15
=3×51×5+5×3−6×3=155+15−18=155+(−18)=15−13
Evaluate
74−9−8−7−13+917
Answer
(74−7−13)+(−9−8+917)=(74−(−13))+(98+17)=(74+13)+(925)=(717)+(925)
LCM of 7 and 9 is 3 x 3 x 7 = 63
=7×917×9+9×725×7=63153+63175=63153+175=63328=56313
The number which on multiplying with 532 gives -132 is:
−75
75
−175
517
Answer
Let the number be x. 532×x=−132⇒317×x=−35⇒x=−35÷317⇒x=−35×173⇒x=−3×175×3⇒x=−5115⇒x=−175
Hence, option 3 is the correct option.
If a, b and c are three rational numbers, we have:
- (a x b) x c = (a x c) x (b x c)
- (a + b) x c = (a + c) x (b + c)
- a x (b - c) = a x b - a x c
- a x (b - c) = a x b - c
Answer
We know that, multiplication of rational numbers is distributive over their addition/subtraction.
∴ a x (b - c) = a x b - a x c
Hence, option 3 is the correct option.
The product of a positive rational number and its reciprocal is:
- 0
- -1
- 1
- none
Answer
Let a positive rational number be ba.
ba×ab=b×aa×b=abab=1
Hence, option 3 is the correct option.
The area of a rectangular paper is 731 cm2. If its length 452cm, its breadth is:
153cm
132cm
53cm
6025cm
Answer
Let breadth be b
Length = 452cm = 522cm.
Area = 731 cm2 =322 cm2.
Area of rectangle = length x breadth 322=522×b⇒b=322÷522⇒b=322×225⇒b=3×2222×5⇒b=66110⇒b=35⇒b=132
Hence, option 2 is the correct option.
The product of a rational number 72 and its additive inverse is:
494
7−4
0
1
Answer
Rational number = 72
Additive inverse = −72
72×−72=−7×72×2=−494
Hence, none of the options are correct.
Evaluate:
5−14×7−6
Answer
5−14×7−6=5×7−14×(−6)=3584=512=252
Hence, 5−14×7−6=252
Evaluate:
67×91−18
Answer
67×91−18=6×917×(−18)=546−126=13−3
Hence, 67×91−18=13−3
Evaluate:
72−125×−59
Answer
72−125×−59=72×(−5)−125×9=−360−1125=825=381
Hence, 72−125×−59=381
Evaluate:
9−11×−44−51
Answer
9−11×−44−51=9×−44−11×(−51)=−396561=−1217=−1125
Hence, 9−11×−44−51=−1125
Evaluate:
−516×820
Answer
−516×820=−5×816×20=−40320=−8
Hence, −516×820=−8
Multiply
65 and 98
Answer
65×98=6×95×8=5440=2720
Hence, 65×98=2720
Multiply:
72 and 9−14
Answer
72×9−14=7×92×(−14)=63−28=9−4
Hence, 72×9−14=9−4
Multiply:
8−7 and 4
Answer
8−7×14=8×1−7×4=8−28=2−7=−321
Hence, 8−7×4=−321
Multiply:
−736 and 28−9
Answer
−736×28−9=−7×2836×(−9)=−196−324=4981=14932
Hence, −736×28−9=14932
Multiply:
10−7 and 15−8
Answer
10−7×15−8=10×15−7×(−8)=15056=7528
Hence, 10−7×15−8=7528
Evaluate:
(−32×45)+(95×−103)
Answer
(−3×42×5)+(9×(−10)5×3)=(−1210)+(−9015)=(6−5)+(6−1)=(6−5+(−1))=(6−6)=−1
Hence, (−32×45)+(95×−103)=(6−6)
Evaluate:
(2×41)−(7−18×15−7)
Answer
(1×42×1)−(7×15−18×−7)=(42)−(105126)=(21)−(56) LCM of 2 and 5 is 2 x 5 = 10 =(2×51×5)−(5×26×2)=(105)−(1012)=(105−12)=(10−7)
Hence, (2×41)−(7−18×15−7)=(10−7)
Evaluate:
(−5×152)−(−6×92)
Answer
(1×15−5×2)−(1×9−6×2)=(15−10)−(9−12)=(3−2)−(3−4)=(3−2−(−4))=(3−2+4)=(32)
Hence, (−5×125)−(−6×92)=(32)
Evaluate:
(58×2−3)+(10−3×169)
Answer
(5×28×−3)+(10×16−3×9)=(10−24)+(160−27)=(5−12)+(160−27)
LCM of 5 and 160 is 2 x 2 x 2 x 2 x 2 x 5 = 160
=(5×32−12×32)+(160×1−27×1)=(160−384)+(160−27)=(160−384+(−27))=(160−411)=−216091
Hence, (58×2−3)+(10−3×169)=−216091
Multiply each rational number, given below, by one (1):
−57
Answer
−57×1=−5×17×1=−57
Hence, −57×1=−57
Multiply each rational number, given below, by one (1):
−4−3
Answer
−4−3×1=−4×1−3×1=−4−3=43
Hence, −4−3×1=43
Multiply each rational number, given below, by one (1):
0
Answer
0×1=0
Hence, 0 x 1 = 0
Multiply each rational number, given below, by one (1):
13−8
Answer
13−8×1=13×1−8×1=13−8
Hence, 13−8×1=13−8
Multiply each rational number, given below, by one (1):
−7−6
Answer
−7−6×1=−7×1−6×1=−7−6=76
Hence, −7−6×1=76
For each pair of rational numbers, given below, verify that the multiplication is commutative:
5−1 and 92
Answer
To prove:
5−1×92=92×5−1
Taking LHS:
5−1×92=5×9−1×2=45−2
Taking RHS:
92×5−1=9×52×−1=45−2
∴ LHS = RHS
5−1×92=92×5−1
For each pair of rational numbers, given below, verify that the multiplication is commutative:
−35 and −1113
Answer
To prove:
−35×−1113=−1113×−35
Taking LHS:
−35×−1113=−3×−115×13=3365
Taking RHS:
−1113×−35=−11×−313×5=3365
∴ LHS = RHS
−35×−1113=−1113×−35
For each pair of rational numbers, given below, verify that the multiplication is commutative:
3 and 9−8
Answer
To prove:
3×9−8=9−8×3
Taking LHS:
3×9−8=1×93×−8=9−24=3−8
Taking RHS:
9−8×3=9×1−8×3=9−24=3−8
∴ LHS = RHS
3×9−8=9−8×3
For each pair of rational numbers, given below, verify that the multiplication is commutative:
0 and 17−12
Answer
To prove:
0×17−12=17−12×0
Taking LHS:
0×17−12=1×170×−12=170=0
Taking RHS:
17−12×0=17×1−12×0=170=0
∴ LHS = RHS
0×17−12=17−12×0
Write the reciprocal (multiplicative inverse) of each rational number given below:
5
Answer
The multiplicative inverse of 5 = reciprocal of 5 = 51.
Write the reciprocal (multiplicative inverse) of each rational number given below:
-3
Answer
The multiplicative inverse of -3 = reciprocal of -3 = −31.
Write the reciprocal (multiplicative inverse) of each rational number given below:
115
Answer
The multiplicative inverse of 115 = reciprocal of 115 = 511=251.
Write the reciprocal (multiplicative inverse) of each rational number given below:
−8−7
Answer
The multiplicative inverse of −8−7 = reciprocal of 87 = 78=171.
Write the reciprocal (multiplicative inverse) of each rational number given below:
−7−8
Answer
The multiplicative inverse of −7−8 = reciprocal of 78 = 87.
Find the reciprocal (multiplicative inverse) of:
53×32
Answer
53×32=5×33×2=156=52
The multiplicative inverse of 52 = reciprocal of 52=25=221.
Find the reciprocal (multiplicative inverse) of:
3−8×−713
Answer
3−8×−713=3×−7−8×13=−21−104=21104
The multiplicative inverse of 21104 = reciprocal of 21104 = 10421.
Find the reciprocal (multiplicative inverse) of:
5−3×13−1
Answer
5−3×13−1=5×13−3×(−1)=653
The multiplicative inverse of 653 = reciprocal of 653 = 365=2132.
Verify that (x+y)×z=x×z+y×z, if
x=54,y=3−2 and z=−4
Answer
To prove:
(x+y)×z=x×z+y×z
Taking LHS:
(x+y)×z=(54+3−2)×−4
LCM of 5 and 3 is 3 x 5 = 15
=(5×34×3+3×5−2×5)×−4=(1512+15−10)×−4=(1512+(−10))×−4=(152)×−4=(15×12×−4)=(15−8)
Taking RHS:
x×z+y×z=54×−4+3−2×−4=5×14×−4+3×1−2×−4=5−16+38
LCM of 5 and 3 is 3 x 5 = 15
=5×3−16×3+3×58×5=15−48+1540=15−48+40=15−8
∴ LHS = RHS
(x+y)×z=x×z+y×z
Verify that (x+y)×z=x×z+y×z, if
x=2,y=54 and z=−103
Answer
To prove:
(x+y)×z=x×z+y×z
Taking LHS:
(x+y)×z=(2+54)×−103=(12+54)×−103
LCM of 1 and 5 is 5.
=(1×52×5+5×14×1)×−103=(510+54)×−103=(510+4)×−103=(514)×−103=(5×−1014×3)=(−5042)=(25−21)
Taking RHS:
x×z+y×z=2×−103+54×−103=1×−102×3+5×−104×3=−106+−5012=5−3+25−6
LCM of 5 and 25 is 5 x 5 = 25
=5×5−3×5+25×1−6×1=25−15+25−6=25−15+(−6)=25−21
∴ LHS = RHS
(x+y)×z=x×z+y×z
Verify that x×(y−z)=x×y−x×z, if
x=54,y=4−7 and z=3
Answer
To prove:
x×(y−z)=x×y−x×z
Taking LHS:
x×(y−z)=54×(4−7−3)=54×(4−7−13)
LCM of 4 and 1 is 2 x 2 = 4.
=54×(4×1−7×1−1×43×4)=54×(4−7−412)=54×(4−7−12)=54×(4−19)=(5×44×−19)=(20−76)=(5−19)
Taking RHS:
x×y−x×z=54×4−7−54×3=5×44×−7−5×14×3=20−28−512=5−7−512=5−7−12=5−19
∴ LHS = RHS
x×(y−z)=x×y−x×z
Verify that x×(y−z)=x×y−x×z, if
x=43,y=98 and z=−5
Answer
To prove:
x×(y−z)=x×y−x×z
Taking LHS:
x×(y−z)=43×(98−(−5))=43×(98−1−5)
LCM of 9 and 1 is 3 x 3 = 9.
=43×(9×18×1−1×9−5×9)=43×(98−9−45)=43×(98−(−45))=43×(98+45)=43×(953)=(4×93×53)=(36159)=(1253)
Taking RHS:
x×y−x×z=43×98−43×−5=4×93×8−4×13×−5=3624−4−15=32−4−15
LCM of 3 and 4 is 2 x 2 x 3 = 12
=3×42×4−4×3−15×3=128−12−45=128−(−45)=128+45=1253
∴ LHS = RHS
x×(y−z)=x×y−x×z
Name the multiplication property of rational numbers shown below:
(i) 53×9−8=9−8×53
(ii) 4−3×(75×15−8)=(4−3×75)×15−8
(iii) 54×(−83+7−4)=54×−83+54×7−4
(iv) 5−7×−75=1
(v) −98×1=1×−98=−98
Answer
(i) Commutativity property
Reason
If ba and dc are any two rational numbers, then:
ba×dc=dc×ba
(ii) Associativity property
Reason
If ba,dc and fe are any three rational numbers, then:
ba×(dc×fe)=(ba×dc)×fe
(iii) Distributivity property
Reason
If ba,dc and fe are any three rational numbers, then:
ba×(dc+fe)=(ba×dc)+(ba×fe)
(iv) Existence of inverse
Reason
The multiplicative inverse of ba = reciprocal of ba=ab.
(v) Existence of identity
Reason
For a rational number ba,
1×ba=ba×1=ba.
Fill in the blanks:
(i) The product of two positive rational numbers is always ............... .
(ii) The product of two negative rational numbers is always ............... .
(iii) If two rational numbers have opposite signs then their product is always ............... .
(iv) The reciprocal of a positive rational number is ............... and the reciprocal of a negative rational number is ............... .
(v) Rational number 0 has ............... reciprocal.
(vi) The product of a non-zero rational number and its reciprocal is ............... .
(vii) The numbers ............... and ............... are their own reciprocals.
(viii) If m is reciprocal of n, then the reciprocal of n is ............... .
Answer
(i) The product of two positive rational numbers is always positive.
(ii) The product of two negative rational numbers is always positive.
(iii) If two rational numbers have opposite signs then their product is always negative.
(iv) The reciprocal of a positive rational number is positive and the reciprocal of a negative rational number is negative.
(v) Rational number 0 has no reciprocal.
(vi) The product of a non-zero rational number and its reciprocal is 1.
(vii) The numbers 1 and -1 are their own reciprocal.
(viii) If m is reciprocal of n, then the reciprocal of n is m.
Explanation
(i) Let 2 positive rational numbers be ba and dc.
Hence,
ba×dc=b×da×c=bdac
bdac is also positive rational number.
(ii) Let 2 negative rational numbers be -ba and -dc.
Hence,
−ba×−dc=b×d−a×−c=bdac
bdac is positive rational number.
(iii) Let 2 rational numbers be ba and -dc.
Hence,
ba×−dc=b×da×−c=bd−ac
-bdac is negative rational number.
(iv) Let the positive rational number be ba.
Reciprocal of ba=ab
ab is a positive rational number.
Let the negative rational number be -ba.
Reciprocal of -ba=−ab
-ab is a negative rational number.
(v) Reciprocal of 10=01
01 is not defined.
(vi) Let the positive rational number be ba.
Reciprocal of ba=ab
ba×ab=b×aa×b=abab=1
(vii) Reciprocal of 11=11=1.
Reciprocal of 1−1=−11=−1.
(viii) If reciprocal of 1m=1n
Reciprocal of 1n=1m
The length and breadth of a rectangular piece of paper are 9 cm and 1032 cm respectively. Find:
(i) its area
(ii) its perimeter
Answer
Length = 9 cm
Breadth = 1032 cm
Area = length x breadth
=9×1032=9×332=1×39×32=3288=96 cm2
Area = 96 cm2
Perimeter = 2 x (length + breadth)
=2×(9+1032)=2×(19+332)
LCM of 1 and 3 is 3.
=2×(1×39×3+3×132×1)=2×(327+332)=2×(327+32)=2×(359)=(3×159×2)=(3118)=39(31)
Perimeter = 3931 cm
Hence, area of the rectangular piece of paper is 96 cm2 and its perimeter is 3931 cm.
Find the area and the perimeter of a rectangular piece of land with length 752 m and breadth 461 m.
Answer
Length = 752 m = 537 m
Breadth = 461 = 625m
Area = length x breadth
=537×625=5×637×25=30925=6185=3065 m2
Perimeter = 2 x (length + breadth)
=2×(537+625)
LCM of 5 and 6 is 2 x 3 x 5 = 30.
=2×(5×637×6+6×525×5)=2×(30222+30125)=2×(30222+125)=2×(30347)=(30×1347×2)=(30694)=(15347)=23(152)
Area = 3065 m2 and perimeter = 23152 m
−94 divided by −32 gives:
32
−32
23
−23
Answer
−94÷−32=−94×−23=9×24×3=1812=32
−94 divided by −32 gives 32
Hence, Option 1 is the correct option.
The rational number by which should 21 be divided to get −32 is:
43
−43
34
−34
Answer
Let x be the number.
21÷x=−32⇒21×x1=−32⇒2x1=−32⇒2x=−23⇒x=21×−23⇒x=−2×21×3⇒x=−43
The rational number by which should 21 be divided to get −32 is −43
Hence, Option 2 is the correct option.
For the three rational number a, b and c; which of the following is correct:
- a ÷ b = b ÷ a
- a x (b ÷ c) = (a ÷ b) x (a ÷ c)
- a ÷ (b ÷ c) = (a ÷ b) ÷ (a ÷ c)
- a ÷ (b ÷ c) ≠ a ÷ b ÷ c
Answer
We know that, division of rational numbers is not associative.
∴ a ÷ (b ÷ c) ≠ a ÷ b ÷ c
Hence, Option 4 is the correct option.
The product of two rational numbers is −732. If one of them is 365, the other number is:
- 3
- -3
- 2
- -2
Answer
Let the number be x.
365×x=−732⇒623×x=−323⇒x=−323÷623⇒x=−323×236⇒x=−3×2323×6⇒x=−3×2323×6⇒x=−69138⇒x=−2
Hence, Option 4 is the correct option.
(8 ÷ 3) ÷ (3 ÷ 8) is equal to:
964
649
1
none of the above
Answer
(8÷3)÷(3÷8)=38÷83=38×38=964
Hence, Option 1 is the correct option.
Evaluate:
1 ÷ 31
Answer
1÷31=1×13=1×11×3=13=3
Hence, 1÷31=3
Evaluate:
3÷53
Answer
3÷53=3×35=1×33×5=315=5
Hence, 3÷53=5
Evaluate:
−125÷161
Answer
−125÷161=−125×116=−12×15×16=−1280=−320=−632
Hence, −125÷161=−632
Evaluate:
−1621÷(8−7)
Answer
−1621÷8−7=−1621×−78=16×721×8=112168=23=121
Hence, −1621÷(8−7)=121
Evaluate:
0÷(7−4)
Answer
0÷7−4=0×4−7=1×40×−7=40=0
Hence, 0÷(7−4)=0
Evaluate:
−58÷2524
Answer
−58÷2524=−58×2425=−5×248×25=−120200=−35=−132
Hence, −58÷2524=−132
Evaluate:
−43÷(−9)
Answer
−43÷(−9)=−43×9−1=4×93×1=363=121
Hence, −43÷(−9)=121
Evaluate:
43÷(−125)
Answer
43÷−125=43×−512=−4×53×12=−2036=−59=−154
Hence, 43÷(−125)=−154
Evaluate:
−5÷(−1110)
Answer
−5÷−1110=−5×−1011=1×105×11=1055=211=521
Hence, −5÷(−1110)=521
Evaluate:
11−7÷(44−3)
Answer
11−7÷44−3=−117×−344=11×37×44=33308=328=931
Hence, 11−7÷(44−3)=931
Divide:
3 by 31
Answer
3÷31=3×13=1×13×3=19=9
Hence, 3÷31=9
Divide:
-2 by −21
Answer
−2÷−21=−2×−12=1×12×2=14=4
Hence, −2÷−21=4
Divide:
0 by −97
Answer
0÷−97=0×7−9=1×70×−9=70=0
Hence, 0÷−97=0
Divide:
8−5 by 41
Answer
8−5÷41=8−5×14=8×1−5×4=8−20=2−5=−221
Hence, 8−5÷41=−221
Divide:
−43 by −169
Answer
−43÷−169=−43×−916=4×93×16=3648=34=131
Hence, −43÷−169=131
The product of two rational numbers is -2. If one of them is 74, find the other.
Answer
Let the number be x.
74×x=−2⇒74×x=−12⇒x=−12÷74⇒x=−12×47⇒x=−1×42×7⇒x=−414⇒x=−27⇒x=−321
The other number is −321.
The product of two rational numbers is −94. If one of them is 27−2, find the other.
Answer
Let the number be x.
27−2×x=−94⇒x=−94÷27−2⇒x=−94×2−27⇒x=9×24×27⇒x=18108⇒x=6
The other number is 6.
m and n are two rational numbers such that m×n=−925.
if m=35, find n.
Answer
m×n=−925⇒35×n=−925⇒n=−925÷35⇒n=−925×53⇒n=−9×525×3⇒n=−4575⇒n=−35⇒n=−132
if m=35, then n=−132.
m and n are two rational numbers such that m×n=−925.
if n=−910, find m.
Answer
m×n=−925⇒m×−910=−925⇒m=−925÷−910⇒m=925×109⇒m=9×1025×9⇒m=90225⇒m=25⇒m=221
if n=−910, then n=221.
By what number must −43 be multiplied so that the product is −169?
Answer
Let the number be x
−43×x=−169⇒x=−169÷−43⇒x=169×34⇒x=16×39×4⇒x=4836⇒x=43
−43 must be multiplied by 43 so that the product is −169.
By what number must be −138 multiplied to get 16?
Answer
Let the number be x
−138×x=16⇒x=16÷−138⇒x=−116×813⇒x=−1×816×13⇒x=−8208⇒x=−26
−138 must be multiplied by -26 so that the product is 16
If 321 litres of milk costs ₹49, find the cost of one litre of milk?
Answer
Let the cost of one litre of milk be ₹x.
321×x=49⇒27×x=49⇒x=49÷27⇒x=49×72⇒x=1×749×2⇒x=798⇒x=14
The cost of one litre of milk = ₹14.
Cost of 352 metre of cloth is ₹ 8821. What is the cost of 1 metre of cloth?
Answer
Let the cost of 1 metre of cloth be ₹ x.
352×x=8821⇒517×x=2177⇒x=2177÷517⇒x=2177×175⇒x=2×17177×5⇒x=34885⇒x=26341
Hence, The cost of 1 meter of cloth is ₹ 26341.
Divide the sum of 73 and 14−5 by −21.
Answer
The sum of 73 and 14−5
73+14−5
LCM of 7 and 14 is 2 x 7 = 14
=7×23×2+14×1−5×1=146+14−5=146+(−5)=141
Dividing the sum of 73 and 14−5 by −21
141÷−21=141×−12=−14×11×2=−142=−71
On dividing the sum of 73 and 14−5 by −21 we get −71.
Find (m+n)÷(m−n), if;
m=32 and n=23
Answer
(m+n)÷(m−n)=(32+23)÷(32−23)
LCM of 3 and 2 is 2 x 3 = 6
=(3×22×2+2×33×3)÷(3×22×2−2×33×3)=(64+69)÷(64−69)=(64+9)÷(64−9)=(613)÷(6−5)=613×−56=6×−513×6=−3078=−513
If m = 32 and n = 23 then (m+n)÷(m−n)=−513.
Find (m+n)÷(m−n), if;
m=43 and n=34
Answer
(m+n)÷(m−n)=(43+34)÷(43−34)
LCM of 4 and 3 is 2 x 2 x 3 = 12
=(4×33×3+3×44×4)÷(4×33×3−3×44×4)=(129+1216)÷(129−1216)=(129+16)÷(129−16)=(1225)÷(12−7)=1225×−712=12×−725×12=−84300=−725
If m = 43 and n = 34 then (m+n)÷(m−n)=−725.
Find (m+n)÷(m−n), if;
m=54 and n=−103
Answer
(m+n)÷(m−n)=[54+(−103)]÷[54−(−103)]
LCM of 5 and 10 is 2 x 5 = 10
=[5×24×2+(−10×13×1)]÷[5×24×2−(−10×13×1)]=[108+(−103)]÷[108−(−103)]=[108+(−3)]÷[108−(−3)]=[105]÷[1011]=105×1110=10×115×10=11050=115
If m = 54 and n = -103 then (m+n)÷(m−n)=115.
The product of two rational numbers is -5. If one of these numbers is 15−7, find the other.
Answer
Let the number be x.
15−7×x=−5⇒x=−5÷15−7⇒x=−15×7−15⇒x=1×75×15⇒x=775⇒x=1075
The other number is 1075.
Divide the sum of 85 and 12−11 by the difference of 73 and 145.
Answer
The sum of 85 and 12−11
85+12−11
LCM of 8 and 12 is 2 x 2 x 2 x 3 = 24
=8×35×3+12×2−11×2=2415+24−22=2415+(−22)=24−7
The difference of 73 and 145
73−145
LCM of 7 and 14 is 2 x 7 = 14
=7×23×2−14×15×1=146−145=146−5=141
Dividing the sum of 85 and 12−11 by the difference of 73 and 145,
24−7÷141=24−7×114=−24×17×14=−2498=−1249=−4121
(85+12−11)÷(73−145)=−4121.
The area of a rectangular plate is 575 m2 and its length is 343 m, find its breadth and its perimeter.
Answer
Area of a rectangular plate = 575 m2 = 740 m2
Length of a rectangular plate = 343 m = 415 m
Let the breadth of the rectangular plate be b.
Area = length x breadth
740=415×b⇒b=740÷415⇒b=740×154⇒b=7×1540×4⇒b=105160⇒b=2132⇒b=12111
Perimeter = 2(length + breadth)
=2×(415+2132)
LCM of 4 and 21 is 2 x 2 x 3 x 7 = 84
=2×(4×2115×21+21×432×4)=2×(84315+84128)=2×(84315+128)=2×(84443)=(84443×2)=(84886)=(42443)=104223
Hence, breadth = 12111 and perimeter = 104223
The area of a piece of paper is 7263 cm2 and its breadth is 2139 cm. Find its length and perimeter.
Answer
Area of a rectangular paper = 7263 cm2 = 26185 cm2
Breadth of a rectangular paper = 2139 m = 1335 cm
Let the length of the piece of paper be l.
Area = length x breadth
26185=l×1335⇒l=26185÷1335⇒l=26185×3513⇒l=26×35185×13⇒l=9102405⇒l=1437⇒l=2149
Perimeter = 2(length + breadth)
=2×(1437+1335)
LCM of 14 and 13 is 2 x 7 x 13 = 182
=2×(14×1337×13+13×1435×14)=2×(182481+182490)=2×(182481+490)=2×(182971)=(182971×2)=(1821942)=(91971)=109161
Length = 2149 and perimeter = 109161
In the following number line, points A and B represent:
−251 and 253
251 and 253
−154 and 253
−51 and 52
Answer
In this number line, there are 5 small lines between every 2 consecutive integers, which means moving one step left from 0 gives −51.
Point A is 4 step left from -1. So, A = −154
Point B is 3 step right from 2. So, B = 253
Hence, Option 3 is the correct option.
Using the number line, given below; the length of line segment AB is:
513 = 253
−513 = −253
452
1514
Answer
As we know, A = −154 and B = 253.
Length = 59+513 =59+13=522=452
Hence, Option 3 is the correct option.
The rational number between ba and dc is:
21(ba−dc)
(b−da−c)
(b+da+c)
(b+ca+d)
Answer
For any two rational numbers ba and dc, (b+da+c) is also a rational number with its value lying between ba and dc.
Hence, Option 3 is the correct option.
The rational number between 31 and 21 is:
73 and 83
52 and 0
61 and 32
32 and 23
Answer
As we know that, for any two rational numbers ba and dc, (b+da+c) is also a rational number with its value lying between ba and dc.
The rational number between 31 and 21 is (3+21+1)
= (52)
The rational number between 31 and 52 is (3+51+2)
= (83)
The rational number between 21 and 52 is (2+51+2)
= (73)
73 and 83 are two rational number between 31 and 21
Hence, option 1 is the correct option.
The rational numbers −47 and 43 are represented by:
B and E respectively
C and D respectively
C and E respectively
B and F respectively
Answer
In this number line, there are 4 small lines between every 2 consecutive integers, which means moving one step towards left from 0 gives −41.
Point C is 3 step left from -1. So, C = −143=−47
Point E is 3 step right from 0. So, E = 43
∴ −47 and 43 are represented by C and E, respectively.
Hence, option 3 is the correct option.
Draw a number line and mark
43,47,4−3 and 4−7 on it.
Answer
Draw a number line as shown below:
In this number line
OA = AB = ...............= OA' = A'B' = 1 unit
Since the denominator of each given rational number is 4, divide each OA, AB, BC, OA', A'B',etc into four equal parts.
To represent 41, move one step towards the right side of 0 to reach P as shown.
As, OA = 1 unit, therefore OP = 41 unit.
Hence, to represent 43, move 3 steps towards the right side of 0 to reach point Q. So, Q represent 43.
In the same way to represent 4−3, move 3 steps towards the left side of 0 to reach point R. So, R represent 4−3.
So, S represent 47 and T represent 4−7.
On a number line mark the points
32,3−8,37,3−2 and -2.
Answer
Draw a number line as shown below:
In this number line
OA = AB = ...............= OA' = A'B' = 1 unit
Since the denominator of each given rational number is 3, divide each OA, AB, BC, OA', A'B', etc into three equal parts.
To represent 31, move one step towards the right side of 0 to reach P as shown.
As, OA = 1 unit, therefore OP = 31 unit.
Hence, to represent 32, move 2 steps towards the right side of 0 to reach point Q. So, Q represents 32.
In the same way to represent 3−2, move 2 steps towards the left side of 0 to reach point R. So, R represents 3−2.
Similarly, S represents 3−8, T represents 37 and B' represents -2.
Insert one rational number between
53 and 85
Answer
As we know that, for any two rational numbers ba and dc, (b+da+c) is also a rational number with its value lying between ba and dc.
The rational number between 53 and 85 is (5+83+5)
= (138)
Hence, one rational number between 53 and 85 is 138.
Insert one rational number between
21 and 2
Answer
As we know that, for any two rational numbers ba and dc, (b+da+c) is also a rational number with its value lying between ba and dc.
The rational number between 21 and 12 is (2+11+2)
= (33)
=1
Hence, one rational number between 21 and 2 is 1.
Insert two rational numbers between:
75 and 83
Answer
As we know that, for any two rational numbers ba and dc, (b+da+c) is also a rational number with its value lying between ba and dc.
Given numbers = 75 and 83
=75,7+85+3,83=75,158,83=75,7+155+8,158,83=75,2213,158,83
Hence, required rational numbers between 75 and 83 are : 2213 and 158
Insert three rational numbers between:
118 and 94
Answer
As we know that, for any two rational numbers ba and dc, (b+da+c) is also a rational number with its value lying between ba and dc.
Given numbers = 118 and 94
=118,11+98+4,94=118,2012,94=118,53,94=118,11+58+3,53,94=118,1611,53,94=118,1611,53,5+93+4,94=118,1611,53,147,94=118,1611,53,21,94
Hence, required rational numbers between 118 and 94 are : 1611,53 and 21
Insert five rational numbers between 53 and 32
Answer
LCM of 5 and 3 is 3 x 5 = 15
Make denominator of each given rational number equal to 15 (the LCM).
53=5×33×3=159
and
32=3×52×5=1510
Since five rational numbers are required between 53 and 32; multiply the numerator and the denominator of each rational number by 5 + 1 = 6.
∴159=15×69×6=9054
and
1510=15×610×6=9060
⇒ Required rational numbers between 53 and 32 are : 9054,9055,9056,9057,9058,9059,9060
= 53,1811,4528,3019,4529,9059,32
Hence, 1811,4528,3019,4529 and 9059 lie between 53 and 32.
Insert six rational numbers between 65 and 98.
Answer
LCM of 6 and 9 is 2 x 3 x 3 = 18
Make denominator of each given rational number equal to 18 (the LCM).
65=6×35×3=1815
and
98=9×28×2=1816
Since six rational numbers are required between 65 and 98; multiply the numerator and the denominator of each rational number by 6 + 1 = 7.
1815=18×715×7=126105
and
1816=18×716×7=126112
Required rational numbers between 65 and 98 are : 126105,126106,126107,126108,126109,126110,126111,126112
= 65,6353,126107,76,126109,6355,4237,98
Hence, 65,6353,126107,76,126109 and 4237 lie between 65 and 98.
Insert seven rational numbers between 2 and 3.
Answer
2 = 12
3 = 13
Since seven rational numbers are required between 12 and 13; multiply the numerator and the denominator of each rational number by 7 + 1 = 8.
12=1×82×8=816
and
13=1×83×8=824
Required rational numbers between 12 and 13 are : 816,817,818,819,820,821,822,823,824
= 12,817,49,819,25,821,411,823,13
= 2,281,241,283,221,285,243,287,3
Hence, 281,241,283,221,285,243 and 287 lie between 2 and 3.
50 is a rational number, 80 is a rational number, then 50÷80 is:
an irrational number
a rational number
0
undefined
Answer
50÷80=50×08=5×00×8=00 00 is undefined.
Hence, option 4 is the correct option.
a and b are two rational numbers such that a + b = 0; then :
a = b
a and b are numerically equal
a and b are numerically equal but opposite in sign
none of the above
Answer
a + b = 0
a = 0 - b
a = -b
a and b are numerically equal but opposite in sign.
Hence, option 3 is the correct option
The product of rational number 83 and its additive inverse is :
1
0
649
−649
Answer
Additive inverse of 83 = −83
83×−83=−8×83×3=−649
Hence, option 4 is the correct option.
The sum of rational number 32 and its reciprocal is:
1
261
0
65
Answer
Reciprocal of 32 = 23
We need to find the sum of 32 and 23
32+23
LCM of 3 and 2 is 2 x 3 = 6
3×22×2+2×33×3=64+69=64+9=613=261
Hence, option 2 is the correct option.
The product of two rational numbers is -1, if one of them is 52, then the other is :
−52
25
−25
none of these
Answer
Let the number be x.
52×x=−1⇒52×x=−11⇒x=−11÷52⇒x=−11×25⇒x=−1×21×5⇒x=−25
Hence, option 3 is the correct option.
Statement 1: For a rational number 97,97−0=97 and 0−97=−97. Hence, Subtraction has only right identity.
Statement 2: Subtraction has no identity.
Which of the following options is correct?
Both the statement are true.
Both the statement are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Answer
For a rational number 97,97−0=97 and 0−97=−97
We know that,
For any number a,
a - 0 = a and 0 - a ≠ 0
Thus, subtraction only has right identity.
So, statement 1 is true.
Subtraction has 0 as right identity element.
So, statement 2 is false.
Hence, option 3 is the correct option.
Assertion (A) : Additive inverse of 52 is −25.
Reason (R) : For every non-zero rational number 'a', '-a' such that a + (-a) = 0.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
The additive inverse of a number a is a number -a such that :
⇒ a + (-a) = 0.
So, reason (R) is true.
According to Assertion: Additive inverse of 52 is −25.
⇒52+(−25)⇒52−25⇒104−1025⇒104−25⇒10−21=0
So, assertion (A) is false.
Hence, option 4 is the correct option.
Assertion (A) : Multiplicative inverse of −57 is −75.
Reason (R) : For every non-zero rational number 'a', there is a rational number a1 such that a×a1=1.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
We know that,
The multiplicative inverse of any number a is it's reciprocal i.e. a1.
So, reason (R) is true.
The reciprocal of −57=−571=−75.
So, assertion (A) is true.
∴ Both A and R are true and R is correct reason for A.
Hence, option 1 is the correct option.
Assertion (A) : 21+2=25, which is a rational number.
Reason (R) : If qp and sr are any two rational numbers then qp+sr=sr+qp.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
According to Assertion:
⇒21+2⇒21+24⇒21+4⇒25
A number is rational if it can be written in the form qp, where p and q are integers.
Since, 25 is in the form of qp as well as 5 and 2 are integers.
So, assertion (A) is true.
According to commutative property of addition: When two numbers are added together, then a change in their positions does not change the result.
When qp and sr are any two rational numbers then qp+sr=sr+qp, as addition of rational numbers is a commutative property.
So, reason (R) is true but it does not explain assertion.
Hence, option 2 is the correct option.
Assertion (A) : 0 and 1211 are two rational numbers and 1211=0 then 0 ÷ 1211=0, a rational number.
Reason (R) : If a rational number is divided by some non - zero rational number, the result is always a rational number.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
When 0 is divided by any non-zero number, the result is 0.
⇒ 0 ÷ 1211=0
Since, 0 = 10 is in the form of qp.
So, assertion (A) is true.
The division of a rational number ba by another non-zero rational number dc is:
⇒ba÷dc⇒ba×cd⇒bcad
Since, bcad is in the form of qp.
So, reason is true. But it does not explains about assertion.
Hence, option 2 is the correct option.
Write the rational number that does not have a reciprocal.
Answer
The rational number is 10
The reciprocal of 10=01 (not defined).
Hence, 0 is the rational number that does not have a reciprocal.
Write the rational numbers that are equal to their reciprocal.
Answer
Reciprocal of 11=11=1.
Reciprocal of 1−1=−11=−1.
The numbers 1 and -1 are their own reciprocal.
Write the reciprocal of −178+17−8.
Answer
−178+17−8=17−8+(−8)=17−16
The reciprocal of 17−16=−1617.
Write five rational numbers between −23 and 35
Answer
LCM of 2 and 3 is 2 x 3 = 6
Make denominator of each given rational number equal to 6 (the LCM).
−23=−2×33×3=−69
and
35=3×25×2=610
The rational number between −69 and 610 are −68,−67,−66,−65,−64,−63,−62,−61,60,61,62,63,64,65,66,67,68,69
From these rational numbers we can take any five rational number.
Hence, required rational numbers between −23 and 35 are :
−68,−66,−64,−62,62
= −34,−11,−32,−31,31
Hence, −131,−1,−32,−31 and 31 lies between −23 and 35.
Write five rational number greater than -4.
Answer
There are infinite many rational number between -4 and ∞.
Hence, -3, -2, -1, 1, 2 are five rational number greater than -4.
What should be added to −221 to get −331?
Answer
Let x be added to −221.
−221+x=−331⇒−25+x=−310⇒x=−310−2−5
LCM of 3 and 2 is 2 x 3 = 6
⇒x=3×2−10×2−2×3−5×3⇒x=6−20−6−15⇒x=6−20−(−15)⇒x=6−20+15⇒x=6−5
The number added to −221 to get −331 is 6−5.
Which should be subtracted from 221 to get −331 ?
Answer
Let x be subtracted from 221.
221−x=−331⇒25−x=−310⇒x=25−3−10
LCM of 2 and 3 is 2 x 3 = 6
⇒x=2×35×3−3×2−10×2⇒x=615−6−20⇒x=615−(−20)⇒x=615+20⇒x=635⇒x=565
The number subtracted from 221 to get −331 is 565.
If m=−97 and n=65, verify that:
m - n ≠ n - m
Answer
To prove:
m - n ≠ n - m
LHS:
m−n−97−65
LCM of 9 and 6 is 2 x 3 x 3 = 18
−9×27×2−6×35×3=−1814−1815=18−14−15=18−29=−11811
RHS:
n−m65−(−97)=65+97
LCM of 6 and 9 is 2 x 3 x 3 = 18
=6×35×3+9×27×2=1815+1814=1815+14=1829=11811
Hence, LHS ≠ RHS
m - n ≠ n - m
If m=−97 and n=65, verify that:
-(m + n) = (-m) + (-n)
Answer
To prove:
-(m + n) = (-m) + (-n)
LHS:
−(m+n)−(−97+65)
LCM of 9 and 6 is 2 x 3 x 3 = 18
=−(−9×27×2+6×35×3)=−(−1814+1815)=−(18−14+15)=−(181)
RHS:
(−m)+(−n)=−(−97)+(−65)=(97)+(−65)
LCM of 9 and 6 is 2 x 3 x 3 = 18
=(9×27×2)+(−6×35×3)=(1814)+(−1815)=(1814+(−15))=(18−1)
Hence, LHS = RHS
∴−(m+n)=(−m)+(−n)
Represent rational numbers −37 and 47 on the same number line.
Answer
The rational numbers are −37 and 47.
LCM of 3 and 4 is 2 x 2 x 3 = 12
Hence, the rational number will be-
−3×47×4,4×37×3=−1228,1221=−2124,1129
Draw a number line as shown below:
In this number line OA = AB = ........... = OA' = A'B' = 1 unit
Since, the denominator of each given rational numbers is 12, divide each of OA, AB,...,OA', A'B', etc. into twelve equal parts.
To represent 121, moves one step towards the right side of O to reach point P as shown.
Hence, OA = 1 unit , therefore OP = 121 unit and so P represents 121.
In the same way, to represent −2124 , move 4 steps toward the left side of B' to reach point Q. Clearly, Q represents −37.
Similarly, to represent 1129 , move 9 steps toward the right side of A to reach point R. Clearly, R represents 47.
Add: −65 and 83
Answer
LCM of 6 and 8 is 2 x 2 x 2 x 3 = 24
−6×45×4+8×33×3=−2420+249=24−20+9=24−11
∴ −65+83=−2411
Subtract: 83 from −65
Answer
LCM of 8 and 6 is 2 x 2 x 2 x 3 = 24
−6×45×4−8×33×3=−2420−249=24−20−9=24−29=−1245
∴ −65−83=−1245
Multiply: −65 and 83
Answer
−65×83=6×8−5×3=48−15=−165
−65×83=−165
Divide: 83 by −65
Answer
83÷−65=83×−56=8×53×(−6)=40−18=−209
83÷−65=−209
By what number should 1712 be multiplied to get −74?
Answer
Let the number be x
1712×x=−74⇒x=−74÷1712⇒x=−74×1217⇒x=−7×124×17⇒x=−8468⇒x=−2117
−2117 must be multiplied by 1712 so that the product is −74.
By what number should 1712 be divided to get −74?
Answer
Let the number be x
1712÷x=−74⇒1712×x1=−74⇒x=1712×−47⇒x=−17×412×7⇒x=−6884⇒x=−1721⇒x=−1174
−1174 must be divided by 1712 so that the product is −74.