Two sides of a triangle are 12 cm and 15 cm. If the height of the triangle corresponding to 12 cm side is 10 cm, then the height of the triangle corresponding to 15 cm side is:
4 cm
12 cm
8 cm
16 cm
Answer
Given:
Sides of the triangle = 12 cm, 15 cm
Height of the triangle = 10 cm
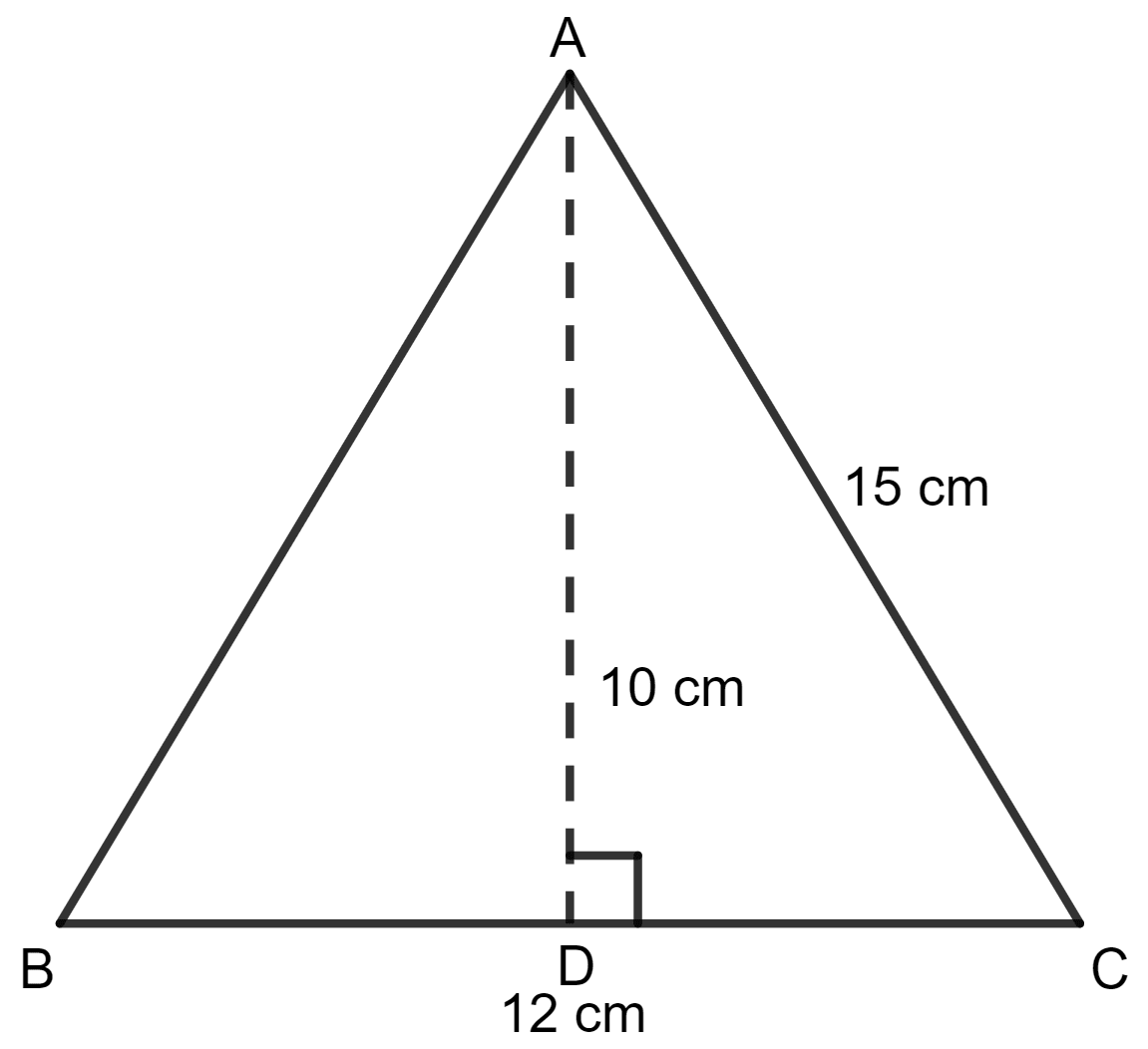
As we know, the area of the triangle = x side x height
= x 12 x 10 cm2
= x 120 cm2
= 60 cm2
When, side of the triangle = 15 cm
Let the height of the triangle = h cm
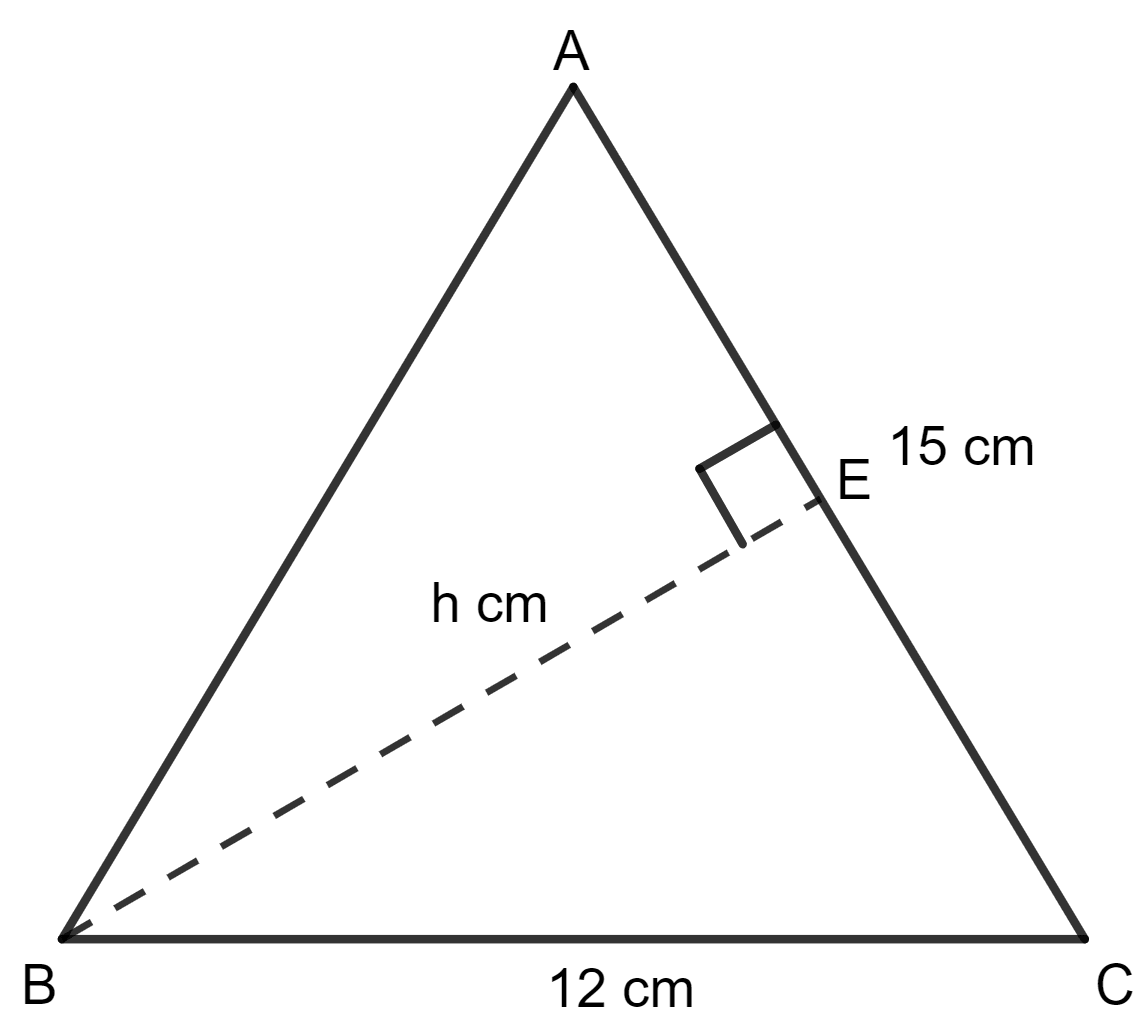
As we know, the area of the triangle = x side x height
= x 15 x h 2
[∵ Both areas remain same since they represent the area of the same triangle.]
⇒ x 15 x h = 60
⇒ 15 x h = 2 x 60
⇒ 15 x h = 120
⇒ h =
⇒ h = 8 cm
Hence, the height of the triangle corresponding to 15 cm side is 8 cm.
Hence, option 3 is the correct option.
The base of a right-angled triangle is 8 cm and its hypotenuse is 10 cm. The area of the triangle is:
80 cm2
40 cm2
48 cm2
24 cm2
Answer
Given:
Base of the triangle = 8 cm
Hypotenuse of the triangle = 10 cm
Let h be the height of the triangle.
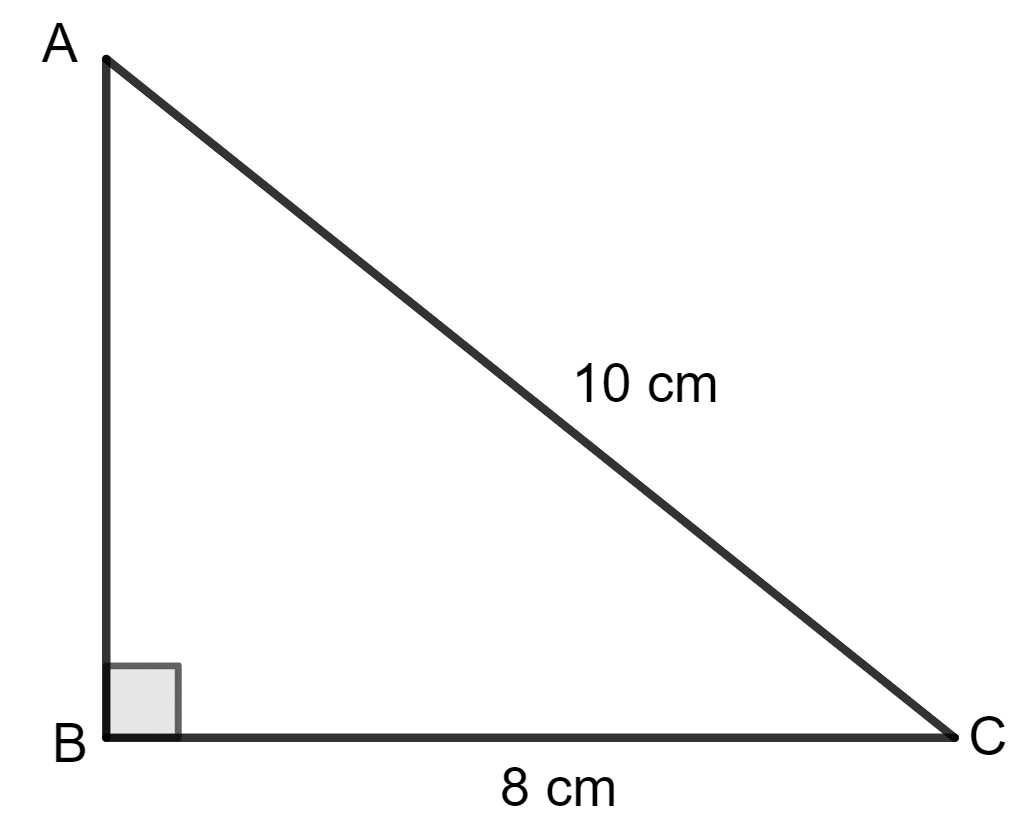
In a right-angled triangle, using the Pythagorean theorem,
Base2 + Height2 = Hypotenuse2
⇒ (8)2 + h2 = (10)2
⇒ 64 + h2 = 100
⇒ h2 = 100 - 64
⇒ h2 = 36
⇒ h =
⇒ h = 6 cm
As we know, the area of the triangle = x side x height
= x 8 x 6 cm2
= x 48 cm2
= 24 cm2
Hence, option 4 is the correct option.
The area of a triangle with sides 4 cm, 3 cm and 5 cm is:
12 cm2
15 cm2
10 cm2
6 cm2
Answer
Let a = 4 cm, b = 3 cm and c = 5 cm.
∵ Area of triangle =
= cm2
= cm2
= cm2
= 6 cm2
Hence, option 4 is the correct option.
The altitude of an isosceles triangle is 4 cm and its base is 2 cm more than its height. The area of the triangle is :
24 cm2
12 cm2
16 cm2
8 cm2
Answer
Given:
Altitude of the triangle = 4 cm
Base of the triangle = 2 cm more than its height
= 2 + 4 cm
= 6 cm
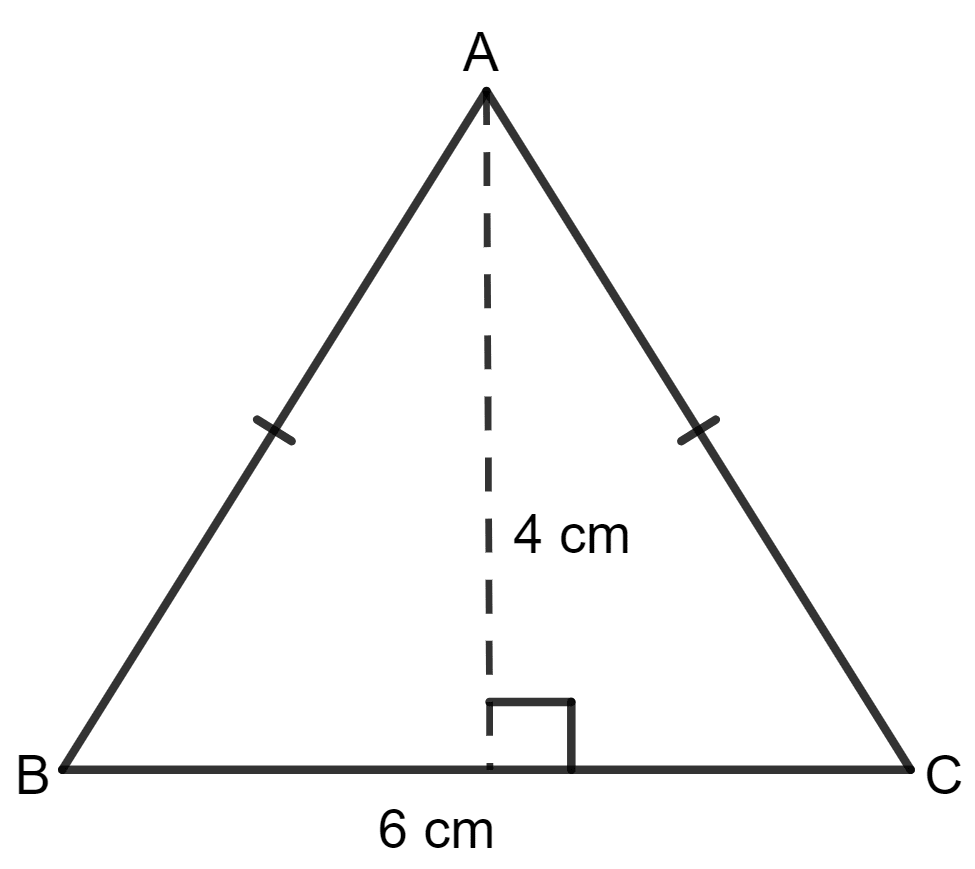
∵ As we know, the area of the triangle = x side x height
= x 6 x 4 cm2
= x 24 cm2
= 12 cm2
Hence, option 2 is the correct option.
Area of an equilateral triangle with each side 6 cm is:
cm
cm
cm
cm
Answer
Given:
Side of the equilateral triangle = 6 cm
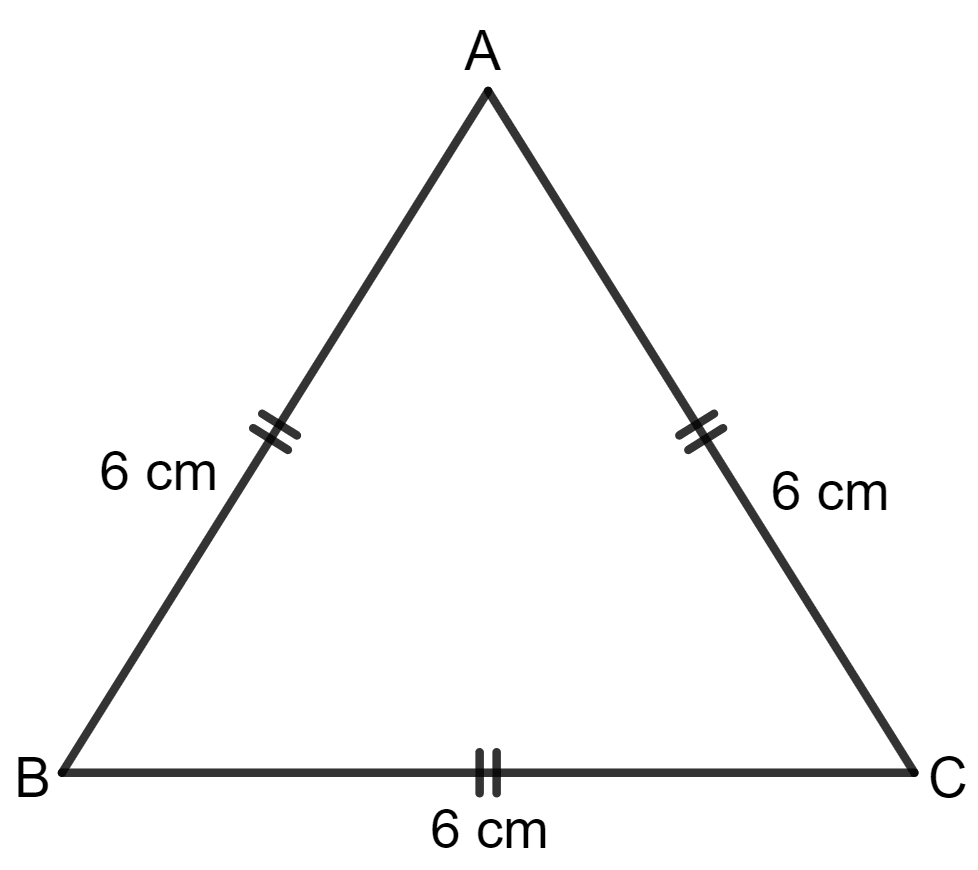
∵ As we know, the area of the equilateral triangle =
= cm2
= cm2
= cm2
Hence, option 2 is the correct option.
Find the area of a triangle whose sides are:
10 cm, 24 cm and 26 cm
Answer
Let a = 10 cm, b = 24 cm and c = 26 cm.
∵ Area of triangle =
= cm2
= cm2
= cm2
= 120 cm2
Hence, area of triangle = 120 cm2.
Two sides of a triangle are 6 cm and 8 cm. If the height of the triangle corresponding to 6 cm side is 4 cm; find :
(i) area of the triangle
(ii) height of the triangle corresponding to 8 cm side.
Answer
(i) Given:
Side of the triangle = 6 cm
Height of the triangle = 4 cm
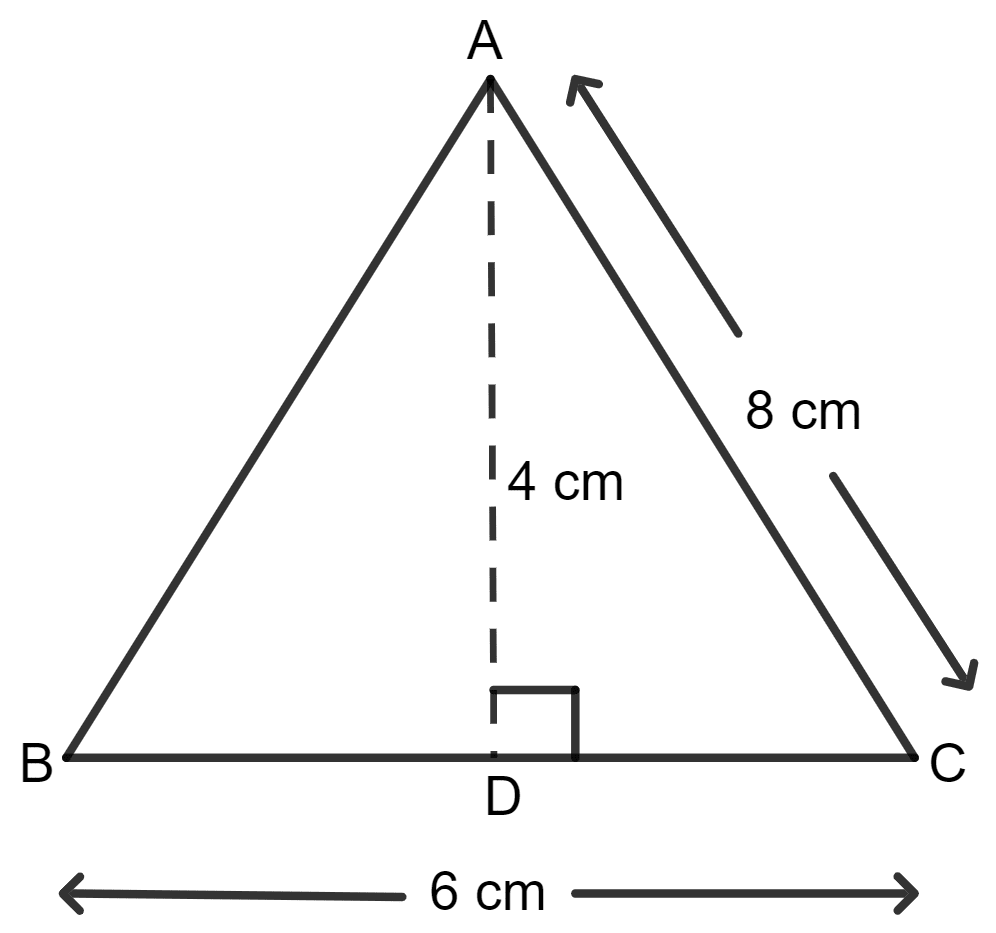
As we know, the area of the triangle = x side x height
= x 6 x 4 cm2
= x 24 cm2
= 12 cm2
Hence, area of triangle = 12 cm2.
(ii) When, the side of the triangle = 8 cm
Let the height of the triangle be h cm
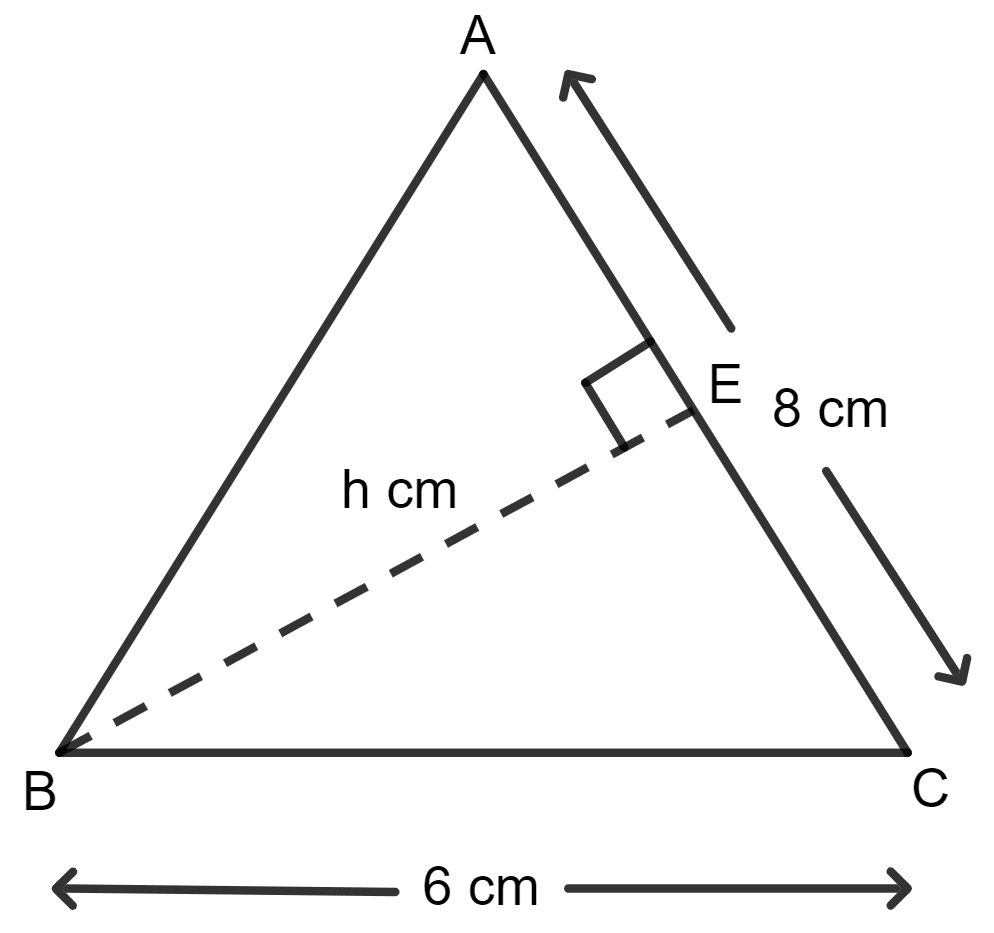
As we know area of triangle = x side x height
= x 8 x h 2
[∵ Both areas remain same since they represent the area of the same triangle.]
⇒ x 8 x h = 12
⇒ 4 x h = 12
⇒ h =
⇒ h = 3 cm
Hence, height of the triangle corresponding to 8 cm side is 3 cm.
The sides of a triangle are 16 cm, 12 cm and 20 cm. Find:
(i) area of the triangle
(ii) height of the triangle corresponding to the largest side
(iii) height of the triangle corresponding to the smallest side.
Answer
(i) Let a = 16 cm, b = 12 cm and c = 20 cm.
∵ Area of triangle =
= cm2
= cm2
= cm2
= 96 cm2
Hence, area of triangle = 96 cm2.
(ii) When, the largest side of the triangle = 20 cm
Let the height of the triangle = h cm
As we know, the area of the triangle = x side x height
= x 20 x h
[∵ Both areas remain same since they represent the area of the same triangle.]
⇒ x 20 x h = 96
⇒ 10 x h = 96
⇒ h =
⇒ h = 9.6
Hence, height of the triangle corresponding to 20 cm side is 9.6 cm.
(iii) When, the smallest side of the triangle = 12 cm
Let the height of the triangle = h cm
As we know, the area of the triangle = x side x height
= x 12 x h
[∵ Both areas remain same since they represent the area of the same triangle.]
⇒ x 12 x h = 96
⇒ 6 x h = 96
⇒ h =
⇒ h = 16 cm
Hence, height of the triangle corresponding to 12 cm side is 16 cm.
The base and the height of a triangle are in the ratio 4 : 5. If the area of the triangle is 40 m2, find its base and height.
Answer
Given:
The base and the height of a triangle are in the ratio 4 : 5.
The area of the triangle = 40 m2
Let the base of the triangle be 4x m.
And, the height of the triangle be 5x m.
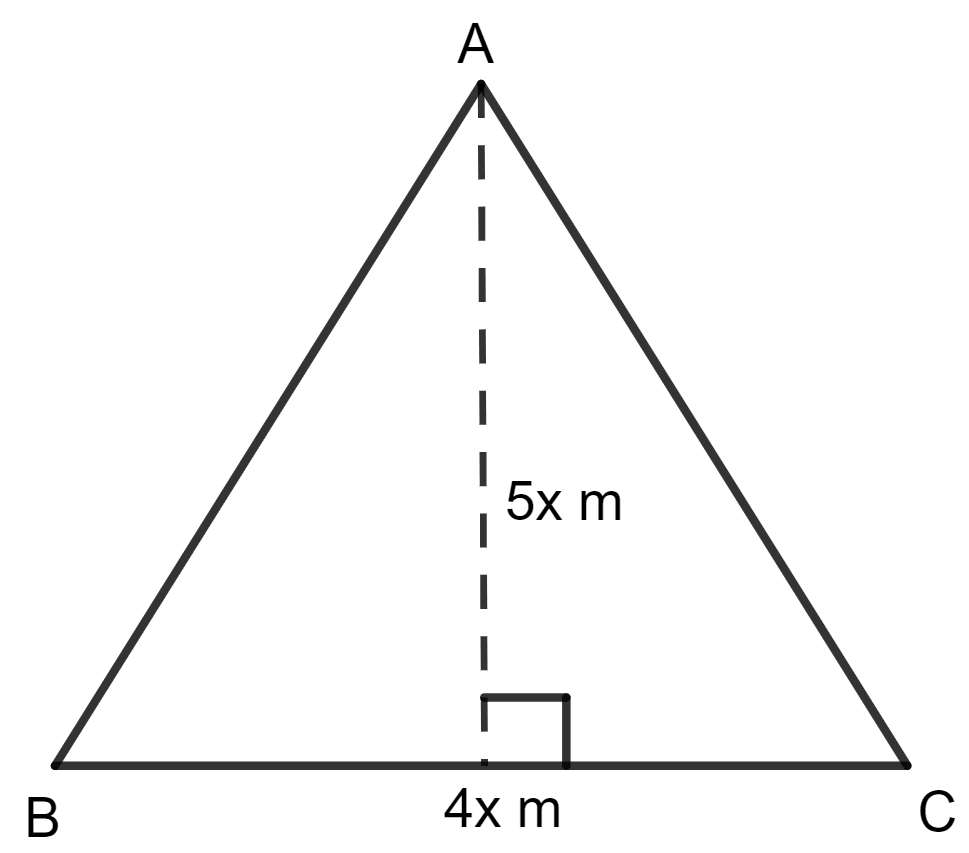
As we know, the area of a triangle = side height
⇒ 4x 5x = 40 m2
⇒ 20x2 = 40 m2
⇒ 10x2 = 40 m2
⇒ x2 = m2
⇒ x2 = 4 m2
⇒ x = m
⇒ x = 2 m
So, base of the triangle = 4x
= 4 x 2 m
= 8 m
And, height of the triangle = 5x
= 5 x 2 m
= 10 m
Hence, base and height of the triangle are 8 m and 10 m, respectively.
The base and the height of a triangle are in the ratio 5 : 3. If the area of the triangle is 67.5 m2; find its base and height.
Answer
Given:
The base and the height of a triangle are in the ratio 5 : 3.
The area of the triangle = 67.5 m2
Let the base of the triangle = 5x m
And, the height of the triangle = 3x m
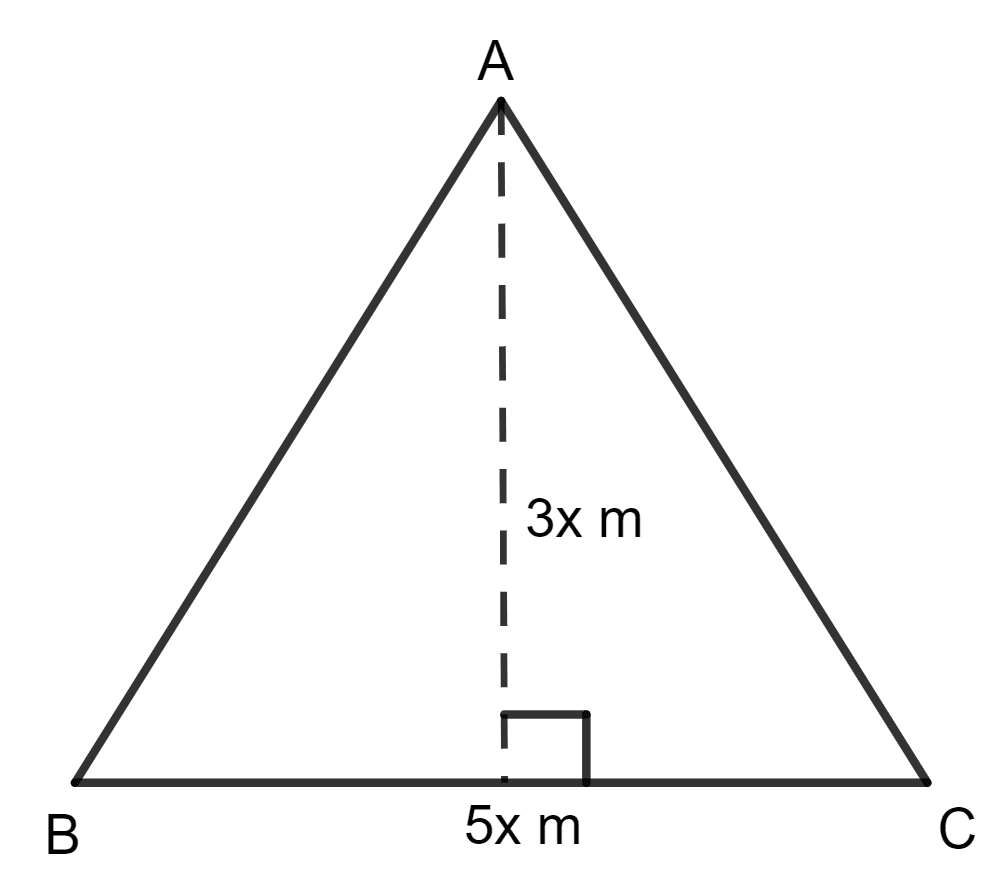
As we know, the area of the triangle = x side x height
⇒ x 5x x 3x = 67.5 m2
⇒ x 15x2 = 67.5 m2
⇒ 15x2 = 2 67.5 m2
⇒ 15x2 = 135 m2
⇒ x2 = m2
⇒ x2 = 9 m2
⇒ x = m
⇒ x = 3 m
So, base of the triangle = 5x
= 5 x 3 m
= 15 m
And, height of the triangle = 3x
= 3 x 3 m
= 9 m
Hence, base and height of the triangle are 15 m and 9 m, respectively.
The area of an equilateral triangle is ; find its perimeter.
Answer
Let the side of the equilateral triangle be a.
It is given that the area of an equilateral triangle is .
∵ As we know, the area of the equilateral triangle =
⇒
⇒
⇒
⇒
⇒
⇒
⇒ a = 24 cm
Now, perimeter of equilateral triangle = 3 x side
= 3 x 24 cm
= 72 cm
Hence, the perimeter of the triangle is 72 cm.
The area of an equilateral triangle is numerically equal to its perimeter. Find its perimeter correct to 2 decimal places.
Answer
Let the side of the equilateral triangle be a.
∵ As we know, the area of the equilateral triangle =
And, perimeter of equilateral triangle = 3 x side
It is given that the area of an equilateral triangle is numerically equal to its perimeter.
⇒
⇒
⇒
⇒
⇒
⇒
⇒
⇒
As we know perimeter of equilateral triangle = 3 x side
= 3 x unit
= 12 unit
= 12 x 1.74 unit
= 20.78 unit
Hence, the perimeter of the triangle is 20.78 unit.
A field is in the shape of a quadrilateral ABCD in which side AB = 18 m, side AD = 24 m, side BC = 40 m, DC = 50 m and angle A = 90°. Find the area of the field.
Answer
Join BD and the field is divided into two triangular fields.
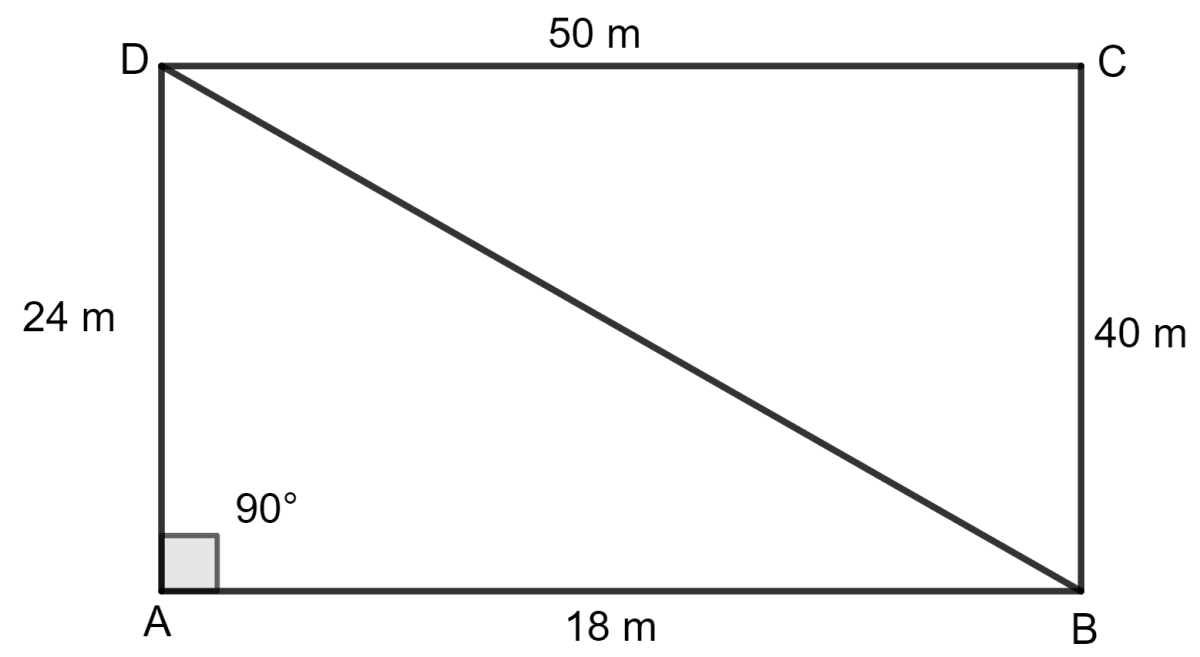
Triangle ABD is a right angled triangle.
AB = 18 m
AD = 24 m
Let BD be h m.
By using the Pythagorean theorem,
Base2 + Height2 = Hypotenuse2
⇒ (18)2 + (24)2 = h2
⇒ 324 + 576 = h2
⇒ h2 = 900
⇒ h =
⇒ h = 30 m
For the right-angled triangle ABD,
As we know, the area of a triangle = x base x height
= x 18 x 24 m2
= x 432 m2
= 216 m2
For triangle BCD,
Let a = 40 m, b = 50 m and c = 30 m.
∵ Area of triangle =
= m2
= m2
= m2
= 600 m2
Area of rectangular field = Area of triangle ABD + Area of triangle BCD
= 216 + 600 m2
= 816 m2
Hence, the area of the field is 816 m2.
The lengths of the sides of a triangle are in the ratio 4 : 5 : 3 and its perimeter is 96 cm. Find its area.
Answer
Given:
Perimeter of the triangle = 96 cm
The lengths of the sides of a triangle are in the ratio 4 : 5 : 3.
Let the length of the sides of the triangle be 4a, 5a and 3a.
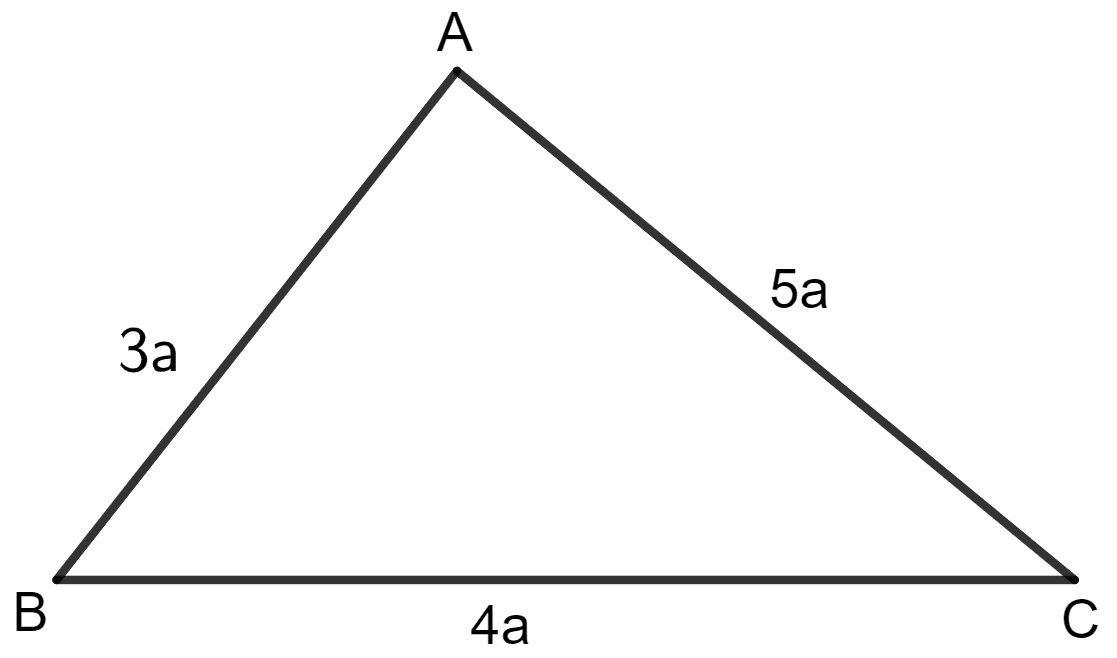
∵ Perimeter of triangle = sum of sides of the triangle.
⇒ 4a + 5a + 3a = 96 cm
⇒ 12a = 96 cm
⇒ a = cm
⇒ a = 8 cm
So, the lengths of the sides are 4a, 5a and 3a.
= 4 x 8, 5 x 8 and 3 x 8
= 32, 40 and 24
Let a = 32 m, b = 40 m and c = 24 m.
∵ Area of triangle =
= cm2
= cm2
= cm2
= 384 cm2
Hence, the area of the triangle is 384 cm2.
One of the equal sides of an isosceles triangle is 13 cm and its perimeter is 50 cm. Find the area of the triangle.
Answer
Given:
One of the equal sides of an isosceles triangle = 13 cm
Perimeter of the triangle = 50 cm
Let a be the length of the third side of the triangle.
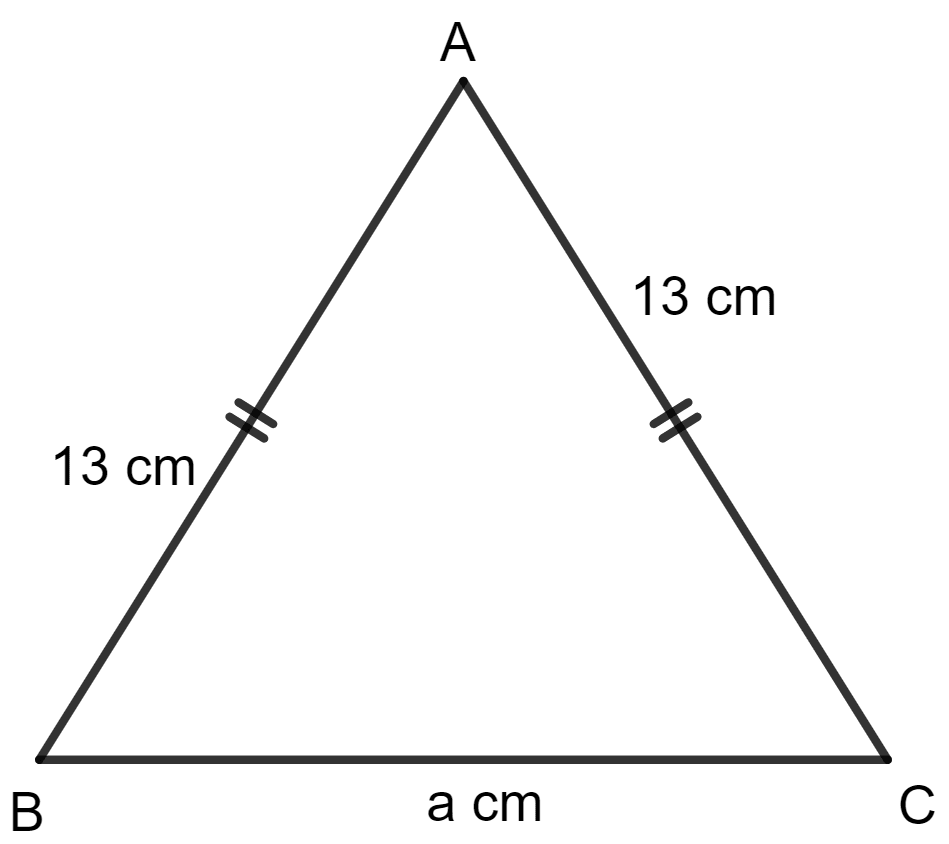
∵ Perimeter of triangle = sum of sides
⇒ 13 + 13 + a = 50 cm
⇒ 26 + a = 50 cm
⇒ a = 50 - 26 cm
⇒ a = 24 cm
Let a = 13 m, b = 13 m and c = 24 m.
∵ Area of triangle =
= cm2
= cm2
= cm2
= 60 cm2
Hence, the area of the triangle is 60 cm2.
The altitude and the base of a triangular field are in the ratio 6 : 5. If its cost is ₹ 49,57,200 at the rate of ₹ 36,720 per hectare and 1 hectare = 10,000 sq.m, find (in metre) the dimensions of the field.
Answer
Given:
Ratio of altitude and base of the field = 6 : 5
Total cost = ₹ 49,57,200
Rate = ₹ 36,720 per hectare
As we know that area of the triangular field x rate = total cost
⇒ Area of the triangular field x = ₹ 49,57,200
⇒ Area of the triangular field = ₹
⇒ Area of the triangular field = ₹
⇒ Area of the triangular field = 13,50,000 m2
Let the altitude be 6a and the base be 5a.
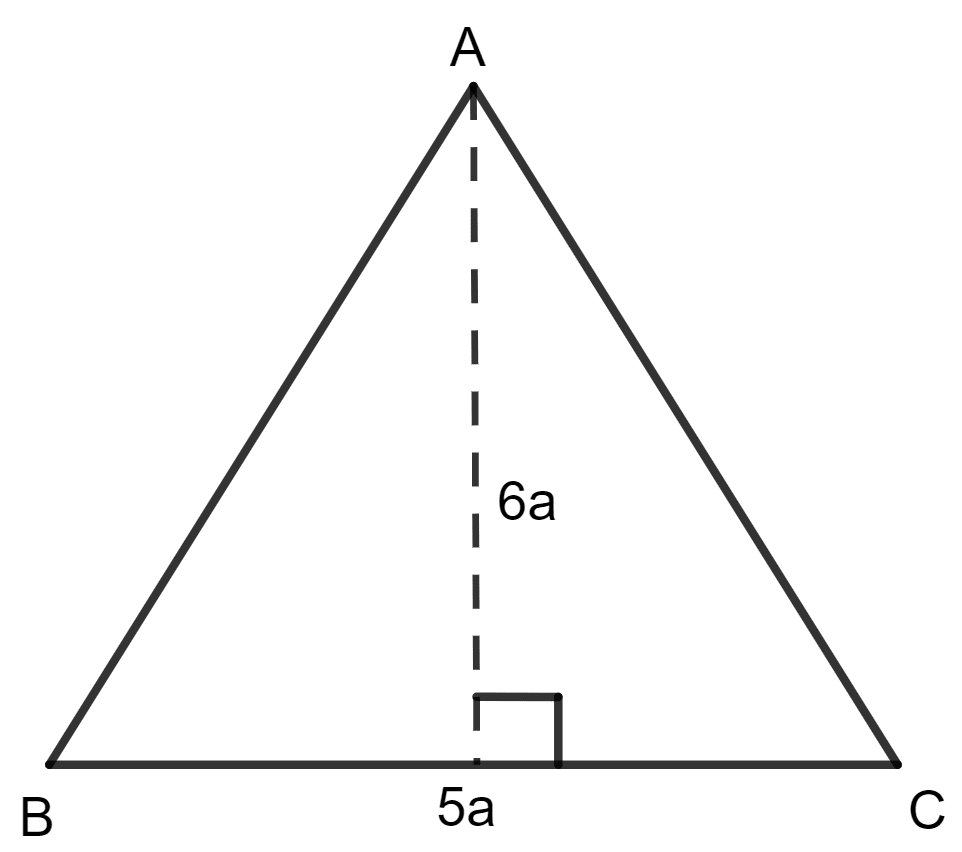
As we know, the area of a triangle = x base x height
⇒ 13,50,000 = x 6a x 5a
⇒ 13,50,000 = x 30a2
⇒ 13,50,000 = 15a2
⇒ a2 =
⇒ a2 = 90000
⇒ a =
⇒ a = 300
So, the altitude = 6a
= 6 x 300
= 1800 m
And, the base = 5a
= 5 x 300
= 1500 m
Hence, the dimensions of the field are 1800 m and 1500 m.
Find the area of the right-angled triangle with hypotenuse 40 cm and one of the other two sides 24 cm.
Answer
Given:
Base of the triangle = 24 cm
Hypotenuse of the triangle = 40 cm
Let h be the height of the triangle.
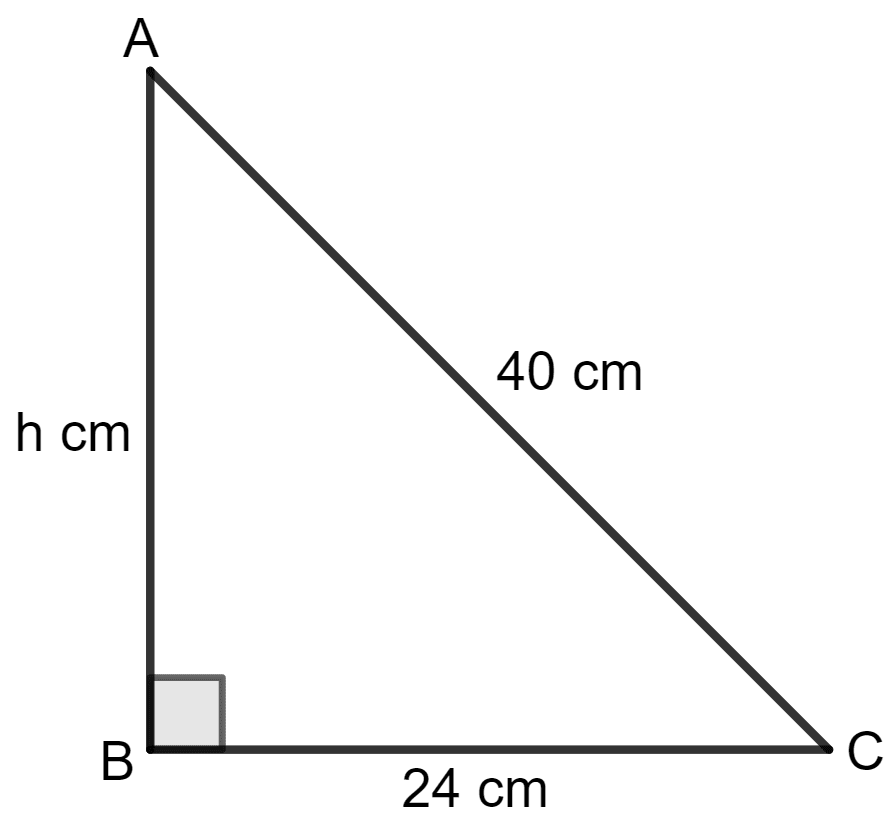
In a right-angled triangle, using the Pythagorean theorem,
Base2 + Height2 = Hypotenuse2
⇒ (24)2 + h2 = (40)2
⇒ 576 + h2 = 1600
⇒ h2 = 1600 - 576
⇒ h2 = 1024
⇒ h =
⇒ h = 32 cm
As we know, the area of a triangle = x side x height
= x 24 x 32 cm2
= x 768 cm2
= 384 cm2
Hence, the area of the triangle is 384 cm2.
Use the information given in the given figure to find:
(i) the length of AC.
(ii) the area of △ ABC.
(iii) the length of BD, correct to one decimal place.
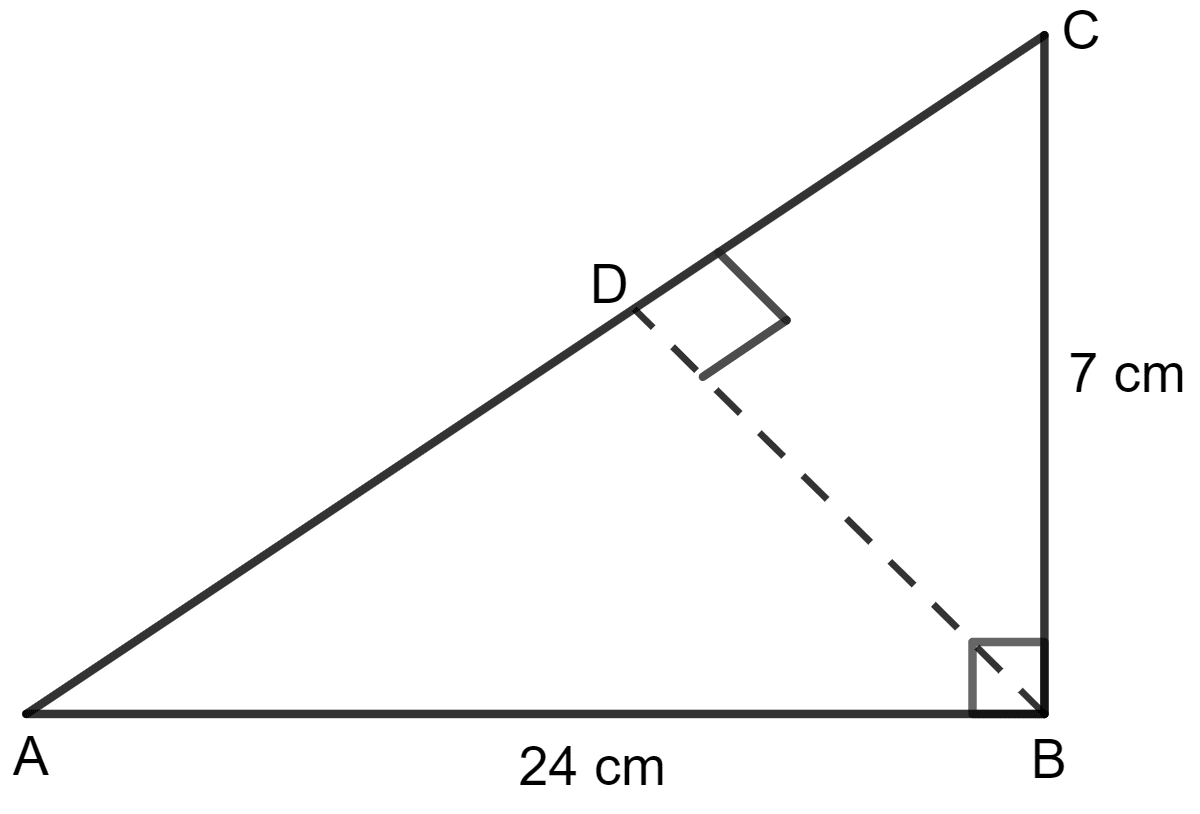
Answer
(i) Given:
In triangle ABC,
Base of the triangle = 24 cm
Height of the triangle = 7 cm
Let h be the hypotenuse of the triangle.
In a right-angled triangle, using the Pythagorean theorem,
Base2 + Height2 = Hypotenuse2
⇒ (24)2 + (7)2 = h2
⇒ 576 + 49 = h2
⇒ h2 = 625
⇒ h =
⇒ h = 25 cm
Hence, the length of AC = 25 cm.
(ii) As we know, the area of a triangle = x side x height
= x 24 x 7 cm2
= x 168 cm2
= 84 cm2
Hence, the area of the triangle = 84 cm2.
(iii) The base of the triangle = 25 cm
Let the height of the triangle be h.
As we know, the area of a triangle = x side x height
[∵ Both areas remain same since they represent the area of the same triangle.]
⇒ x 25 x h = 84
⇒ 25 x h = 2 x 84
⇒ 25 x h = 168
⇒ h =
⇒ h = 6.7 cm
Hence, the length of BD = 6.7 cm.
The length and the breadth of a rectangle are in the ratio 9 : 5. If its area is 180 m2; the length (longest side) of the rectangle is :
36 m
20 m
10 m
18 m
Answer
Given:
The length and the breadth of a rectangle are in the ratio 9 : 5.
The area of the rectangle is 180 m2.
Let the length of the rectangle be 9a and the breadth of the rectangle be 5a.
As we know, the area of the rectangle = length x breadth
⇒ 180 m2 = 9a x 5a
⇒ 180 m2 = 45a2
⇒ a2 = m2
⇒ a2 = 4 m2
⇒ a = m
⇒ a = 2 m
So, the length of the rectangle is 9a.
= 9 x 2 m
= 18 m
Hence, option 4 is the correct option.
The adjacent sides of a rectangle are 16 m and 9 m. The length of the square whose area is equal to the area of the rectangle is :
16 m
18 m
12 m
72 m
Answer
Given:
The adjacent sides of the rectangle are 16 m and 9 m.
As we know, the area of the rectangle = length x breadth
= 16 x 9 m2
= 144 m2
SInce the area of the rectangle is equal to the area of the square,
And, the area of the square = side2
⇒ side2 = 144 m2
⇒ side = m
⇒ side = 12 m
Hence, option 3 is the correct option.
The area of a square, with perimeter 16 cm is :
16 cm2
8 cm2
12 cm2
128 cm2
Answer
Given:
The perimeter of the square is 16 cm.
As we know, the perimeter of a square = 4 x side.
⇒ 4 x side = 16 cm
⇒ side = cm
⇒ side = 4 cm
And, the area of the square = side2
= (4)2 cm2
= 16 cm2
Hence, option 1 is the correct option.
The perimeter of square with area 169 m2 is :
52 m
26 m
39 m
19.5 m2
Answer
Given:
The area of the square is 169 m2.
Let the side of the square be x m.
As we know, the area of a square = side2
⇒ x2 = 169 m2
⇒ x = m
⇒ x = 13 m
And, the perimeter of the square = 4 x side
= 4 x 13 m
= 52 m
Hence, option 1 is the correct option.
The area of square with diagonal 10 cm is:
100 cm2
50 cm2
25 cm2
75 cm2
Answer
Given:
The diagonal of the square is 10 cm.
Let each side of the square be a cm.
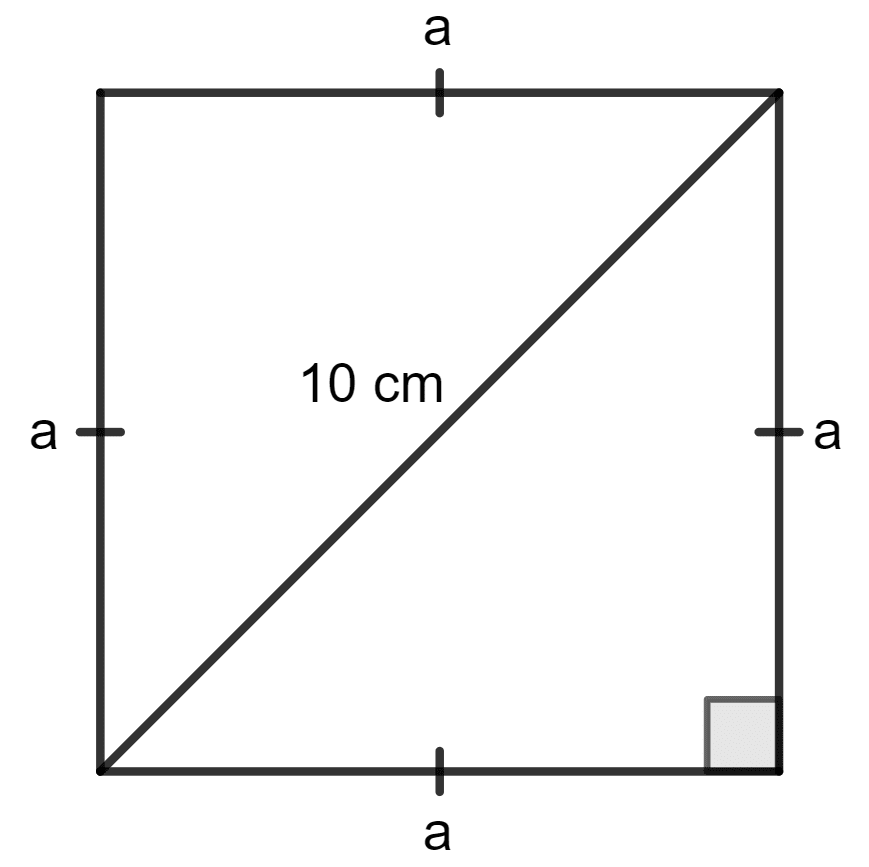
Then, by using the Pythagoras theorem,
⇒ Diagonal2 = Side2 + Side2
⇒ (10)2 = a2 + a2
⇒ 100 = 2a2
⇒ a2 =
⇒ a2 = 50
⇒ a =
⇒ a = 5
As we know, the area of a square = side2
= (5 ) 2 cm2
= 25 x 2 cm2
= 50 cm2
Hence, option 2 is the correct option.
Find the length and perimeter of a rectangle, whose area = 120 cm2 and breadth = 8 cm.
Answer
Given:
The breadth of the rectangle is 8 cm.
The area of the rectangle is 120 cm2.
Let the length of the rectangle be l.
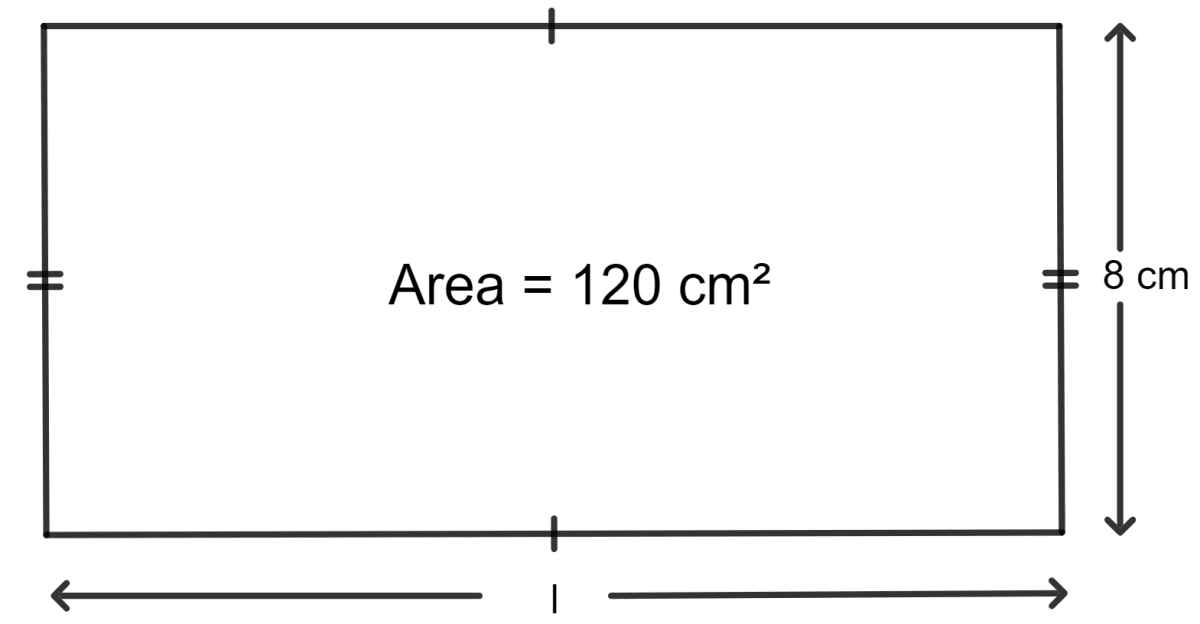
As we know, the area of the rectangle = length x breadth
⇒ l x 8 = 120
⇒ l =
⇒ l = 15 cm
The perimeter of the rectangle = 2(length + breadth)
= 2 (15 + 8)
= 2 x 23
= 46 cm
Hence, the length of the rectangle is 15 cm, and the perimeter is 46cm.
The perimeter of a rectangle is 46 m and its length is 15 m. Find its :
(i) breadth
(ii) area
(iii) diagonal
Answer
(i) Given:
The perimeter of the rectangle is 46 m.
The length of the rectangle is 15 m.
Let the breadth of the rectangle be b m.
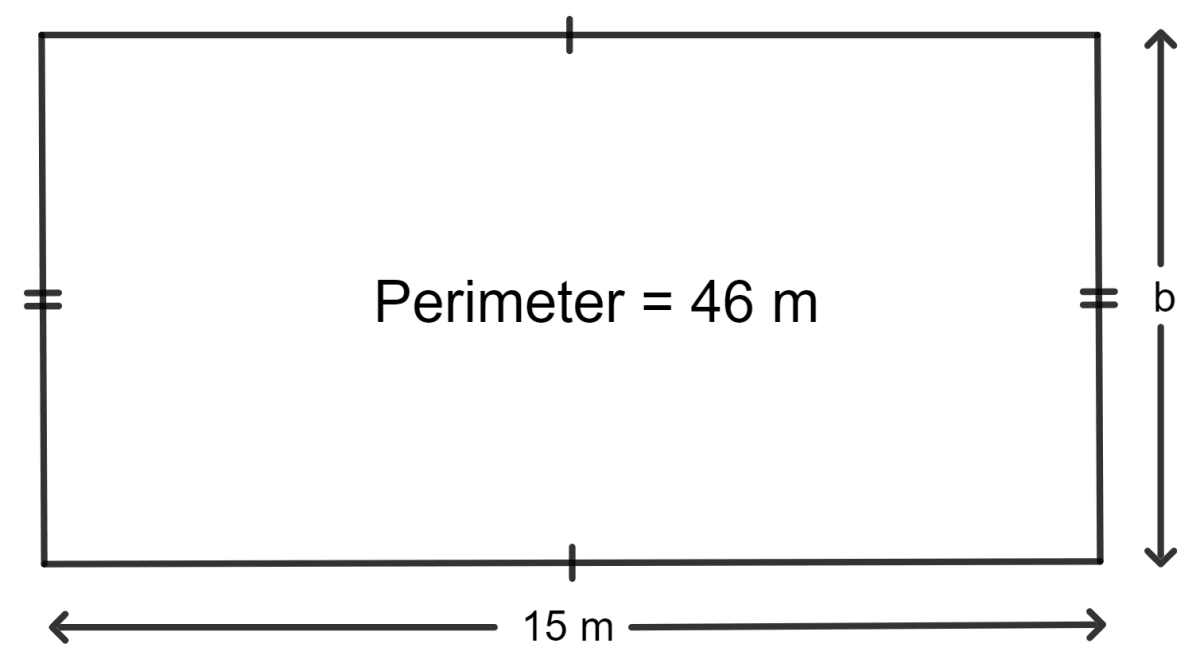
As we know, the perimeter of the rectangle = 2(length + breadth)
⇒ 2(15 + b) = 46
⇒ 15 + b =
⇒ 15 + b = 23
⇒ b = 23 - 15
⇒ b = 8 m
Hence, the breadth of the rectangle is 8 m.
(ii) The area of the rectangle = length x breadth
= 15 x 8 m2
= 120 m2
Hence, the area of the rectangle is 120 m2.
(iii) By using Pythagoras theorem,
⇒ Diagonal2 = Length2 + Breadth2
⇒ Diagonal2 = 152 + 82
⇒ Diagonal2 = 225 + 64
⇒ Diagonal2 = 289
⇒ Diagonal =
⇒ Diagonal = 17 m
Hence, the diagonal of the rectangle is 17 m.
The diagonal of a rectangle is 34 cm. If its breadth is 16 cm, find its :
(i) length
(ii) area
Answer
Given:
The diagonal of the rectangle is 34 cm.
The breadth of the rectangle is 16 cm.
Let the length of the rectangle be l cm.
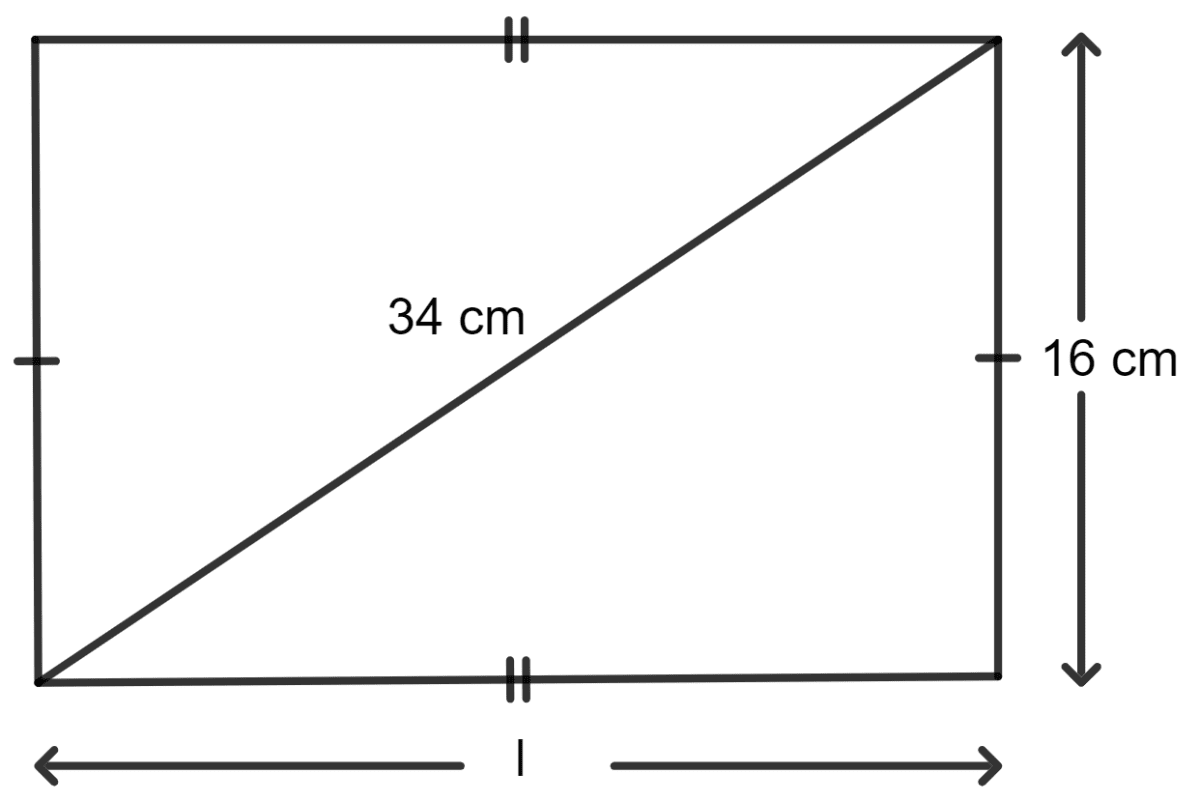
By using Pythagoras theorem,
⇒ Diagonal2 = Length2 + Breadth2
⇒ (34)2 = l2 + (16)2
⇒ 1,156 = l2 + 256
⇒ l2 = 1,156 - 256
⇒ l2 = 900
⇒ l =
⇒ l = 30 cm
Hence, the length of the rectangle is 30 cm.
(ii) As we know, the area of the rectangle = length x breadth
= 30 x 16 cm2
= 480 cm2
Hence, the area of the rectangle is 480 cm2.
The area of a small rectangular plot is 84 m2. If the difference between its length and the breadth is 5 m, find its perimeter.
Answer
Given:
The area of a small rectangular plot is 84 m2.
The difference between its length and the breadth is 5 m.
Let the length of the rectangle be l m.
So, breadth of the rectangle = l - 5
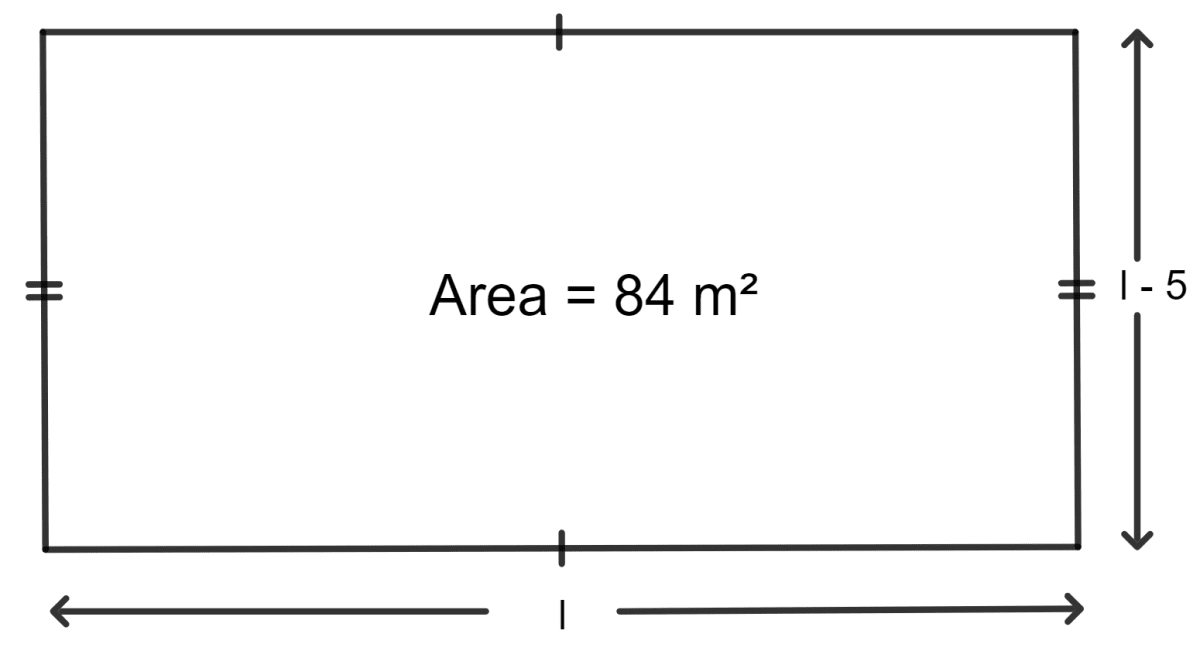
As we know, the area of the rectangle = length x breadth
⇒ l x (l - 5) = 84
⇒ l2 - 5l = 84
⇒ l2 - 5l - 84 = 0
⇒ l2 - (12 - 7)l - 84 = 0
⇒ l2 - 12l + 7l - 84 = 0
⇒ l(l - 12) + 7(l - 12) = 0
⇒ (l - 12)(l + 7) = 0
⇒ l = 12 or - 7
Since length cannot be negative, the length will be 12 m.
So, breadth of the rectangle = (l - 5)
= (12 - 5) m
= 7 m
And, perimeter of the rectangle = 2(length + breadth)
= 2(12 + 7) m
= 2 x 19 m
= 38 m
Hence, the perimeter of the rectangle is 38 m.
The diagonal of a square is 15 m; find the length of its one side and perimeter.
Answer
Given:
Diagonal of the square is 15 m.
Let each side of the square be a m.
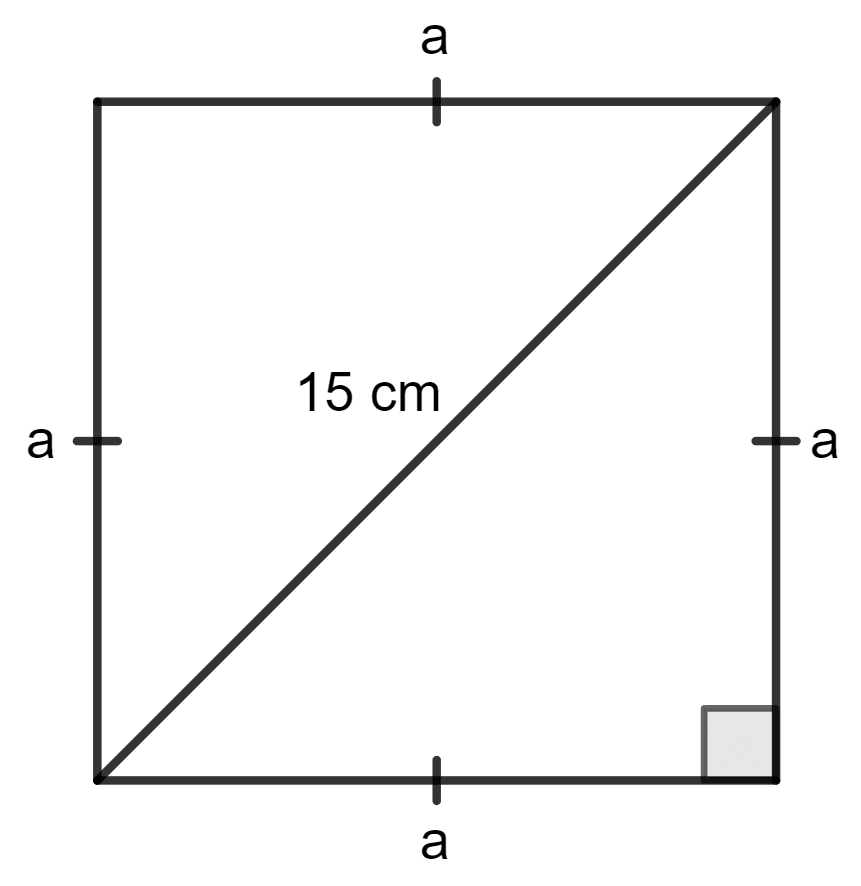
Then, by using Pythagoras theorem,
⇒ Diagonal2 = Side2 + Side2
⇒ (15)2 = a2 + a2
⇒ 225 = 2a2
⇒ a2 =
⇒ a2 = 112.5
⇒ a =
⇒ a = 10.6
As we know that perimeter of the square = 4 x side
= 4 x 10.6 m
= 42.4 m
Hence, the side of square is 10.6 m and its perimeter is 42.4 m.
The length of a rectangle is 16 cm and its perimeter is equal to the perimeter of a square with side 12.5 cm. Find the area of the rectangle.
Answer
Given:
The length of the rectangle is 16 cm.
The perimeter of the rectangle = The perimeter of a square.
The side of the square is 12.5 cm.
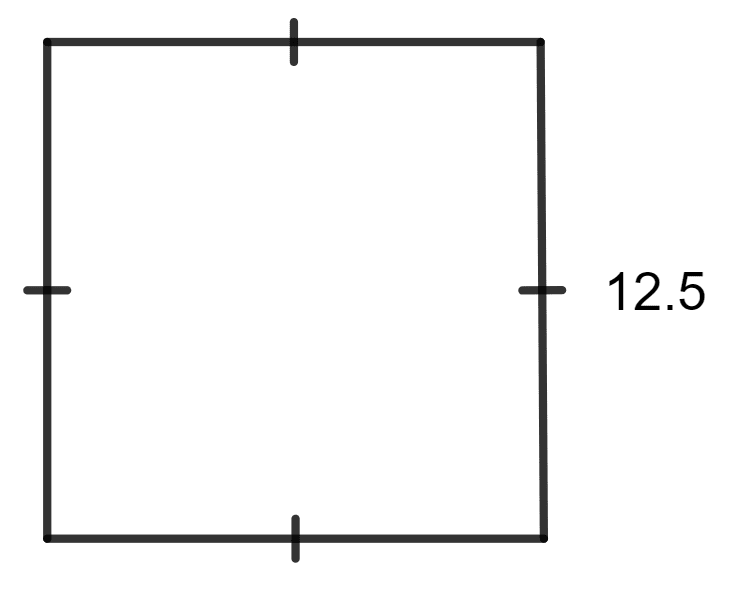
As we know, the perimeter of the square = 4 x side
= 4 x 12.5 cm
= 50 cm
Let the breadth of the rectangle be b cm.
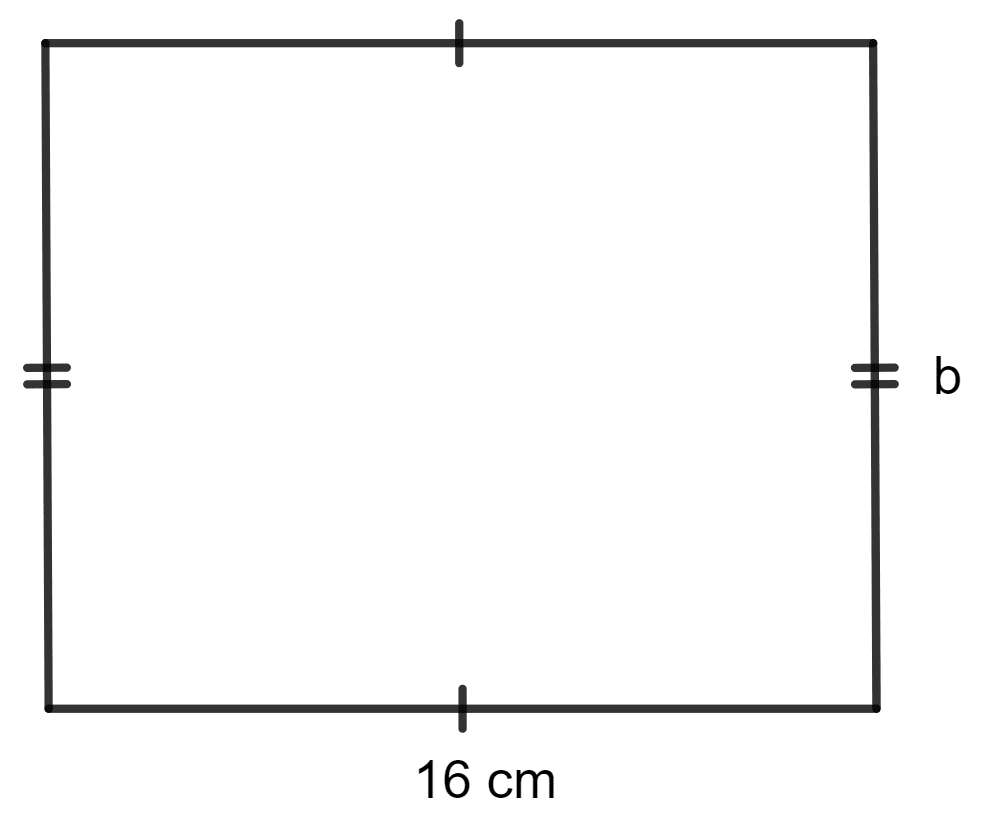
And, the perimeter of the rectangle = 2 (length + breadth)
⇒ 2 (16 + b) = 50
⇒ 16 + b =
⇒ 16 + b = 25
⇒ b = 25 - 16
⇒ b = 9 cm
Now, area of the rectangle = length x breadth
= 16 x 9 cm2
= 144 cm2
Hence, the area of the rectangle is 144 cm2.
The perimeter of a square is numerically equal to its area. Find its area.
Answer
Given:
The perimeter of a square = The area of a square.
Let the side of the square be a unit.
As we know, the perimeter of the square = 4 x side
= 4a
And, the area of the square = side2
= a2
Thus, 4a = a2
⇒ a = 4 unit
Now, the area of the square = a2
= 42
= 16 sq. units
Hence, the area of the square is 16 sq. units.
Each side of a rectangle is doubled. Find the ratio between :
(i) perimeters of the original rectangle and the resulting rectangle
(ii) areas of the original rectangle and the resulting rectangle
Answer
(i) Given:
Each side of a rectangle is doubled.
Let the length and breadth of the rectangle be l and b.
Thus, the new length and breadth of the rectangle are 2l and 2b.
As we know, the perimeter of a rectangle = 2 (length + breadth)
The perimeter of the original rectangle = 2 (l + b)
The perimeter of the new rectangle = 2 (2l + 2b)
= 4 (l + b)
Thus, the ratio of the perimeters of the original rectangle and the resulting rectangle =
=
=
=
Hence, the ratio of the perimeters of the original rectangle and the resulting rectangle is .
(ii) As we know, the area of a rectangle = length x breadth
The area of the original rectangle = l x b
= lb
The area of the new rectangle = 2l x 2b
= 4 lb
Thus, the ratio of the areas of the original rectangle and the resulting rectangle =
=
=
Hence, the ratio of areas of the original rectangle and the resulting rectangle is .
In each of the following cases ABCD is a square and PQRS is a rectangle. Find, in each case, the area of the shaded portion. (All measurements are in metre).
(i)
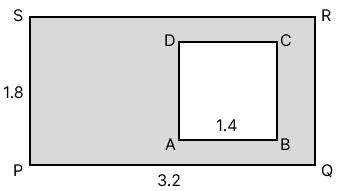
(ii)

Answer
(i) The area of the shaded portion = Area of the rectangle - Area of the square.
It is given that the length and breadth of the rectangle area 3.2 m and 1.8 m.
As we know, the area of the rectangle = length x breadth
= 3.2 x 1.8 m2
= 5.76 m2
The side of the square is 1.4 m.
And, the area of the square = side2
= 1.42 m2
= 1.96 m2
Thus, the area of the shaded portion = 5.76 - 1.96 m2
= 3.8 m2
Hence, the area of the shaded portion is 3.8 m2.
(ii) The area of the shaded portion = Area of the square - Area of the rectangle.
It is given that the side of the square is 6 m.
And, the area of the square = side2
= 62 m2
= 36 m2
The length and breadth of the rectangle are 4.8 m and 3.6 m, respectively.
As we know, the area of the rectangle = length x breadth
= 4.8 x 3.6 m2
= 17.28 m2
Area of the shaded portion = 36 - 17.28 m2
= 18.72 m2
Hence, the area of the shaded portion is 18.72 m2.
A path of uniform width, 3 m, runs around the outside of a square field of side 21 m. Find the area of the path.
Answer
Given:
The side of the square field is 21 m.
The width of the path is 3 m.
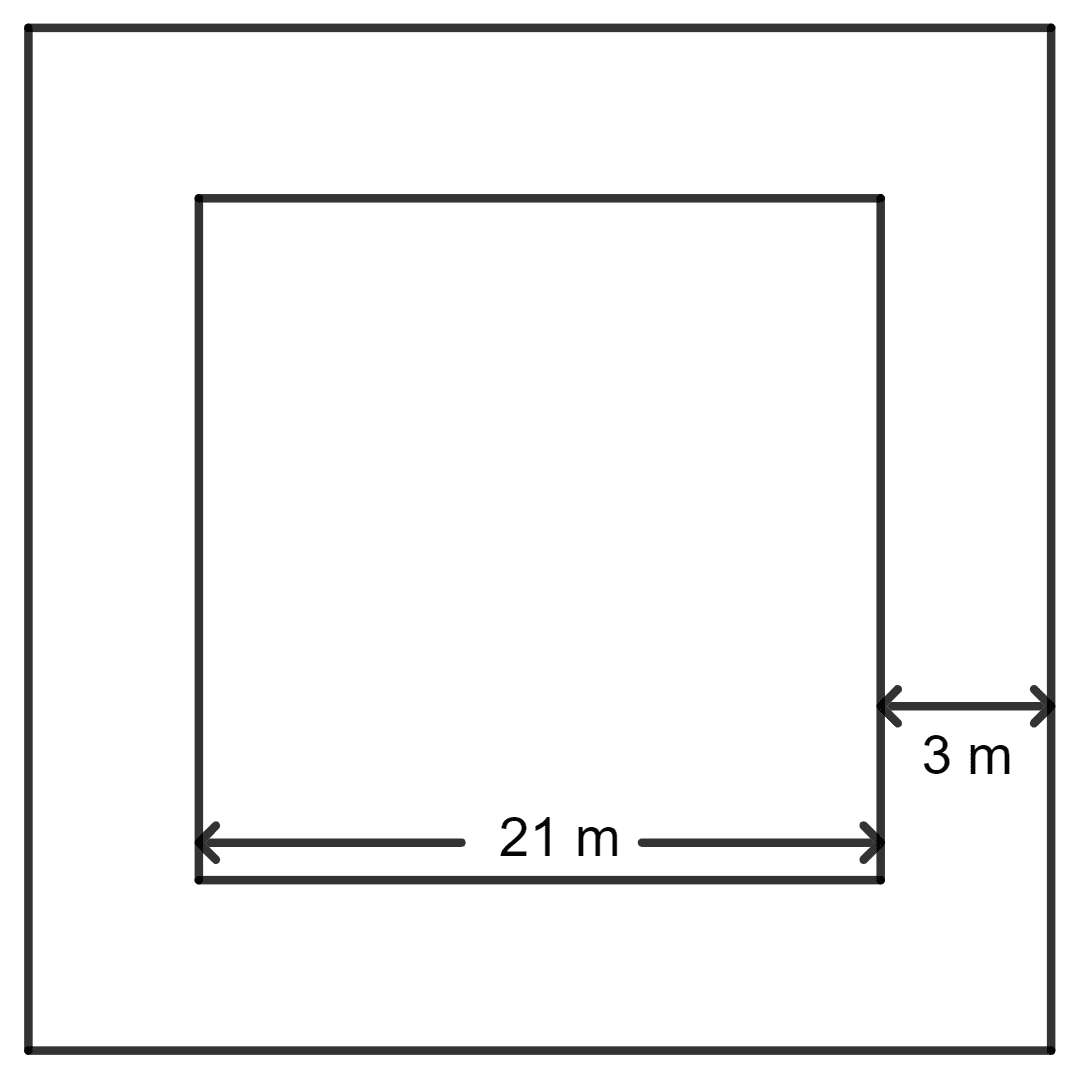
Area of the path = Area of bigger square field - Area of smaller square field
The side of the bigger square = 21 m + 3 m + 3m
= 27 m
As we know, the area of square = side2
⇒ Area of the bigger square = 272 m2
= 729 m2
⇒ Area of the smaller square = 212 m2
= 441 m2
So, the area of the path = 729 - 441 m2
= 288 m2
Hence, the area of the path is 288 m2.
A path of uniform width, 2.5 m, runs around the inside of a rectangular field 30 m by 27 m. Find the area of the path.
Answer
Given:
The length of the rectangular field is 30 m.
The breadth of the rectangular field is 27 m.
The width of the path is 2.5 m.
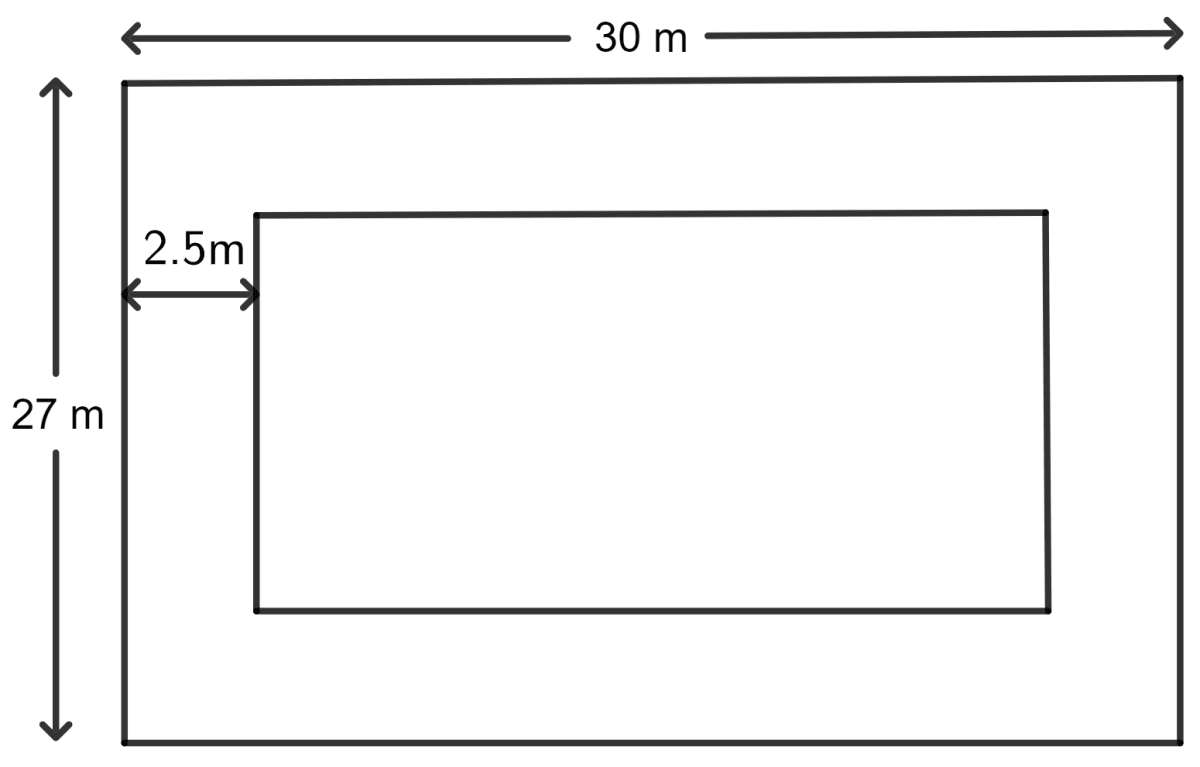
Area of the path = Area of bigger rectangular field - Area of smaller rectangular field
The length of the smaller rectangular field = 30 m - 2.5 m - 2.5 m
= 25 m
The breadth of the smaller rectangular field = 27 m - 2.5 m - 2.5 m
= 22 m
As we know, the area of a rectangle = length x breadth
⇒ Area of the bigger rectangular field = 30 x 27 m2
= 810 m2
⇒ Area of the smaller square = 25 x 22 m2
= 550 m2
So, the area of the path = 810 - 550 m2
= 260 m2
Hence, the area of the path is 260 m2.
The length of a hall is 18 m and its width is 13.5 m. Find the least number of square tiles, each of side 25 cm, required to cover the floor of the hall,
(i) without leaving any margin.
(ii) leaving a margin of width 1.5 m all around.
In each case, find the cost of the tiles required at the rate of ₹ 6 per tile.
Answer
(i) Given:
Length of the floor = 18 m
Breadth of the floor = 13.5 m
As we know, the area of the floor = length x breadth
= 18 x 13.5 m2
= 243 m2
Side of the square tile = 25 cm
= m
= m
As we know, the area of a tile = side2
= 2 m2
= m2
Area of square tiles x Number of tiles = Area of the floor
⇒ Number of tiles =
⇒ Number of tiles =
⇒ Number of tiles = 243 x 16
⇒ Number of tiles = 3,888
Rate per tile = ₹ 6 per tile
Total cost = ₹ 3,888 x 6
= ₹ 23,328
Hence, the number of tiles is 3,888 and the cost of the tiles is ₹ 23,328.
(ii) Width of the margin on each side = 1.5 m
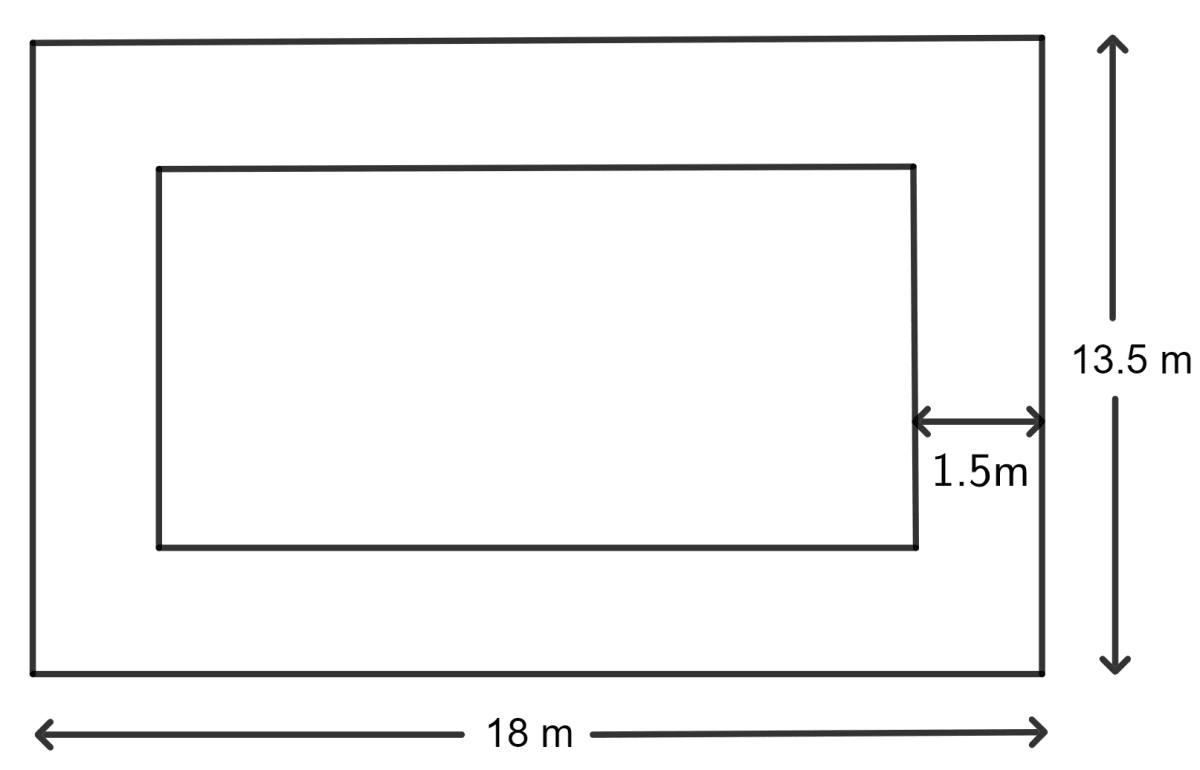
Length of the inner floor = 18 m - 1.5 m - 1.5 m
= 18 - 3 m
= 15 m
Breadth of the inner floor = 13.5 m - 1.5 m - 1.5 m
= 13.5 - 3 m
= 10.5 m
As we know, the area of the floor = length x breadth
= 15 x 10.5 m2
= 157.5 m2
Side of the square tile = 25 cm
= m
= m
As we know, the area of a tile = side2
= 2 m2
= m2
Area of square tiles x Number of tiles = Area of the floor
⇒ Number of tiles =
⇒ Number of tiles =
⇒ Number of tiles = 157.5 x 16
⇒ Number of tiles = 2,520
Rate of tiles = ₹ 6 per tile
Total cost = ₹ 2,520 x 6
= ₹ 15,120
Hence, the number of tiles is 2,520 and the cost of the tiles is ₹ 15,120.
A rectangular field is 30 m in length and 22 m in width. Two mutually perpendicular roads, each 2.5 m wide, are drawn inside the field so that one road is parallel to the length of the field and the other road is parallel to its width. Calculate the area of the crossroads.
Answer
Given:
Length of the rectangular field = 30 m
Width of the rectangular field = 22 m
Width of each road = 2.5 m
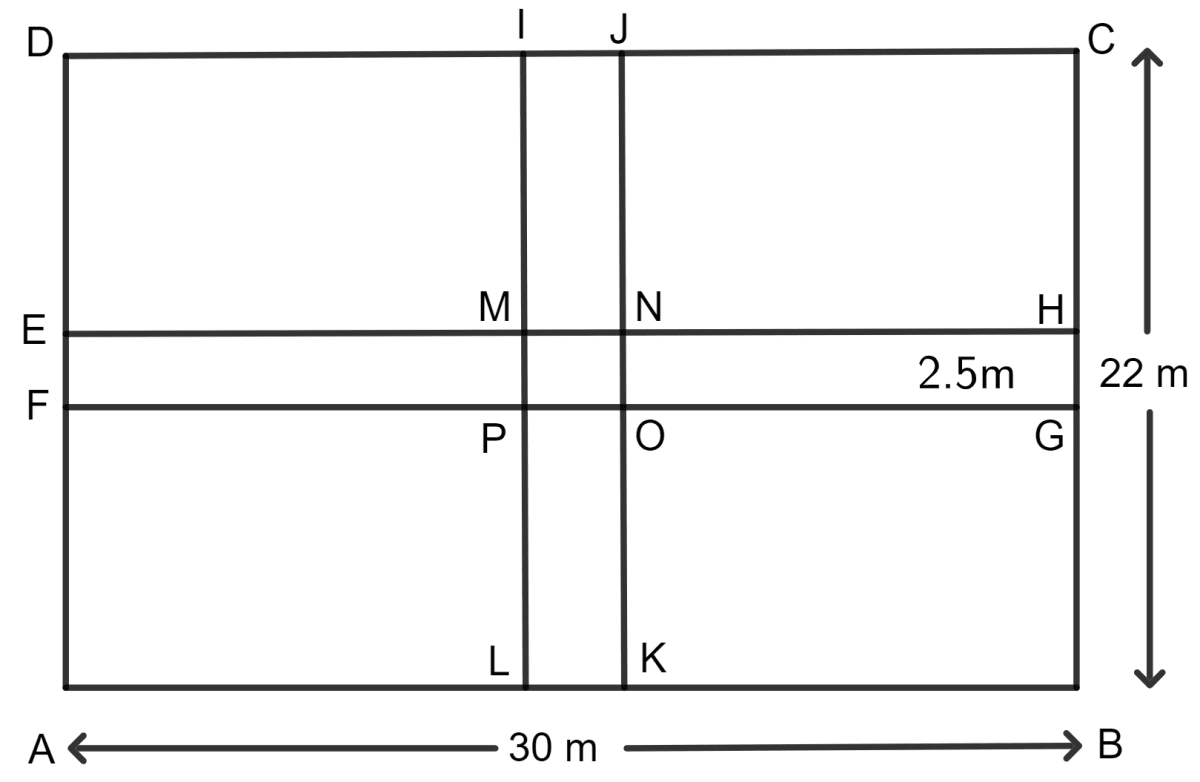
Area of crossroad IJKL (parallel to the width of field) = 2.5 x 22 m2
= 55 m2
Area of crossroad EFGH (parallel to the length of field) = 2.5 x 30 m2
= 75 m2
Side of the square MNOP = 2.5
As we know, the area of the square = side2
Area of the square field MNOP (area common to both roads) = 2.52 m2
= 6.25 m2
Now, area of crossroad = Area of cross road EFGH + Area of cross road IJKL - Area of square field MNOP
= 75 m2 + 55 m2 - 6.25 m2
= 130 m2 - 6.25 m2
= 123.75 m2
Hence, the area of the crossroads is 123.75 m2.
The length and the breadth of a rectangular field are in the ratio 5 : 4 and its area is 3380 m2. Find the cost of fencing it at the rate of ₹ 75 per m.
Answer
Given:
The length and the breadth of a rectangular field are in the ratio 5 : 4.
The area of the rectangular field = 3380 m2
Rate of fencing = ₹ 75 per meter
Let the length of the rectangular field be 5a and the breadth be 4a.
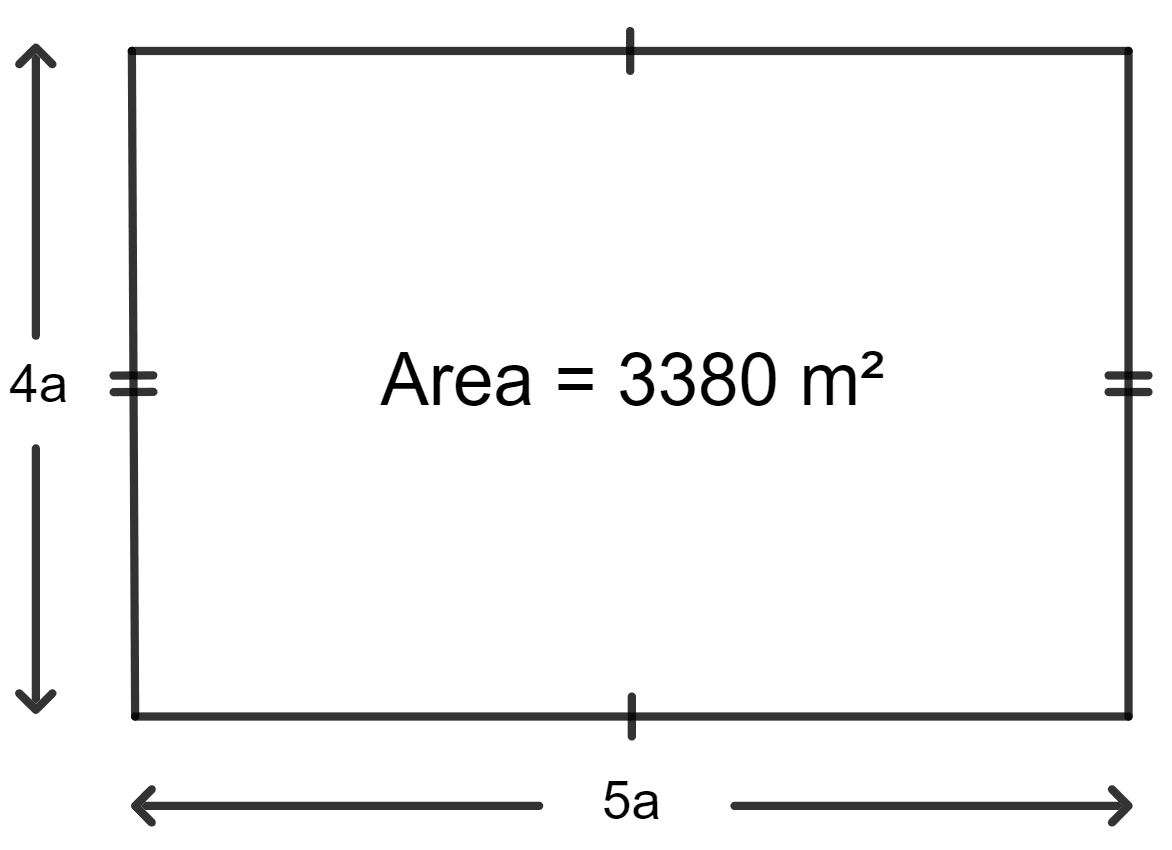
As we know, the area of the rectangle = length x breadth
⇒ 5a x 4a = 3380 m2
⇒ 20a2 = 3380 m2
⇒ a2 = m2
⇒ a2 = 169 m2
⇒ a = m
⇒ a = 13 m
So, the length of the rectangular field = 5a
= 5 x 13 m
= 65 m
And, the breadth of the rectangular field = 4a.
= 4 x 13 m
= 52 m
Perimeter of the rectangle = 2(l + b)
= 2(65 + 52)
= 2 x 117
= 234 m
Total cost of fencing = Rate of fencing x Perimeter of fencing
= ₹ 75 x 234
= ₹ 17,550
Hence, the cost of fencing is ₹ 17,550.
The length and the breadth of a conference hall are in the ratio 7 : 4 and its perimeter is 110 m. Find :
(i) area of the floor of the hall.
(ii) number of tiles, each a rectangle of size 25 cm x 20 cm, required for flooring of the hall.
(iii) the cost of the tiles at the rate of ₹ 1,400 per hundred tiles.
Answer
(i) Given:
The length and the breadth of a conference hall are in the ratio 7 : 4.
The perimeter of the hall = 110 m
Let the length of the conference hall be 7a and the breadth be 4a.
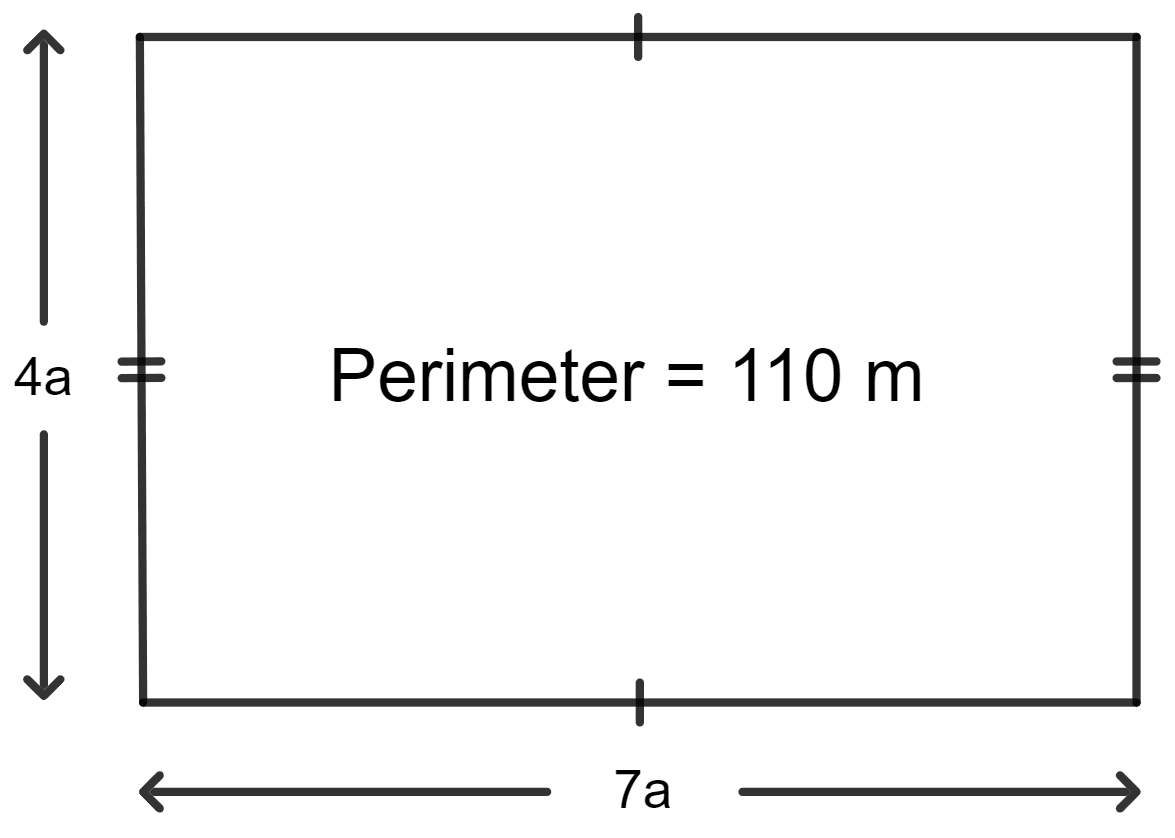
As we know, the perimeter of the hall = 2(length + breadth)
⇒ 2(7a + 4a) = 110
⇒ 2 x 11a = 110
⇒ 22a = 110
⇒ a =
⇒ a = 5
So, the length of the hall = 7a
= 7 x 5 m
= 35 m
And, the breadth of the hall = 4a
= 4 x 5 m
= 20 m
Area of the hall = length x breadth
= 35 x 20 m2
= 700 m2
Hence, the area of the conference hall is 700 m2.
(ii) Given:
Length of the tile = 25 cm
= m
= m
Breadth of the tile = 20 cm
= m
= m
Area of the tile = length x breadth
= m2
= m2
Area of hall = Area of tiles x Number of tiles
⇒ 700 = x Number of tiles
⇒ Number of tiles = 700 x 20
⇒ Number of tiles = 14,000
Hence, the number of tiles = 14,000.
(iii) Cost of tiles = ₹ 1,400 per 100 tiles
Total cost =
= ₹ 1,96,000
Hence, the cost of tiles = ₹ 1,96,000.
The parallel sides of a trapezium are 12 cm and 10 cm. If the distance between the parallel sides is 10 cm; the area of the trapezium is :
220 cm2
110 cm2
55 cm2
165 cm2
Answer
Given:
The lengths of the parallel sides of the trapezium are 12 cm and 10 cm.
The distance between the parallel sides is 10 cm.
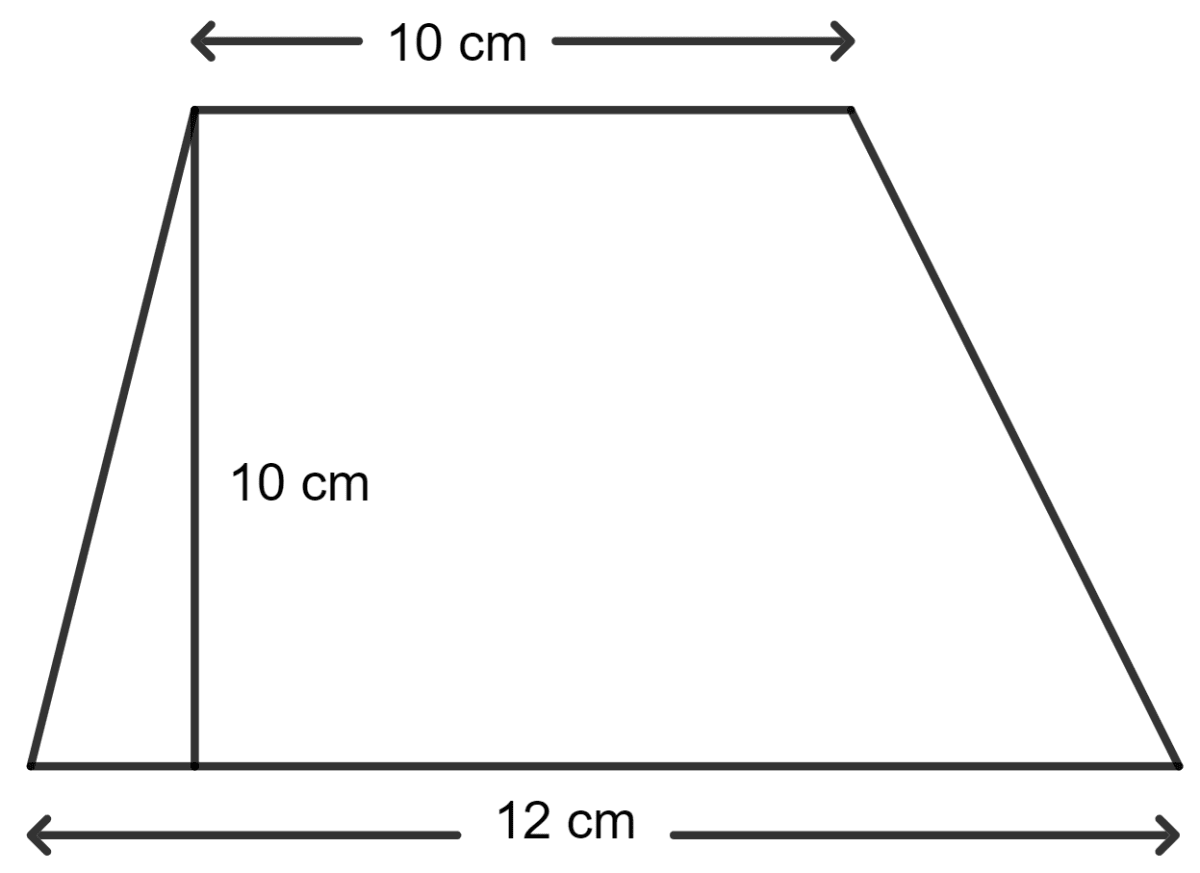
As we know, the area of a trapezium = x (sum of parallel sides) x height
= x (12 + 10) x 10 cm2
= x 22 x 10 cm2
= x 220 cm2
= 110 cm2
Hence, option 2 is the correct option.
Two parallel sides of a trapezium are in the ratio 2 : 3 and the distance between them is 12 cm. If the area of the trapezium is 240 cm2; the length of its larger parallel side is :
16 cm
20 cm
24 cm
32 cm
Answer
Given:
Two parallel sides of a trapezium are in the ratio 2 : 3.
The distance between the parallel sides = 12 cm.
The area of the trapezium = 240 cm2.
Let the parallel sides of a trapezium be 2a and 3a.
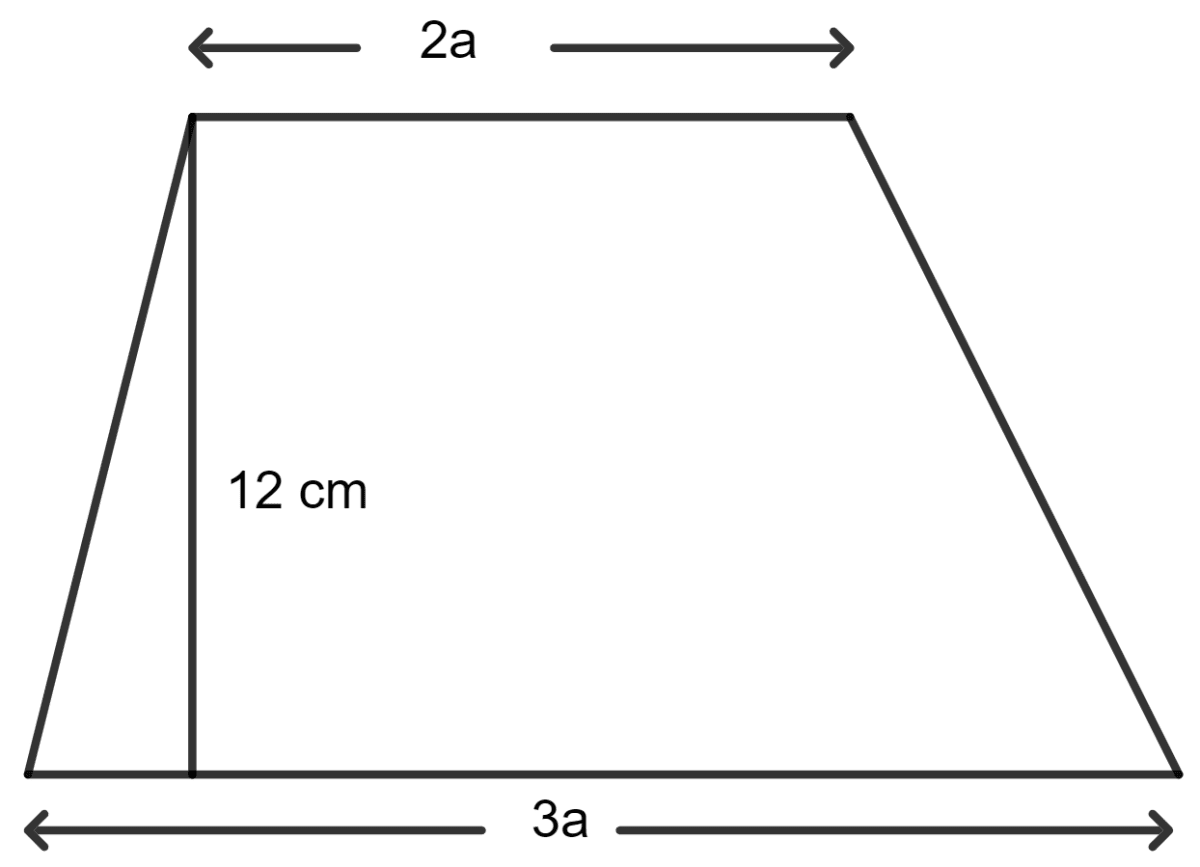
As we know, the area of a trapezium = x (sum of parallel sides) x height
⇒ x (2a + 3a) x 12 cm2 = 240 cm2
⇒ x 5a x 12 = 240
⇒ x 60a = 240
⇒ 30a = 240
⇒ a =
⇒ a = 8
So, the length of its larger parallel side = 3a
= 3 x 8 cm
= 24 cm
Hence, option 3 is the correct option.
The adjacent sides of a parallelogram are 12 cm and 9 cm. The distance between longer sides is 6 cm; the distance between shorter sides is :
12 cm
9 cm
8 cm
6 cm
Answer
Given:
The base of the parallelogram = 12 cm.
The height of the parallelogram = 6 cm.
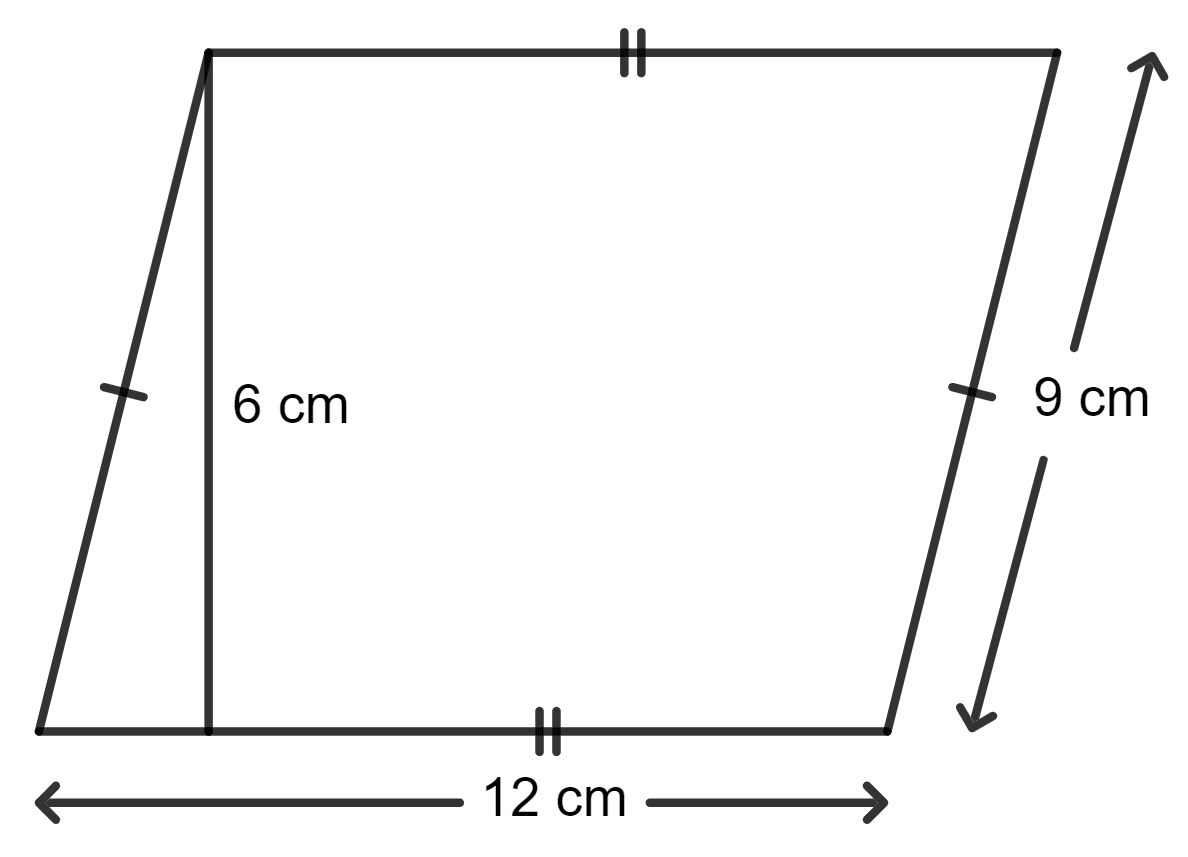
As we know, the area of parallelogram = base x height
The area of the parallelogram using the longer side:
= 12 x 6 cm2
= 72 cm2
The base of the parallelogram = 9 cm.
Let the height of the parallelogram be b cm.
The area of the parallelogram using the shorter side:
= 9 x b cm2
Since the area is the same, we can equate both areas:
⇒ 9 x b cm2 = 72 cm2
⇒ b = cm
⇒ b = 8 cm
Hence, option 3 is the correct option.
Each side of a rhombus is 9 cm and the distance between its opposite sides is 6 cm. The area of the rhombus is :
54 cm2
108 cm2
27 cm2
13.5 cm2
Answer
Given:
The base of the rhombus = 9 cm.
The height of the rhombus = 6 cm.
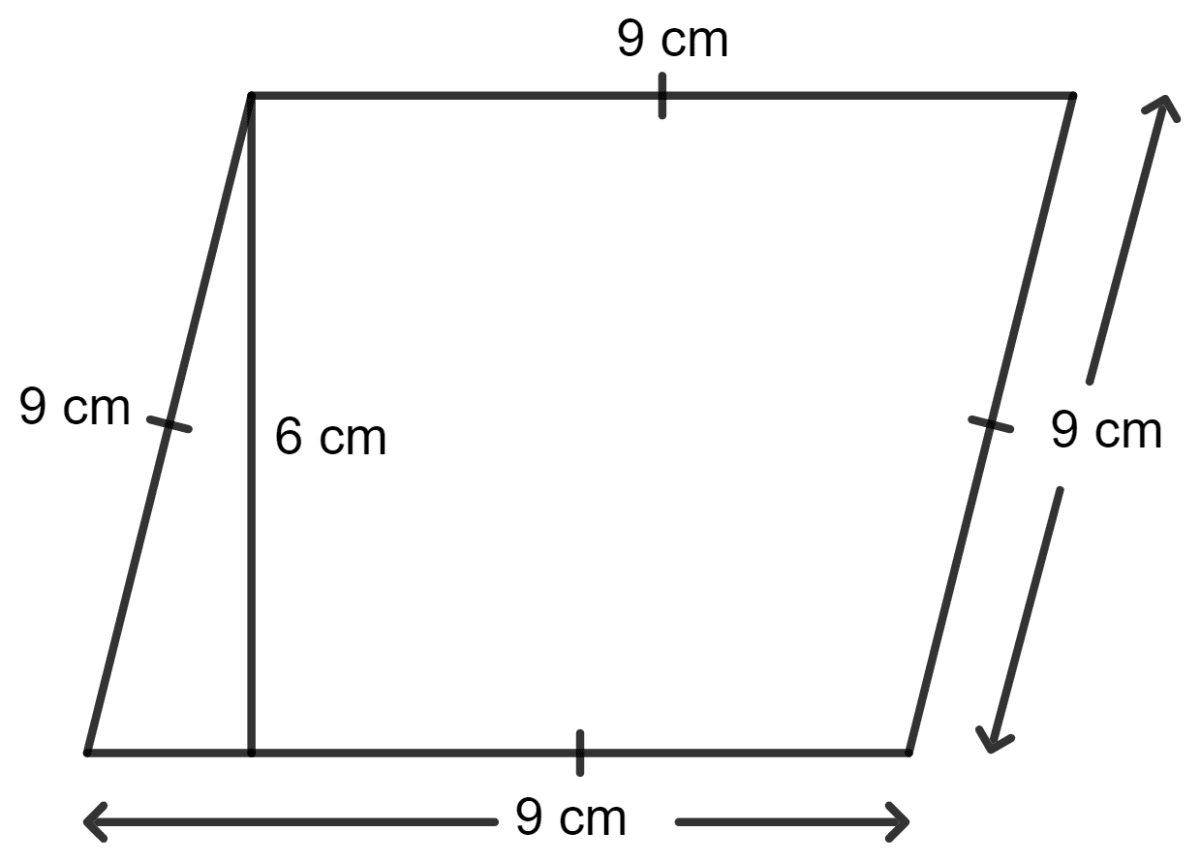
As we know, the area of a rhombus = base x height
= 9 x 6 cm2
= 54 cm2
Hence, option 1 is the correct option.
The diagonal of a rhombus is 15 cm and its area is 60 cm2; the other diagonal of the rhombus is :
4 cm
8 cm
12 cm
16 cm
Answer
Given:
The diagonal of a rhombus = 15 cm.
The area = 60 cm2
Let the other diagonal of the rhombus be d.
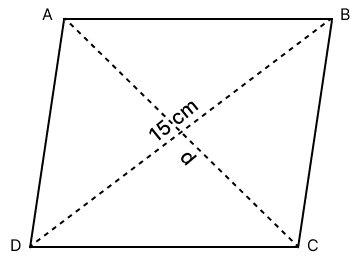
As we know, the area of a rhombus = x product of its diagonals
⇒ x (15 x d) = 60
⇒ x d = 60
⇒ d = cm
⇒ d = cm
⇒ d = 8 cm
Hence, option 2 is the correct option.
The following figure shows the cross-section ABCD of a swimming pool which is a trapezium in shape.
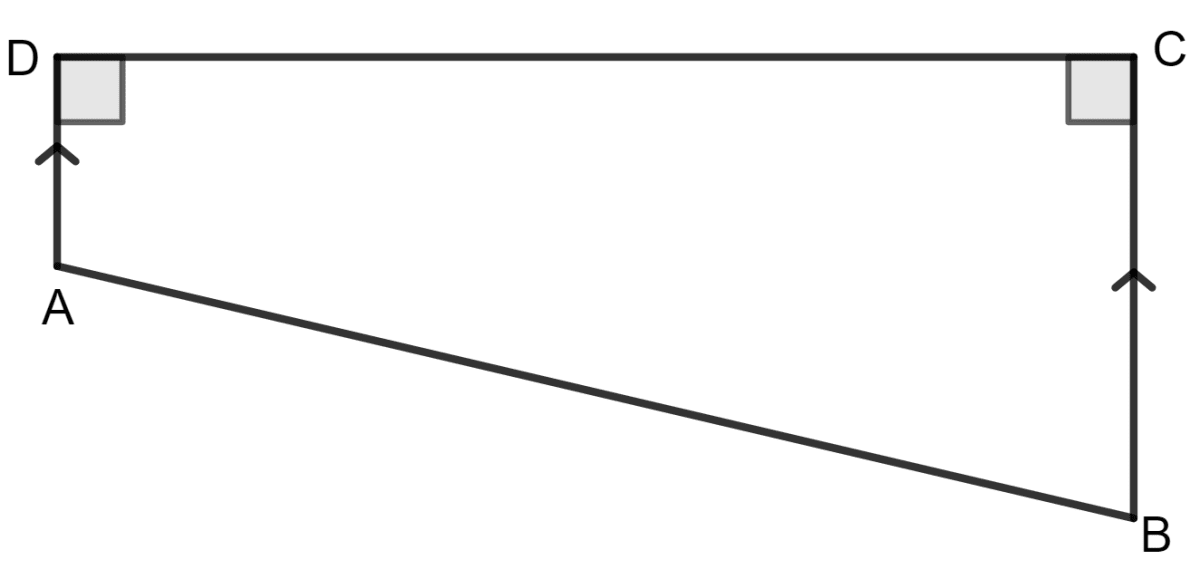
If the width DC of the swimming pool is 6.4 m, depth (AD) at the shallow end is 80 cm and depth (BC) at the deepest end is 2.4 m, find its area of cross-section.
Answer
Given:
DC = 6.4 m
AD = 80 cm = m = 0.8 m
BC = 2.4 m
Area of the cross-section = Area of trapezium ABCD
= x (sum of parallel sides) x height
= x (0.8 + 2.4) x 6.4
= x 3.2 x 6.4
= x 20.48
= 10.24 m2
Hence, the area of cross-section is 10.24 m2.
The parallel sides of a trapezium are in the ratio 3 : 4. If the distance between the parallel sides is 9 dm and its area is 126 dm2, find the lengths of its parallel sides.
Answer
Given:
The parallel sides of a trapezium are in the ratio 3 : 4.
The distance between the parallel sides = 9 dm
The area = 126 dm2
Let the parallel sides of trapezium be 3a and 4a.
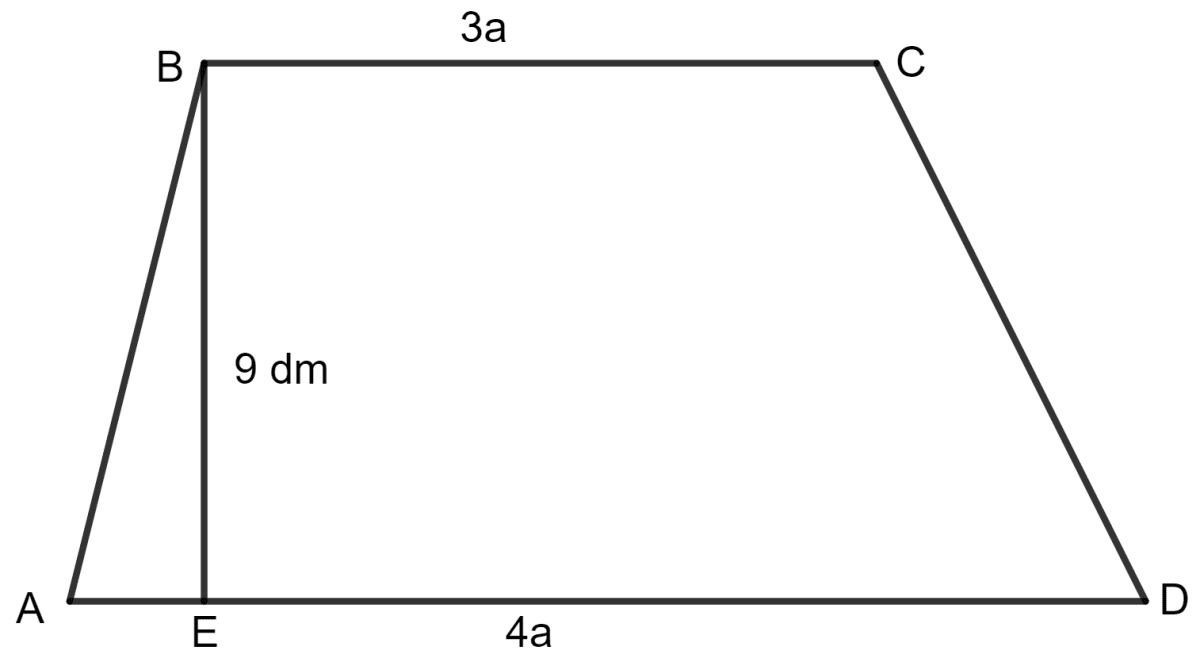
As we know, the area of a trapezium = x (sum of parallel side) x height
⇒ x (3a + 4a) x 9 = 126
⇒ x 7a x 9 = 126
⇒ x 63a = 126
⇒ 63a = 126 x 2
⇒ 63a = 252
⇒ a =
⇒ a = 4
So, the parallel sides of the trapezium are:
For 3a:
= 3 x 4 dm = 12 dm
And, for 4a:
= 4 x 4 dm = 16 dm
Hence, the lengths of its parallel sides are 12 dm and 16 dm.
The two parallel sides and the distance between them are in the ratio 3 : 4 : 2. If the area of the trapezium is 175 cm2, find its height.
Answer
Given:
The two parallel sides and the distance between them are in the ratio 3 : 4 : 2.
The area of the trapezium is 175 cm2.
So, the two parallel sides of the trapezium are 3a and 4a.
Distance between them is 2a.
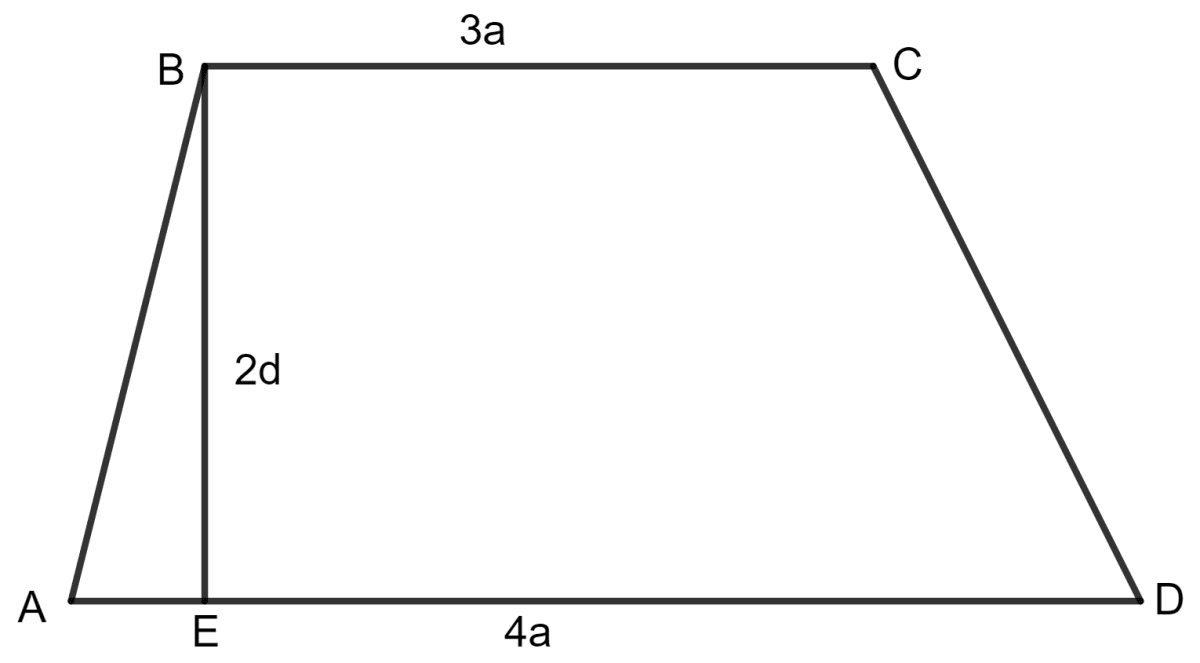
As we know, the area of a trapezium = x (sum of parallel side) x height
⇒ x (3a + 4a) x 2a = 175
⇒ x 7a x 2a = 175
⇒ x 14a2 = 175
⇒ 7a2 = 175
⇒ a2 =
⇒ a2 = 25
⇒ a =
⇒ a = 5
So, height of the trapezium = 2a
= 2 x 5 cm
= 10 cm
Hence, the height of the trapezium is 10 cm.
The adjacent sides of a parallelogram are 21 cm and 28 cm. If its one diagonal is 35 cm, find the area of the parallelogram.
Answer
Let the parallelogram be ABCD as shown in the figure below:
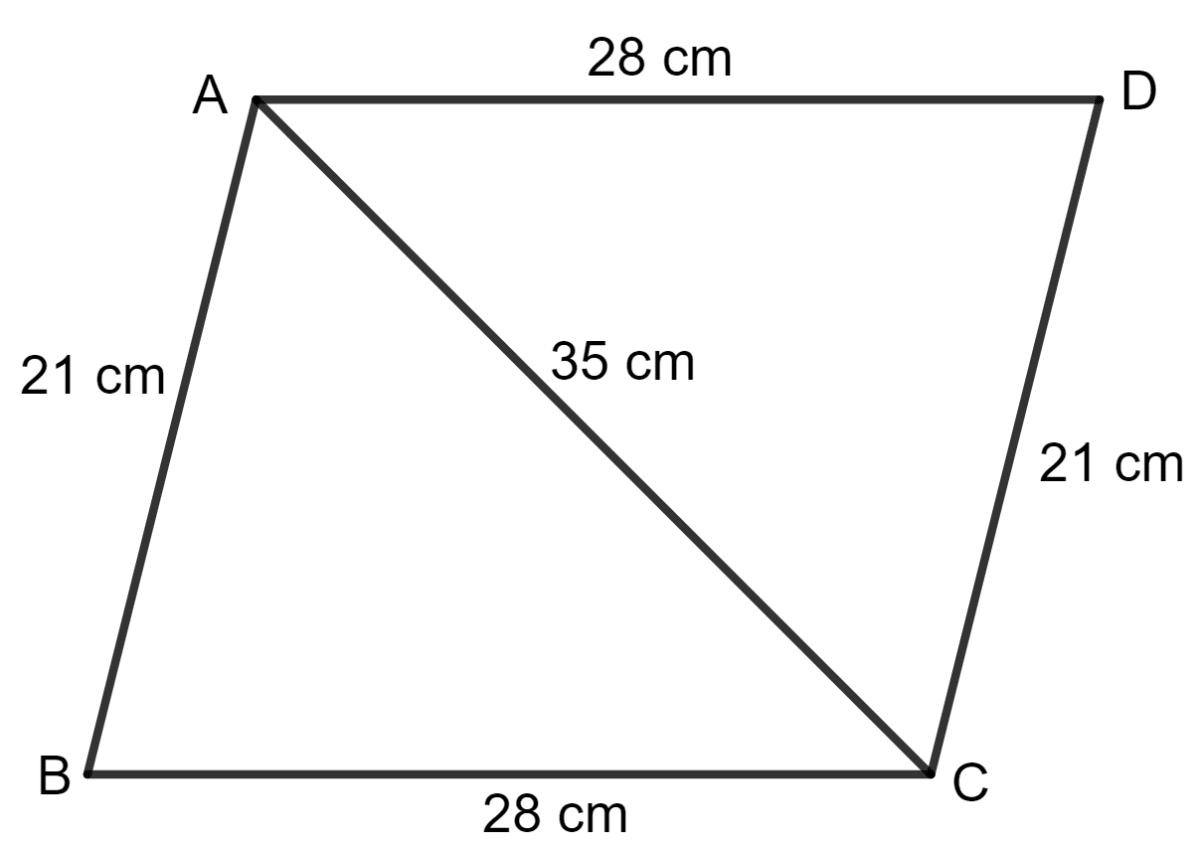
For triangle ABC,
AB = 21 cm, BC = 28 cm and AC = 35 cm.
∵ Area of triangle ABC =
= cm2
= cm2
= cm2
= 294 cm2
∵ Diagonal of parallelogram divides it into two equal parts.
So, area of parallelogram ABCD = 2 x area of triangle ABC.
= 2 x 294 cm2
= 588 cm2
Hence, the area of the parallelogram is 588 cm2.
The diagonals of a rhombus are 18 cm and 24 cm. Find :
(i) its area
(ii) length of its sides
(iii) its perimeter
Answer
(i) Given:
The diagonals of a rhombus are 18 cm and 24 cm.
As we know, the area of rhombus = x product of its diagonal
= x 18 x 24 cm2
= x 432 cm2
= 216 cm2
Hence, the area of the rhombus is 216 cm2.
(ii) AC = 18 cm
Then, OA = OC = = 9 cm
And, BD = 24 cm
Then, OB = OD = = 12 cm
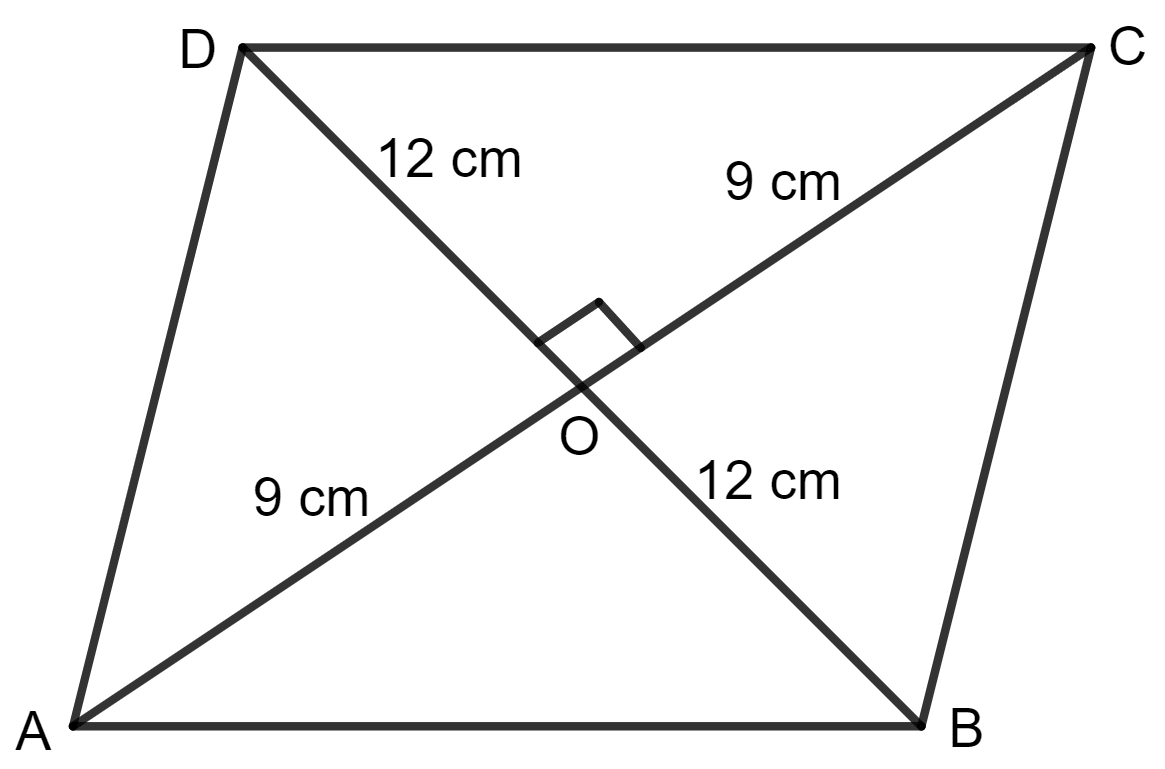
Since the diagonals of a rhombus bisect at 90°.
Applying pythagoras theorem in triangle AOB, we get:
AB2 = OA2 + OB2
⇒ AB2 = (9)2 + (12)2
⇒ AB2 = 81 + 144
⇒ AB2 = 225
⇒ AB =
⇒ AB = 15 cm
Hence, the length of each side of the rhombus is 15 cm.
(iii) As we know, the perimeter of the rhombus = 4 x side
= 4 x 15 cm
= 60 cm
Hence, the perimeter of the rhombus is 60 cm.
The perimeter of a rhombus is 40 cm. If one diagonal is 16 cm, find :
(i) its other diagonal
(ii) its area
Answer
(i) Given:
The perimeter of a rhombus = 40 cm.
One diagonal = 16 cm.
As we know, the perimeter of the rhombus = 4 x side
⇒ 4 x side = 40 cm
⇒ Side = cm
⇒ Side = 10 cm
AB = 10 cm
AC = 16 cm
Then, OA = OC = = 8 cm
Let OB be a cm.
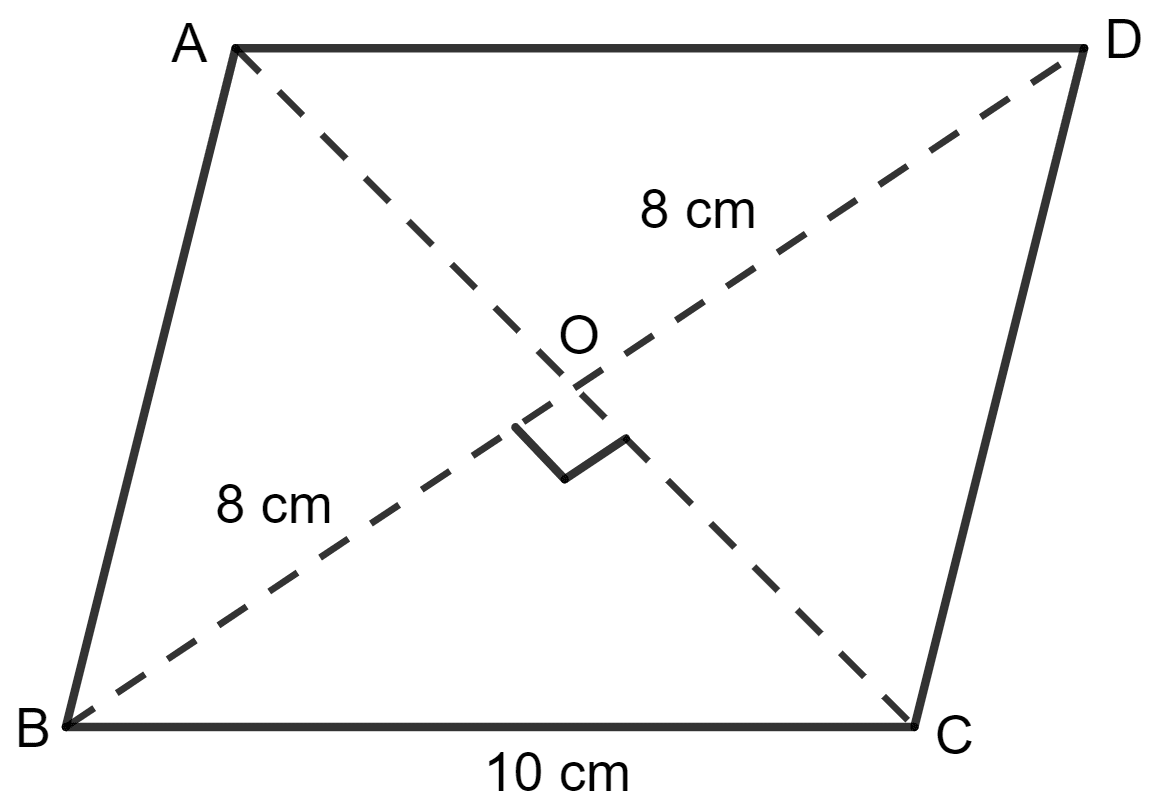
Since the diagonal of a rhombus bisect at 90°.
Applying pythagoras theorem in triangle AOB, we get:
AB2 = OA2 + OB2
⇒ (10)2 = (8)2 + a2
⇒ 100 = 64 + a2
⇒ a2 = 100 - 64
⇒ a2 = 36
⇒ a =
⇒ a = 6
So, OB = 6 cm
BD = 2 x 6 cm
= 12 cm
Hence, the length of other diagonal is 12 cm.
(ii) As we know that area of rhombus = x product of its diagonal
= x 16 x 12 cm2
= x 192 cm2
= 96 cm2
Hence, the area of the rhombus is 96 cm2.
The length of the diagonals of a rhombus is in the ratio 4 : 3. If its area is 384 cm2, find its side.
Answer
Given:
The length of the diagonals of a rhombus is in the ratio 4 : 3.
The area = 384 cm2
Let the length of the diagonals be 4a and 3a.
As we know, the area of rhombus = x product of its diagonal
⇒ x 4a x 3a = 384
⇒ x 12a2 = 384
⇒ 6a2 = 384
⇒ a2 =
⇒ a2 = 64
⇒ a =
⇒ a = 8
The length of the diagonals be 4a and 3a.
= 4 x 8 cm and 3 x 8 cm
= 32 cm and 24 cm
AC = 32 cm
Then, OA = OC = = 16 cm
And, BD = 24 cm
Then, OB = OD = = 12 cm
Since the diagonal of a rhombus bisect at 90°.
Applying pythagoras theorem in ΔAOB, we get:
AB2 = OA2 + OB2
⇒ AB2 = (16)2 + (12)2
⇒ AB2 = 256 + 144
⇒ AB2 = 400
⇒ AB =
⇒ AB = 20 cm
Hence, the length of its side is 20 cm.
A thin metal iron-sheet is a rhombus in shape, with each side 10 m. If one of its diagonals is 16 m, find the cost of painting its both sides at the rate of ₹ 6 per m2.
Also, find the distance between the opposite sides of this rhombus.
Answer
Given:
Side of iron sheet (AB) = 10 m
Diagonal of the sheet (AC) = 16 m
Join BD.
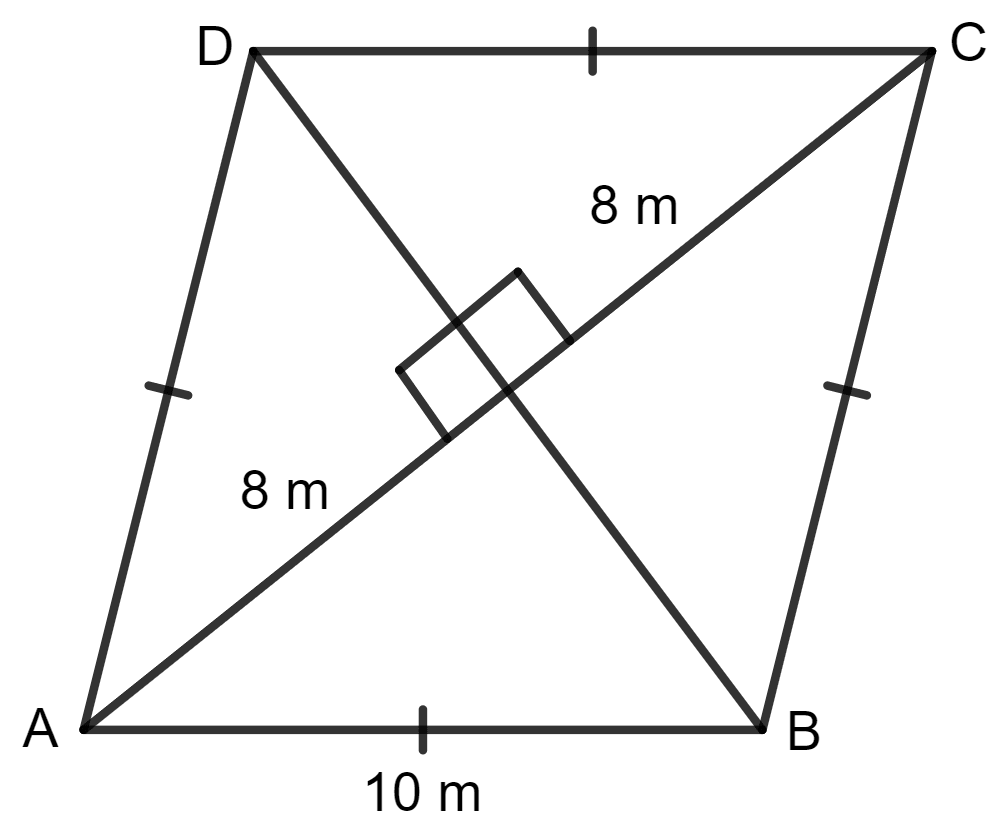
Then, OA = OC = = = 8 m
Since the diagonals of a rhombus bisect each other at 90°, applying the pythagoras theorem in Δ AOB, we get:
AB2 = OA2 + OB2
⇒ (10)2 = (8)2 + OB2
⇒ 100 = 64 + OB2
⇒ OB2 = 100 - 64
⇒ OB2 = 36
⇒ OB =
⇒ OB = 6 m
Thus, BD = 2 x OB = 2 x 6 m = 12 m
The area of rhombus = x product of diagonals
= x 16 x 12 m2
= x 192 m2
= 96 m2
The rate of painting is ₹ 6 per m2.
Therefore, the total cost of painting is:
Total cost = 2 x area of sheet x rate of painting
= 2 x 96 x 6
= 192 x 6
= ₹ 1,152
We also know that the area of the rhombus = base x height
⇒ 96 = 10 x height
⇒ height =
⇒ height = 9.6 m
Hence, the total cost of painting is ₹ 1,152 and the distance between the opposite sides of the rhombus is 9.6 m.
The area of a trapezium is 279 sq. cm and the distance between its two parallel sides is 18 cm. If one of its parallel sides is longer than the other side by 5 cm, find the lengths of its parallel sides.
Answer
Given:
The area of a trapezium = 279 sq. cm
The distance between its two parallel sides = 18 cm.
One of the parallel sides is longer than the other side by 5 cm.
Let one of the parallel sides be a. Then, the other parallel side is a - 5.
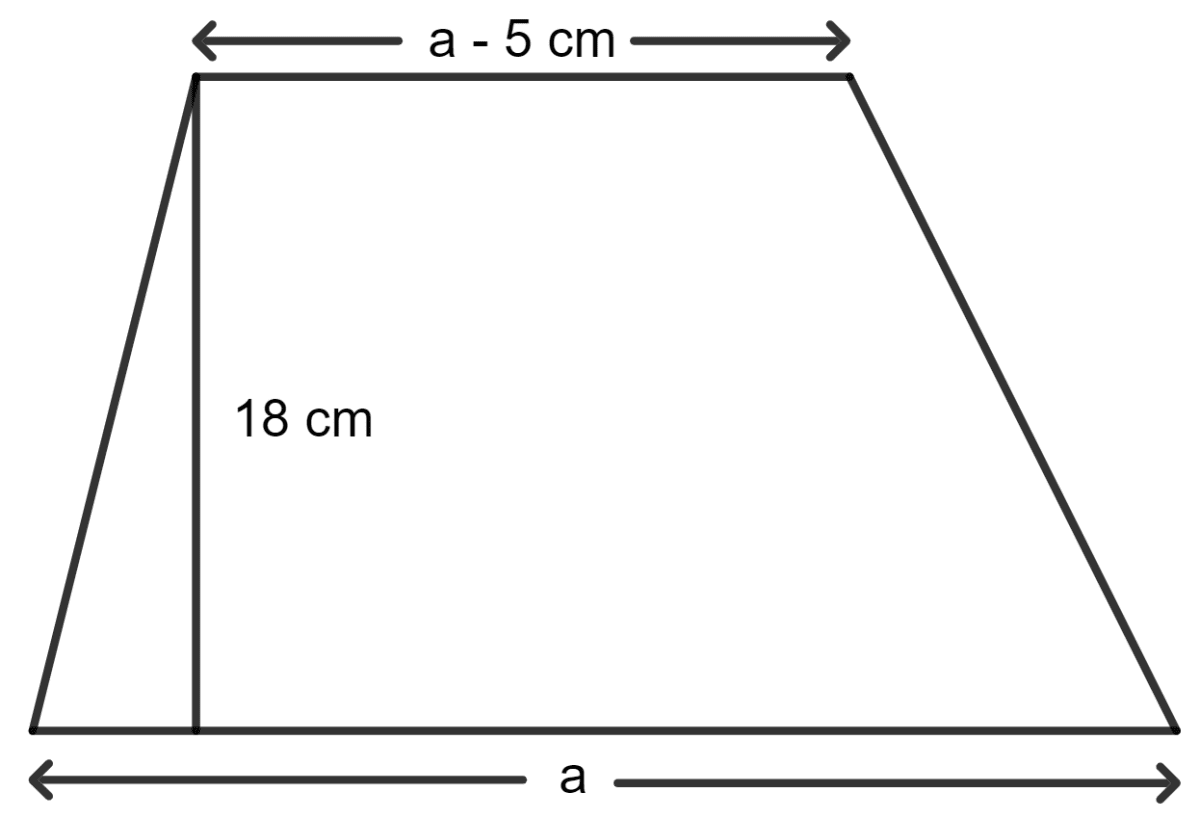
As we know, the area of a trapezium = (sum of parallel sides) x distance between the parallel sides
Substituting the given values:
⇒ 279 = (a + a - 5) x 18
⇒ 279 = (2a - 5) x 18
⇒ 279 = (36a - 90)
⇒ 279 = 18a - 45
⇒ 18a = 279 + 45
⇒ 18a = 324
⇒ a =
⇒ a = 18 cm
So, the parallel sides are 18 cm and (18 - 5) = 13 cm.
Hence, the lengths of the parallel sides are 18 cm and 13 cm, respectively.
The area of a rhombus is equal to the area of a triangle. If base of triangle is 24 cm, its corresponding altitude is 16 cm and one of the diagonals of the rhombus is 19.2 cm, find its other diagonal.
Answer
Given:
The area of a rhombus = The area of a triangle
The base of the triangle = 24 cm
The altitude of the triangle = 16 cm
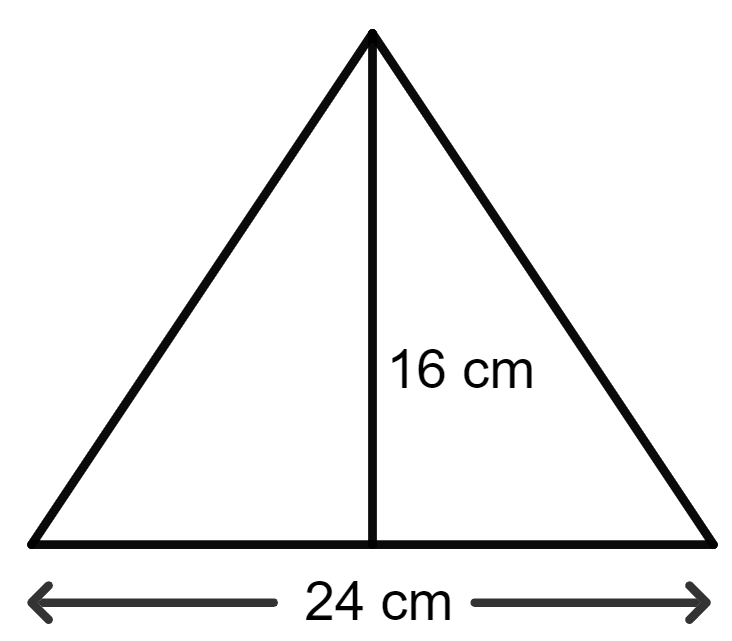
One of the diagonals of the rhombus = 19.2 cm
As we know, the area of a triangle = x base x altitude
= x 24 x 16 cm2
= x 384 cm2
= 192 cm2
Let the length of the other diagonal of the rhombus be d.
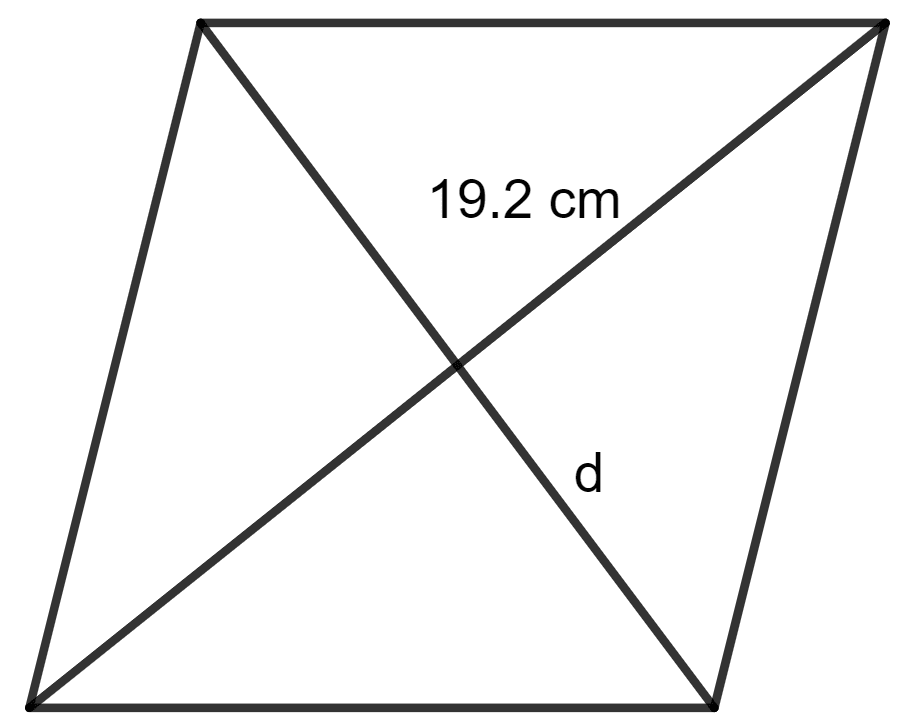
The area of the rhombus = x (product of diagonals)
⇒ x (19.2 x d) = 192
⇒ 9.6 x d = 192
⇒ d =
⇒ d = 20 cm
Hence, the length of the other diagonal is 20 cm.
Find the area of the trapezium ABCD in which AB//DC, AB = 18 cm, ∠B = ∠C = 90°, CD = 12 cm and AD = 10 cm.
Answer
Given:
AB = 18 cm
∠B = ∠C = 90°
CD = 12 cm
AD = 10 cm
Draw DL perpendicular to AB.
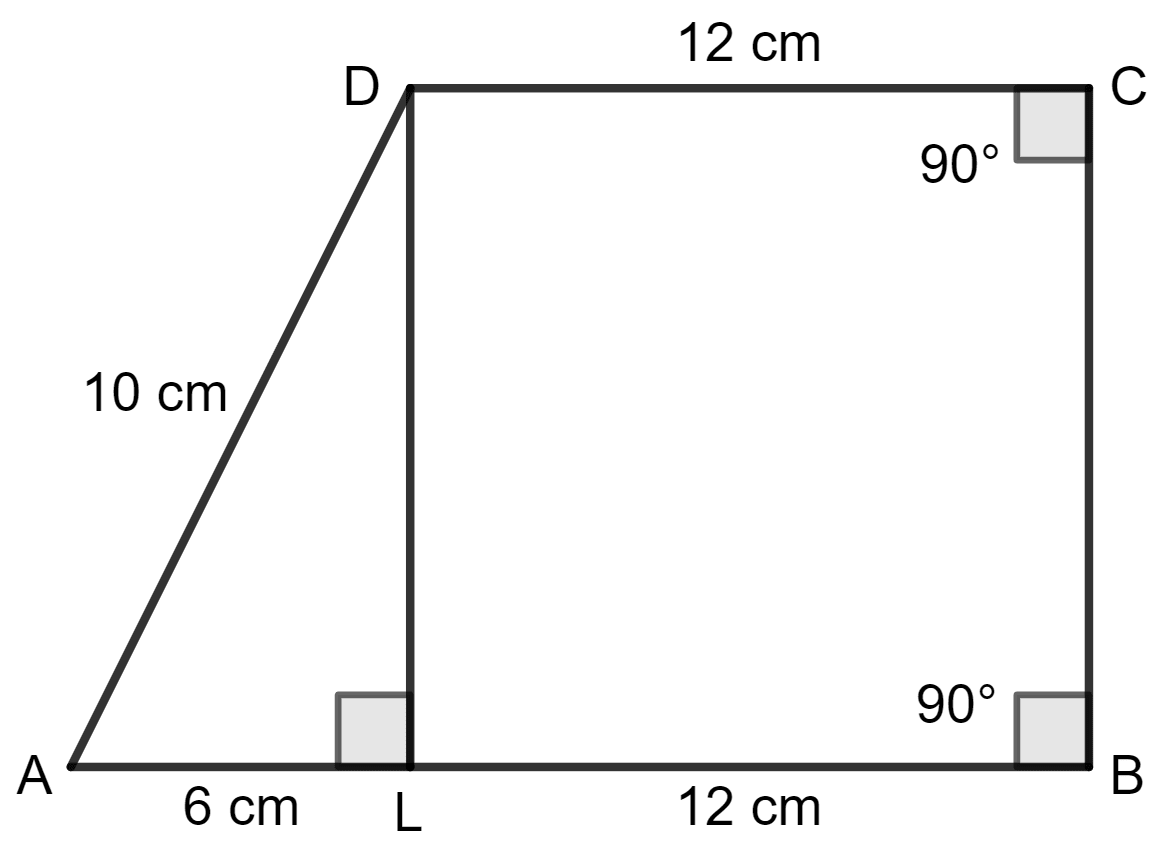
Since, AL = AB - DC
= 18 - 12
= 6 cm
Also, DL = BC (Both are perpendiculars)
Using pythagoras theorem,
AD2 = AL2 + LD2
⇒ 102 = 62 + LD2
⇒ 100 = 36 + LD2
⇒ LD2 = 100 - 36
⇒ LD2 = 64
⇒ LD =
⇒ LD = 8 cm
As we know, the area of a trapezium = (sum of parallel sides) x distance betweem the parallel sides.
= (18 + 12) x 8
= x 30 x 8
= x 240
= 120 cm2
Hence, the area of the trapezium is 120 cm2.
The circumference of a circle is numerically same as its area; then its radius is :
4 unit
2 unit
1 unit
none of these
Answer
Given:
The circumference of a circle = The area of a circle
Let r be the radius of the circle.
As we know, the circumference of the circle = 2πr
And, the area of the circle = πr2
So,
⇒ 2πr = πr2
⇒ 2r = r2
⇒ 2 = r
Hence, the radius of the circle is 2 units.
Hence, option 2 is the correct option.
The perimeter of a square of side 11 cm is equal to circumference of a circle; then the diameter of the circle is :
7 cm
7.5 cm
14 cm
3.5 cm
Answer
Given:
The perimeter of a square = The circumference of a circle
Side of the square = 11 cm
As we know, the perimeter of a square = 4 x side
= 4 x 11 cm
= 44 cm
Let r be the radius of the circle.
And, the circumference of the circle = 2πr
⇒ 2πr = 44
Substitute π = :
So, the diameter of the circle = 2 x radius
= 2 x 7 cm
= 14 cm
Hence, option 1 is the correct option.
The circumference of a circle is equal to the sum of the circumferences of two circles with radii 10 cm and 12 cm. The radius of the circle formed is :
2 cm
44 cm
22 cm
244 cm
Answer
Given:
The circumference of a circle = The sum of the circumferences of two circles with radii 10 cm and 12 cm.
As we know, the circumference of a circle = 2πr
For r = 10 cm:
Circumference of the circle = 2 x x 10
= x 10
=
For r = 12 cm
Circumference of the circle = 2 x x 12
= x 12
=
Let R be the radius of the larger circle.
The circumference of the larger circle =
Hence, option 3 is the correct option.
The diameter of a circular wheel is 56 cm. The distance moved by it in 100 rounds is :
176 cm
17600 cm
1760 cm
352 cm
Answer
Given:
The diameter of a circular wheel = 56 cm
Total number of rounds = 100
Since diameter = 2 x Radius
⇒ Radius =
⇒ Radius =
= 28 cm
As we know, the circumference of a circle = 2πr
Total distance = circumference of the circle x number of rounds
= 176 x 100
= 17600 cm
Hence, option 2 is the correct option.
A circular wheel of radius 3.5 cm makes 600 rounds in 48 seconds, its speed is :
275 cm/s
27.5 m/s
550 cm/s
55 cm/s
Answer
Given:
Radius of circular wheel = 3.5 cm
Total rounds = 600
Total time = 48 seconds
As we know, the circumference of a circle = 2πr
Total distance = The circumference of the circle x number of rounds
= 22 x 600
= 13200 cm
And, Speed =
=
= 275 cm/s
Hence, option 1 is the correct option.
Find the radius and area of a circle, whose circumference is :
(i) 132 cm
(ii) 22 m
Answer
(i) Let r be the radius of the circle.
The circumference of a circle = 132 cm
As we know, the circumference of the circle = 2πr
And, area of the circle = πr2
Hence, the radius of the circle is 21 cm and the area is 1,386 cm2.
(ii) Let r be the radius of the circle.
The circumference of a circle = 22 cm
As we know, the circumference of the circle = 2πr
And, area of the circle = πr2
Hence, the radius of the circle is 3.5 m and the area is 38.5 m2.
Find the radius and circumference of a circle, whose area is :
(i) 154 cm2
(ii) 6.16 m2
Answer
(i) Let r be the radius of the circle.
The area of circle = 154 cm2
As we know, the area of the circle = πr2
Circumference of the circle = 2πr
Hence, the radius of the circle is 7 cm and the circumference is 44 cm.
(ii) Let r be the radius of the circle.
The area of circle = 6.16 m2
As we know, the area of the circle = πr2
Circumference of the circle = 2πr
Hence, the radius of the circle is 1.4 m and the circumference is 8.8 m.
The circumference of a circular table is 88 m. Find its area.
Answer
Given:
The circumference of a circular table = 88 m
Let r be the radius of the circle.
As we know, the circumference of the circle = 2πr
The area of the circle = πr2
Hence, the area of the circular table is 616 m2.
The area of a circle is 1386 sq. cm, find its circumference.
Answer
Given:
The area of a circle = 1386 sq. cm
Let r be the radius of the circle.
As we know, the area of the circle = πr2
Circumference of the circle = 2πr
Hence, the circumference of the circle is 132 cm.
Find the area of a flat circular ring formed by two concentric circles (circles with same centre) whose radii are 9 cm and 5 cm.
Answer
Given:
Radius of outer circle = 9 cm
Radius of inner circle = 5 cm
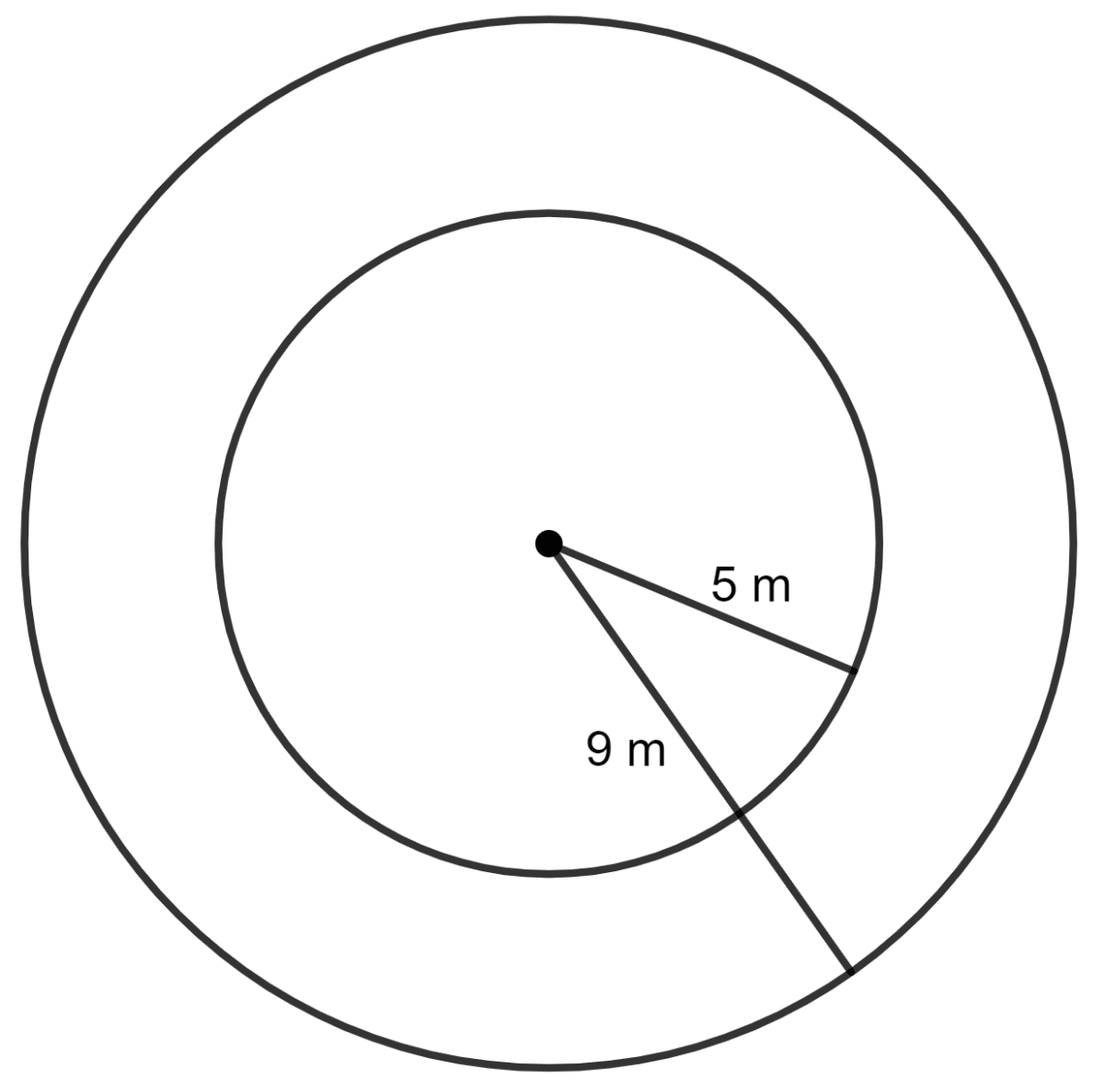
Area of circular ring = Area of outer circle - Area of inner circle
As we know, the area of the circle = πr2
Area of circular ring =
Hence, the area of the circular ring is 176 cm2.
The radii of the inner and outer circumferences of a circular-running-track are 63 m and 70 m respectively. Find :
(i) the area of the track
(ii) the difference between the lengths of the two circumferences of the track
Answer
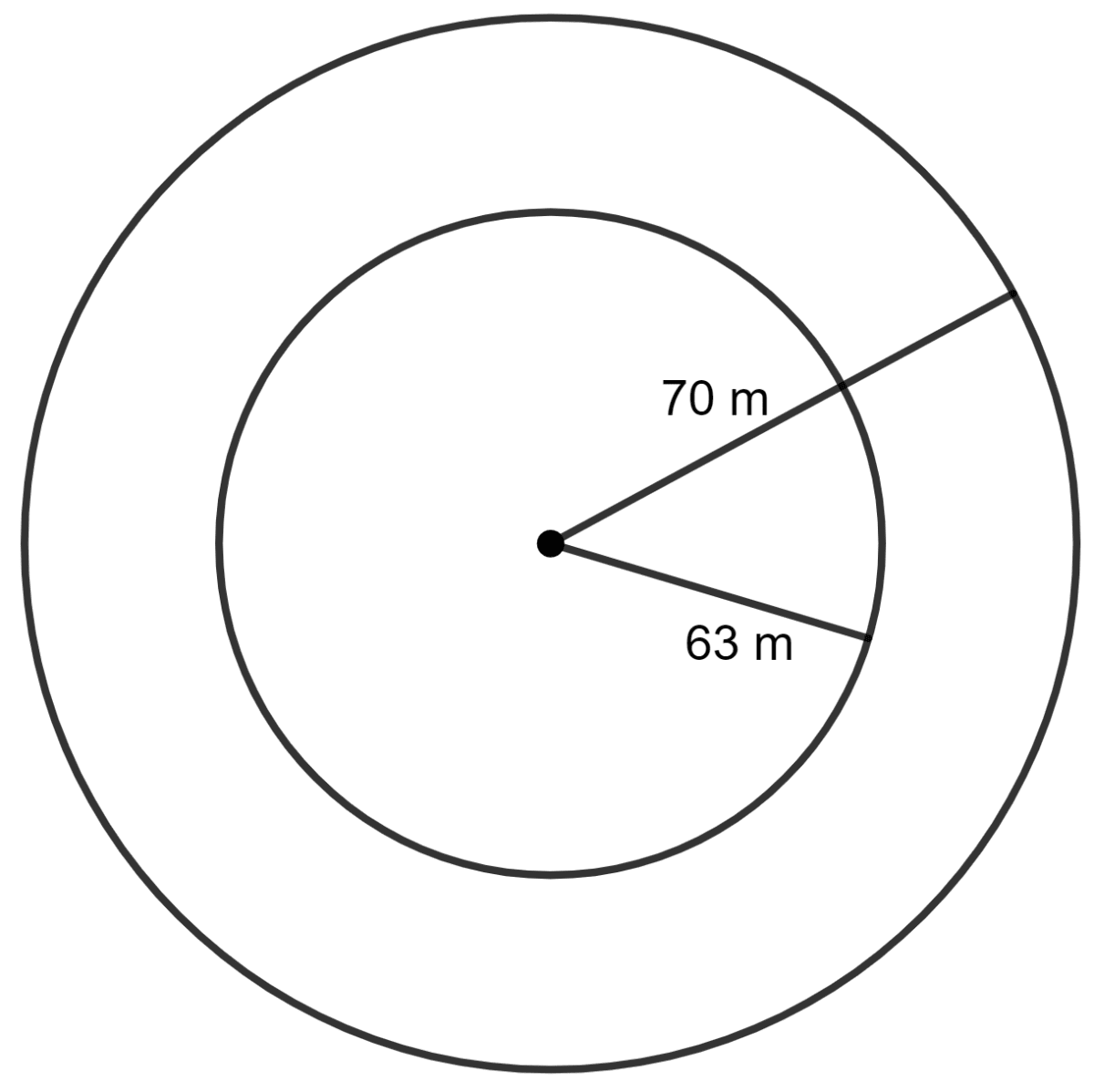
(i) Given:
Radius of outer circle = 70 m
Radius of inner circle = 63 m
Area of circular track = Area of outer circle - Area of inner circle
As we know, the area of the circle = πr2
Area of circular ring =
Hence, the area of the circular track is 2,926 m2.
(ii) The difference between the lengths of the two circumferences of the track = Circumference of outer circle - Circumference of inner circle
As we know, the circumference of the circle = 2πr
The difference between the lengths of the two circumferences of the track =
Hence, the difference between the lengths of the two circumferences of the track is 44 m.
A circular field of radius 105 m has a circular path of uniform width of 5 m along and inside its boundary. Find the area of the path.
Answer
Given:
Radius of outer circular field = 105 m
Radius of inner circular field = 105 - 5 m
= 100 m
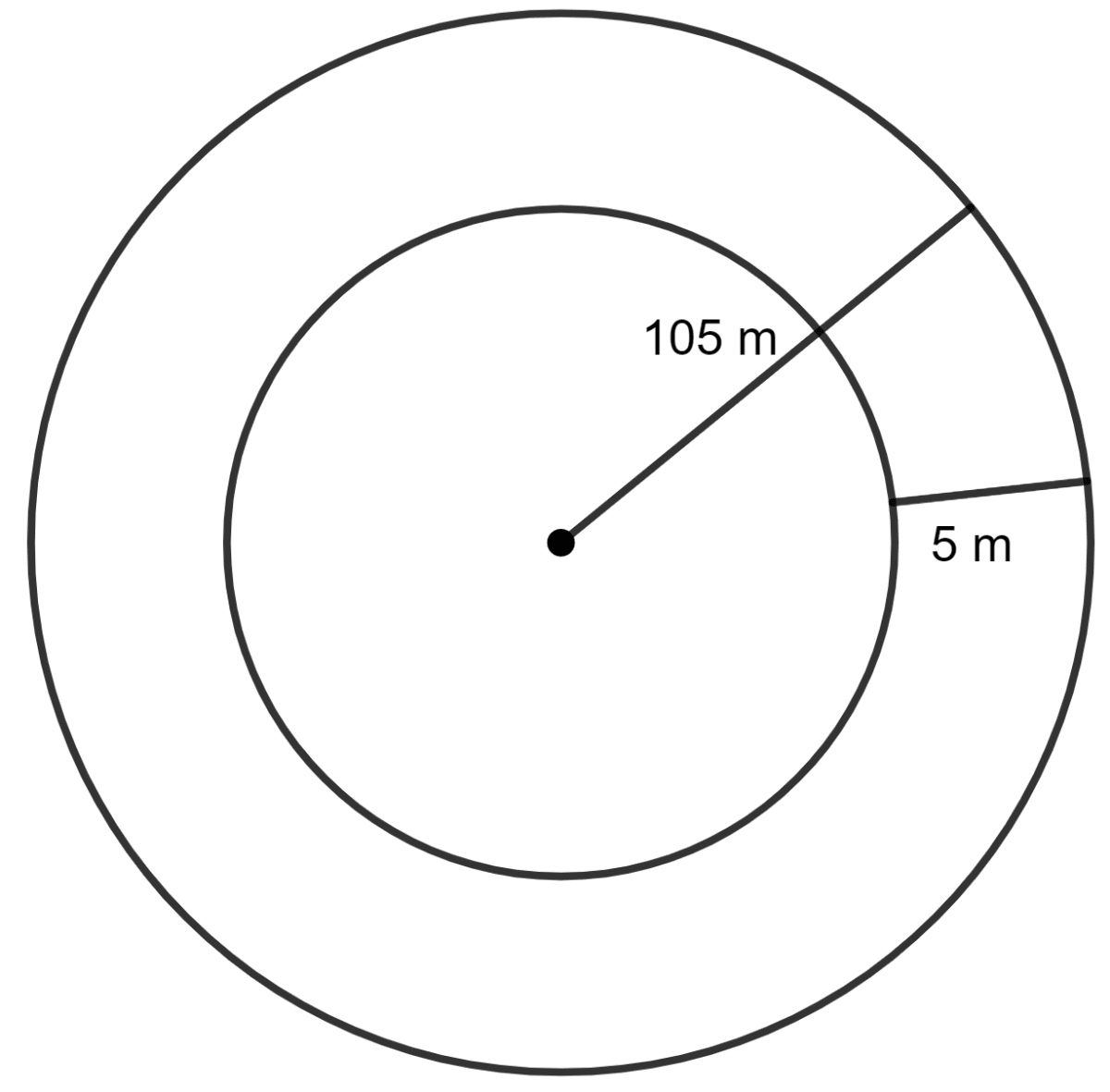
Area of circular ring = Area of outer circular field - Area of inner circular field
As we know, the area of the circle = πr2
Area of circular ring =
Hence, the area of circular field is m2.
A wire, when bent in the form of a square, encloses an area of 484 cm2. Find :
(i) one side of the square
(ii) length of the wire
(iii) the largest area enclosed, if the same wire is bent to form a circle.
Answer
Given:
Area of the square = 484 cm2
Let s be the side of the square.
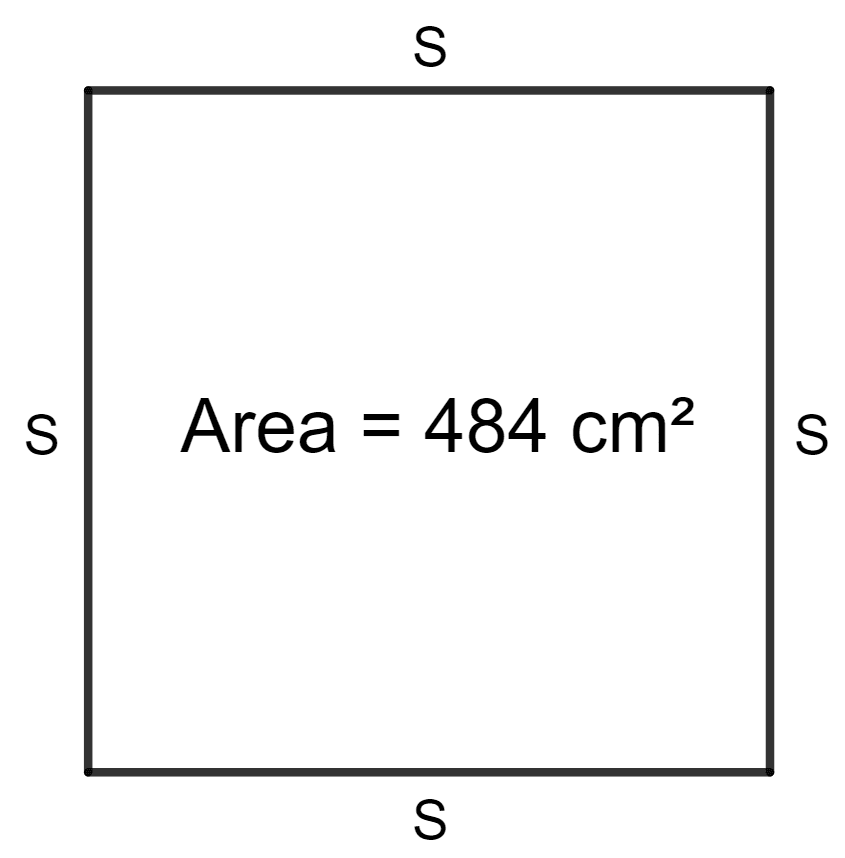
As we know, the area of the square = side2
⇒ s2 = 484
⇒ s =
⇒ s = 22
Hence, one side of square is 22 cm.
(ii) Total length of the wire = perimeter of the square
As we know, the perimeter of the square = 4 x side
= 4 x 22
= 88 cm
Hence, the length of the wire is 88 cm.
(iii) Perimeter of the square = circumference of the circle
Let r be the radius of the circle.
⇒ 2πr = 88 cm
Area of the circle = πr2
Hence, the largest area that can be enclosed when the same wire is bent to form a circle is 616 cm2.
A wire, when bent in the form of a square, encloses an area of 196 cm2. If the same wire is bent to form a circle, find the area of the circle.
Answer
Given:
Area of the square = 196 cm2
Let s be the side of the square.
As we know, the area of the square = side2
⇒ s2 = 196
⇒ s =
⇒ s = 14
As we know, the perimeter of the square = 4 x side
= 4 x 14
= 56 cm
Perimeter of the square = circumference of the circle
Let r be the radius of the circle.
⇒ 2πr = 56
Area of the circle = πr2
Hence, the area of the circle is 249.45 cm2.
The radius of a circular wheel is 42 cm. Find the distance traveled by it in :
(i) 1 revolution
(ii) 50 revolutions
(iii) 200 revolutions
Answer
(i) Given:
The radius of a circular wheel = 42 cm = 0.42 m
As we know, the circumference of the circle = 2πr
Hence, the distance traveled by wheel in 1 revolution is 2.64 m.
(ii) Distance traveled by wheel in 50 revolutions = Circumference of the wheel x 50
= 2.64 x 50 m
= 132 m
Hence, the distance traveled by wheel in 50 revolutions is 132 m.
(ii) Distance traveled by wheel in 200 revolutions = Circumference of the wheel x 200
= 2.64 x 200 m
= 528 m
Hence, the distance traveled by wheel in 200 revolutions is 528 m.
The diameter of wheel is 0.70 m. Find the distance covered by it in 500 revolutions.
If the wheel takes 5 minutes to make 500 revolutions; find its speed in :
(i) m/s
(ii) km/hr
Answer
(i)Given:
Diameter of wheel = 0.70 m
Radius =
= m
= 0.35 m
As we know, the circumference of the circle = 2πr
Distance traveled by wheel in 500 revolutions = Circumference of the wheel x 500
= 2.2 x 500 m
= 1100 m
Speed =
Time taken by wheel = 5 min = 5 x 60 sec = 300 sec.
Hence, the speed = m/s.
(ii) Speed = m/s
Hence, the speed = 13.2 km/hr.
A bicycle wheel, diameter 56 cm, is making 45 revolutions in every 10 seconds. At what speed, in kilo metre per hour, is the bicycle traveling ?
Answer
Given:
Diameter of wheel = 56 cm
Diameter of wheel in Kilometre = 0.00056 km
Radius =
=
= 0.00028 km
As we know, the circumference of the circle = 2πr
Distance traveled by wheel in 45 revolutions = Circumference of the wheel x 45
= 0.00176 x 45 km
= 0.0792 km
And, speed =
It is given that time taken by wheel = 10 sec = .
Hence, the speed = 28.512 km/hr.
A roller has a diameter of 1.4 m. Find :
(i) its circumference
(ii) the number of revolutions it makes while traveling 61.6 m.
Answer
(i) Given:
Diameter of roller = 1.4 m
Radius =
= m
= 0.7 m
As we know, the circumference of the circle = 2πr
Hence, the circumference of the roller is 4.4 m.
(ii) Let the roller make a revolutions while traveling 61.6 m.
Distance travelled by roller in a revolutions = Circumference of the wheel x a
⇒ 61.6 = 4.4 x a
⇒ a =
⇒ a = 14
Hence, the roller makes 14 revolutions while traveling 61.6 m.
Find the area of the circle, length of whose circumference is equal to the sum of the lengths of the circumferences with radii 15 cm and 13 cm.
Answer
Given:
Length of circumference = Sum of the lengths of the circumferences with radii 15 cm and 13 cm
Let r be the radius of the circle.
As we know, the circumference of the circle = 2πr
So,
⇒ 2πr = 2π x 15 + 2π x 13
So, radius of the circle = 28 cm
And, area of the circle = πr2
Hence, the area of the circle is 2,464 cm2.
A piece of wire of length 108 cm is bent to form a semicircular arc bounded by its diameter. Find its radius and area enclosed.
Answer
Given:
Total length of the wire = 108 cm
Let r be the radius of the circle.
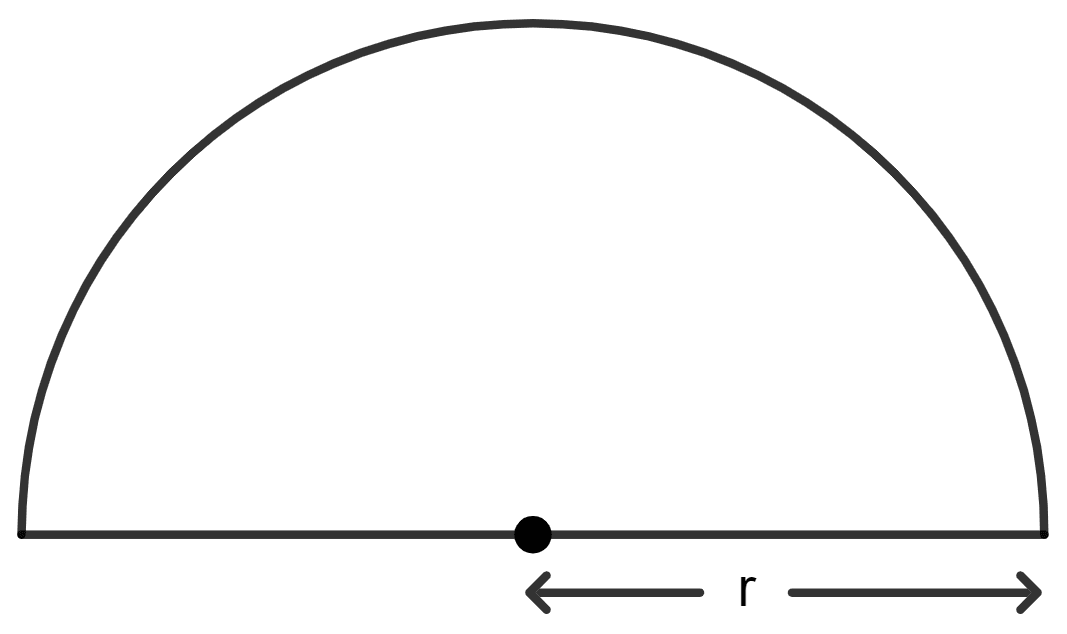
Total length of wire = Circumference of the semicircle + diameter
As we know, the circumference of the semicircle = πr
And, area of the semicircle = πr2
Hence, the radius of the circle is 21 cm and the area is 693 cm2.
In the following figure, a rectangle ABCD encloses three circles. If BC = 14 cm, find the area of the shaded portion.
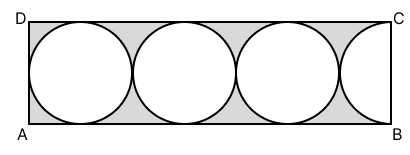
Answer
Given:
BC = 14 cm
AB = 14 + 14 + 14 + 7
= 49 cm
Area of shaded portion = Area of rectangle ABCD - (3 x Area of circle + Area of semicircle)
As we know, the area of rectangle = length x breadth
= 49 x 14 cm2
= 686 cm2
Diameter of the circle = 14 cm
Radius of the circle = cm = 7 cm
Area of the circle = πr2
Area of 3 circles = 3 x 154 cm2 = 462 cm2
Area of the semicircle = πr2
⇒ Area of shaded portion = 686 - (462 + 77) cm2
= 686 - 539 cm2
= 147 cm2
Hence, the area of the shaded portion is 147 cm2.
Each side of a triangle is doubled, the ratio of areas of the original triangle to the new (resulting) triangle is :
1 : 1
4 : 1
1 : 4
1 : 2
Answer
Let a, b and c be sides of the triangle.
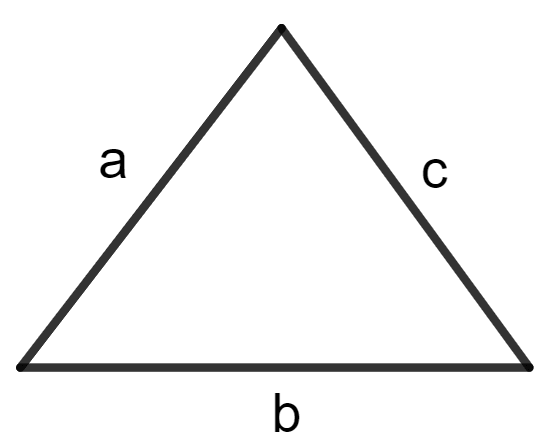
Area of triangle =
When each side of a triangle is doubled, then 2a, 2b and 2c are sides of new triangle.
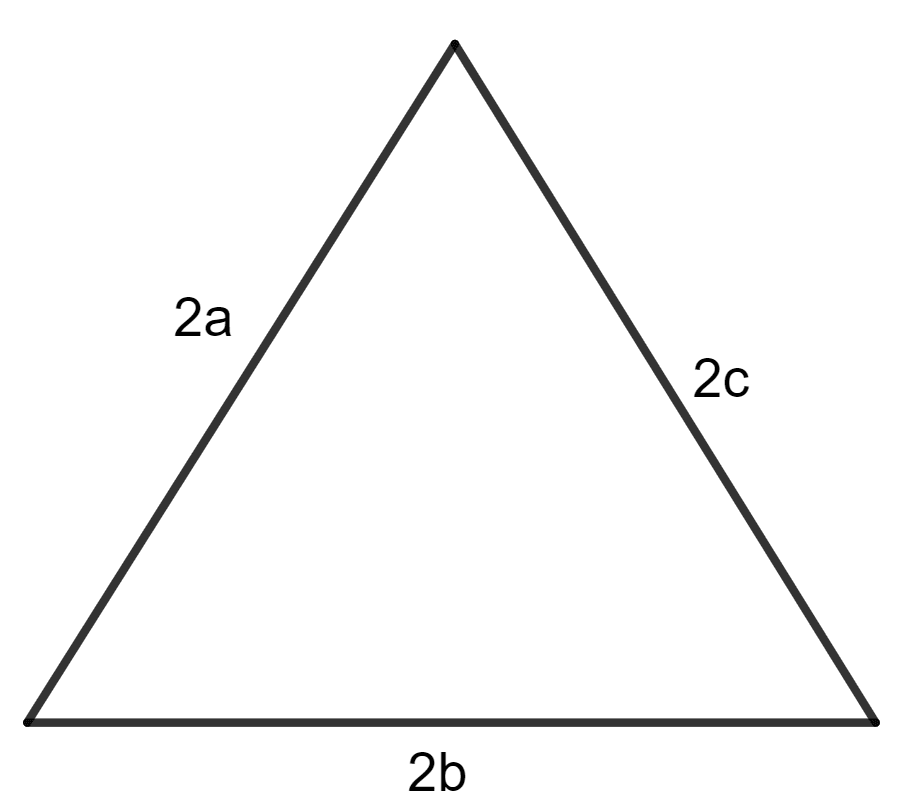
Area of triangle =
=
=
=
= 4
Ratio of original triangle to new triangle =
=
Hence, option 3 is the correct option.
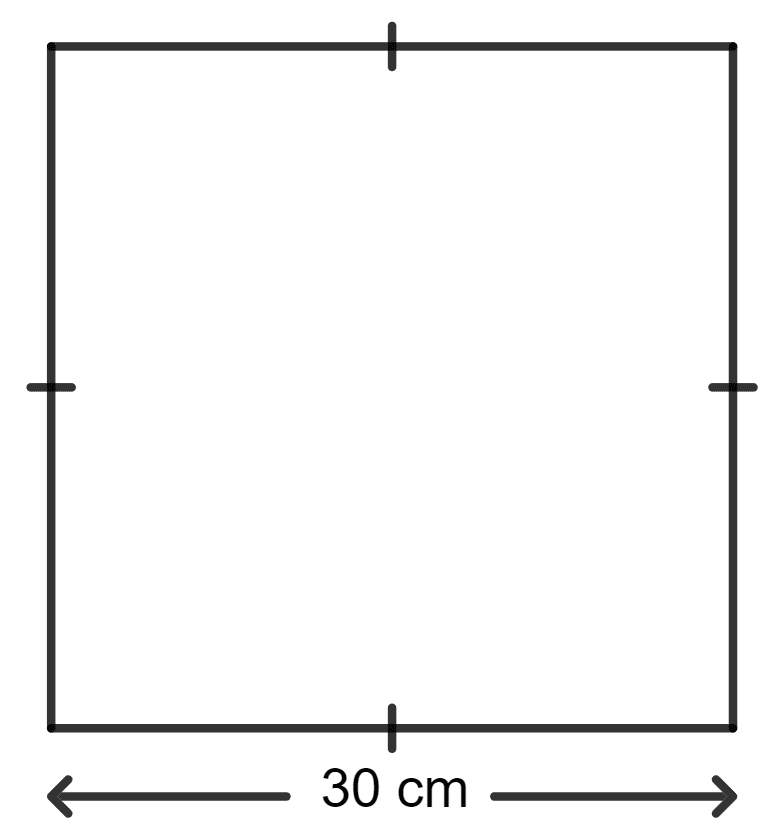
The perimeter of a rectangle is equal to the perimeter of a square. If each side of the square is 30 cm and length of the rectangle is 40 cm; the breadth of the rectangle is :
5 cm
16 cm
15 cm
20 cm
Answer
Given:
The perimeter of a rectangle = The perimeter of a square
Each side of the square = 30 cm
Length of the rectangle = 40 cm
Let b be the breadth of the rectangle.
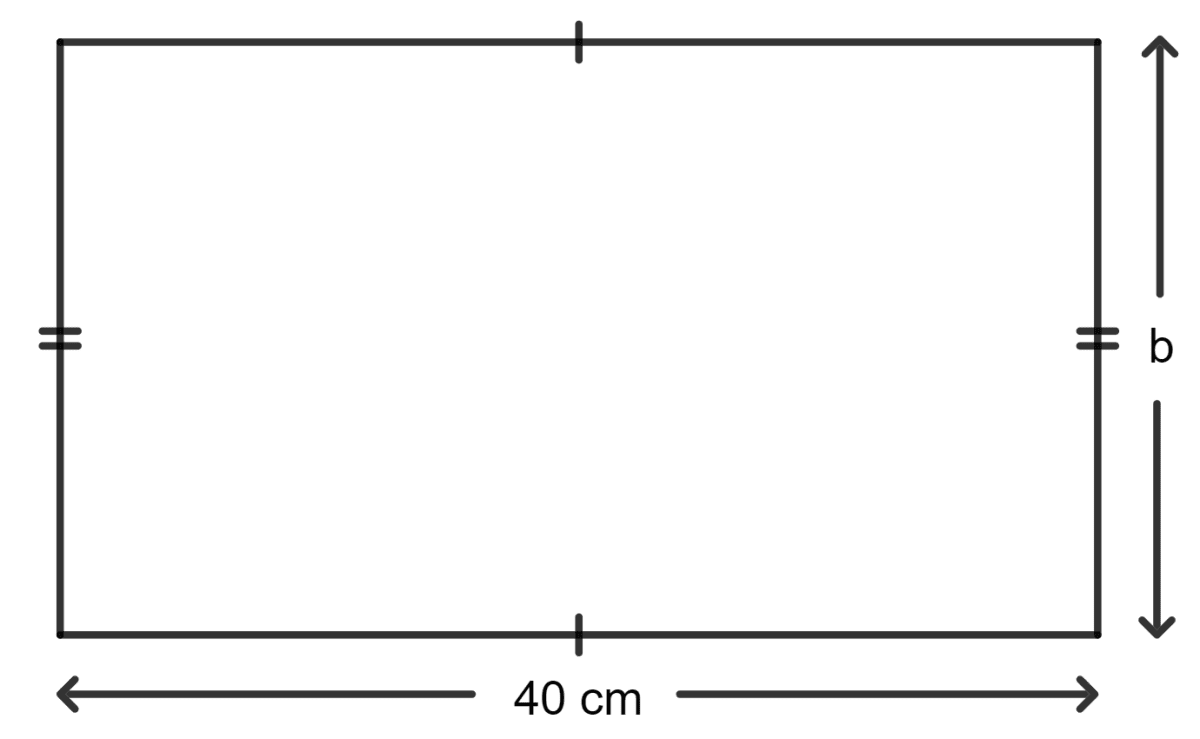
As we know that perimeter of the rectangle = 2(length + breadth)
And, perimeter of the square = 4 x side
⇒ 2(40 + b) = 4 x 30
⇒ 80 + 2b = 120
⇒ 2b = 120 - 80
⇒ 2b = 40
⇒ b =
⇒ b = 20
Hence, option 4 is the correct option.
The area of a trapezium is 80 square unit. If its two parallel sides are 6 unit and 14 unit; the distance between parallel sides is :
4 unit
8 unit
12 unit
1 unit
Answer
Given:
The lengths of the parallel sides of the trapezium are 6 unit and 14 unit.
The area of a trapezium = 80 square unit
Let d be the distance between parallel sides.
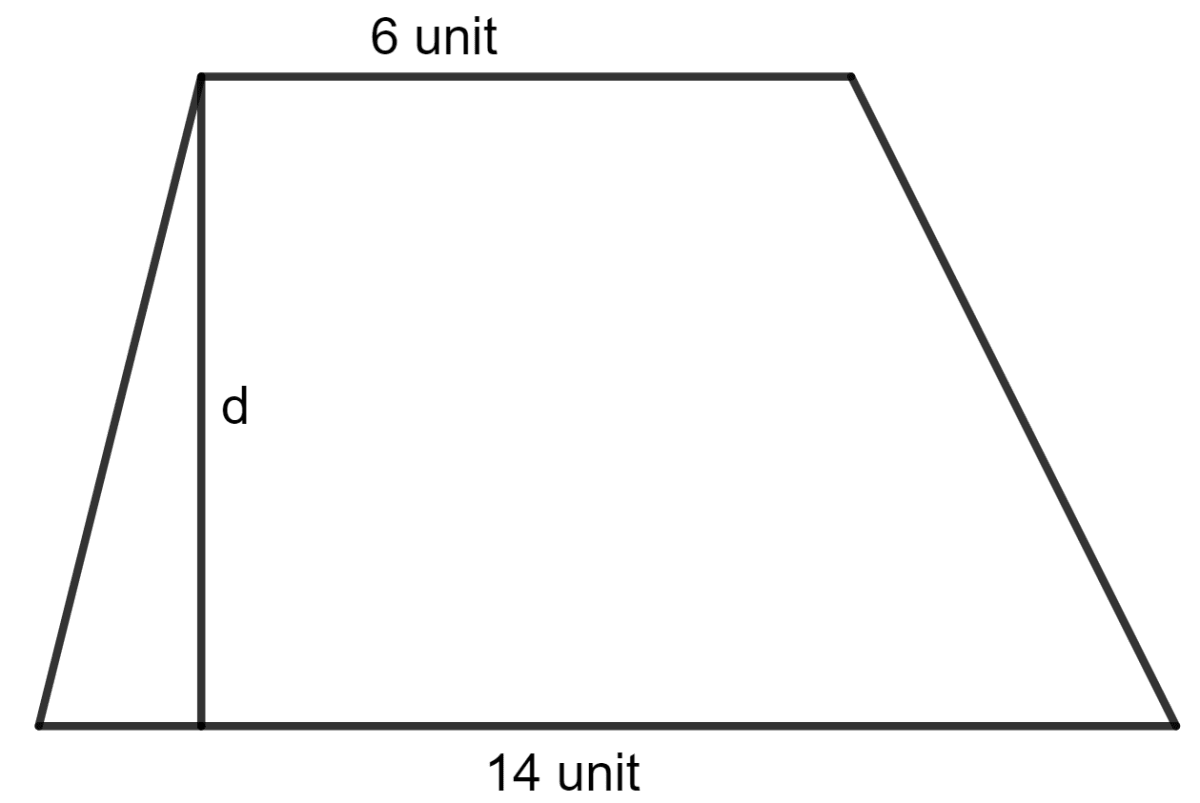
As we know, the area of a trapezium = x (sum of parallel sides) x height
⇒ x (6 + 14) x d = 80
⇒ x 20 x d = 80
⇒ 10 x d = 80
⇒ d =
⇒ d = 8 unit
Hence, option 2 is the correct option.
The external and internal radii of a ring shaped metal sheet are 10 cm and 8 cm respectively. The area of its one face, in terms of π is :
36π cm2
64π cm2
100π cm2
168π cm2
Answer
Given:
Radius of outer circle = 10 cm
Radius of inner circle = 8 cm
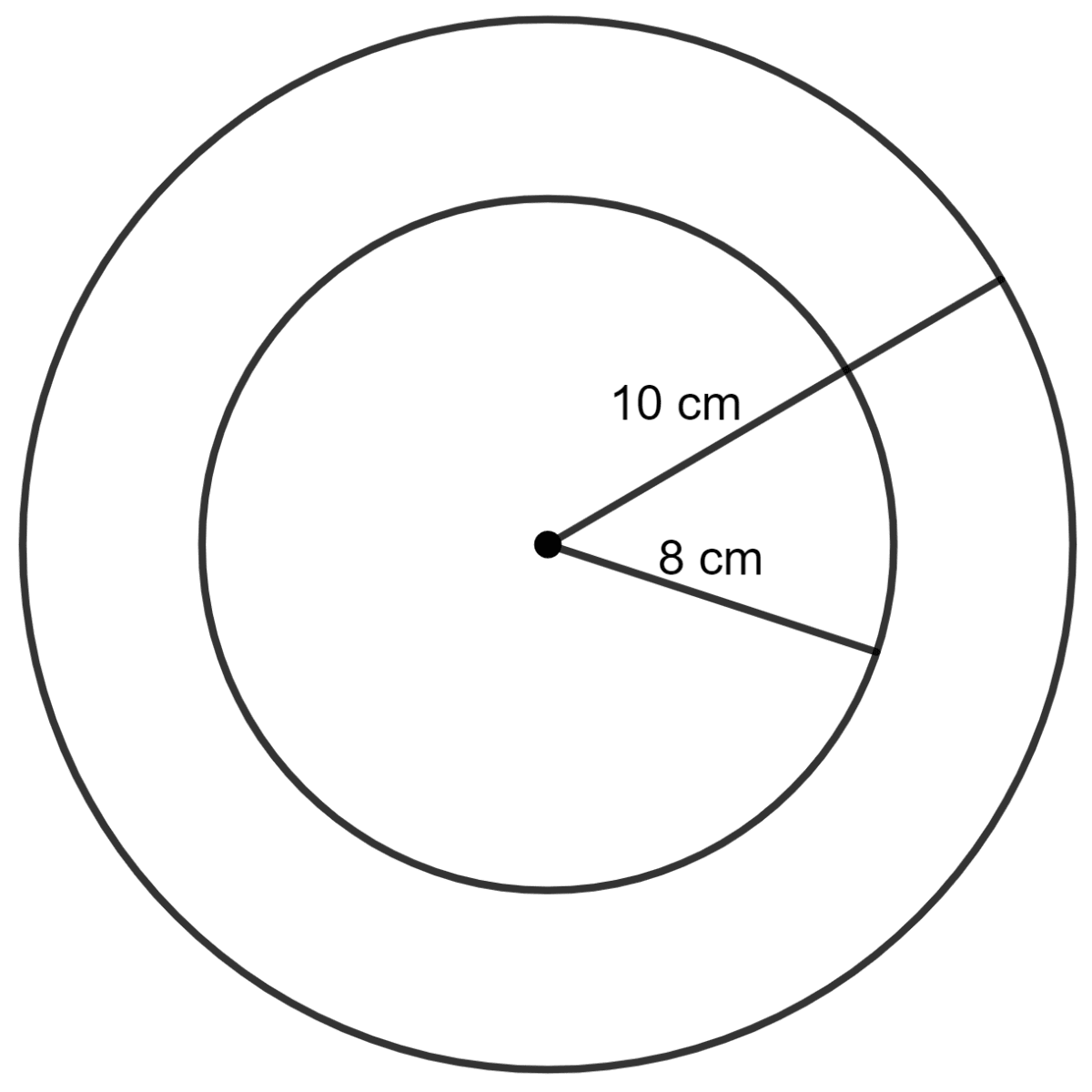
Area of circular ring = Area of outer circle - Area of inner circle
As we know, the area of the circle = πr2
⇒ Area of circular ring = π x (10)2 - π x (8)2
= 100π - 64π
= 36π cm2
Hence, option 1 is the correct option.
The adjacent sides of a rectangle are 20 cm and 24 cm. If its perimeter is equal to the circumference of a circle, the radius of the circle is :
14 cm
21 cm
28 cm
7 cm
Answer
Given:
The adjacent sides of a rectangle are 20 cm and 24 cm.
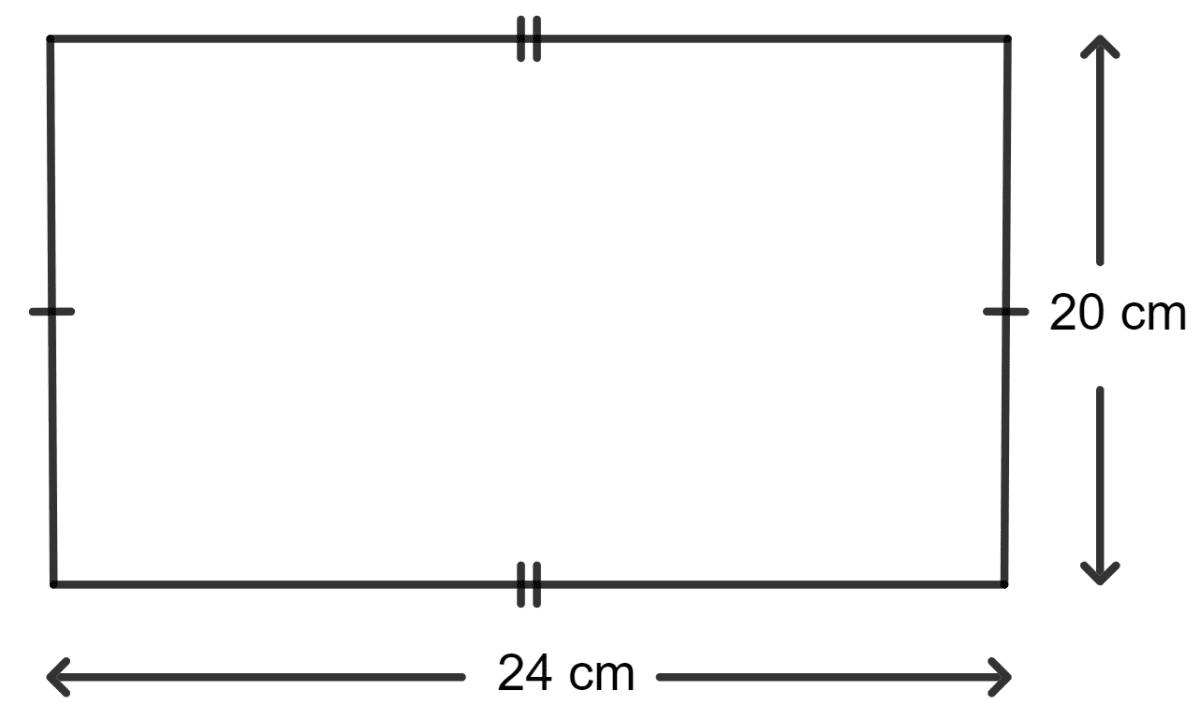
The perimeter of rectangle = The circumference of a circle
Let r be the radius of the circle.
As we know, the perimeter of the rectangle = 2(length + breadth)
And, the circumference of the circle = 2πr
⇒ 2(20 + 24) = 2 x x r
⇒ 2 x 44 = x r
⇒ 88 = x r
⇒ r =
⇒ r =
⇒ r = 14 cm
Hence, option 1 is the correct option.
Statement 1: ABCD is a parallelogram, base AB = 12 cm, perpendicular dropped from D to AB is 9 cm, area of parallelogram ABCD = 54 cm2.
Statement 2: The area of parallelogram = Base x Height.
Which of the following options is correct?
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Answer
Given,
AB (base) = 12 cm, perpendicular dropped from D to AB (height) = 9 cm.
By formula,
The area of parallelogram = Base x Height
= 12 x 9
= 108 cm2.
∴ Statement 1 is false, and statement 2 is true.
Hence, option 4 is the correct option.
Assertion (A) : The diagonal of a rectangle is 17 m and its breadth is 8 m. Half of the area of rectangle is 120 m2.
Reason (R) : The diagonal of every rectangle, divide into two congruent right-triangles.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
Given,
The diagonal of the rectangle = 17 m
The breadth of the rectangle = 8 m
Using Pythagoras theorem in rectangle,
⇒ Diagonal2 = Length2 + Breadth2
⇒ 172 = l2 + 82
⇒ 289 = l2 + 64
⇒ l2 = 289 - 64
⇒ l2 = 225
⇒ l =
⇒ l = 15 m.
By formula,
Area of rectangle = l x b = 15 x 8 = 120 m2.
Half of the area of rectangle = = 60 m2.
So, assertion (A) is false.
ABCD is a rectangle. BD is a diagonal.
In Δ ABD and Δ BDC,
⇒ AB = DC (Opposite sides of rectangle are equal)
⇒ AD = BC (Opposite sides of rectangle are equal)
⇒ BD = BD (Common)
∴ Δ ABD ≅ Δ BDC (By SSS congruency criterion)
Thus the diagonal of every rectangle, divide into two congruent right-triangles.
So, reason (R) is true.
∴ A is false, but R is true.
Hence, option 4 is the correct option.
Assertion (A) : The area of an equilateral triangle of height cm2.
Reason (R) : The area of an equilateral triangle = x (Height)2.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
Given, height of the equilateral triangle = 2 cm
By formula,
The area of an equilateral triangle = x (Height)2
So, reason (R) is true.
Substituting values we get :
So, assertion (A) is true.
∴ Both A and R are correct, and R is the correct explanation for A.
Hence, option 1 is the correct option.
Assertion (A) : The diagonal of a square is cm. Its area = 81 cm2.
Reason (R) : The area of a square = x d2, where d is the length of the diagonal
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
Given, the diagonal of a square = cm
By formula,
The area of a square = x d2, where d is the length of the diagonal.
So, reason (R) is true.
Given,
The diagonal of a square is cm.
So, assertion (A) is true.
∴ Both A and R are correct, and R is the correct explanation for A.
Hence, option 1 is the correct option.
Assertion (A) : The area of trapezium with base 10 cm, height 5 cm and the side parallel to the given base being 6 cm is 40 cm2.
Reason (R) : The area of trapezium = x (sum of non parallel sides) x height.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are incorrect.
A is true, but R is false.
A is false, but R is true.
Answer
Given,
Base = 10 cm
Height = 5 cm
The side parallel to the given base = 6 cm
By formula,
Area of trapezium = x (sum of parallel sides) x height.
∴ A is true, but R is false.
Hence, option 3 is the correct option.
The perimeter of a trapezium is 52 cm. If its non-parallel sides are 10 cm each and its altitude is 8 cm, find the area of the trapezium.
Answer
The perimeter of a trapezium = 52 cm.
The altitude = 8 cm
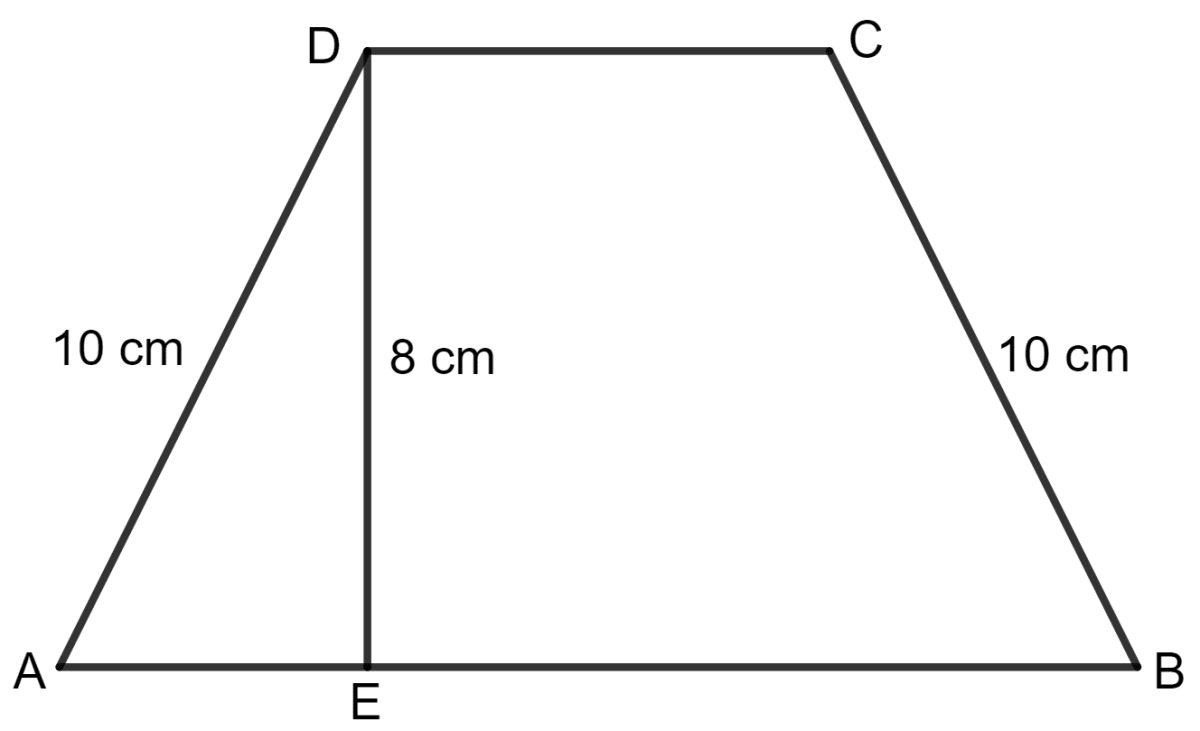
Perimeter of the trapezium = AB + BC + CD + DA
⇒ 52 = AB + 10 + CD + 10
⇒ 52 = AB + CD + 20
⇒ AB + CD = 52 - 20
⇒ AB + CD = 32
⇒ Sum of parallel sides = 32
As we know, the area of a trapezium = x (sum of parallel sides) x height
= x 32 x 8 cm2
= x 256 cm2
= 128 cm2
Hence, the area of the trapezium is 128 cm2.
The shape of a garden is rectangular in the middle and semicircular at each end as shown in the figure. Find the area and perimeter of the garden.
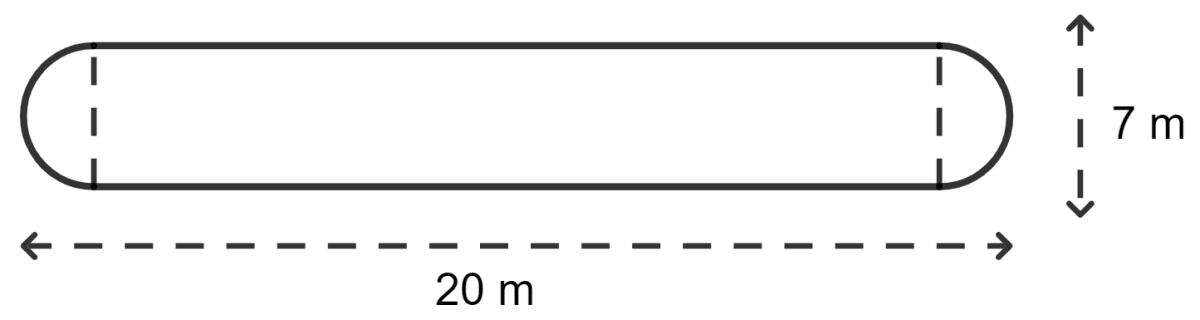
Answer
Given:
Total length of garden = 20 m
Radius of the circle = m
Length of rectangle = total length - 2 x radius of the circle
= 20 - 2 x m
= 20 - 7 m
= 13 m
Perimeter of the figure = l + l + 2 x x circumference of semicircle
As we know that circumference of the circle = 2πr
= 13 + 13 + 2 x x 2πr
= 26 + 2 x
= 26 +
= 26 + 22
= 48 m
Area of the figure = Area of rectangle + 2 x Area of semicircle
As we know that area of rectangle = length x breadth
And, area of the circle = πr2
So, area
Hence, the area of the garden is 129.5 m2 and the perimeter is 48 m.
Each side of rhombus is 13 cm and one of its diagonals is 10 cm. Find :
(i) the length of its other diagonal
(ii) its area.
Answer
(i) Given :
AB = 13 cm
AC = 10 cm
Then, OA = OC = = 5 cm
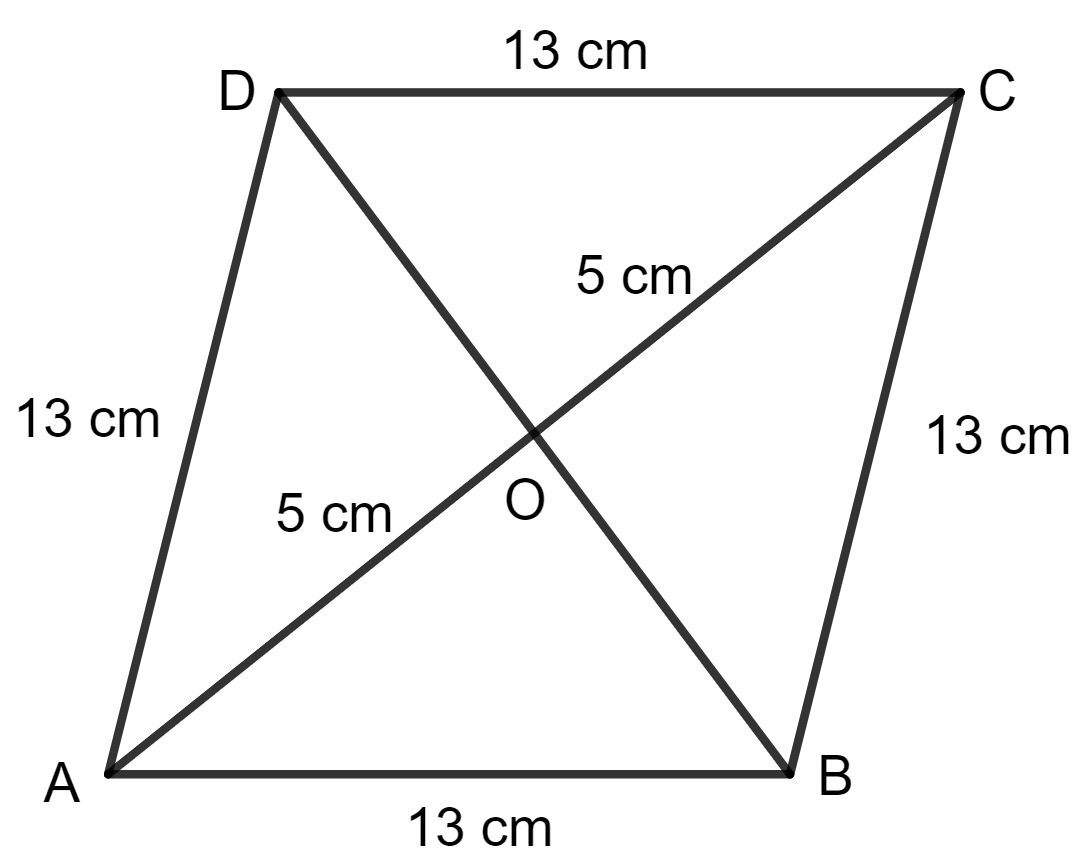
Since the diagonals of a rhombus bisect at 90°.
Applying pythagoras theorem in triangle AOB, we get:
AB2 = OA2 + OB2
⇒ (13)2 = (5)2 + OB2
⇒ 169 = 25 + OB2
⇒ OB2 = 169 - 25
⇒ OB2 = 144
⇒ OB =
⇒ OB = 12
BD = 2 x OB
= 2 x 12 cm
= 24 cm
Hence, the length of other diagonal is 24 cm.
(ii) As we know, the area of rhombus = x product of its diagonal
= x 10 x 24 cm2
= x 240 cm2
= 120 cm2
Hence, the area of the rhombus is 120 cm2.
The given figure shows a rectangle ABCD and a right triangle BOC. Find the area of the shaded portion.
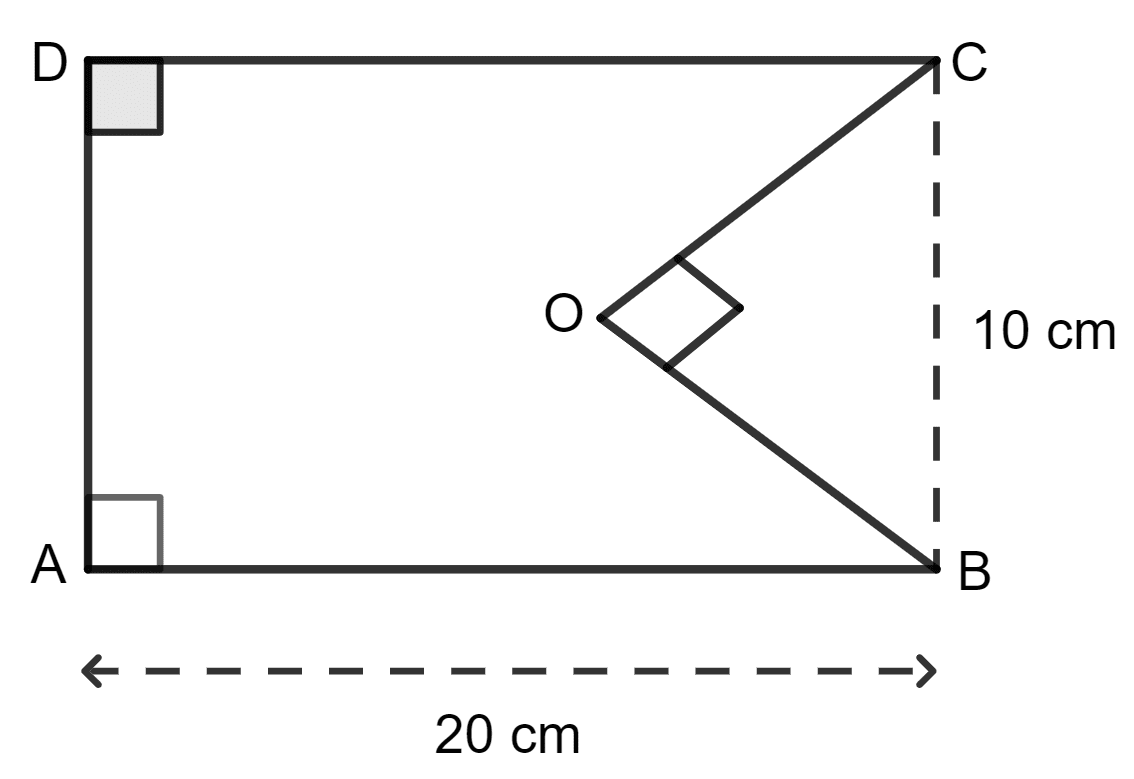
Answer
Given:
Length of rectangle = 20 cm
Breadth of rectangle = 10 cm
Height of triangle = 8 cm
Hypotenuse of triangle = 10 cm
Applying pythagoras theorem in triangle COB, we get:
BC2 = OB2 + OC2
⇒ (10)2 = OB2 + (8)2
⇒ 100 = OB2 + 64
⇒ OB2 = 100 - 64
⇒ OB2 = 36
⇒ OB =
⇒ OB = 6 cm
Area of shaded figure = area of rectangle - area of triangle
As we know that area of rectangle = length x breadth
And, area of the triangle = x base x height
So, Area
Hence, the area of the shaded portion is 176 cm2.
Find the area of the circle whose circumference is 264 cm.
Answer
Let r be the radius of the circle.
The circumference of a circle = 264 cm
As we know, the circumference of the circle = 2πr
And, area of the circle = πr2
Hence, the area of the circle is 5,544 cm2.
Find the circumference of a circle whose area is 1386 cm2.
Answer
Let r be the radius of the circle.
The area of circle = 1386 cm2
As we know, the area of the circle = πr2
Circumference of the circle = 2πr
Hence, the circumference of the circle is 132 cm.
A copper wire when bent in the form of a square encloses an area of 484 cm2. When the same wire is bent in the form of a circle, find the area of the circle formed.
Answer
Given:
Area of the square = 484 cm2
Let s be the side of the square.

As we know, the area of the square = side2
⇒ s2 = 484
⇒ s =
⇒ s = 22 cm
Total length of the wire = Perimeter of the square
As we know, the perimeter of the square = 4 x side
= 4 x 22
= 88 cm
Perimeter of the square = Circumference of the circle
Let r be the radius of the circle.
⇒ 2πr = 88 cm
Area of the circle = πr2
Hence, the area of the circle is 616 cm2.
The perimeters of two squares are 120 cm and 64 cm. Find the perimeter of the square whose area is equal to the sum of the areas of these two squares.
Answer
Given:
The perimeters of two squares are 120 cm and 64 cm.
Let a be the side of the square.
As we know that perimeter of the square = 4 x side
⇒ 4 x a = 120
⇒ a =
⇒ a = 30 cm
The perimeter of square is 64 cm.
Let b be the side of the square.
As we know that perimeter of the square = 4 x side
⇒ 4 x b = 64
⇒ a =
⇒ a = 16 cm
It is given that area of third square = the sum of the areas of these two squares
Let R be the side of the square.
As we know that area of the square = side2
⇒ R2 = 302 + 162
⇒ R2 = 900 + 256
⇒ R2 = 1156
⇒ R =
⇒ R = 34 cm
Perimeter of third square = 4 x 34 cm
= 136 cm
Hence, the perimeter of the square is 136 cm.
Find the perimeter of a square whose area is equal to half the sum of areas of three squares with sides 3 cm, 4 cm and 5 cm.
Answer
Given:
Area of square = Half the sum of areas of three squares with sides 3 cm, 4 cm and 5 cm.
Let R be the side of the square.
As we know that area of the square = side2
And, perimeter of the square = 4 x side
Perimeter of the square = 4 x 5 cm
= 20 cm
Hence, the perimeter of the square is 20 cm.
If the diameter of a car wheel is 28 cm, how many times will the wheel rotate in a journey of 11 km ?
Answer
Given:
Diameter of wheel = 28 cm
Radius =
= cm
= 14 cm
As we know, the circumference of the circle = 2πr
Let a be the number of revolutions.
Total distance = 11 km
= 11 x 1,00,000 cm
= 11,00,000 cm
Distance traveled by wheel in a revolutions = circumference of the wheel x a
⇒ 11,00,000 = 88 x a
⇒ a =
⇒ a = 12,500 revolutions
Hence, the wheel rotates 12,500 times during a journey of 11 km.