Lower class limit of 15-18 is :
15
18
Answer
The lower class limit is defined as the smaller number in the interval.
Thus, the lower class limit of 15-18 is 15.
Hence, option 1 is the correct option.
Upper class limit of 5-12.5 is :
5
12.5
Answer
The upper class limit is defined as the larger number in the interval.
Thus, the upper class limit of 5-12.5 is 12.5.
Hence, option 2 is the correct option.
If the upper and the lower limits of a class interval are 16 and 10, the class-mark is :
6
3
13
none of these
Answer
Hence, option 3 is the correct option.
If the lower and the upper limits of a class interval are 7.5 and 12.5, the class-mark is :
10
2.5
7.5
12.5
Answer
Hence, option 1 is the correct option.
In a pie-chart, an angle of 30° represents 80 articles. The number of articles represented by 105° are :
280
200
none of these
Answer
It is given that an angle of 30° represents 80 articles.
Therefore, the number of articles represented by an angle of 1° is:
= articles = articles
The number of articles represented by an angle of 105° is:
= articles.
=
= 280 articles
Hence, option 1 is the correct option.
In a pie-chart, 76 articles are represented by 19°; how many articles will be represented by 76° ?
19
76
304
none of these
Answer
It is given that an angle of 19° represents 76 articles.
Therefore, an angle of 1° represents:
= 4 articles
The number of articles represented by an angle of 76° = 76 x 4 = 304 articles
Hence, option 3 is the correct option.
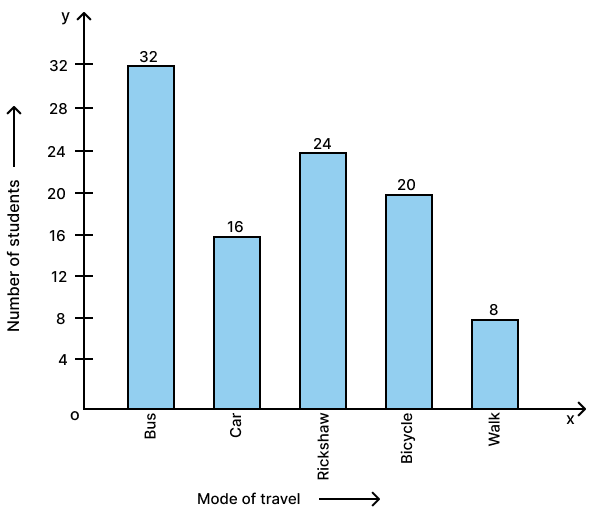
Hundred students from a certain locality use different modes of traveling to school as given below. Draw a bar graph.
| Bus | Car | Rickshaw | Bicycle | Walk |
|---|---|---|---|---|
| 32 | 16 | 24 | 20 | 8 |
Answer
Steps:
On a graph paper, draw two mutually perpendicular lines OX and OY which intersect each other at point O.
The line OX is taken horizontal and is called the x-axis, whereas the line OY is taken vertical and is called the y-axis.
On the x-axis, starting from O, mark points at equal distances. At these points write the names of different modes of travel given. In this question, the names are Bus, Car, Rickshaw, Bicycle and Walk.
Along y-axis, mark the heights of the bars (rectangles) in proportion to the given data (number of students).
Remember:
(i) The heights of different bars (rectangles) are parallel to y-axis and the mid-points of their bases are on the points marked on the x-axis (step 2).
(ii) The bars may be taken of any suitable width, but widths of all the bars must be the same.
(iii) The space (distance) between consecutive bars may be of any suitable value, but the spaces between all the consecutive bars must be the same.
The required bar graph is as given below:
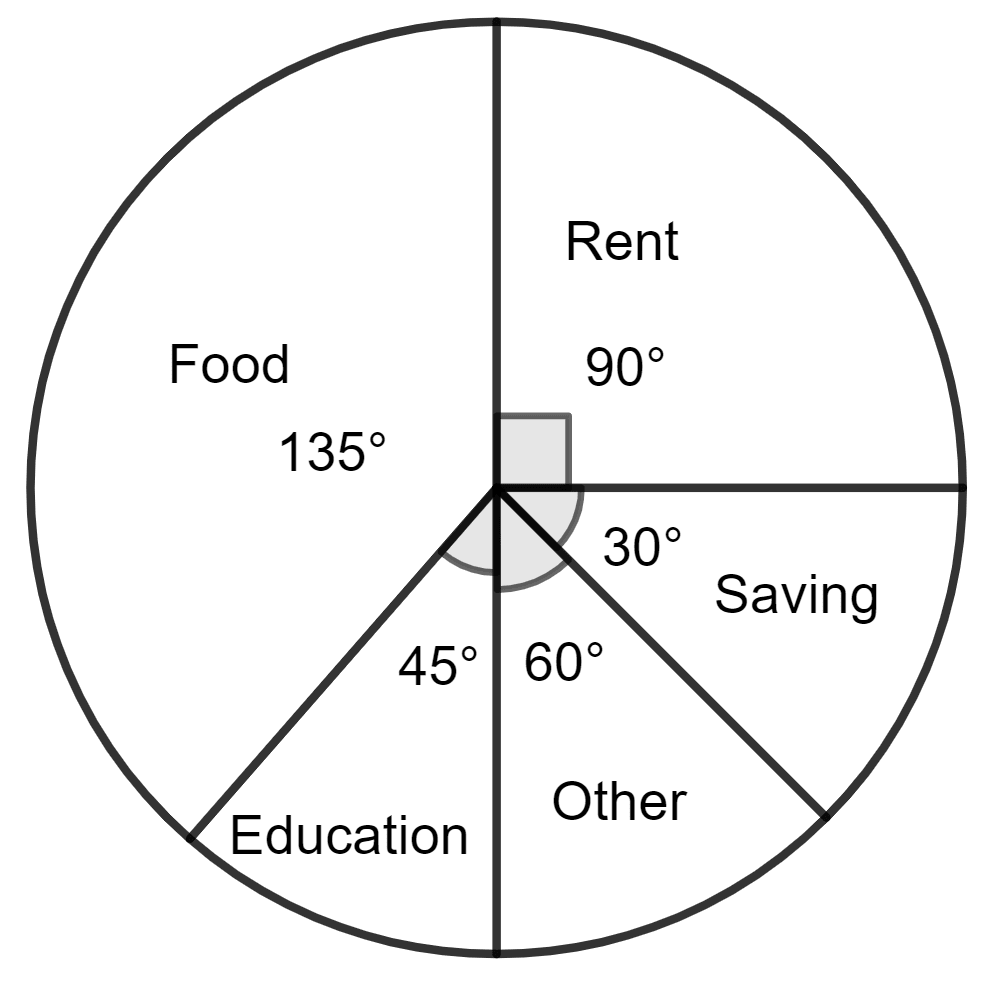
Mr. Mirza's monthly income is ₹ 7,200. He spends ₹ 1,800 on rent, ₹ 2,700 on food, ₹ 900 on education of his children, ₹ 1,200 on other things and saves the rest.
Draw a pie-chart to represent it.
Answer
Steps:
Since the angle about the center of a circle is 360°, divide 360° in proportion to the given data. In this question, divide 360° in proportion 1,800 : 2,700 : 900 : 1,200 to obtain the corresponding central angles.
Make a table as given.
| Monthly spends | Rupees (Rs.) | Central Angles |
|---|---|---|
| Rent | 1,800 | = 90° |
| Food | 2,700 | = 135° |
| Education | 900 | = 45° |
| Other | 1,200 | = 60° |
| Savings | 600 | = 30° |
| Total | 7,200 | 360° |
Draw a circle of any suitable radius.
For each central-angle, draw a sector.
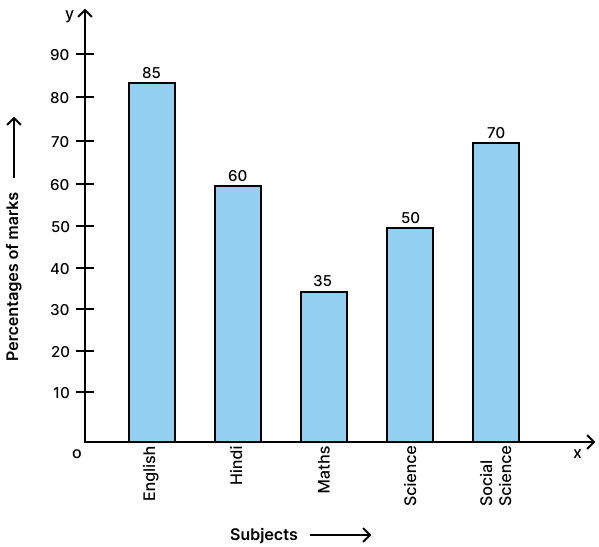
The percentage of marks obtained in different subjects by Ashok Sharma (in an examination) are given below. Draw a bar graph to represent it.
| English | Hindi | Maths | Science | Social Studies |
|---|---|---|---|---|
| 85 | 60 | 35 | 50 | 70 |
Answer
Steps:
On a graph paper, draw two mutually perpendicular lines OX and OY which intersect each other at point O.
The line OX is taken horizontal and is called the x-axis, whereas the line OY is taken vertical and is called the y-axis.
On the x-axis, starting from O, mark points at equal distances. At these points write the names of the different subjects given. In this question, the names are English, Hindi, Maths, Science and Social Studies.
Along y-axis, mark the heights of the bars (rectangles) in proportion to the given data (percentages of marks).
Remember:
(i) The heights of different bars (rectangles) are parallel to y-axis and the mid-points of their bases are on the points marked on the x-axis (step 2).
(ii) The bars may be taken of any suitable width, but widths of all the bars must be the same.
(iii) The space (distance) between consecutive bars may be of any suitable value, but the spaces between all the consecutive bars must be the same.
The required bar graph is as given below:
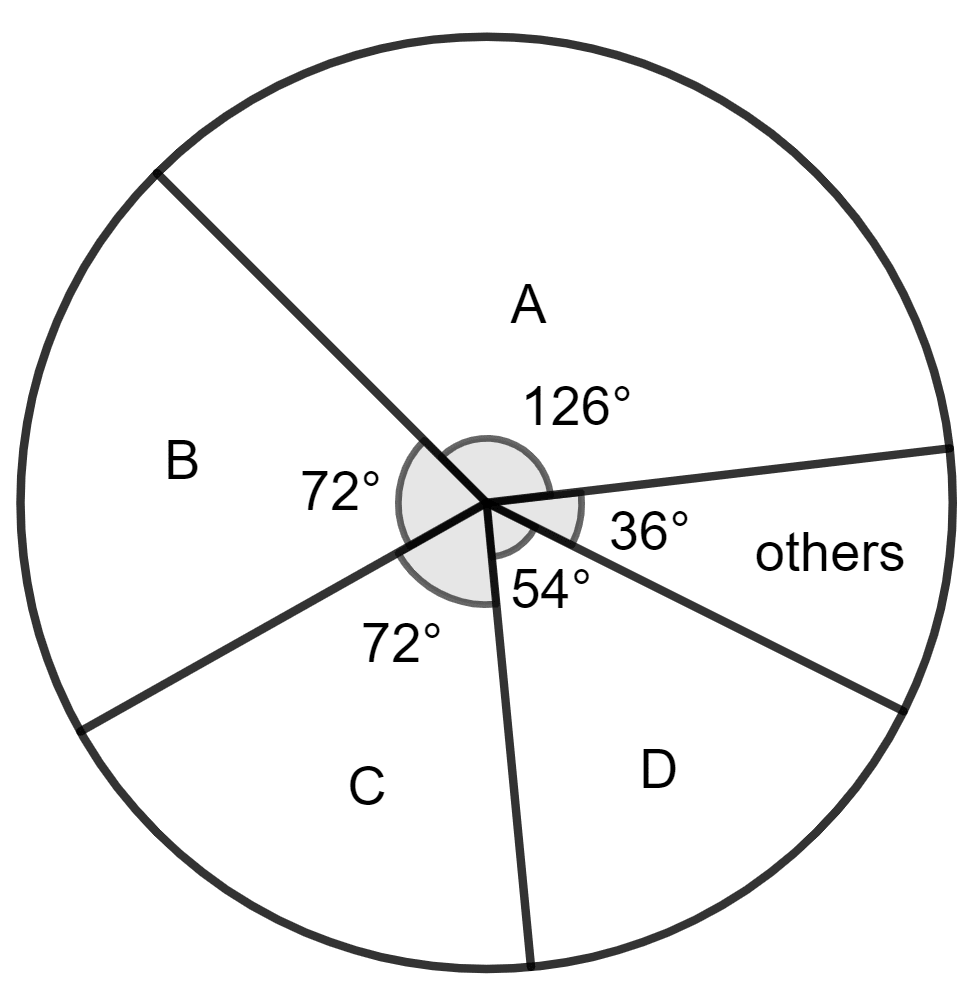
The following table shows the market position of different brands of tea leaves.
| Brands | A | B | C | D | others |
|---|---|---|---|---|---|
| % Buyers | 35 | 20 | 20 | 15 | 10 |
Draw a pie-chart to represent the above information.
Answer
Steps:
Since the angle about the center of a circle is 360°, divide 360° in proportion to the given data. In this question, divide 360° in proportion 35 : 20 : 20 : 15 : 10 to obtain the corresponding central angles.
Make a table as given.
| Brands | Buyers | Central Angles |
|---|---|---|
| A | 35 | = 126° |
| B | 20 | = 72° |
| C | 20 | = 72° |
| D | 15 | = 54° |
| Others | 10 | = 36° |
| Total | 100 | 360° |
Draw a circle of any suitable radius.
For each central-angle, draw a sector.
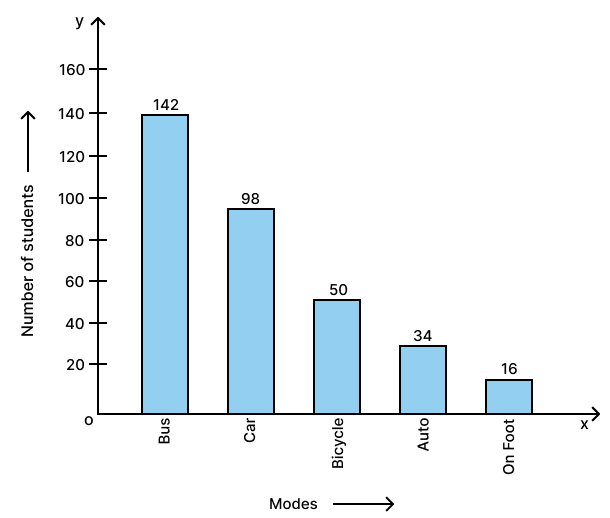
Students of a small school use different modes of travel to school as shown below :
| Modes | Bus | Car | Bicycle | Auto | On foot |
|---|---|---|---|---|---|
| No. of students | 142 | 98 | 50 | 34 | 16 |
Draw a suitable bar graph.
Answer
Steps:
On a graph paper, draw two mutually perpendicular lines OX and OY which intersect each other at point O.
The line OX is taken horizontal and is called the x-axis, whereas the line OY is taken vertical and is called the y-axis.
On the x-axis, starting from O, mark points at equal distances. At these points write the names of the different modes of travel given. In this question, the names are Bus, Car, Bicycle, Auto and On foot.
Along y-axis, mark the heights of the bars (rectangles) in proportion to the given data (Number of students).
Remember:
(i) The heights of different bars (rectangles) are parallel to y-axis and the mid-points of their bases are on the points marked on the x-axis (step 2).
(ii) The bars may be taken of any suitable width, but widths of all the bars must be the same.
(iii) The space (distance) between consecutive bars may be of any suitable value, but the spaces between all the consecutive bars must be the same.
The required bar graph is as given below:
For the following table, draw a bar-graph.
| A | B | C | D | E | F |
|---|---|---|---|---|---|
| 230 | 400 | 350 | 200 | 380 | 160 |
Answer
Steps:
On a graph paper, draw two mutually perpendicular lines OX and OY which intersect each other at point O.
The line OX is taken horizontal and is called the x-axis, whereas the line OY is taken vertical and is called the y-axis.
On the x-axis, starting from O, mark points at equal distances. At these points write the names of the alphabet given. In this question, the names are A, B, C, D, E and F.
Along y-axis, mark the heights of the bars (rectangles) in proportion to the given data (numbers).
Remember:
(i) The heights of different bars (rectangles) are parallel to y-axis and the mid-points of their bases are on the points marked on the x-axis (step 2).
(ii) The bars may be taken of any suitable width, but widths of all the bars must be the same.
(iii) The space (distance) between consecutive bars may be of any suitable value, but the spaces between all the consecutive bars must be the same.
The required bar graph is as given below:

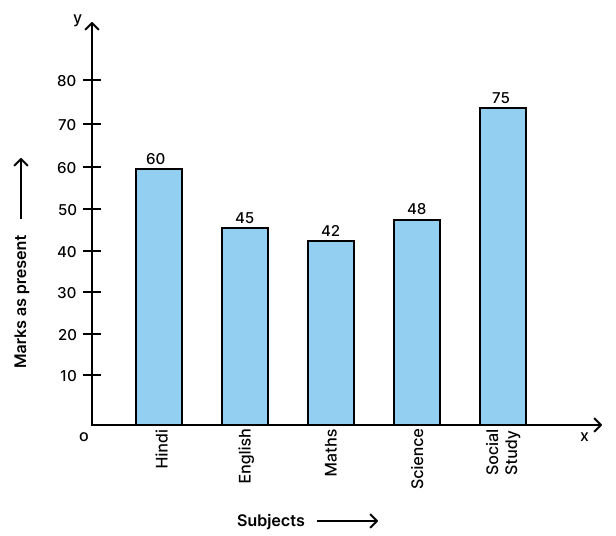
Manoj appeared for ICSE examination 2018 and secured percentage of marks as shown in the following table :
| Subjects | Hindi | English | Maths | Science | Social Study |
|---|---|---|---|---|---|
| Marks as percent | 60 | 45 | 42 | 48 | 75 |
Represent the above data by drawing a suitable bar graph.
Answer
Steps:
On a graph paper, draw two mutually perpendicular lines OX and OY which intersect each other at point O.
The line OX is taken horizontal and is called the x-axis, whereas the line OY is taken vertical and is called the y-axis.
On the x-axis, starting from O, mark points at equal distances. At these points write the names of the different subjects given. In this question, the names are Hindi, English, Maths, Science and Social Study.
Along y-axis, mark the heights of the bars (rectangles) in proportion to the given data (Marks as percent).
Remember:
(i) The heights of different bars (rectangles) are parallel to y-axis and the mid-points of their bases are on the points marked on the x-axis (step 2).
(ii) The bars may be taken of any suitable width, but widths of all the bars must be the same.
(iii) The space (distance) between consecutive bars may be of any suitable value, but the spaces between all the consecutive bars must be the same.
The required bar graph is as given below:
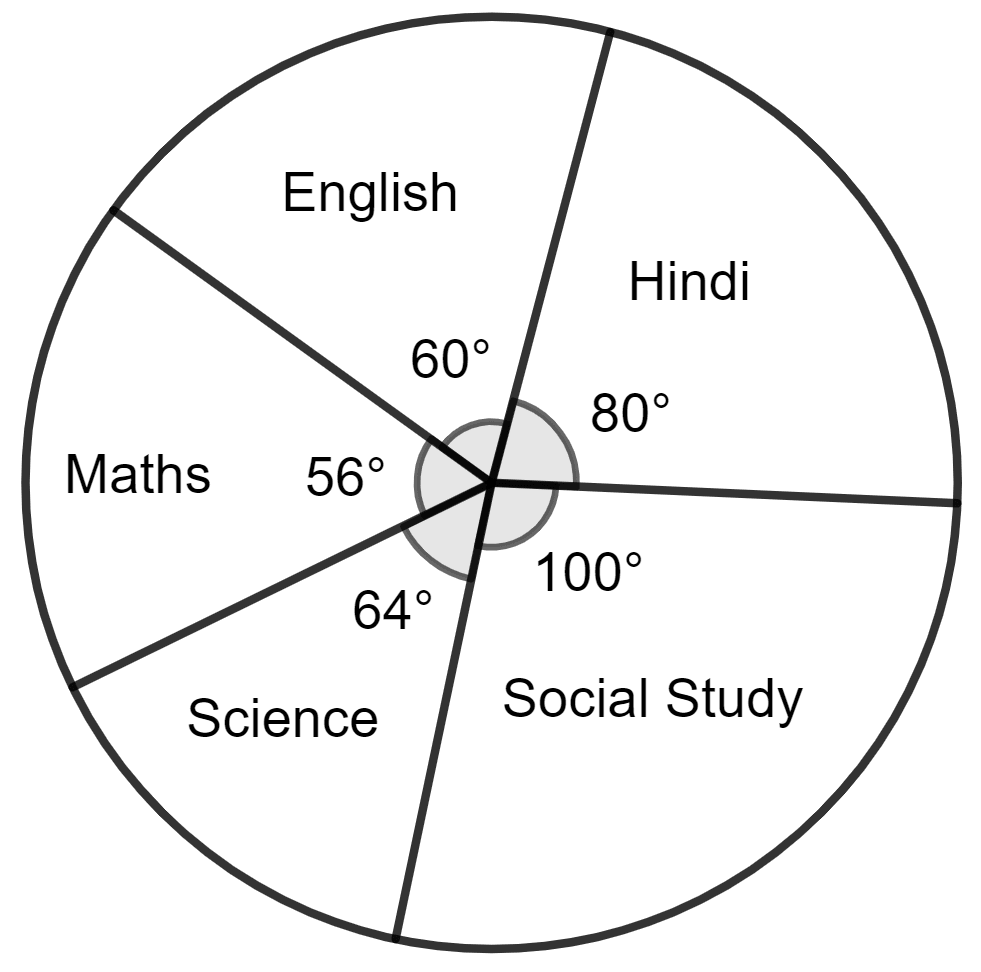
For the data given above in question number 8, draw a suitable pie-graph.
Answer
Steps:
Since the angle about the center of a circle is 360°, divide 360° in proportion to the given data. In this question, divide 360° in proportion 60 : 45 : 42 : 48 : 75 to obtain the corresponding central angles.
Make a table as given.
| Subjects | Marks as percent | Central Angles |
|---|---|---|
| Hindi | 60 | = 80° |
| English | 45 | = 60° |
| Maths | 42 | = 56° |
| Science | 48 | = 64° |
| Social Study | 75 | = 100° |
| Total | 270 | 360° |
Draw a circle of any suitable radius.
For each central-angle, draw a sector.
Mr. Kapoor compares the prices (in ₹) of different items at two different shops A and B. Examine the following table carefully and represent the data by a double bar graph.
| Items | Price (in ₹) at shop A | Price (in ₹) at shop B |
|---|---|---|
| Tea-set | 900 | 950 |
| Mixer | 700 | 800 |
| Coffee-maker | 600 | 700 |
| Dinner set | 600 | 500 |
Answer
Steps:
On a graph paper, draw two mutually perpendicular lines OX and OY which intersect each other at point O.
The line OX is taken horizontal and is called the x-axis, whereas the line OY is taken vertical and is called the y-axis.
On the x-axis, starting from O, mark points at equal distances. At these points write the names of the different items given. In this question, the names are Tea-set, Mixer, Coffee-maker and Dinner set.
Along y-axis, mark the heights of the bars (rectangles) in proportion to the given data (Prices at Shop A and B).
Remember:
(i) The heights of different bars (rectangles) are parallel to y-axis and the mid-points of their bases are on the points marked on the x-axis (step 2).
(ii) The bars may be taken of any suitable width, but widths of all the bars must be the same.
(iii) The space (distance) between consecutive bars may be of any suitable value, but the spaces between all the consecutive bars must be the same.
The required double bar graph is as given below:

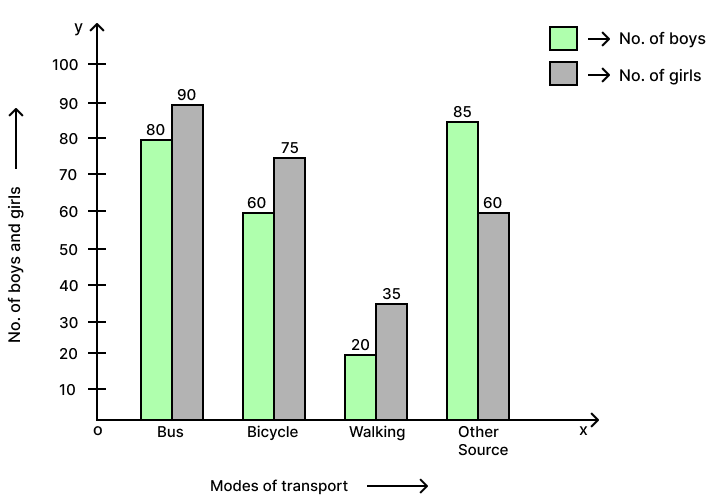
The following table shows the modes of transport used by boys and girls for going to the same school.
| Bus | Bicycle | Walking | Other sources | |
|---|---|---|---|---|
| Number of boys | 80 | 60 | 20 | 85 |
| Number of girls | 90 | 75 | 35 | 60 |
Draw a double bar graph representing the above data.
Answer
Steps:
On a graph paper, draw two mutually perpendicular lines OX and OY which intersect each other at point O.
The line OX is taken horizontal and is called the x-axis, whereas the line OY is taken vertical and is called the y-axis.
On the x-axis, starting from O, mark points at equal distances. At these points write the names of the modes of transport given. In this question, the names are Bus, Bicycle, Walking and Other sources.
Along y-axis, mark the heights of the bars (rectangles) in proportion to the given data (Number of boys and girls).
Remember:
(i) The heights of different bars (rectangles) are parallel to y-axis and the mid-points of their bases are on the points marked on the x-axis (step 2).
(ii) The bars may be taken of any suitable width, but widths of all the bars must be the same.
(iii) The space (distance) between consecutive bars may be of any suitable value, but the spaces between all the consecutive bars must be the same.
The required double bar graph is as given below:
The number of times a data, in the set, occurs is called :
upper-limit
class-mark
frequency
class-limit
Answer
Frequency refers to the number of times a particular data value appears in a dataset.
Hence, option 3 is the correct option.
The difference between the greatest and the smallest values of observations is called :
frequency
range
class-mark
class-limit
Answer
Range refers to the difference between the highest and lowest values of observation.
Hence, option 2 is the correct option.
The difference between the upper and lower class-limits of a class-interval is called :
width of the class-interval
frequency
class-limit
class-mark
Answer
The difference between the upper and lower class-limits of a class-interval is called width of the class-interval.
Hence, option 1 is the correct option.
In a bar-graph, if the widths of all the bars are kept same, their heights are proportional to their :
class-size
class-mark
class-limits
frequency
Answer
In a bar-graph, if the widths of all the bars are kept same, their heights are proportional to their frequency.
Hence, option 4 is the correct option.
In a pie-chart, the angle corresponding to different components is :
total value of all the components x value of the component x 360°
Answer
In a pie-chart, the angle corresponding to different components is .
Hence, option 3 is the correct option.
Consider the following class intervals of a grouped data :
| Class interval | 10-25 | 25-40 | ------- | 55-70 |
|---|
Statement 1: Class marks of the 3rd class intervals is 46.5.
Statement 2: If the class mark of 2nd interval is 77.5, the interval is 60 - 85.
Which of the following options is correct?
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Answer
Given,
| Class interval | 10-25 | 25-40 | ------- | 55-70 |
|---|
3rd class interval = 40 - 55
By formula,
Class mark =
=
=
= 47.5
So, statement 1 is false.
The class mark of 2nd interval = 77.5.
Let the interval be x - y.
We know that,
The width of the every interval is 15.
⇒ y - x = 15 ................(2)
Adding equation (1) and (2), we get :
⇒ (x + y) + (y - x) = 155 + 15
⇒ x + y + y - x = 170
⇒ 2y = 170
⇒ y =
⇒ y = 85.
Substituting the value of y in equation (1), we get :
⇒ x + 85 = 155
⇒ x = 155 - 85
⇒ x = 70.
Thus, interval is 70 - 85.
So, statement 2 is false.
∴ Both the statements are false.
Hence, option 2 is the correct option.
Assertion (A) : If in a pie chart representing the number of students of opting for different streams in college admission out of a total admissions of 3300, the central angle for the sector representing mathematics is 48°, then the number of students who opt for mathematics is 440.
Reason (R) : Central angle for sector (Component) =
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
Given, total admissions = 3300
The central angle for the sector representing mathematics = 48°
By formula,
Central angle for sector (Component) =
Substituting the values,
So, assertion (A) is true.
∴ Both A and R are correct, and R is the correct explanation for A.
Hence, option 1 is the correct option.
Assertion (A) : Class size of the following class intervals is 10.
1 - 10, 11 - 20, 21 - 30, etc.
Reason (R) : The difference between the upper limit and lower limit is the class size.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
Given, the class intervals -
1 - 10, 11 - 20, 21 - 30, etc.
As we know that class size is the difference between upper and lower limits.
Class size = Upper limit - Lower limit
So, reason (R) is true.
1st class interval: 1 - 10
Class size = 10 - 1 = 9
2nd class interval: 11 - 20
Class size = 20 - 11 = 9
So, assertion (A) is false.
∴ A is false, but R is true.
Hence, option 4 is the correct option.
Assertion (A) : The given bar graph shows the heights of six mountain peaks.
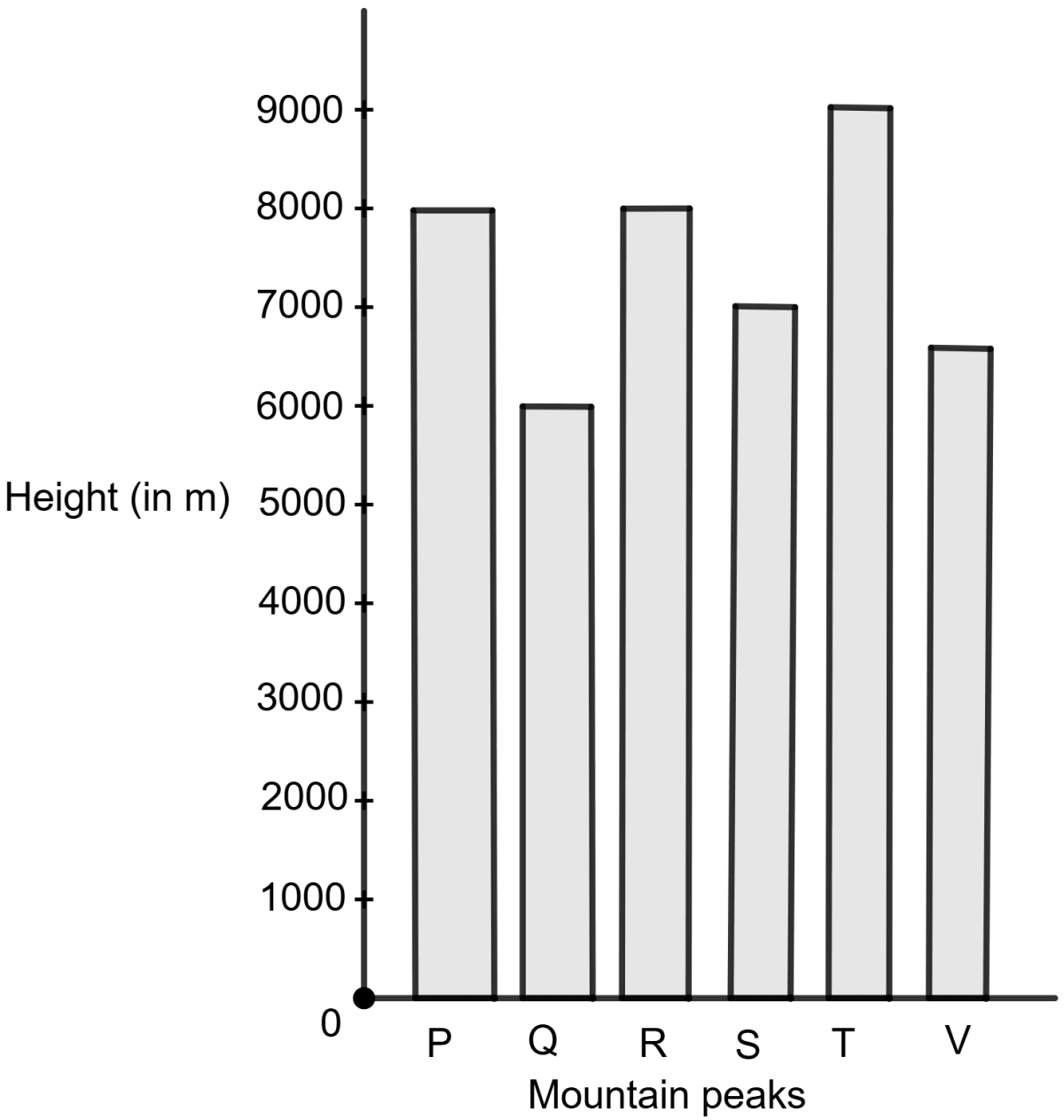
The ratio of height of the highest to the lowest peak is 3 : 2.
Reason (R) : The space between consecutive bars may be of any suitable value, but the spaces between all the consecutive bars must the same.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
Height of highest peak = 9000 m
Height of lowest peak = 6000 m
Ratio of height = 9000 : 6000 = 9 : 6 = 3 : 2.
So, assertion (A) is true.
In bar graph,
The space between consecutive bars may be of any suitable value, but the spaces between all the consecutive bars must the same.
So, reason (R) is true.
∴ Both A and R are correct, and R is not the correct explanation for A.
Hence, option 2 is the correct option.
Assertion (A) : The distribution of land in Pacific Housing Society is shown in the pie chart below. The total land area for project is 144000 m2.
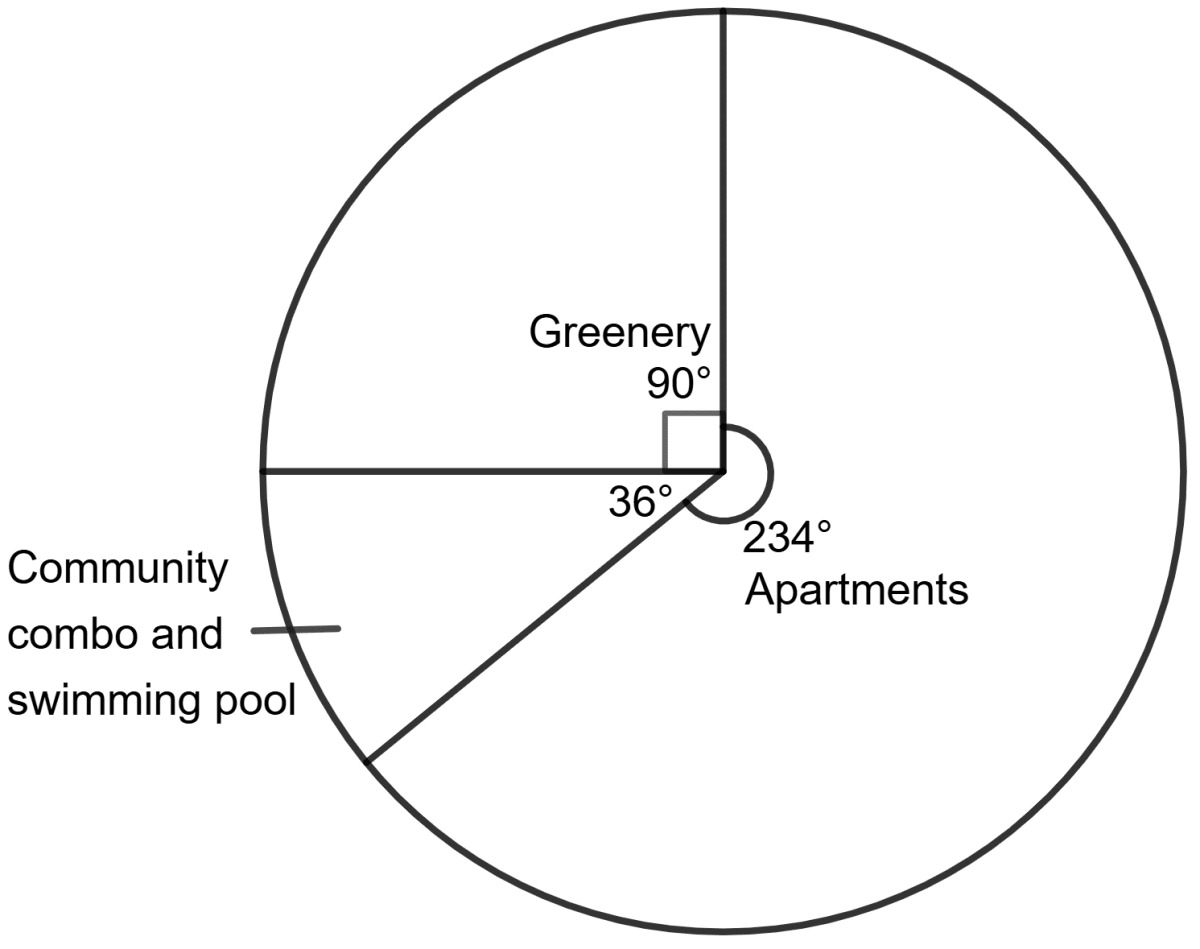
The ratio of the area kept open to the ratio of the area for apartment construction is 5 : 13.
Reason (R) : In a pie chart, the central angle of a sector suspended by its arc is proportional to the value it represents.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are incorrect.
A is true, but R is false.
A is false, but R is true.
Answer
In a pie chart, the central angle of a sector suspended by its arc is proportional to the value it represents.
So, reason (R) is true.
Area kept open =
Area for apartment construction =
So, assertion (A) is true.
∴ Both A and R are correct, and R is the correct explanation for A.
Hence, option 1 is the correct option.
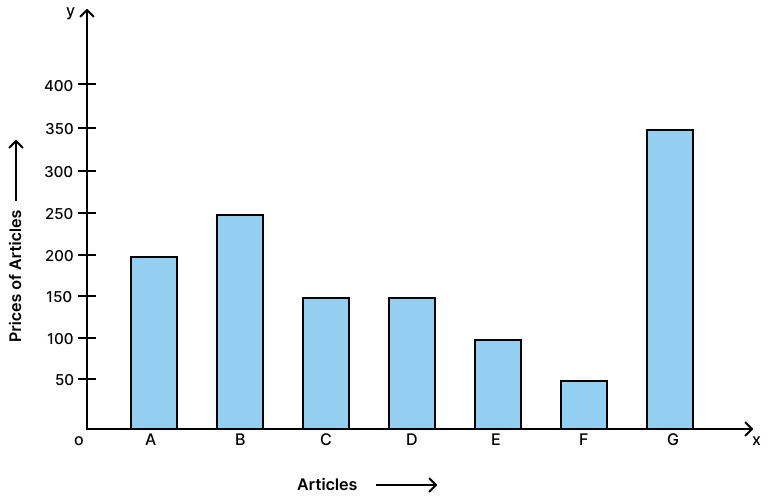
Draw a bar-graph to represent the following data :
| Articles : | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| Price of articles : | 200 | 250 | 150 | 150 | 100 | 50 | 350 |
Answer
Steps:
On a graph paper, draw two mutually perpendicular lines OX and OY which intersect each other at point O.
The line OX is taken horizontal and is called the x-axis, whereas the line OY is taken vertical and is called the y-axis.
On the x-axis, starting from O, mark points at equal distances. At these points write the names of the different articles given. In this question, the names are A, B, C, D, E, F and G.
Along y-axis, mark the heights of the bars (rectangles) in proportion to the given data (Prices of articles).
Remember:
(i) The heights of different bars (rectangles) are parallel to y-axis and the mid-points of their bases are on the points marked on the x-axis (step 2).
(ii) The bars may be taken of any suitable width, but widths of all the bars must be the same.
(iii) The space (distance) between consecutive bars may be of any suitable value, but the spaces between all the consecutive bars must be the same.
The required bar graph is as given below:
Study the given graph and then answer the following questions :
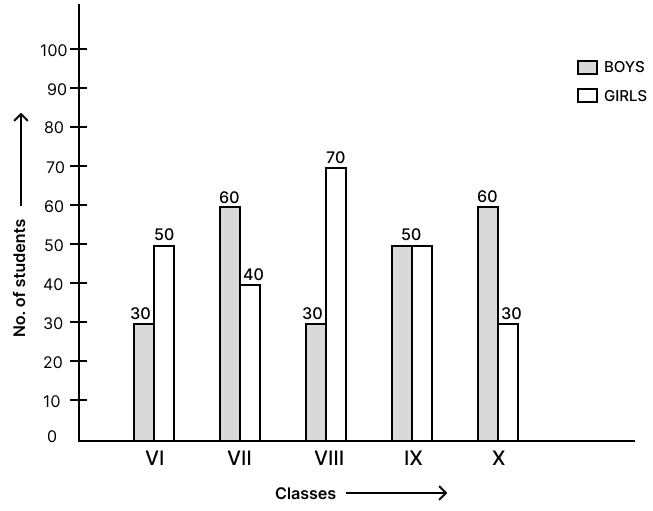
(i) Which classes have the larger number of students ?
(ii) Which class has the equal number of girls and boys ?
(iii) What is the total number of students in class VIII ?
(iv) What is the total number of students (from the class VI to class X) ?
Answer
(i) Numbers of students in VI = Number of boys + Number of girls
= 30 + 50 = 80
Numbers of students in VII = Number of boys + Number of girls
= 60 + 40 = 100
Numbers of students in VIII = Number of boys + Number of girls
= 30 + 70 = 100
Numbers of students in IX = Number of boys + Number of girls
= 50 + 50 = 100
Numbers of students in X = Number of boys + Number of girls
= 60 + 30 = 90
Hence, classes VII, VIII and IX have the larger number of students.
(ii) In class IX, the number of boys = number of girls = 50.
Hence, class IX has an equal number of girls and boys.
(iii) Numbers of students in VIII = Number of boys + Number of girls
= 30 + 70
= 100
Hence, the total number of students in class VIII is 100.
(iv) Total number of students = Number of students in class VI + Number of students in class VII + Number of students in class VIII + Number of students in class IX + Number of students in class X
= 80 + 100 + 100 + 100 + 90
= 470
Hence, the total number of students from class VI to X is 470.
The following table shows the number of students in various classes :
| Class | VI | VII | VIII | IX | X |
|---|---|---|---|---|---|
| No. of students | 360 | 300 | 54 | 150 | 216 |
Draw a pie-graph to represent the above data.
Answer
Steps:
Since the angle about the center of a circle is 360°, divide 360° in proportion to the given data. In this question, divide 360° in proportion 360 : 300 : 54 : 150 : 216 to obtain the corresponding central angles.
Make a table as given.
| Class | No. of students | Central Angles |
|---|---|---|
| VI | 360 | = 120° |
| VII | 300 | = 100° |
| VIII | 54 | = 18° |
| IX | 150 | = 50° |
| X | 216 | = 72° |
| Total | 1,080 | 360° |
Draw a circle of any suitable radius.
For each central-angle, draw a sector.
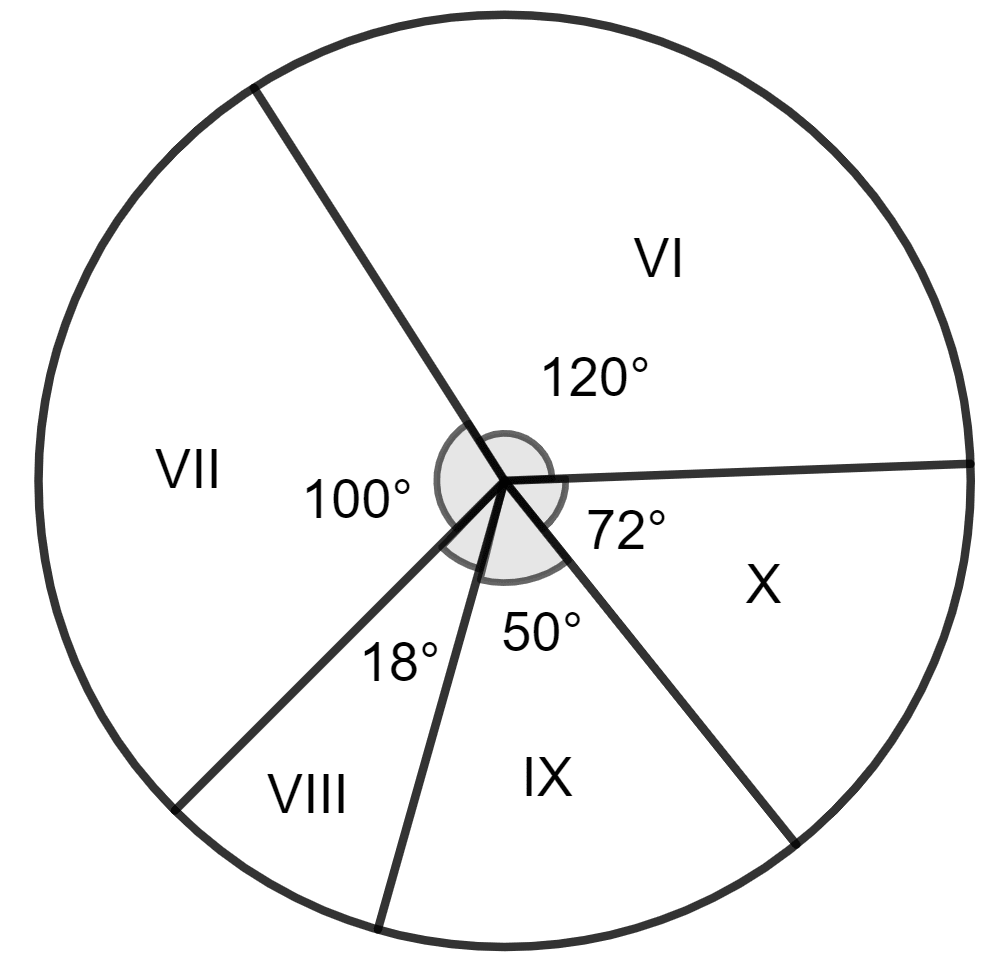
The given pie-graph represents the number of students in different classes. If the total of all the students in the class is 1080; use the graph to find the number of students in each class.
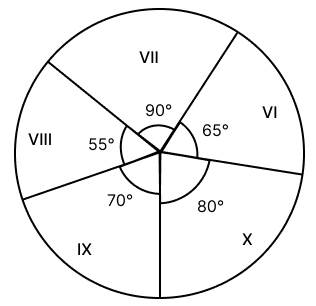
Answer
Given:
Total number of students = 1,080
| Class | No. of students (°) | No. of students |
|---|---|---|
| VI | 65° | = 195 |
| VII | 90° | = 270 |
| VIII | 55° | = 165 |
| IX | 70° | = 210 |
| X | 80° | = 240 |
Hence, the number of students in each class is as follows:
Class VI: 195 students
Class VII: 270 students
Class VIII: 165 students
Class IX: 210 students
Class X: 240 students