Physics
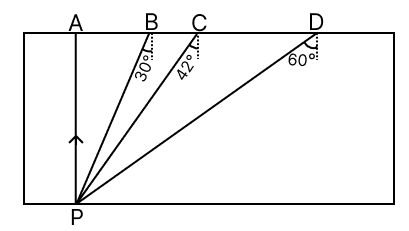
The adjacent diagram represents a glass slab of refractive index 1.5. If PA, PB, PC and PD represent the rays of light from a point P at the bottom of the block, draw the approximate directions of these rays as they emerge out of the glass slab. (sin 42° = 2/3)
Refraction Plane Surfaces
1 Like
Answer
Given,
Refractive index of glass with respect to air = aμg = 1.5 =
Angle made by PA with normal = 0°
Angle made by PB with normal = 30°
Angle made by PC with normal = 42°
Angle made by PD with normal = 60°
sin 42° = 2/3
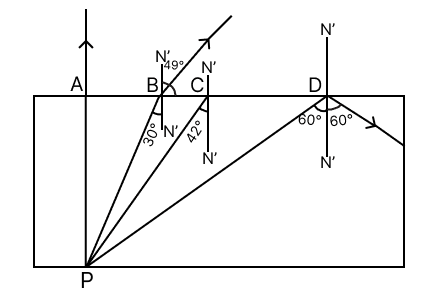
(i) For ray PA
i = 0°
⟹ r = sin-1(0) = 0°
Ray PA will not deviate and emerge straight.
(ii) For PB
i = 30°
⟹ r = sin-1(0.75) ≈ 49°
Ray PB will emerge at an angle of 49° with the normal.
(iii) For PC
i = 42°
⟹ r = sin-1(1) = 90°
This is the condition for critical angle.
Ray PC will graze along the surface.
(iv) For PD
i = 60°
Here,
sin r > 1 which a condition of total internal reflection.
Ray PD will suffer total internal reflection.
Answered By
2 Likes
Related Questions
The figure given below shows a radioactive nucleus A composed of 84 protons and 128 neutrons kept in a thick lead walled container. The emitted particles pass through a magnetic field in a direction perpendicular to the plane of paper inwards as shown by X. The nucleus A emits a particle which deflects to the left and is transformed into nucleus B. Nucleus B further emits a particle which deflects towards right and transforms into nucleus C.
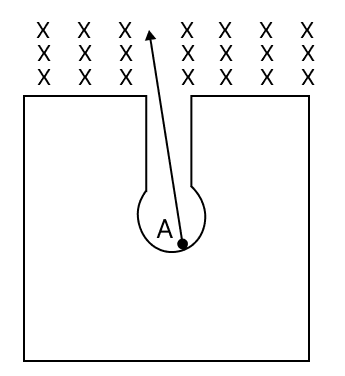
(a) Name the radiations emitted by nucleus A and B.
(b) Name the law used to identify the radiations.
(c) What is the composition of nucleus C?
Jatin puts a pencil into a glass container having water and is surprised to see the pencil in a different state.

(a) What change is observed in the appearance of the pencil?
(b) What is the reason for this change?
(c) Classify the following as a real or virtual image:
The image of a candle flame formed on a screen by a convex lens.The figure given below shows the experimental set up for the determination of focal length of a lens using a plane mirror.

(a) Draw two rays from the point O of the object to show the formation of image I at O itself.
(b) What is the size of the image I?
(c) A convex lens of short focal length is used in which optical instrument?
(d) The focal length of a convex lens is 25 cm. Express its power with sign.
A lens of focal length 15 cm forms an erect image three times the size of the object on a screen.
(a) What kind of lens is this?
(b) Find the position of the object from the lens.
(c) Find the position of the screen from the lens.