Physics
A lens of focal length 15 cm forms an erect image three times the size of the object on a screen.
(a) What kind of lens is this?
(b) Find the position of the object from the lens.
(c) Find the position of the screen from the lens.
Refraction Lens
2 Likes
Answer
Given,
Focal length of the lens (f) = 15cm
Magnification of the lens (m) = +3 ∵ (image formed is virtual and erect)
(a) This is a convex lens because only convex lens forms a magnified image when the object is between the lens and the focus.
(b) Let,
Distance of object from the lens = u
Distance of image from the lens = v
As for lens,
⇒ v = 3u ………. (1)
From lens formula,
On putting values
The object is placed 10 cm in front of the lens.
(c) From (1)
Distance of the screen from the lens = image distance (v) = -30 cm
The screen is placed 30 cm in front of the lens.
Answered By
1 Like
Related Questions
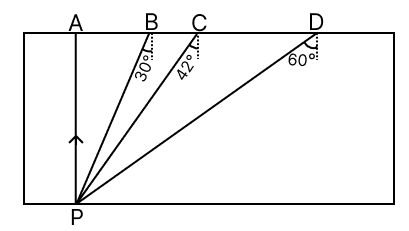
The adjacent diagram represents a glass slab of refractive index 1.5. If PA, PB, PC and PD represent the rays of light from a point P at the bottom of the block, draw the approximate directions of these rays as they emerge out of the glass slab. (sin 42° = 2/3)
The figure given below shows the experimental set up for the determination of focal length of a lens using a plane mirror.

(a) Draw two rays from the point O of the object to show the formation of image I at O itself.
(b) What is the size of the image I?
(c) A convex lens of short focal length is used in which optical instrument?
(d) The focal length of a convex lens is 25 cm. Express its power with sign.
The diagram given below shows a ray of blue, yellow and red light incident on one face of a prism.
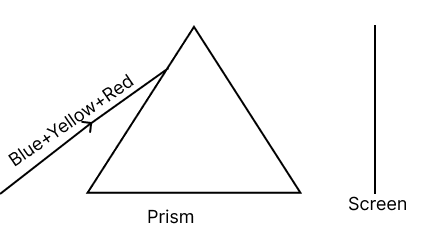
(a) Complete the diagram to show the effect of the prism on the ray of light and to show what is seen on the screen.
(b) A slit is placed in between the prism and the screen to pass yellow light only. What will be your observation on the screen ?
(c) What conclusion do you draw from the observation in part (ii) above ?
In the figure given below, a ray of light PQ is incident normally on the face AB of an equilateral glass prism. Complete the ray diagram showing its emergence into air after passing through the prism. Take critical angle for glass = 42°
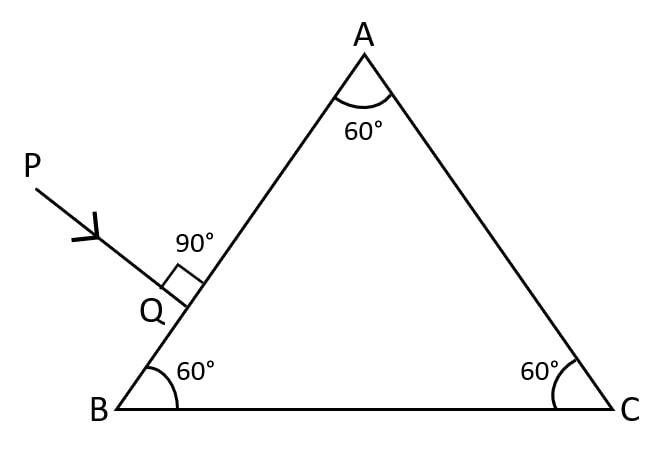
(a) Write the angles of incidence at the faces AB and AC of the prism.
(b) Name the phenomenon suffered by the ray of light at the face AB, AC and BC of the prism respectively.