Mathematics
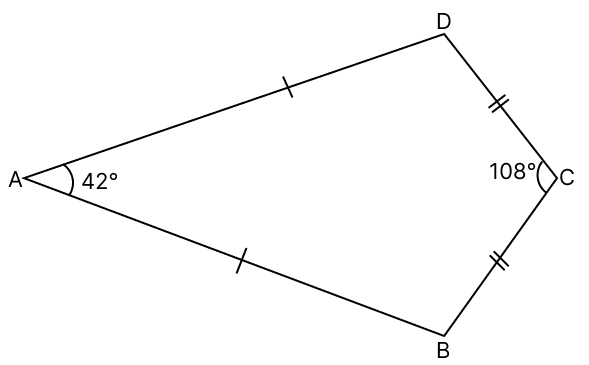
In the given figure, AB = AD; CB = CD; ∠A = 42° and ∠C = 108°, find ∠ABC.
Triangles
3 Likes
Answer
Join BD.
In △ABD,
AB = AD
⇒ ∠ABD = ∠ADB = x (let) (Angles opposite to equal sides in a triangle are equal)
By angle sum property of triangle,
⇒ ∠BAD + ∠ABD + ∠ADB = 180°
⇒ 42° + x + x = 180°
⇒ 2x = 180° - 42°
⇒ 2x = 138°
⇒ x =
⇒ x = 69°
⇒ ∠ABD = ∠ADB = 69°.
In △BCD,
CB = CD
⇒ ∠CBD = ∠CDB = y (let) (Angles opposite to equal sides in a triangle are equal)
By angle sum property of triangle,
⇒ ∠BCD + ∠CBD + ∠CDB = 180°
⇒ 108° + y + y = 180°
⇒ 2y = 180° - 108°
⇒ 2y = 72°
⇒ y =
⇒ y = 36°
⇒ ∠CBD = ∠CDB = 36°
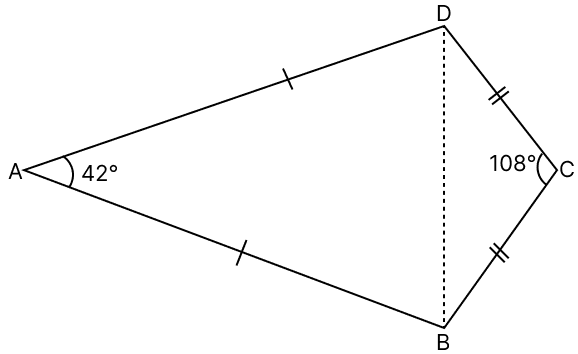
From figure,
∠ABC = ∠ABD + ∠CBD = 69° + 36° = 105°.
Hence, ∠ABC = 105°.
Answered By
1 Like
Related Questions
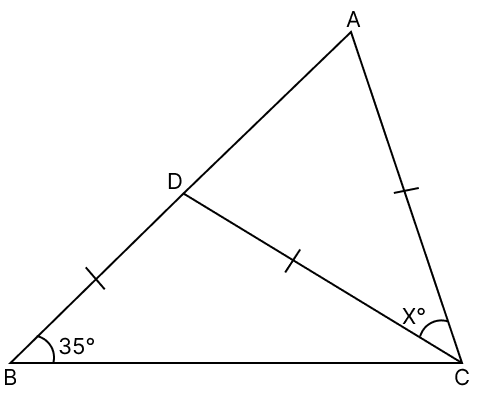
In the given figure, CA = CD = BD; ∠DBC = 35° and ∠DCA = x°. Find the value of x.
In the given figure, △ABC is an equilateral triangle whose base BC is produced to D such that BC = CD. Calculate :
(i) ∠ACD
(ii) ∠ADC
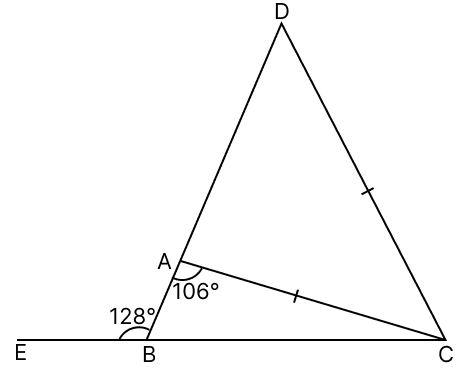
In the given figure, side BA of △ABC has been produced to D such that CD = CA and side CB has been produced to E. If ∠BAC = 106° and ∠ABE = 128°, find ∠BCD.
In the given figure, AB = BC and AC = CD. Show that: ∠BAD : ∠ADB = 3 : 1