Mathematics
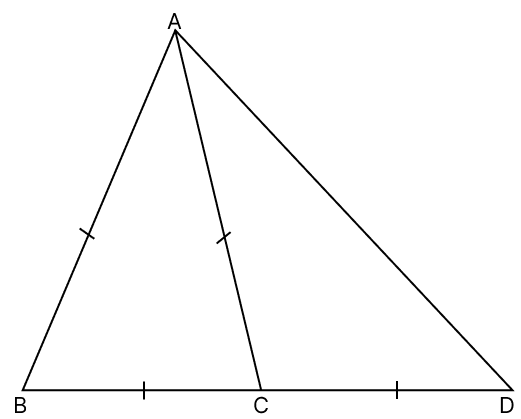
In the given figure, △ABC is an equilateral triangle and BC is produced to D such that BC = CD. Prove that AD ⊥ AB.
Triangles
1 Like
Answer
Given,
△ABC is an equilateral triangle.
⇒ ∠ABC = ∠ACB = ∠BAC = 60°
From figure,
⇒ ∠ACB + ∠ACD = 180° (Linear pair)
⇒ 60° + ∠ACD = 180°
⇒ ∠ACD = 180° - 60°
⇒ ∠ACD = 120°.
In △CAD,
CA = CD (As, BC = CD and BC = CA)
⇒ ∠CAD = ∠CDA = x (let) (Angles opposite to equal sides are equal)
By angle sum property of triangle,
⇒ ∠CAD + ∠CDA + ∠ACD = 180°
⇒ x + x + 120° = 180°
⇒ 2x = 180° - 120°
⇒ 2x = 60°
⇒ x =
⇒ x = 30°
⇒ ∠CAD = ∠CDA = 30°
From figure,
⇒ ∠BAD = ∠BAC + ∠CAD = 60° + 30° = 90°.
Hence, proved that AD ⊥ AB.
Answered By
2 Likes
Related Questions
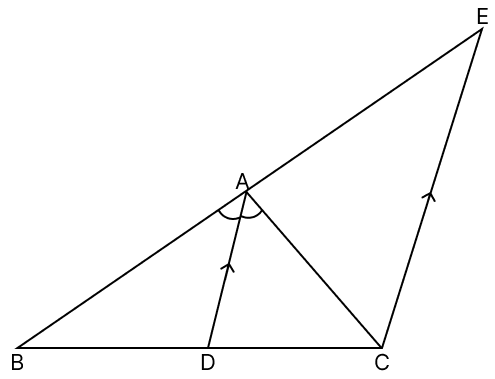
In the given figure, AD is the internal bisector of ∠A and CE || DA. If CE meets BA produced at E, prove that △CAE is isosceles.
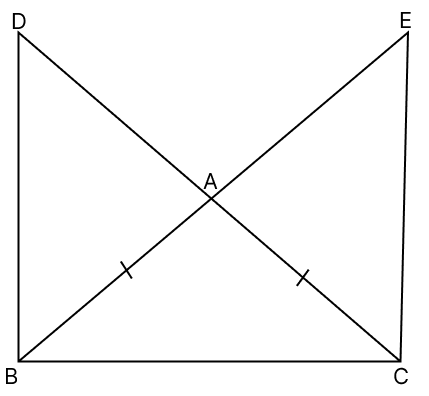
In the adjoining figure, AB = AC. If DB ⊥ BC and EC ⊥ BC, prove that :
(i) BD = CE
(ii) AD = AE
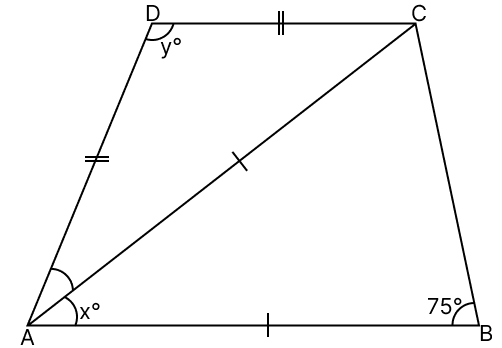
In the given figure, AC is the bisector of ∠A. If AB = AC, AD = CD and ∠ABC = 75°, find the values of x and y.
In a △PQR, ∠P = 50° and ∠R = 70°. Name :
(i) the shortest side
(ii) the longest side of the triangle