Mathematics
In the given figure, the bisectors of ∠B and ∠C intersect each other at O and ∠BAC = 50°. The measure of ∠BOC is :
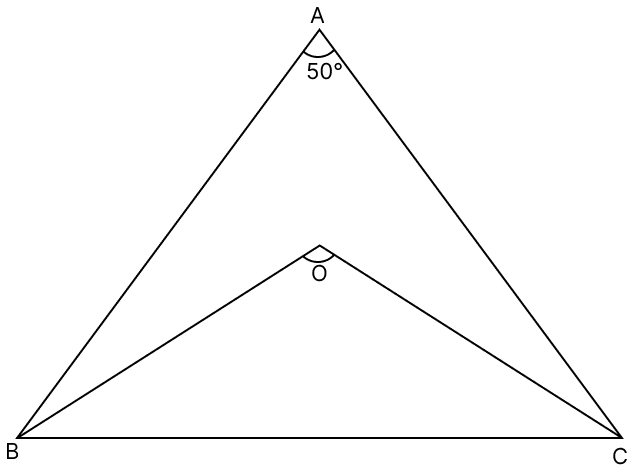
100°
115°
130°
140°
Triangles
2 Likes
Answer
In △ABC,
By angle sum property of triangle,
∠A + ∠B + ∠C = 180°
⇒ 50° + ∠B + ∠C = 180°
⇒ ∠B + ∠C = 180° - 50°
⇒ ∠B + ∠C = 130° …….(1)
From figure,
As, OB is bisector of angle B.
∠B = ∠ABO + ∠OBC = ∠OBC + ∠OBC = 2∠OBC
⇒ ∠OBC =
As, OC is bisector of angle C.
∠C = ∠ACO + ∠OCB = ∠OCB + ∠OCB = 2∠OCB
⇒ ∠OCB =
In △OBC,
By angle sum property of triangle,
⇒ ∠OBC + ∠BOC + ∠OCB = 180°
⇒ + ∠BOC + = 180°
⇒ ∠BOC + = 180°
⇒ ∠BOC + = 180° [Substituting from eq.(1)]
⇒ ∠BOC + 65° = 180°
⇒ ∠BOC = 180° - 65°
⇒ ∠BOC = 115°.
Hence, option 2 is the correct option.
Answered By
3 Likes
Related Questions
Assertion (A): If three angles of a triangle are equal to the corresponding three angles of another triangle, then the triangles are congruent.
Reason (R): Two triangles are said to be congruent, if and only if, one of them can be made to superimpose on the other so as to cover exactly.
A is true, R is false
A is false, R is true
Both A and R are true
Both A and R are false
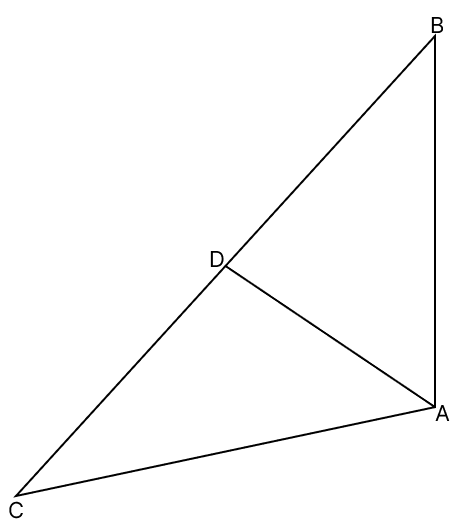
Assertion (A): In △ABC, D is a point on side BC. AB + BC + AC > 2AD
Reason (R): Sum of two sides of a triangle is greater than the third side.
A is true, R is false
A is false, R is true
Both A and R are true
Both A and R are false
In the given figure, △ABD ≅ △ACD. If ∠DAC = 30° and ∠BDC = 110°, then the measure of ∠DBA is :
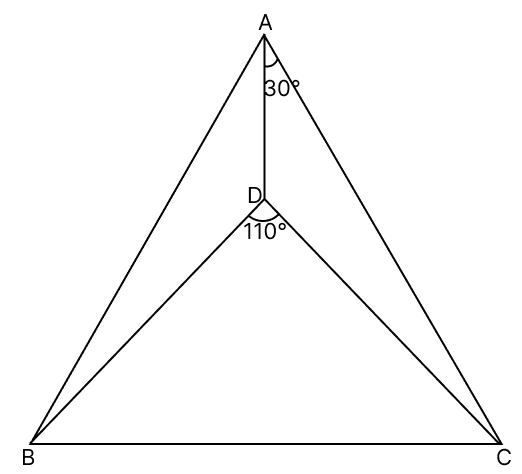
30°
50°
70°
25°
ABC is a triangle in which AC = BC and ∠BAC = 50°. Side BC is produced to D such that BC = CD. ∠BAD is equal to :
45°
50°
90°
100°