In an isosceles triangle, prove that the altitude from the vertex bisects the base.

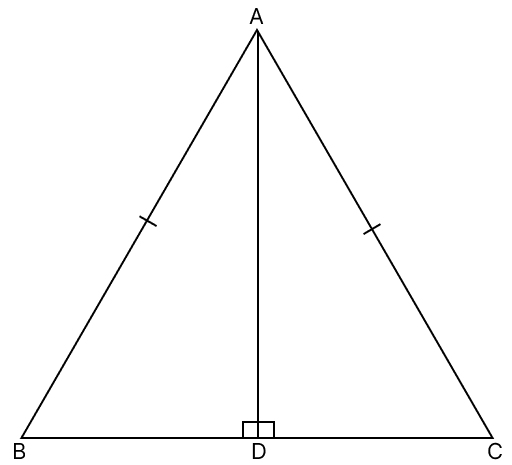
Let ABC be an isosceles triangle with AB = AC.

Let AD be a perpendicular from vertex A to base BC.

In △ADB and △ADC,

⇒ AD = AD (Common side)

⇒ AB = AC (Given)

⇒ ∠ADB = ∠ADC (Each equal to 90°)

∴ △ADB ≅ △ADC (By R.H.S axiom)

∴ DB = DC (Corresponding parts of congruent triangles are equal)

Hence, proved that the altitude from the vertex in an isosceles triangle bisects the base.