Mathematics
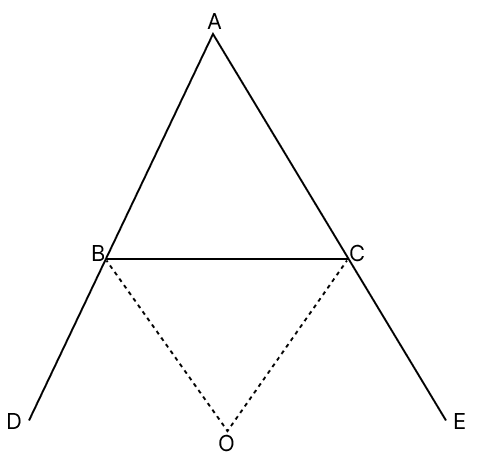
The sides AB and AC of △ABC are produced to D and E respectively and the bisectors of ∠CBD and ∠BCE meet at O. If AB > AC, prove that OC > OB.
Triangles
3 Likes
Answer
In △ABC,
AB > AC
⇒ ∠ACB > ∠ABC
∠ACB + ∠BCE = 180° …..(1) [Linear pair]
∠ABC + ∠CBD = 180° …..(2) [Linear pair]
Adding eq.(1) and (2), we have:
∠ACB + ∠BCE = ∠ABC + ∠CBD
Since, ∠ACB > ∠ABC
⇒ ∠BCE < ∠CBD
⇒ ∠BCE < ∠CBD
⇒ ∠BCO < ∠CBO
⇒ ∠CBO > ∠BCO
∴ OC > OB.
Hence, proved that OC > OB.
Answered By
1 Like
Related Questions
If O is any point inside △ABC, prove that ∠BOC > ∠A.
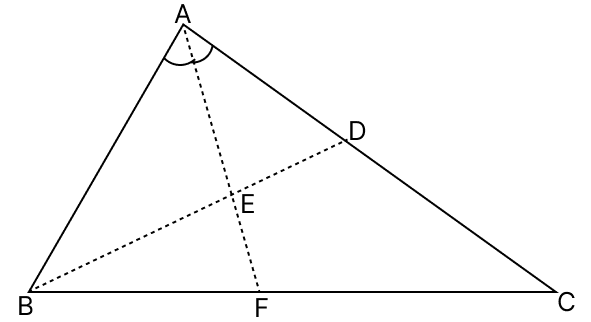
In the given figure, AD = AB and AE bisects ∠A. Prove that:
(i) BE = ED
(ii) ∠ABD > ∠BCA
In △ABC, AB = 7.5 cm, BC = 6.2 cm and AC = 5.4 cm. Name :
(i) the least angle
(ii) the greatest angle of the triangle
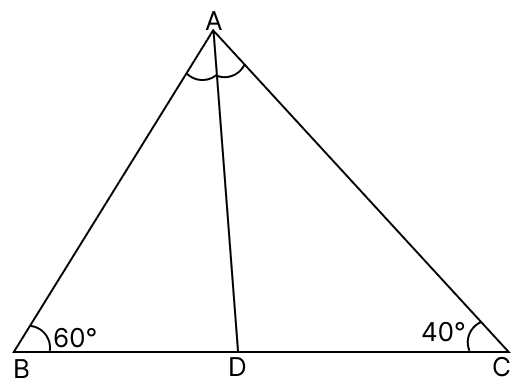
In the given figure, AD bisects ∠A. If ∠B = 60°, ∠C = 40°, then arrange AB, BD and DC in ascending order of their lengths.