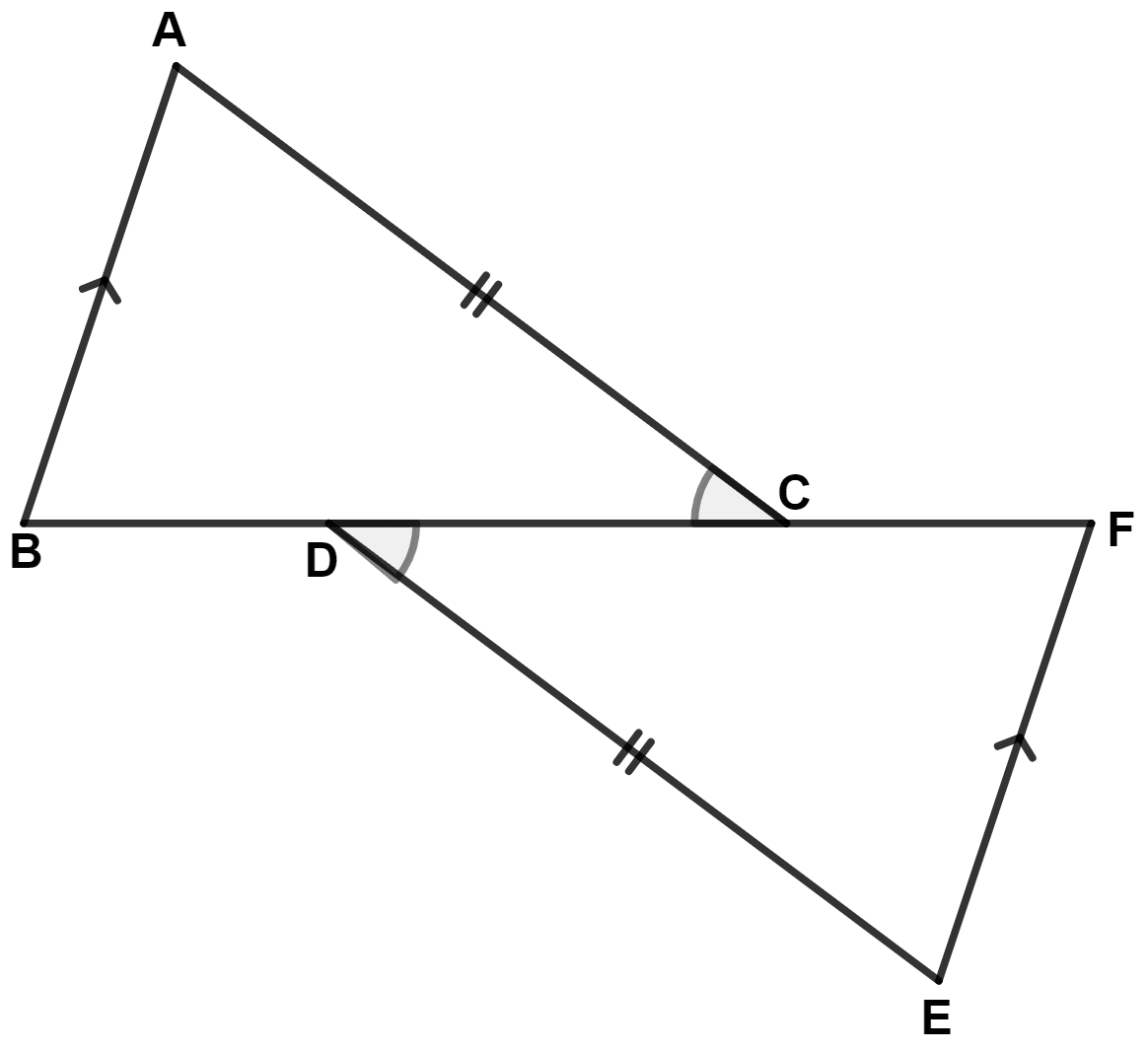
Use the information in the given figure, to prove :

(i) AB = FE

(ii) BD = CF.

(i) In △ ABC and △ EFD,

⇒ AC = DE (Given)

⇒ ∠ABC = ∠EFD (Alternate angles are equal)

⇒ ∠ACB = ∠EDF (Given)

∴ ∆ ABC ≅ ∆ EFD (By A.A.S. axiom)

We know that,

Corresponding parts of congruent triangles are equal.

∴ AB = FE.

Hence, proved that AB = FE.

(ii) Since, ∆ ABC ≅ ∆ EFD,

∴ BC = FD …….(By C.P.C.T.C.)

Subtracting CD from both sides, we get :

⇒ BC - CD = FD - CD

⇒ BD = CF.

Hence, proved that BD = CF.