In the given figure, AB is the largest chord of the circle, AB = 18 cm and the length of the chord CD is half of length of chord AB, then :
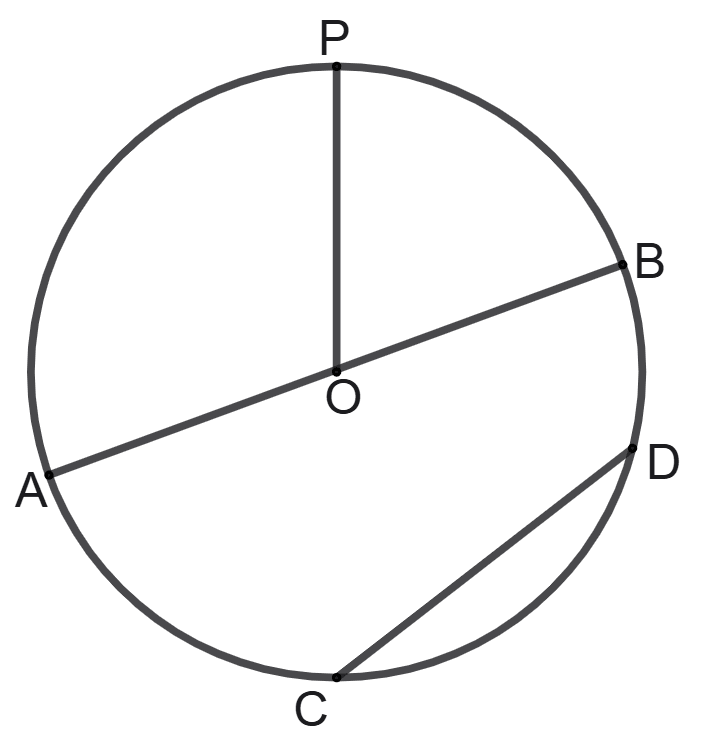
OP = 18 cm and CD = 18 cm
OP = 9 cm and CD = 18 cm
OP = 18 cm and CD = 9 cm
OP = 9 cm and CD = 9 cm
Answer
As we know that
the largest chord of a circle is its diameter.
Diameter, AB = 20 cm
Chord CD = half of length of chord AB =
= 9 cm.
OP is radius of the circle. So, radius is half of the diameter.
OP = = 9 cm
∴ OP = 9 cm and CD = 9 cm
Hence, option 4 is the correct option.
The largest chord of a circle is 20 cm, then its radius is :
20 cm
40 cm
10 cm
none of these
Answer
The largest chord of a circle is its diameter.
∴ Diameter = 20 cm
As we know that radius is half of the diameter.
Radius = = 10 cm
Hence, option 3 is the correct option.
The relation between the area enclosed by a major segment of a circle and area enclosed by its semi-circle is :
major segment is smaller than the semi-circle.
major segment is bigger than the semi-circle.
major segment is equal to the semi-circle.
Answer
The central angle θ for the major segment is greater than 180°, leading to a larger sector area, and consequently, a larger segment area.
∴ Major segment is bigger than the semi-circle.
Hence, option 2 is the correct option.
The radius of a circle is 5 cm then the length of its longest chord is :
less than 5 cm.
equal to 5 cm.
equal to 10 cm.
less than 10 cm
Answer
Given, radius of a circle = 5 cm.
The largest chord of a circle is its diameter.
As we know that radius is half of the diameter.
⇒ Diameter = 2 x radius = 2 x 5 cm = 10 cm
∴ Length of its longest chord = 10 cm
Hence, option 3 is the correct option.
The diameter of a circle with centre at point O is 30 cm. A point P lies in the same plane as the circle and OP = 20 cm, then point P lies :
on the circumference of the circle
inside the circle.
outside the circle.
nothing can be said
Answer
Given, diameter of a circle = 30 cm.
As we know that radius is half of the diameter.
⇒ Radius = x diameter= x 30
= 15 cm.
The distance from the center O to point P is 20 cm. Since OP = 20 cm is greater than the radius of the circle (15 cm).
∴ Point P lies outside the circle.
Hence, option 3 is the correct option.
The angle between a line AB and the diameter of a circle is 90°; line AB is :
a tangent of the circle
not a tangent of the circle
nothing can be said
Answer
The angle between a line AB and the diameter of a circle is 90°; line AB can be either a tangent of the circle or cannot be a tangent of the circle.
Thus, nothing can be confirmed.
Hence, option 3 is the correct option.
A sector of a circle can be equal to its segment :
yes
no
none of these two
Answer
A segment of a circle is the area bounded by a chord of a circle and the area of the circle between the two endpoints of the chord.
A sector of a circle is a portion of a circle created by the arc of the circle and two radii.
∴ A sector of a circle can be equal to a segment of the same circle when the sector is a semicircle.
Yes, a sector of a circle can be equal to its segment.
Hence, option 1 is the correct option.
The given figure shows a circle with center O. If length of arc AQC is double of arc APB and ∠AOB = 65°; then angle AOC is :
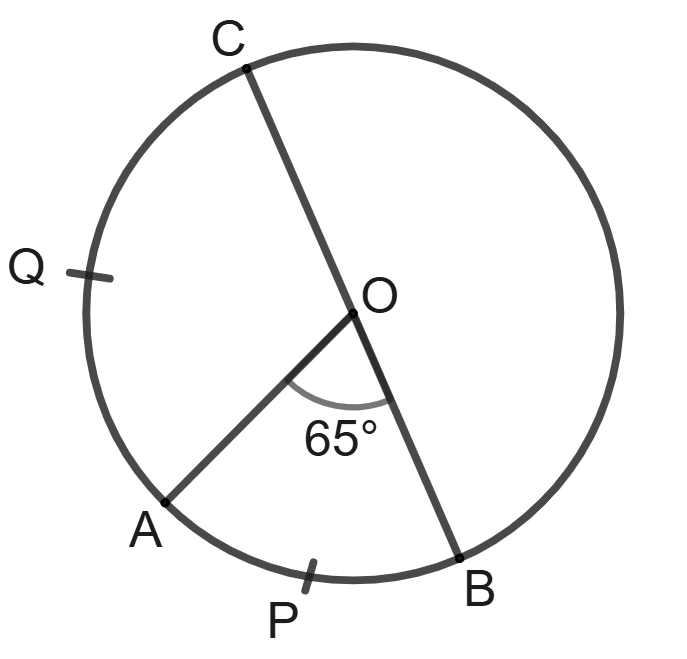
65°
2 x 65°
X 65°
none of these
Answer
Given, length of arc AQC is double of arc APB.
If arc AQC is twice the length of arc APB, then the angle subtended by arc AQC at the center (∠AOC) will also be twice the angle subtended by arc APB (∠AOB).
∴ ∠AOC = 2 x ∠AOB.
⇒ ∠AOC = 2 x 65°
⇒ ∠AOC = 130°.
Hence, option 2 is the correct option.
Statement 1: The angle between a radius and tangent of a circle is 90°.
Statement 2: At the point of contact the angle between radius and tangent is equal to one right angle.
Which of the following options is correct?
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Answer
A tangent line touches the circle at one point. A radius connects the center to the circumference.
The angle between a radius and tangent at the point of contact is always 90°. This is a fundamental property of circles.
So, statement 2 is true.
But, statement 1 is false as not all radius forms angle of 90° with all the tangents.
∴ Statement 1 is false, and statement 2 is true.
Hence, option 4 is the correct option.
Assertion (A) : The radius of a circle is 20 cm, then the length of its largest chord is also 20 cm.
Reason (R) : Longest chord of a circle is equal to its diameter.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
As we know that radius is half of the diameter.
Diameter = 2 x radius = 2 x 20 = 40 cm.
We know that,
Longest chord of a circle is equal to its diameter.
So, reason (R) is true.
Longest chord = 40 cm
So, assertion (A) is false.
∴ A is false, but R is true.
Hence, option 4 is the correct option.
Assertion (A) : When the radius of a circle is increased by 3 cm, its diameter will increase by 2 x 3 cm.
Reason (R) : Original radius is r cm, original diameter 2r cm
∴ Increase in length of diameter = 2(r + 3) cm - 2r
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
Original radius = r cm
Original diameter = 2r cm
New radius = (r + 3) cm
New diameter = 2(r + 3) cm
Increase in length of diameter = New diameter - Original diameter
= 2(r + 3) - 2r
= 2r + 2 x 3 - 2r
= 2 x 3
= 6 cm.
∴ Both A and R are correct, and R is the correct explanation for A.
Hence, option 1 is the correct option.
Assertion (A) : If a circle is of radius 8 cm and the length of its minor arc is also 8 cm, then the length of major arc = 8(2π - 1) cm.
Reason (R) : For every circle, sum of the length of its major arc and length of its minor arc is equal to the circumference of the circle.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
Given, radius of a circle = 8 cm and the length of its minor arc = 8 cm
Circumference of the circle = 2πr = 2 x π x 8 = 16π
We know that,
Length of minor arc + length of major arc = Circumference of the circle
So, reason (R) is true.
⇒ 8 + length of major arc = 16π
⇒ length of major arc = 16π - 8
⇒ length of major arc = 8(2π - 1) cm
So, assertion (A) is true.
∴ Both A and R are correct, and R is the correct explanation for A.
Hence, option 1 is the correct option.
Assertion (A) : A, B and C are three points on the circumference of a circle such that BC is diameter of the circle. If AC = 4 cm and AB = 3 cm, then diameter BC = 4 cm + 3 cm.
Reason (R) : Angle BAC = angle of semi-circle = 90° and so BC2 = AB2 + AC2
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
Given, AC = 4 cm and AB = 3 cm
Since BC is the diameter, angle BAC is a right angle.
Triangle ABC is a right triangle with hypotenuse BC.
Using Pythagoras theorem,
BC2 = AB2 + AC2
So, reason (R) is true.
⇒ BC2 = 32 + 42
⇒ BC2 = 9 + 16
⇒ BC2 = 25
⇒ BC =
⇒ BC = 5 cm.
So, assertion (A) is false.
∴ A is false, but R is true.
Hence, option 4 is the correct option.
The following figure shows the circle with centre O.
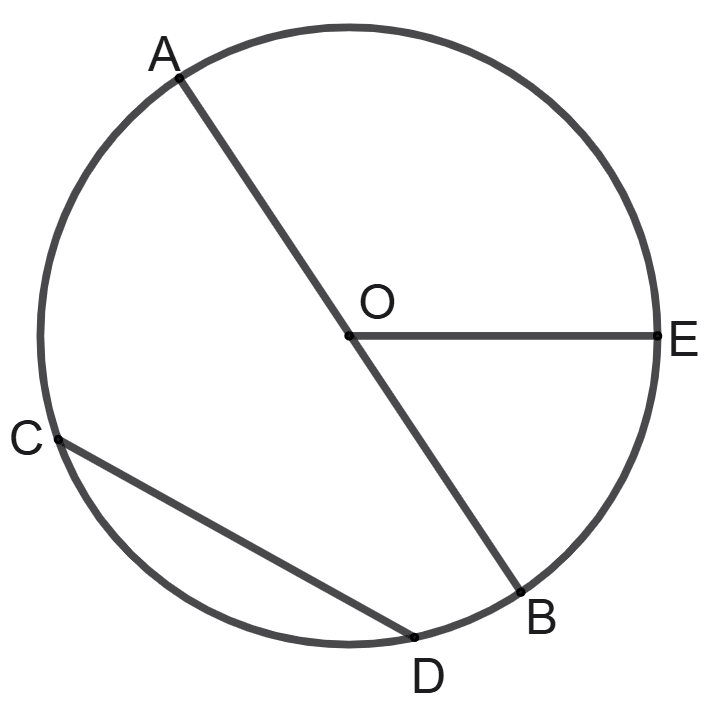
Use the figure to fill the blanks in each of the following :
(i) AB = .................
(ii) Radius = ................
(iii) Chords = ........... and ...........
(iv) Diameter = ............
(v) AB = 2 x .............
Answer
(i) AB = Diameter
(ii) Radius = OE = OA = OB
(iii) Chords = CD and AB
(iv) Diameter = AB
(v) AB = 2 x OE = OA = OB
M is a fixed point in a plane and a point P moves in the same plane such that PM = 10 cm. State :
(i) the name of the figure formed.
(ii) the length of the radius of the circle.
(iii) the length of the diameter of the circle.
Can a chord of length 16 cm can be drawn in this circle? Give reason.
Answer
(i) Given, M is a fixed point. P moves such that PM = 10 cm.
A circle is a set of points equidistant from a center or a fixed point.
Hence, the figure is circle with M as center.
(ii) M is the center of the circle and PM is the radius of the circle.
Hence, the length of the radius of the circle = 10 cm.
(iii) As we know that the diameter is twice the radius.
Diameter = 2 x 10 cm = 20 cm
Hence, the length of the diameter of the circle = 20 cm.
The longest chord is the diameter.
The diameter is 20 cm.
A chord of length 16 cm can be drawn since 16 < 20.
Hence, a chord of length 16 cm can be drawn in this circle.
The radius of a circle is 6 cm. Find its diameter. If O is the centre of the circle; state, giving reasons, the position of points A, B and C; if;
(i) OA = 4.8 cm
(ii) OB = 7.5 cm
(iii) OC = 6 cm
Answer
The radius of a circle = 6 cm
As, the diameter is twice the radius.
Diameter = 2 x 6 cm = 12 cm.
(i) OA = 4.8 cm
As, 4.8 < 6 (Radius)
Hence, A lies inside the circle.
(ii) OB = 7.5 cm
As, 7.5 > 6 (Radius)
Hence, B lies outside the circle.
(iii) OC = 6 cm
As, 6 = 6 (Radius)
Hence, C lies on the circumference of the circle.
Fill in the blanks :
(i) An arc is the part of the ...................
(ii) Diameter of a circle bisects ............
(iii) The part of the circumference greater than the semicircle is called ................
(iv) Sector of a circle is its region bounded by .................
(v) The segment of a circle is the region bounded by ..................
(vi) A tangent of a circle meets the circle at ..............
(vii) The number of tangents that can be drawn through a point on its circumference = ...............
(viii) The number of tangent that can be drawn through a point outside the circle is .................
Answer
(i) An arc is a part of the circumference of the circle.
(ii) Diameter of a circle bisects circumference of the circle.
(iii) The part of the circumference greater than the semicircle is called major-arc.
(iv) Sector of a circle is its region bounded by two radii and an arc.
(v) The segment of a circle is the region bounded by a chord and an arc.
(vi) A tangent of a circle meets the circle at one point only.
(vii) The number of tangents that can be drawn through a point on its circumference = only one.
(viii) The number of tangent that can be drawn through a point outside the circle is two.
O is the center of a circle with diameter 30 cm. P is a point outside the circle and PA is tangent of the circle. Find :
(i) the length of tangent PA; if OP = 39 cm.
(ii) the distance between O and P, if the length of the tangent PA is 20 cm.
Answer
Given, diameter = 30 cm
As we know that the diameter is twice the radius.
⇒ Radius = = 15 cm.

(i) It is given that OP = 39 cm.
In ∆ OPA,
∠OAP = 90°.
By pythagoras theorem,
⇒ OA2 + PA2 = OP2
⇒ 152 + PA2 = 392
⇒ 225 + PA2 = 1521
⇒ PA2 = 1521 - 225
⇒ PA2 = 1296
⇒ PA =
⇒ PA = 36 cm.
Hence, the length of tangent PA = 36 cm.
(ii) Given,
PA = 20 cm
⇒ OA2 + PA2 = OP2
⇒ 152 + 202 = OP2
⇒ 225 + 400 = OP2
⇒ OP2 = 625
⇒ OP =
⇒ OP = 25 cm.
Hence, the distance between O and P = 25 cm.
The following figure shows a circle with center O and a diameter AB.

(i) Name the angle APB.
(ii) State the measure of angle APB.
(iii) If AP = 12 cm and OA = 10 cm; find the lengths of AB and BP.
(iv) If 4AP = 3PB = 12 cm; find the radius of the circle.
Answer
(i) AB is diameter of the circle.
Hence, angle APB is the angle of semi-circle.
(ii) As, the angle subtended by a diameter at any point on the circumference of a circle is a right angle (90°).
Hence, angle APB = 90°.
(iii) Given,
AP = 12 cm and OA = 10 cm
⇒ OA = OB (Radii of the circle)
⇒ OB = 10 cm
From figure,
⇒ AB = OA + OB = 10 cm + 10 cm = 20 cm
Since, angle APB = 90°.
Using pythagoras theorem,
⇒ AP2 + PB2 = AB2
⇒ 122 + PB2 = 202
⇒ 144 + PB2 = 400
⇒ PB2 = 400 - 144
⇒ PB2 = 256
⇒ PB =
⇒ PB = 16 cm.
Hence, AB = 20 cm and PB = 16 cm.
(iv) Given,
⇒ 4AP = 3PB = 12 cm
⇒ AP = = 3 cm
⇒ PB = = 4 cm
Since, angle APB = 90°.
Using pythagoras theorem,
⇒ AP2 + PB2 = AB2
⇒ 32 + 42 = AB2
⇒ 9 + 16 = AB2
⇒ 25 = AB2
⇒ AB =
⇒ AB = 5 cm
Now, OA = OB (Radii of the circle)
From figure,
⇒ AB = OA + OB
⇒ AB = 2 x OA
⇒ 5 = 2 x OA
⇒ OA = = 2.5 cm.
Hence, the radius of the circle = 2.5 cm.
Find the length of the tangent to a circle with radius 5 cm, from a point at a distance of 13 cm from its center.
Answer
Consider a circle with center O. Let AP is the tangent of the circle.
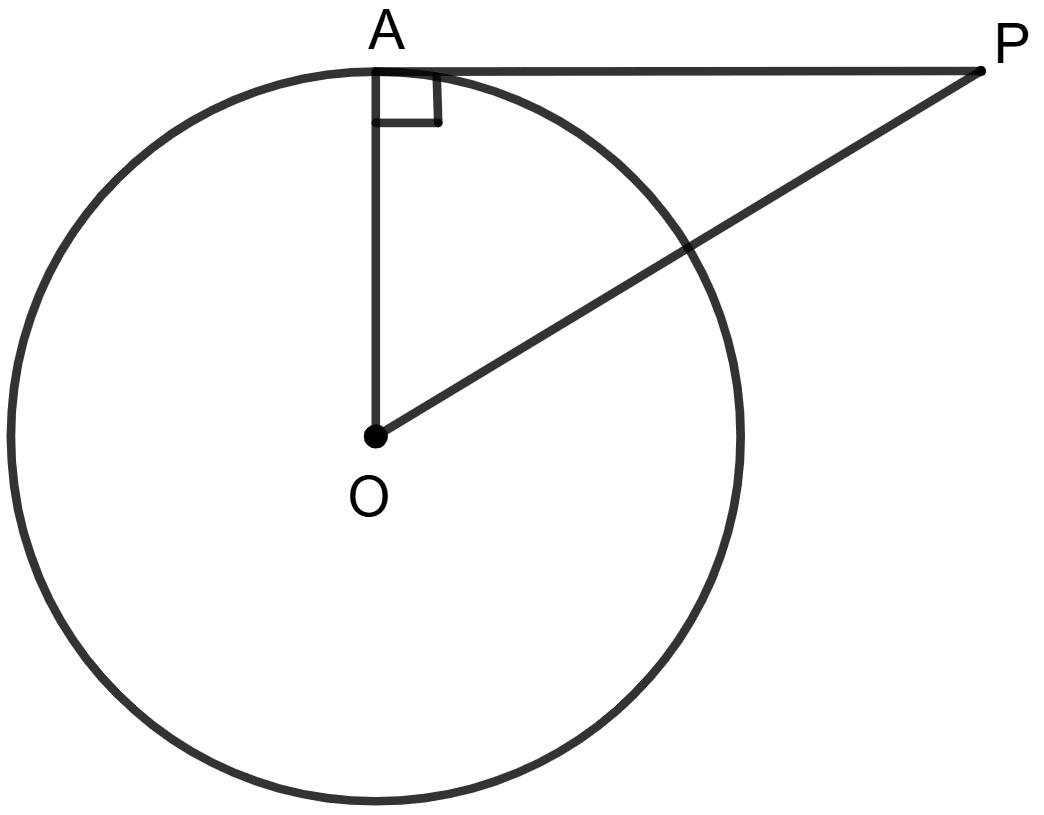
We know that,
Tangent and radius to the circle at point of contact are perpendicular to each other.
In the ∆OPA,
∠OAP = 90°.
By pythagoras theorem,
⇒ OA2 + PA2 = OP2
⇒ 52 + PA2 = 132
⇒ 25 + PA2 = 169
⇒ PA2 = 169 - 25
⇒ PA2 = 144
⇒ PA =
⇒ PA = 12 cm
Hence, the length of the tangent = 12 cm.
The following figure shows a circle with diameter AB and center at point O.
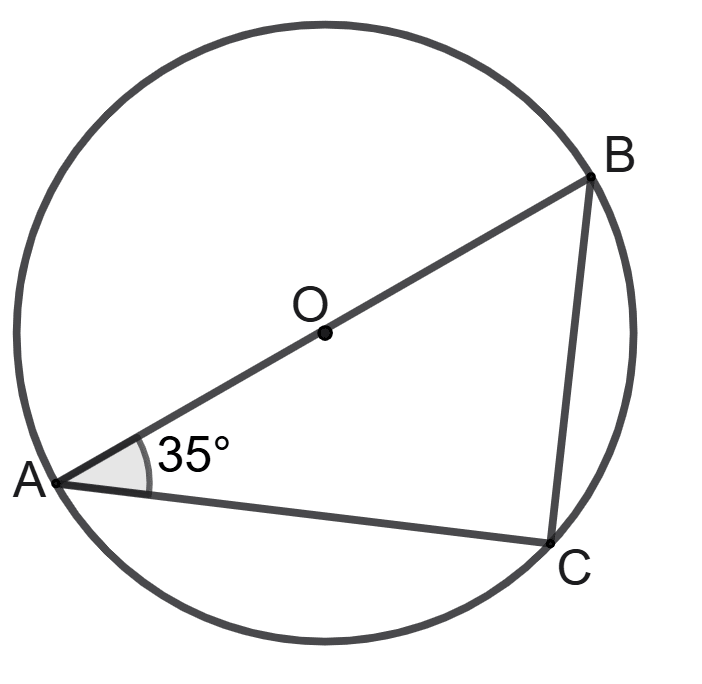
If angle CAB = 35°, find the measure of angle ABC.
Answer
We know that,
Angle in a semi-circle is a right angle.
So, angle ACB = 90°.
In ∆ ACB,
Using angle sum property,
⇒ ∠ABC + ∠ACB + ∠CAB = 180°
⇒ ∠ABC + 90° + 35° = 180°
⇒ ∠ABC + 125° = 180°
⇒ ∠ABC = 180° - 125°
⇒ ∠ABC = 55°.
Hence, angle ABC = 55°.
Draw a circle with radius 3 cm and centre at point O. Draw two radii OA and OB of the circle drawn such that ∠AOB = 60°. Join A and B and measure the length of AB.
Answer
Steps of construction :
Mark a point O.
With O as center and radius equal to 3 cm draw a circle.
Draw OA as the radius of the circle.
Draw another radius OB at an angle of 60° with OA.
Join A and B. Measure AB.
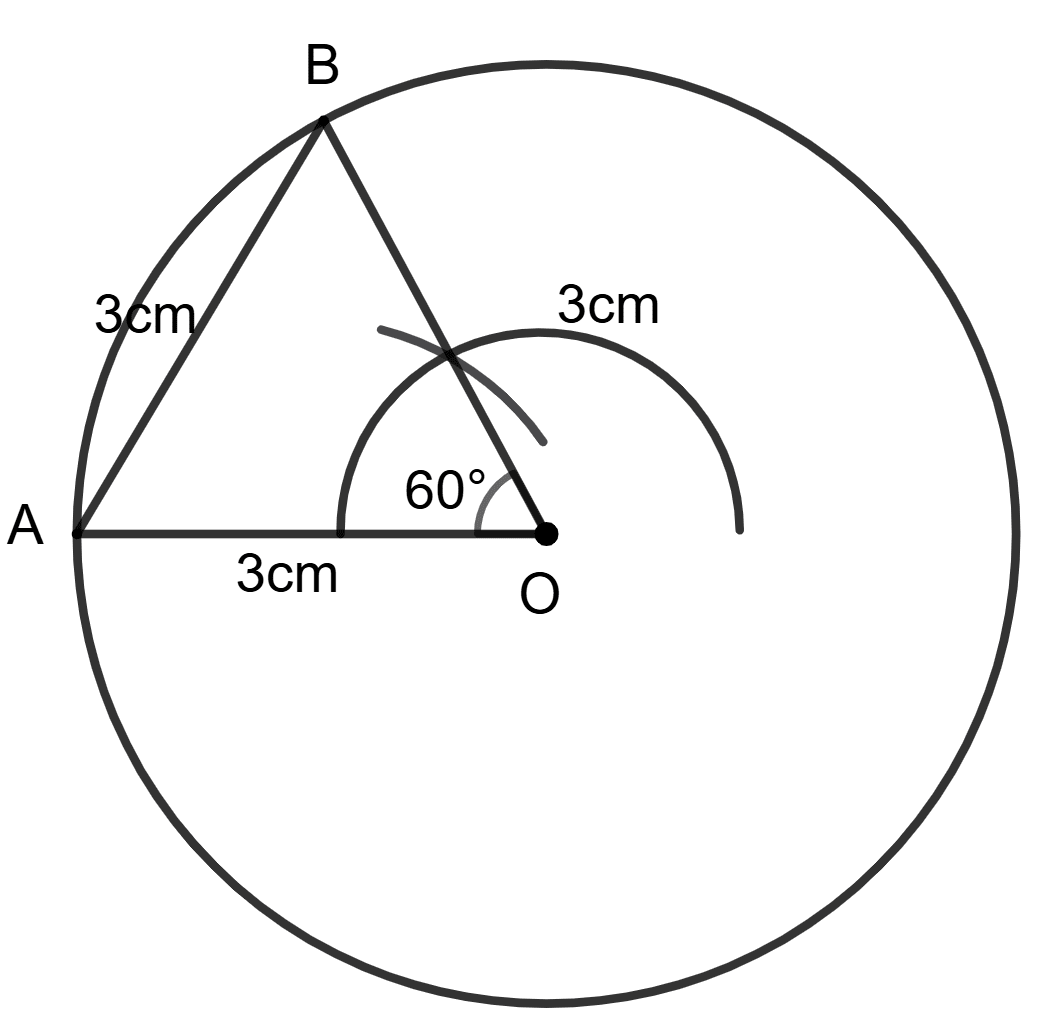
Hence, the length of AB = 3 cm.
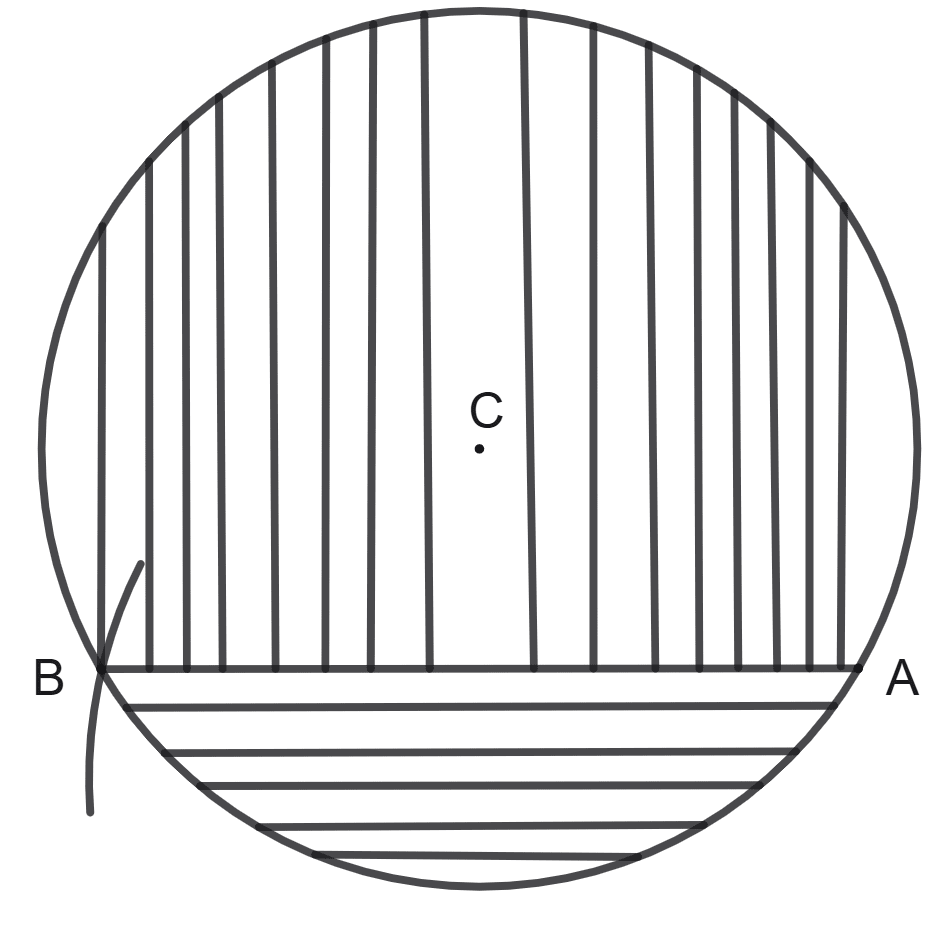
Draw a circle with radius 4 cm. Draw a chord AB of length 6 cm. Shade its minor segment by horizontal lines and major segment by vertical lines.
Answer
Steps of construction:
Draw a circle of radius 4 cm and mark the centre as C.
Mark a point A on the circle.
Draw an arc with A as centre and radius 6 cm to cut the circle at B.
Join the line AB.
Shade the segment which contains the centre 'C' by vertical lines.
Shade the segment which does not contain the centre 'C' by horizontal lines.
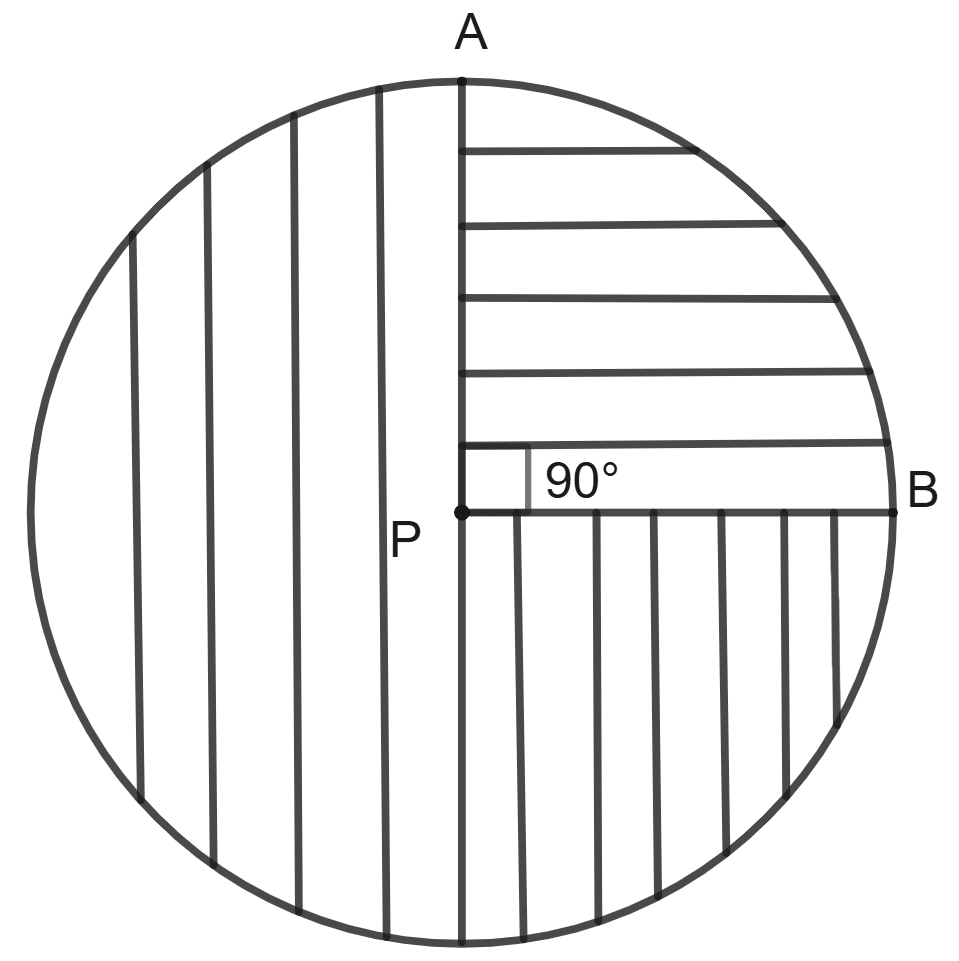
Draw a circle with centre at point P. Draw its radii PA and PB such that angle APB = 90°. Shade the minor sector of the circle by horizontal lines and its major sector by vertical lines.
Answer
Steps of construction:
Draw a circle of any radius and mark the centre as P.
Draw a straight line PB.
Draw an angle APB such that angle APB = 90°, where A is a point on the circumference of the circle.
Shade the major segment by vertical lines.
Shade the minor segment by horizontal lines.
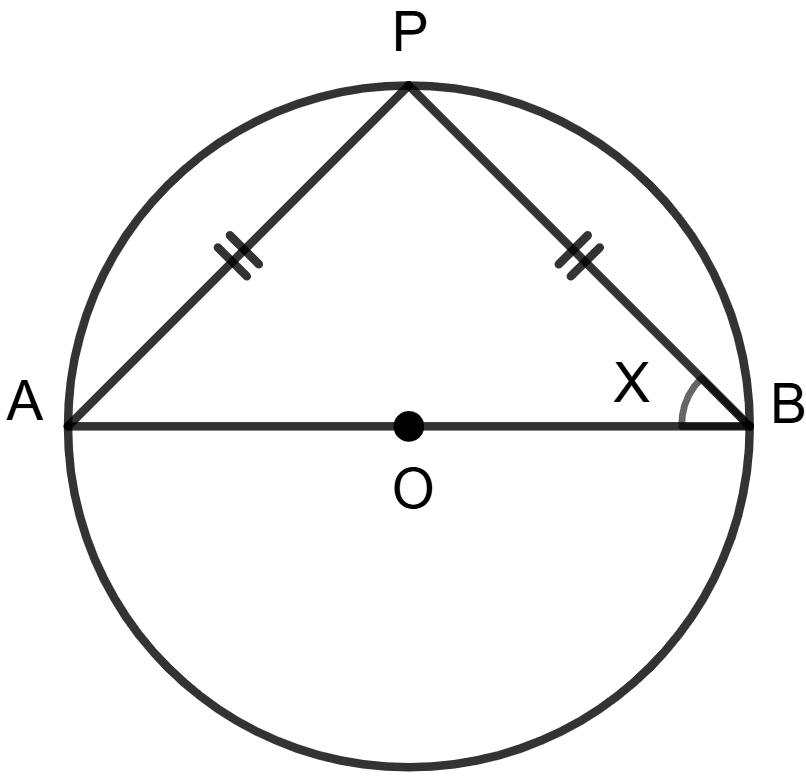
In a circle with centre O and diameter AB; angle APB is the angle of semicircle. If PA = PB; find the measure of each angle of triangle APB.
Answer
Given, O is center of circle. AB is the diameter of the circle.
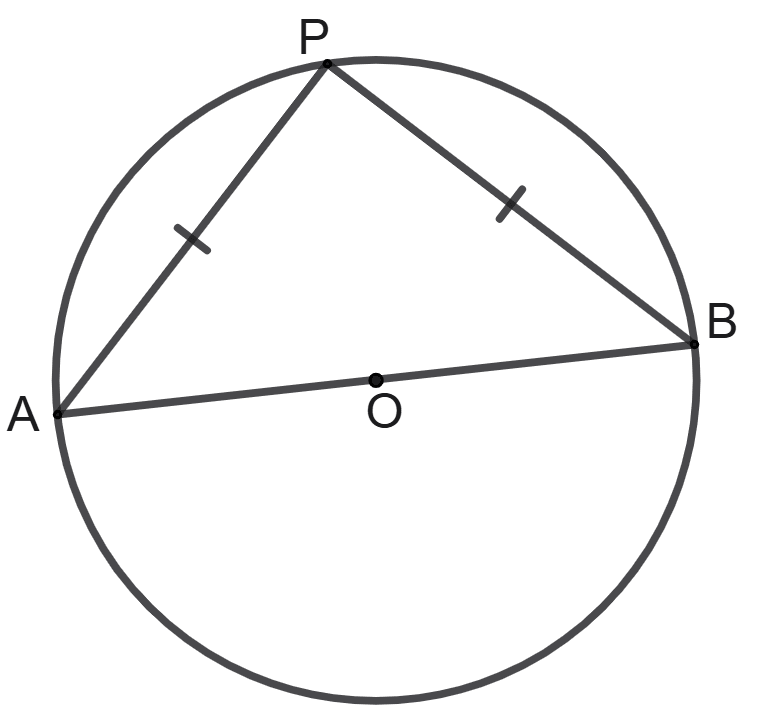
⇒ PA = PB (Given)
⇒ ∠PAB = ∠PBA = x (let) [Angles opposite to equal sides of a triangle are always equal]
We know that,
Angle in a semi-circle is a right angle.
⇒ ∠APB = 90°
In ΔAPB, using angle sum property
⇒ ∠PAB + ∠PBA + ∠APB = 180°
⇒ x + x + 90° = 180°
⇒ 2x = 180° - 90°
⇒ 2x = 90°
⇒ x =
⇒ x = 45°
⇒ ∠PAB = ∠PBA = 45°
Hence, all angles of the triangles are 45°, 45° and 90°.
In the following figure, O is the centre of the circle and AB is a diameter.
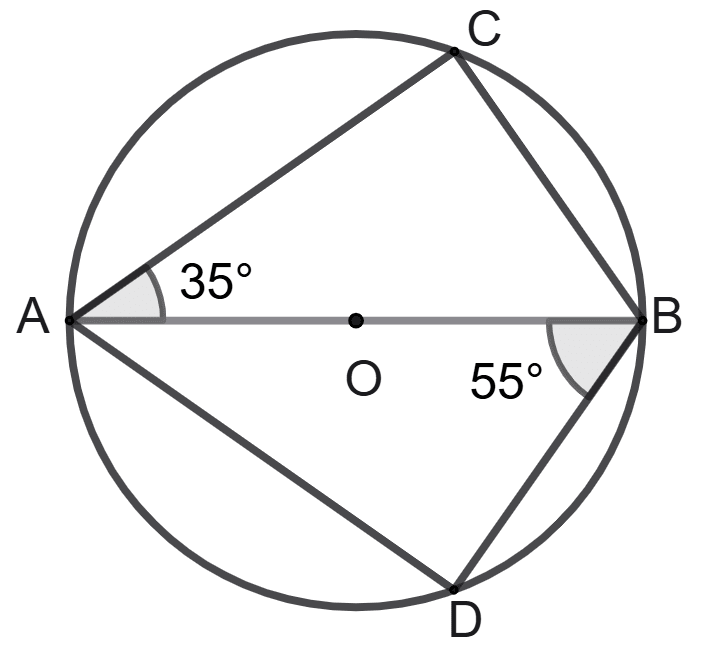
C and D are the points on the circumference of the circle such that ∠CAB = 35° and ∠ABD = 55°. Find the measures of angles CAD and CBD.
Answer
We know that,
Angle in a semi-circle is a right angle.
⇒ ∠ACB = ∠ADB = 90°
In ΔACB, using angle sum property
⇒ ∠CAB + ∠CBA + ∠ACB = 180°
⇒ 35° + ∠CBA + 90° = 180°
⇒ 125° + ∠CBA = 180°
⇒ ∠CBA = 180° - 125°
⇒ ∠CBA = 55°
From figure,
⇒ ∠CBD = ∠CBA + ∠ABD = 55° + 55° = 110°.
Similarly, in ΔADB, using angle sum property
⇒ ∠DAB + ∠DBA + ∠ADB = 180°
⇒ ∠DAB + 55° + 90° = 180°
⇒ ∠DAB + 145° = 180°
⇒ ∠DAB = 180° - 145°
⇒ ∠DAB = 35°
From figure,
⇒ ∠CAD = ∠CAB + ∠DAB = 35° + 35° = 70°.
Hence, angles CAD = 70° and angle CBD = 110°.
The following figure shows a circle with centre O and diameter PQ. Point R lies on the circumference of the circle such that PR = QR and PR = 4 cm.
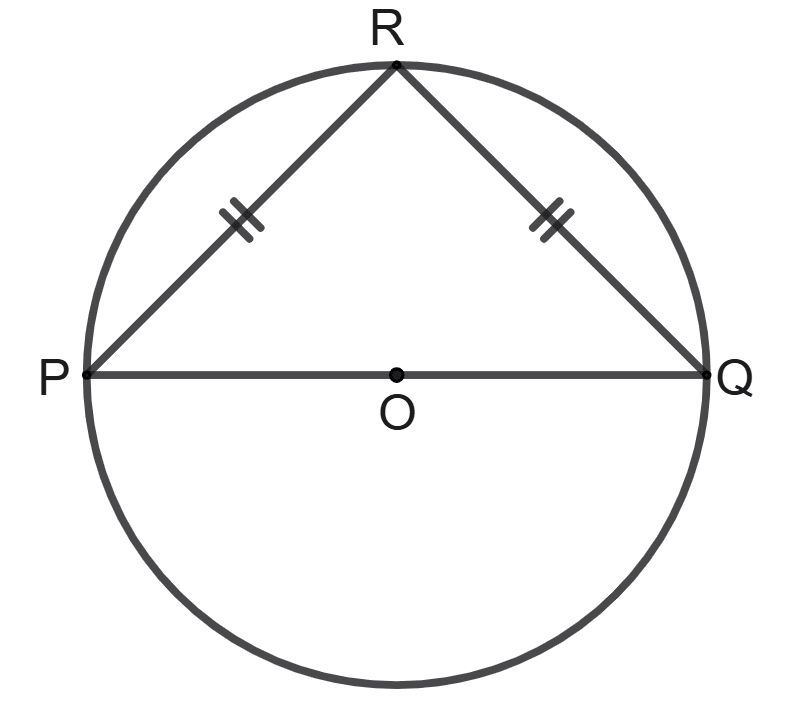
Calculate the radius of the given circle and state its value correct to two decimal places.
Answer
Given, PQ is diameter of the circle.
PR = QR and PR = 4 cm
⇒ QR = 4 cm
As we know that,
Angle in a semi-circe is a right angle.
⇒ ∠PRQ = 90°
Triangle PQR is a right triangle with hypotenuse PQ. Using Pythagoras theorem,
⇒ PQ2 = PR2 + RQ2
⇒ PQ2 = 42 + 42
⇒ PQ2 = 16 + 16
⇒ PQ2 = 32
⇒ PQ = = 5.66 cm
Radius (OP) =
= 2.83 cm.
Hence, the radius of the given circle = 2.83 cm.
In the following figure, PQ and PR are the tangent to the circle with centre O. Line segment AC touch the circle at point B.
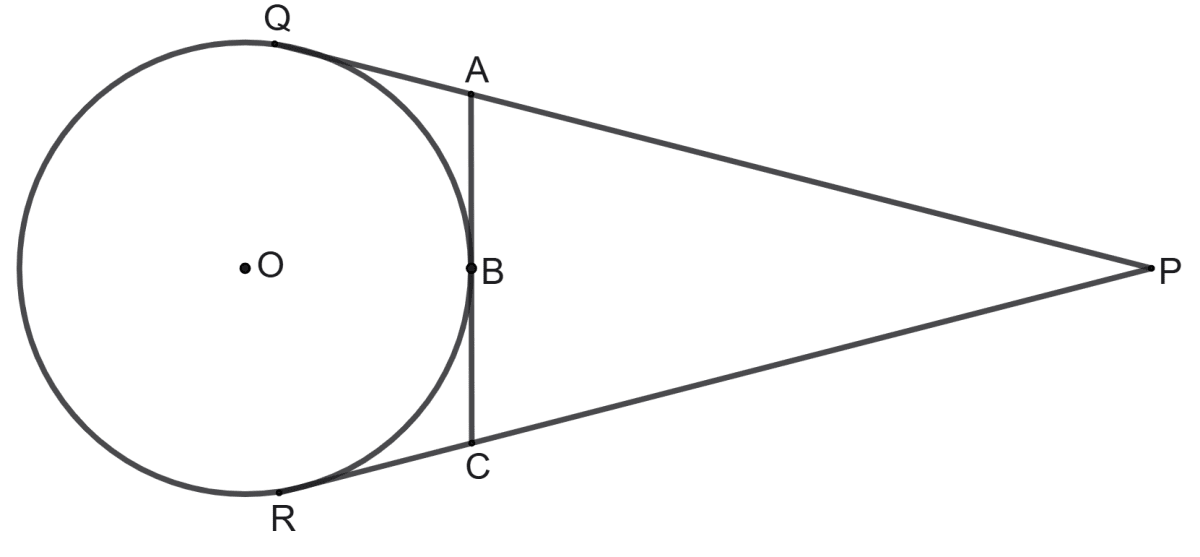
(i) State the relation between tangent PQ and PR.
Also show that:
(ii) PQ = PA + AB
(iii) PR = PC + CB
(iv) PQ + PR = Perimeter of ΔPAC.
Answer
(i) PQ and PR are the tangent to the circle with centre O.
As we know that,
Through any point, outside a circle at most two tangent can be drawn and both of these tangent are always equal to each other.
Here, point P lies outside the circle and the two tangent PQ and PR are drawn to the circle.
Hence, PQ = PR.
(ii) When point A lies outside the circle and the two tangent AQ and AB are drawn to the circle. Then,
AQ = AB ....................(1)
From figure,
⇒ PQ = PA + AQ
From equation (1),
⇒ PQ = PA + AB
Hence, proved that PQ = PA + AB.
(iii) When point C lies outside the circle and the two tangent CR and CB are drawn to the circle. Then
CR = CB ....................(2)
From figure,
⇒ PR = PC + CR
From equation (2),
⇒ PR = PC + CB
Hence, proved that PR = PC + CB.
(iv) Perimeter of triangle PAC = PA + PC + AC
= PA + PC + (AB + CB)
= PA + PC + (AQ + CR)
= (PA + AQ) + (PC + CR)
= PQ + PR
Hence, proved that PQ + PR = Perimeter of Δ PAC.
From an external point P, the tangent PA is drawn to the circle with centre O.
(i) If OP = 20 cm and tangent PA = 16 cm find the diameter of the circle.
(ii) If diameter of the circle is 20 cm and tangent PA = 24 cm, find the length of OP.
Answer
O is center of the circle. PA is the tangent of the circle.
We know that,
Tangent and radius through the center at point of contact are perpendicular to each other.
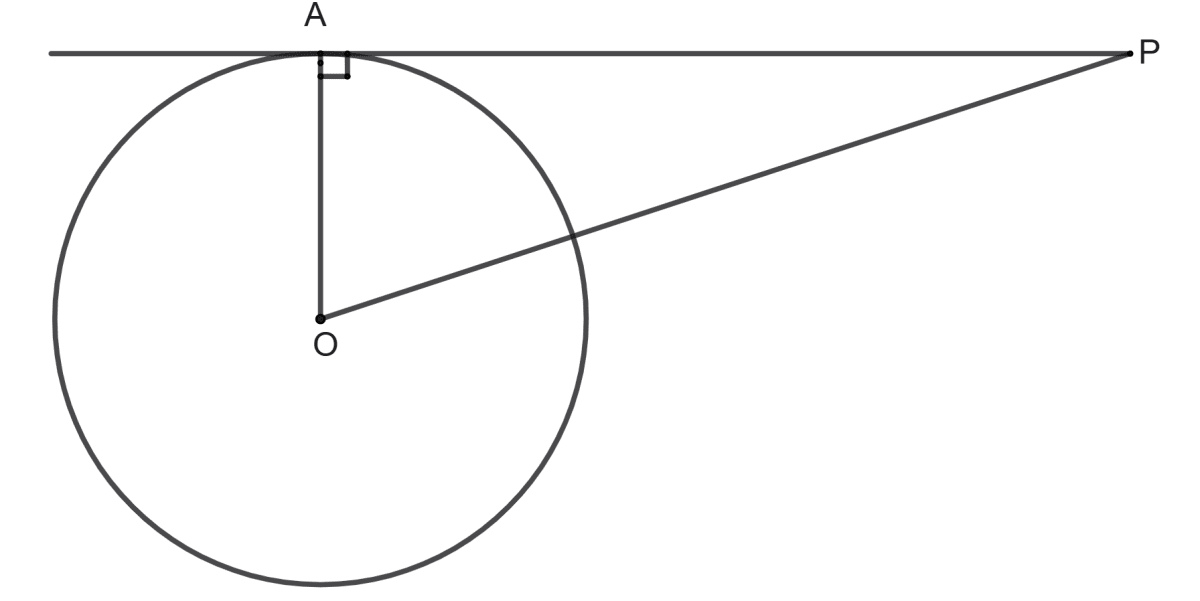
(i) Given, OP = 20 cm and PA = 16 cm
In the ∆OPA as we know that ∠OAP = 90°.
As we know Pythagoras theorem can be used in a right angled triangle,
⇒ OA2 + PA2 = OP2
⇒ OA2 + 162 = 202
⇒ OA2 + 256 = 400
⇒ OA2 = 400 - 256
⇒ OA2 = 144
⇒ OA =
⇒ OA = 12 cm
By formula,
Diameter = 2 x radius = 2 x 12 = 24 cm.
Hence, the diameter of the circle = 24 cm.
(ii) Given, diameter = 20 cm and PA = 24 cm
Radius (OA) = = 10 cm
In the ∆ OPA as we know that ∠OAP = 90°.
As we know Pythagoras theorem can be used in a right angled triangle,
⇒ OA2 + PA2 = OP2
⇒ 102 + 242 = OP2
⇒ 100 + 576 = OP2
⇒ OP2 = 676
⇒ OP =
⇒ OP = 26 cm.
Hence, the length of OP = 26 cm.
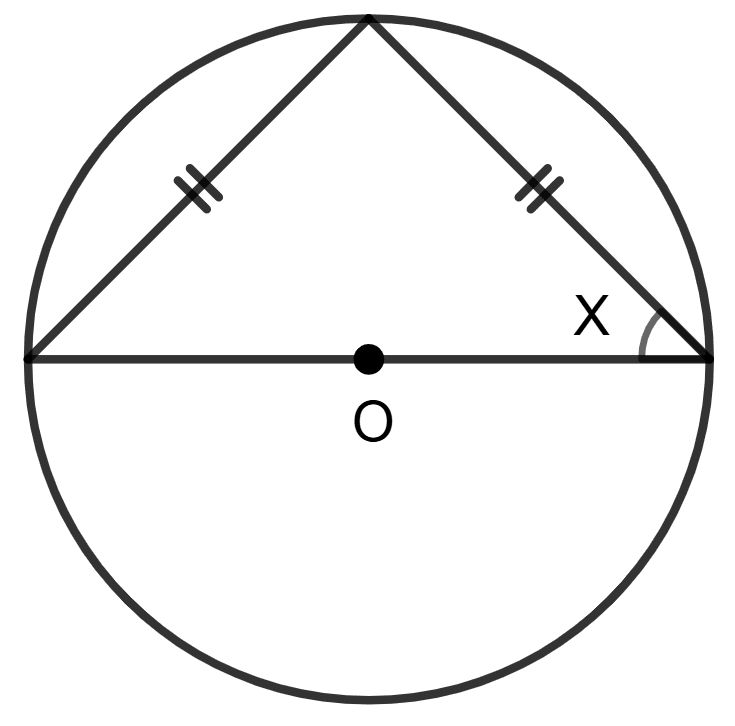
In figure given below, O is the centre of the circle, use the given information to find the value of x:
Answer
PA = PB (Given)
⇒ ∠PAB = ∠PBA = x (let) [Angles opposite to equal sides of a triangle are always equal]
As we know that the angle subtended by a diameter at any point on the circumference of a circle is a right angle (90°).
⇒ ∠APB = 90°
In ΔAPB, using angle sum property
⇒ ∠PAB + ∠PBA + ∠APB = 180°
⇒ x + x + 90° = 180°
⇒ 2x = 180° - 90°
⇒ 2x = 90°
⇒ x =
⇒ x = 45°
⇒ ∠PAB = ∠PBA = 45°
Hence, the value of x = 45°.
In figure given below, O is the centre of the circle, use the given information to find the value of x:
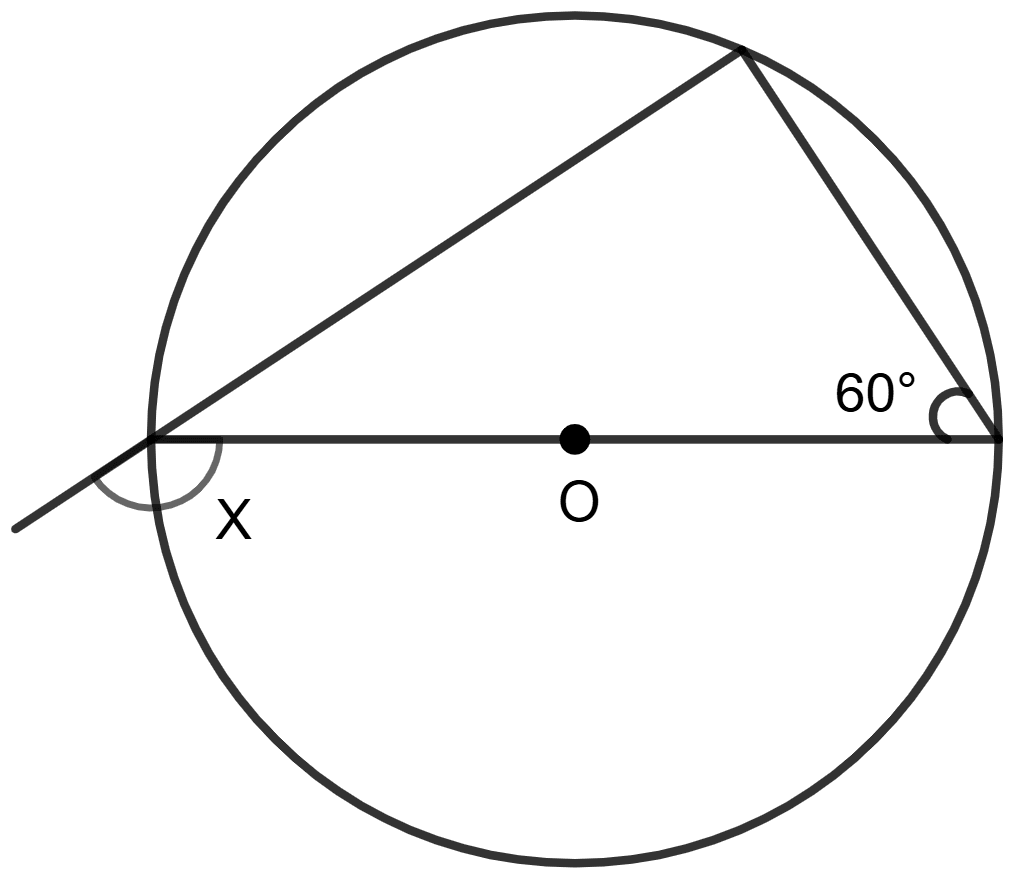
Answer
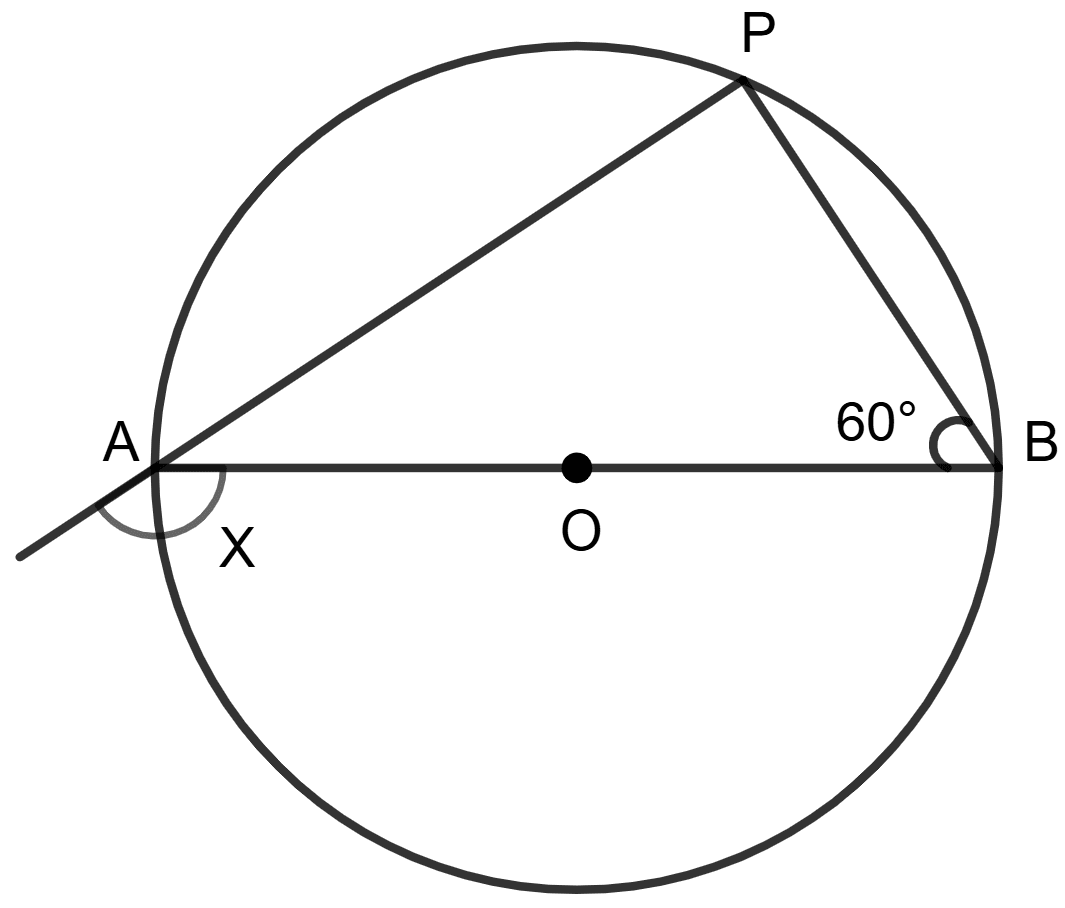
As we know that the angle subtended by a diameter at any point on the circumference of a circle is a right angle (90°).
⇒ ∠APB = 90°
According to exterior angle theorem,
Exterior angle of a triangle is equal to the sum of the two opposite interior angles.
⇒ ex. ∠A = ∠APB + ∠ABP
⇒ x = 90° + 60° = 150°
Hence, the value of x = 150°.
In figure given below, O is the centre of the circle, use the given information to find the value of x:
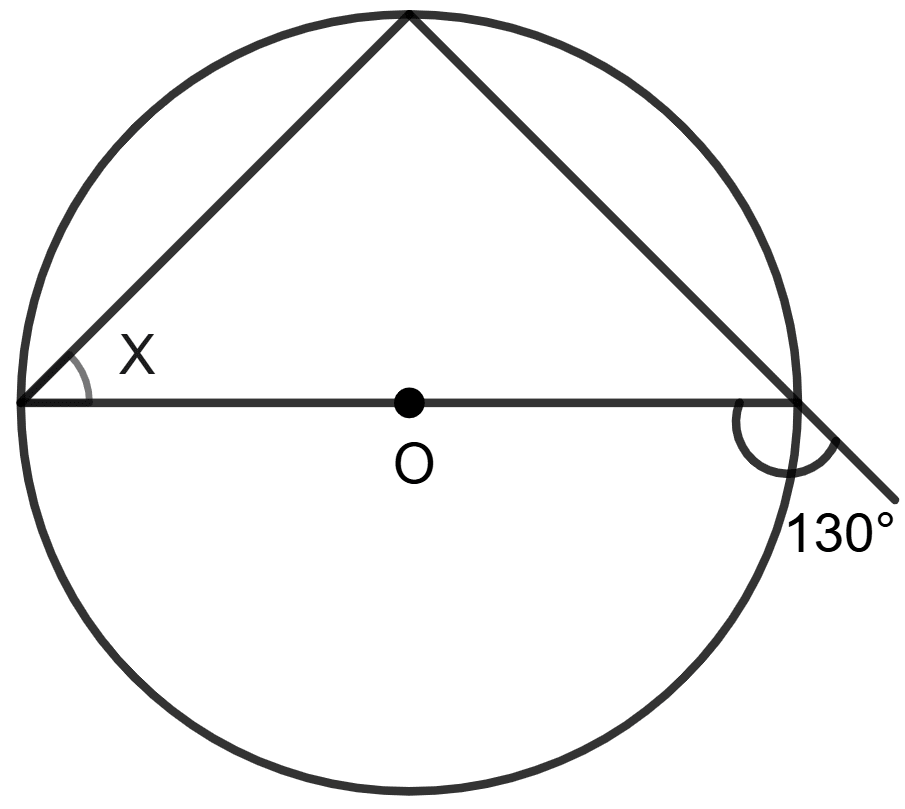
Answer
As we know that the angle subtended by a diameter at any point on the circumference of a circle is a right angle (90°).
⇒ ∠APB = 90°
According to exterior angle theorem,
Exterior angle of a triangle is equal to the sum of the two opposite interior angles.
⇒ ex. ∠A = ∠APB + ∠ABP
⇒ 130° = 90° + x
⇒ x = 130° - 90°
⇒ x = 40°.
Hence, the value of x = 40°.
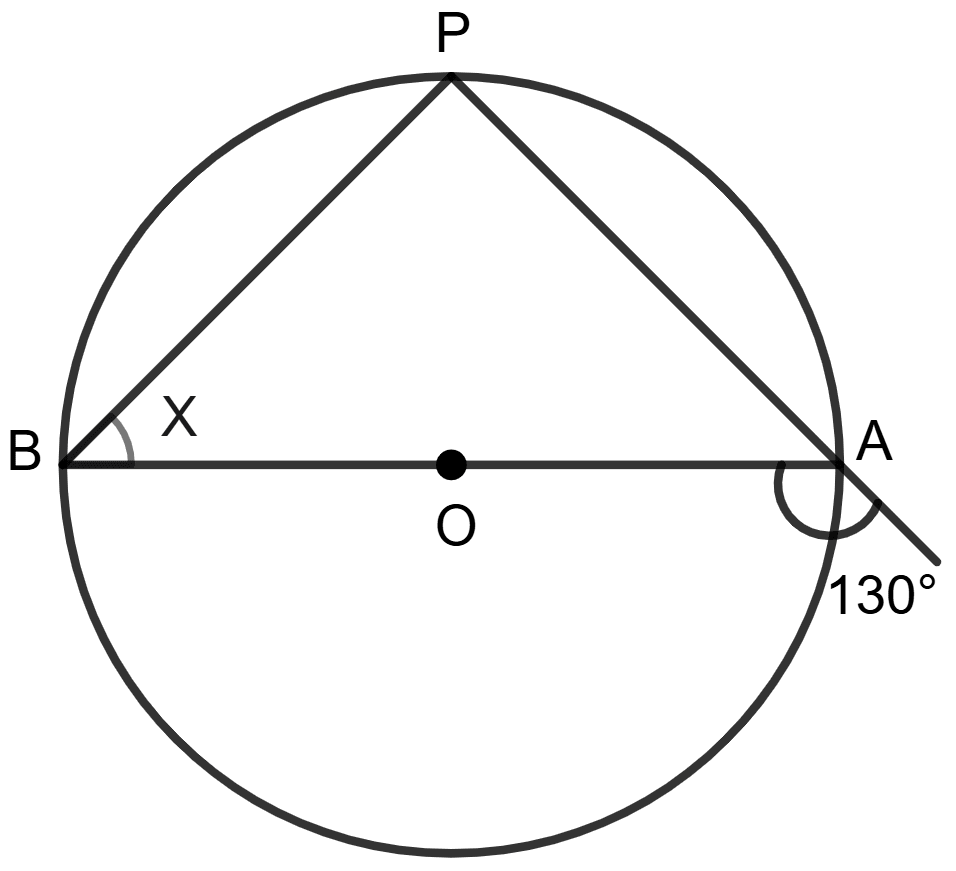
In figure given below, O is the centre of the circle, use the given information to find the value of x:
Answer
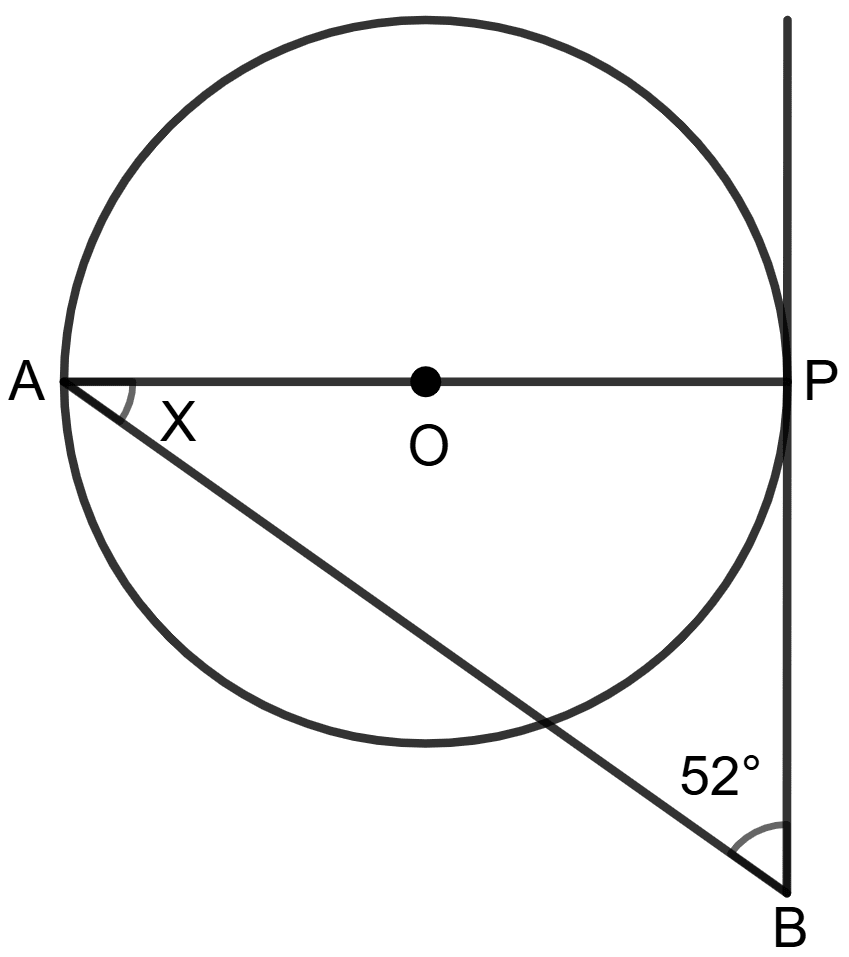
At the point of contact, the angle between tangent and the radius is always 90°.
⇒ ∠APB = 90°
In ΔAPB, using angle sum property
⇒ ∠PAB + ∠PBA + ∠APB = 180°
⇒ x + 52° + 90° = 180°
⇒ x + 142° = 180°
⇒ x = 180° - 142°
⇒ x = 38°.
Hence, the value of x = 38°.
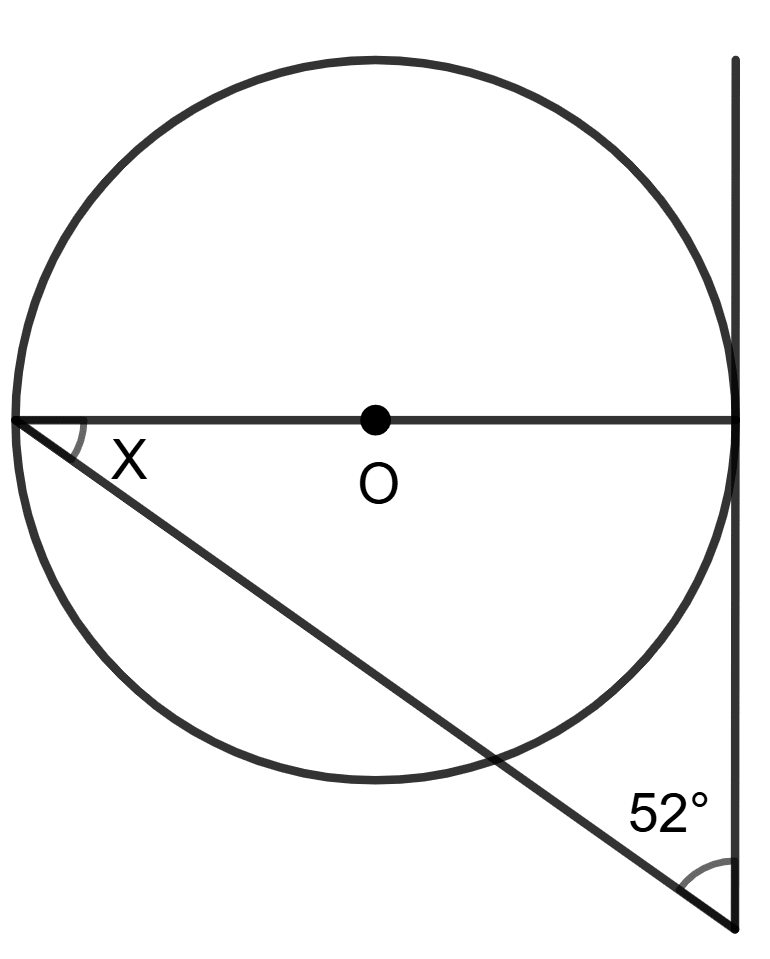
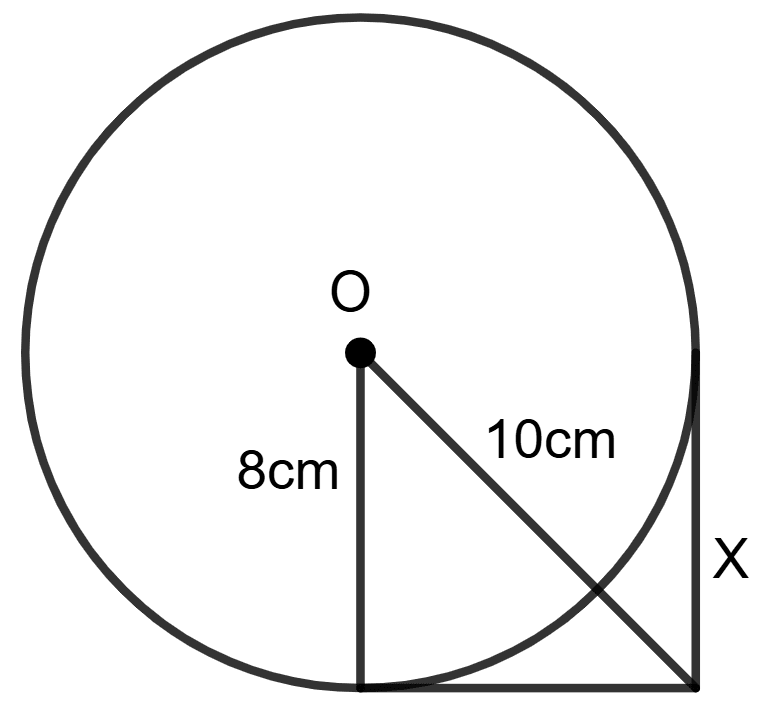
In figure given below, O is the centre of the circle, use the given information to find the value of x:
Answer
At the point of contact, the angle between tangent and the radius is always 90°.
⇒ ∠OAB = 90°
Triangle OAB is a right triangle with hypotenuse OB. Using Pythagoras theorem,
⇒ OB2 = OA2 + AB2
⇒ 102 = 82 + AB2
⇒ 100 = 64 + AB2
⇒ AB2 = 100 - 64
⇒ AB2 = 36
⇒ AB =
⇒ AB = 6 cm
We know that,
Tangents from an exterior point to a circle are equal in length.
⇒ BC = BA
⇒ x = 6 cm.
Hence, the value of x = 6 cm.
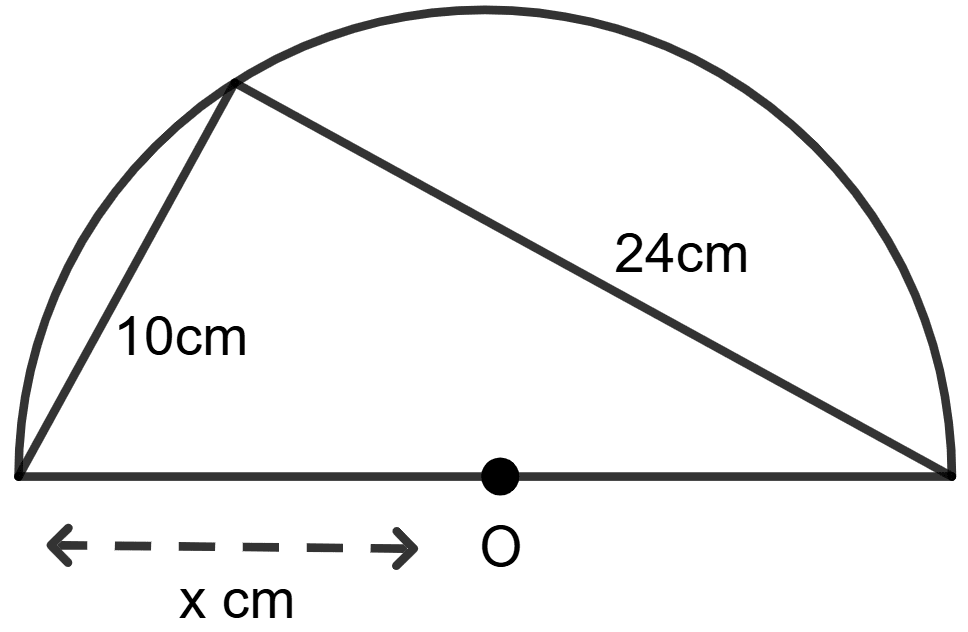
In figure given below, O is the centre of the circle, use the given information to find the value of x:
Answer
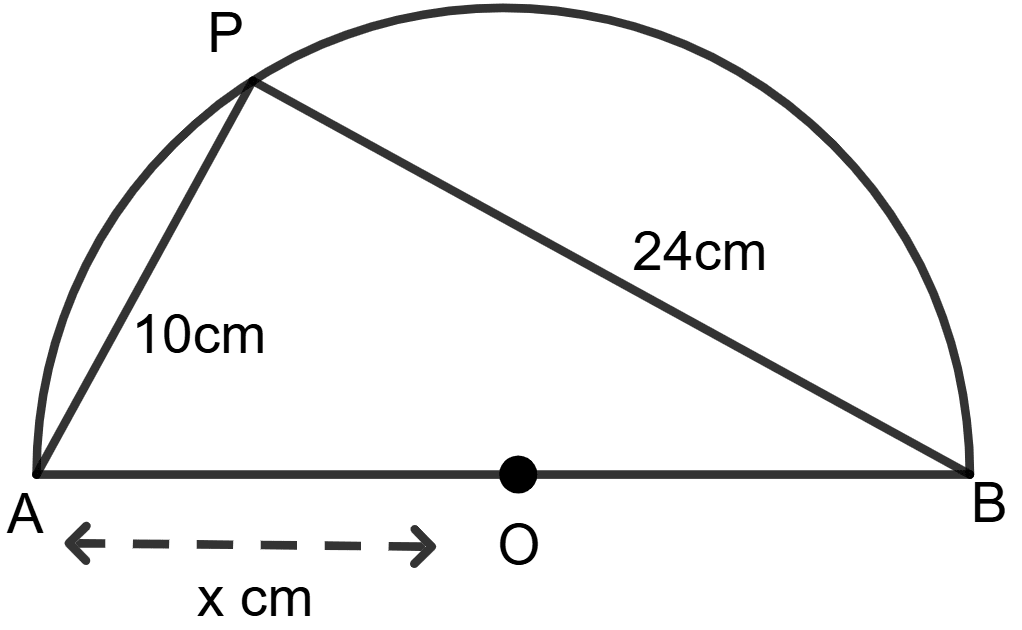
Angle in semi-circle is a right angle.
⇒ ∠APB = 90°
Triangle APB is a right triangle with hypotenuse AB. Using Pythagoras theorem,
⇒ AB2 = PA2 + PB2
⇒ AB2 = 102 + 242
⇒ AB2 = 100 + 576
⇒ AB2 = 676
⇒ AB =
⇒ AB = 26 cm
Radius is half of the diameter.
⇒ x =
⇒ x = = 13 cm.
Hence, the value of x = 13 cm.