The value of x + y + z + r is:
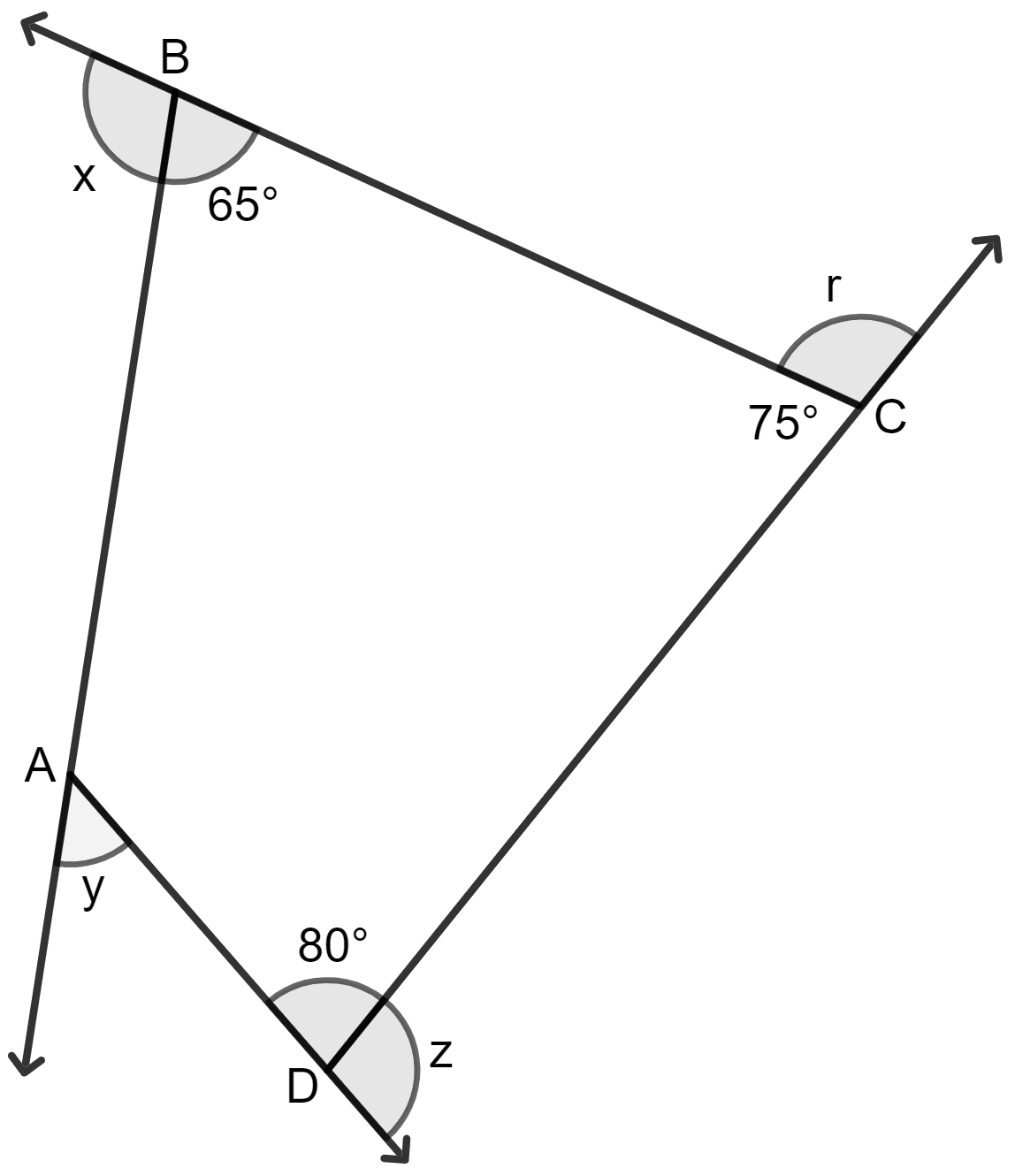
180°
270°
360°
720°
Answer
According to the properties of a polygon, the sum of all exterior angles is always 360°.
This is clearly shown in the figure, where x, y, z, and r represent the exterior angles of the polygon.
Thus, x + y + z + r = 360°.
Hence, option 3 is the correct option.
The angles of a quadrilateral are in the ratio in the ratio 2 : 5 : 7 : 4. The largest angle is:
40°
100°
140°
80°
Answer
As we know, the sum of all the angles in a quadrilateral is 360°.
The angles are in the ratio 2 : 5 : 7 : 4.
Let x be the common factor. Therefore, the angles are 2x, 5x, 7x and 4x.
⇒ 2x + 5x + 7x + 4x = 360°
⇒ 18x = 360°
⇒ x =
⇒ x = 20°
The angles are:
2x = 2 20° = 40°
5x = 5 20° = 100°
7x = 7 20° = 140° (Largest angle)
4x = 4 20° = 80°
Hence, option 3 is the correct option.
In quadrilateral ABCD, ∠A = 45°, ∠B = 55° and ∠D = 60°; the quadrilateral is:
concave
convex
right angled
none of these
Answer
As we know, the sum of all the angles in a quadrilateral is 360°.
In quadrilateral ABCD, ∠A = 45°, ∠B = 55° and ∠D = 60°.
∠A + ∠B + ∠C + ∠D = 360°
⇒ 45° + 55° + ∠C + 60° = 360°
⇒ 160° + ∠C = 360°
⇒ ∠C = 360° - 160°
⇒ ∠C = 200°
According to the definition of a concave polygon, if at least one internal angle of a polygon is more than 180°, then the polygon is concave.
Hence, option 1 is the correct option.
In quadrilateral ABCD, ∠D = 40°, ∠C = 80° AP bisects angle A and BP bisects angle ∠B; then ∠APB is equal:
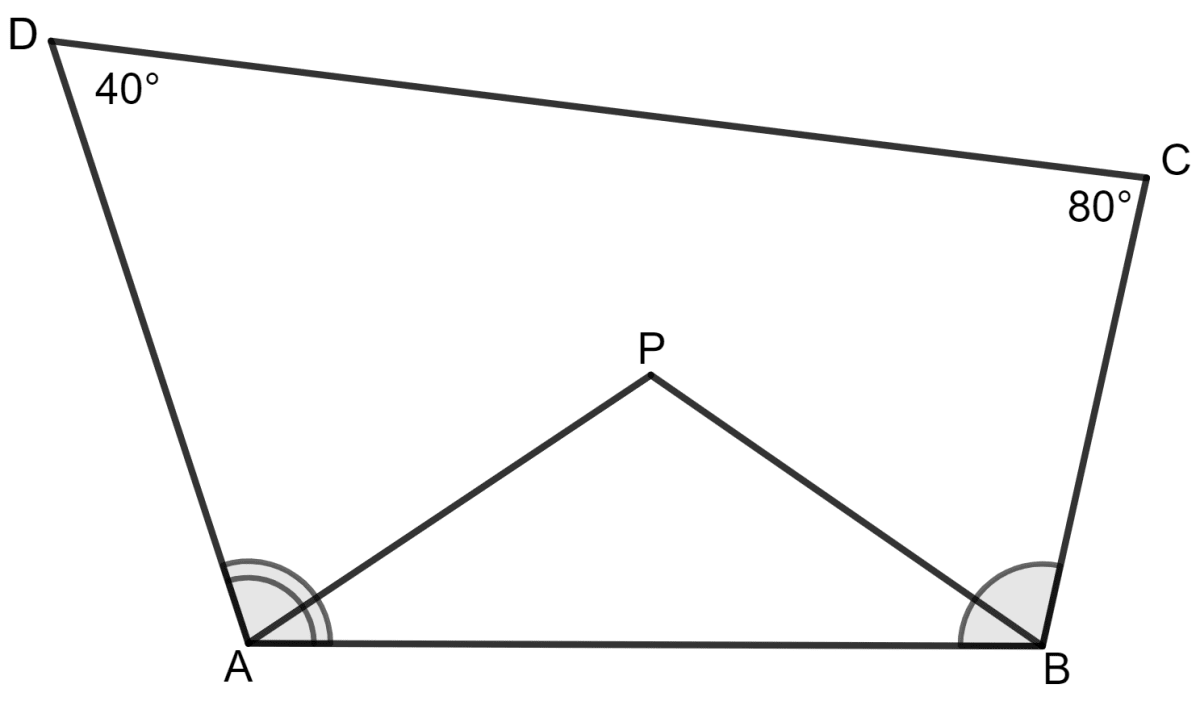
90°
120°
90°
60°
Answer
As we know, the sum of all the angles in a quadrilateral is 360°.
In quadrilateral ABCD, ∠D = 40°, ∠C = 80°.
∠A + ∠B + ∠C + ∠D = 360°
⇒ ∠A + ∠B + 80° + 40° = 360°
⇒ ∠A + ∠B + 120° = 360°
⇒ ∠A + ∠B = 360° - 120°
⇒ ∠A + ∠B = 240°
⇒ (∠A + ∠B) = 240°
⇒ (∠A + ∠B) =
⇒ (∠A + ∠B) = 120°
As we know, the sum of all the angles in a triangle is 180°.
∠PAB + ∠PBA + ∠APB = 180°
⇒ (∠A + ∠B) + ∠APB = 180°
⇒ 120° + ∠APB = 180°
⇒ ∠APB = 180° - 120°
⇒ ∠APB = 60°
Hence, option 4 is the correct option.
The sum of interior angles of a polygon is 900°. The number of side in this polygon is:
5
7
9
11
Answer
According to the properties of a polygon, if there are n sides, then the sum of its interior angles is (2n - 4) x 90°.
So, (2n - 4) x 90° = 900°
⇒ (2n - 4) =
⇒ 2n - 4 = 10
⇒ 2n = 10 + 4
⇒ 2n = 14
⇒ n =
⇒ n = 7
Hence, option 2 is the correct option.
Calculate the sum of angles of a polygon with 10 sides:
Answer
According to the properties of a polygon, if there are n sides, then the sum of its interior angles is (2n - 4) x 90°.
For a polygon with 10 sides:
Sum of angles = (2 x 10 - 4) x 90°
= (20 - 4) x 90°
= 16 x 90°
= 1440°
Hence, sum of angles of polygon is 1440°.
Find the number of sides ina polygon if the sum of its interior angles is 16 right angles.
Answer
According to the properties of a polygon, if there are n sides, then the sum of its interior angles is (2n - 4) x 90°.
It is given that the sum of its interior angles is 16 right angles, which equals 16 x 90° = 1440°.
So,
(2n - 4) x 90° = 1440°
⇒ (2n - 4) =
⇒ 2n - 4 = 16
⇒ 2n = 16 + 4
⇒ 2n = 20
⇒ n =
⇒ n = 10
Hence, the number of sides is 10.
Is it possible to have a polygon whose sum of interior angles is:
(i) 870°
(ii) 2340°
(iii) 7 right angles ?
Answer
(i) 870°
According to the properties of a polygon, if there are n sides, then the sum of its interior angles is (2n - 4) x 90°.
So,
(2n - 4) x 90° = 870°
⇒ (2n - 4) =
⇒ 2n - 4 = 9.66........
⇒ 2n = 9.66.... + 4
⇒ 2n = 13.66....
Since 2n must be an integer, it is not possible for 2n to equal 13.666....
Hence, it is not possible to have a polygon with a sum of interior angles equal to 870°.
(ii) 2340°
According to the properties of a polygon, if there are n sides, then the sum of its interior angles is (2n - 4) x 90°.
So,
(2n - 4) x 90° = 2340°
⇒ (2n - 4) =
⇒ 2n - 4 = 26
⇒ 2n = 26 + 4
⇒ 2n = 30
⇒ n =
⇒ n = 15
Hence, it is possible to have a polygon whose sum of interior angles is 2340°.
(iii) 7 right angles
According to the properties of a polygon, if there are n sides, then the sum of its interior angles is (2n - 4) x 90°.
Given that the sum of its interior angles is 7 right angles:
7 x 90° = 630°
So,
(2n - 4) x 90° = 630°
⇒ (2n - 4) =
⇒ 2n - 4 = 7
⇒ 2n = 7 + 4
⇒ 2n = 11
Since 2n must be an integer, 2n = 11 is not possible.
Hence, it is not possible to have a polygon whose sum of interior angles is 630°.
(i) If all the angles of a hexagon are equal, find the measure of each angle.
(ii) If all the angles of a 14-sided figure are equal, find the measure of each angle.
Answer
(i) According to the properties of a polygon, if a polygon has n sides, then the sum of its interior angles is (2n - 4) x 90°.
A hexagon has 6 sides.
So, the sum of its interior angles is:
(2 x 6 - 4) x 90°
= (12 - 4) x 90°
= 8 x 90°
= 720°
Since it is given that all angles are equal, let each angle be a.
⇒ 6a = 720°
⇒ a =
⇒ a = 120°
Hence, the measure of each angle is 120°.
(ii) According to the properties of a polygon, if a polygon has n sides, then the sum of its interior angles is (2n - 4) x 90°.
A polygon with 14 sides is given.
So, the sum of its interior angles is:
(2 x 14 - 4) x 90°
= (28 - 4) x 90°
= 24 x 90°
= 2160°
Since it is given that all angles are equal, let each angle be a.
14a = 2160°
⇒ a =
⇒ a =
⇒ a =
Hence, the measure of each angle is .
Find the sum of exterior angles obtained on producing the sides of a polygon, in order, with 7 sides.
Answer
According to the property of polygon, the sum of all exterior angles of a polygon is always 360°.
Hence, the sum of the exterior angles obtained by extending the sides of a polygon with 7 sides, in order, is 360°.
The sides of a hexagon are produced in order. If the measures of exterior angles so obtained are (6x - 1)°, (10x + 2)°, (8x+ 2)°, (9x - 3)°, (5x + 4)° and (12x + 6)°, find each exterior angle.
Answer
According to the property of polygons, the sum of all exterior angles of a polygon is always 360°.
So,
(6x - 1)° + (10x + 2)° + (8x + 2)° + (9x - 3)° + (5x + 4)° + (12x + 6)° = 360°
⇒ 6x° - 1° + 10x° + 2° + 8x° + 2° + 9x° - 3° + 5x° + 4° + 12x° + 6° = 360°
⇒ 50x° + 10° = 360°
⇒ 50x° = 360° - 10°
⇒ 50x° = 350°
⇒ x° =
⇒ x = 7°
So, the exterior angles are calculated as follows:
(6x - 1)° = (6 7 - 1)° = (42 - 1)° = 41°
(10x + 2)° = (10 7 + 2)° = (70 + 2)° = 72°
(8x + 2)° = (8 7 + 2)° = (56 + 2)° = 58°
(9x - 3)° = (9 7 - 3)° = (63 - 3)° = 60°
(5x + 4)° = (5 7 + 4)° = (35 + 4)° = 39°
(12x + 6)° = (12 7 + 6)° = (84 + 6)° = 90°
Hence, the exterior angles are 41°, 72°, 58°, 60°, 39° and 90°.
The interior angles of a pentagon are in the ratio 4 : 5 : 6 : 7 : 5. Find each angle of the pentagon.
Answer
According to the properties of polygons, if a polygon has n sides, then the sum of its interior angles is (2n - 4) x 90°.
A pentagon have 5 sides.
So, sum of its interior angles is:
(2 x 5 - 4) x 90°
= (10 - 4) x 90°
= 6 x 90°
= 540°
It is given that the interior angles of the pentagon are in the ratio 4 : 5 : 6 : 7 : 5. Let each angle be a.
So,
4a + 5a + 6a + 7a + 5a = 540°
⇒ 27a = 540°
⇒ a =
⇒ a = 20°
The angles are:
4a = 4 x 20° = 80°
5a = 5 x 20° = 100°
6a = 6 x 20° = 120°
7a = 7 x 20° = 140°
5a = 5 x 20° = 100°
Hence, the measures of the angles are 80°, 100°, 120°, 140° and 100°.
Two angles of a hexagon are 120° and 160°. If the remaining four angles are equal, find each equal angle.
Answer
According to the properties of polygons, if a polygon has n sides, then the sum of its interior angles is (2n - 4) x 90°.
A hexagon have 6 sides.
So, the sum of its interior angles is:
(2 x 6 - 4) x 90°
= (12 - 4) x 90°
= 8 x 90°
= 720°
It is given that two angles of the hexagon are 120° and 160°, and the remaining four angles are equal.
Let each of the equal angles be x°.
So,
120° + 160° + x° + x° + x° + x° = 720°
⇒ 280° + 4x° = 720°
⇒ 4x° = 720° - 280°
⇒ 4x° = 440°
⇒ x° =
⇒ x° = 110°
Hence, the measure of each of the four equal angles in the hexagon is 110°.
The figure given below shows a pentagon ABCDE with sides AB and ED parallel to each other, and ∠B : ∠C : ∠D = 5 : 6 : 7.
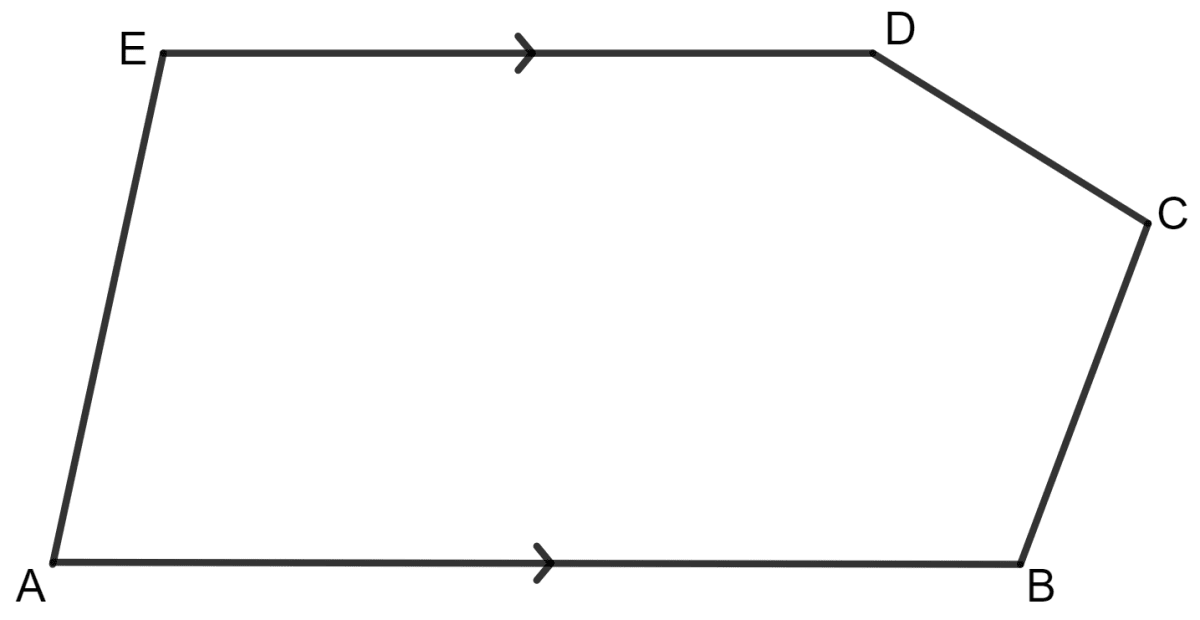
(i) Using formula, find the sum of interior angles of the pentagon.
(ii) Write the value of ∠A + ∠E.
(iii) Find angles B, C and D.
Answer
(i) According to the properties of polygons, if a polygon has n sides, then the sum of its interior angles is (2n - 4) x 90°.
A pentagon has 5 sides.
So, the sum of its interior angles is:
(2 x 5 - 4) x 90°
= (10 - 4) x 90°
= 6 x 90°
= 540°
Hence, the sum of the interior angles of a pentagon is 540°.
(ii) It is given that in pentagon ABCDE, sides AB and ED are parallel to each other.
As we know, corresponding angles are formed when a transversal crosses two parallel lines, and the sum of corresponding angles is 180°.
Hence, ∠A + ∠E = 180°.
(iii) It is given that ∠B : ∠C : ∠D = 5 : 6 : 7.
Let the common factor of the angles be a. So, ∠B = 5a, ∠C = 6a and ∠D = 7a.
Therefore,
⇒ ∠A + ∠B + ∠C + ∠D + ∠E = 540°
⇒ ∠A + 5a + 6a + 7a + ∠E = 540°
⇒ ∠A + ∠E + 18a = 540°
Since the sum of all angles in a pentagon is 540° and we know ∠A + ∠E equals 180°.
⇒ 180° + 18a = 540°
⇒ 18a = 540° - 180°
⇒ 18a = 360°
⇒ a =
⇒ a = 20°
Thus,
∠B = 5a = 5 x 20° = 100°
∠C = 6a = 6 x 20° = 120°
∠D = 7a = 7 x 20° = 140°
Hence, ∠B = 100°, ∠C = 120° and ∠D = 140°.
Two angles of a polygon are right angles and the remaining are 120° each. Find the number of sides in it.
Answer
Given that a polygon has two right angles and the remaining angles are each 120°, we need to find the number of sides of the polygon, denoted as n.
For a polygon with n sides, the sum of its interior angles is (2n - 4) x 90°.
Accordingly:
⇒ 2 x 90° + (n - 2) x 120° = (2n - 4) x 90°
⇒ 180° + 120°n - 240° = 180°n - 360°
⇒ 120°n - 60° = 180°n - 360°
⇒ 180°n - 120°n = 360° - 60°
⇒ 60°n = 300°
⇒ n =
⇒ n = 5
Hence, the number of sides is 5.
In a hexagon ABCDEF, side AB is parallel to side FE and ∠B : ∠C : ∠D : ∠E = 6 : 4 : 2 : 3. Find ∠B and ∠D.
Answer
According to the properties of polygons, if a polygon has n sides, then the sum of its interior angles is (2n - 4) x 90°.
For a hexagon with 6 sides: n = 6
The sum of its interior angles is:
(2 x 6 - 4) x 90°
= (12 - 4) x 90°
= 8 x 90°
= 720° ...............(1)
It is given that hexagon ABCDEF has sides AB and EF parallel to each other.
As we know, corresponding angles are formed when a transversal crosses two lines, and the sum of corresponding angles is 180°. Therefore,
∠A + ∠F = 180° ...............(2)
It is also given that: ∠B : ∠C : ∠D : ∠E = 6 : 4 : 2 : 3.
Let the common factor of the angles be a. Thus, ∠B = 6a, ∠C = 4a, ∠D = 2a and ∠E = 3a.
Using the equations (1) and (2),
⇒ ∠A + ∠B + ∠C + ∠D + ∠E + ∠F = 720°
⇒ ∠A + 6a + 4a + 2a + 3a + ∠F = 720°
⇒ ∠A + ∠F + 15a = 720°
⇒ 180° + 15a = 720°
⇒ 15a = 720° - 180°
⇒ 15a = 540°
⇒ a =
⇒ a = 36°
Thus,
∠B = 6a = 6 x 36° = 216°
∠C = 4a = 4 x 36° = 144°
∠D = 2a = 2 x 36° = 72°
∠E = 3a = 3 x 36° = 108°
Hence, ∠B = 216°and ∠D = 72°.
The angles of a hexagon are x + 10°, 2x + 20°, 2x - 20°, 3x - 50°, x + 40° and x + 20°. Find x.
Answer
According to the properties of a polygon, if a polygon has n sides, then the sum of its interior angles is (2n - 4) x 90°.
For a hexagon with 6 sides, n = 6.
The sum of its interior angles is:
(2 x 6 - 4) x 90°
= (12 - 4) x 90°
= 8 x 90°
= 720°
It is given that the angles of the hexagon are x + 10°, 2x + 20°, 2x - 20°, 3x - 50°, x + 40° and x + 20°.
⇒ ∠A + ∠B + ∠C + ∠D + ∠E + ∠F = 720°
⇒ (x + 10°) + (2x + 20°) + (2x - 20°) + (3x - 50°) + (x + 40°) + (x + 20°) = 720°
⇒ x + 10° + 2x + 20° + 2x - 20° + 3x - 50° + x + 40° + x + 20° = 720°
⇒ 10x + 20° = 720°
⇒ 10x = 720° - 20°
⇒ 10x = 700°
⇒ x =
⇒ x = 70°
Hence, the value of x is 70°.
In a pentagon, two angles are 40° and 60° and the rest are in the ratio 1 : 3 : 7. Find the biggest angle of the pentagon.
Answer
According to the properties of a polygon, if a polygon has n sides, then the sum of its interior angles is (2n - 4) x 90°.
For a pentagon with 5 sides: n = 5
The sum of its interior angles is:
(2 x 5 - 4) x 90°
= (10 - 4) x 90°
= 6 x 90°
= 540°
It is given that in a pentagon, two angles are 40° and 60°, and the remaining three angles are in the ratio 1 : 3 : 7.
Let the pentagon be ABCDE, such that ∠A = 40° and ∠B = 60°
Let the common factor of the remaining angles be a. Thus, the remaining angles are:
∠C = a, ∠D = 3a and ∠E = 7a.
Therefore,
⇒ ∠A + ∠B + ∠C + ∠D + ∠E = 540°
⇒ 40° + 60° + a + 3a + 7a = 540°
⇒ 100° + 11a = 540°
⇒ 11a = 540° - 100°
⇒ 11a = 440°
⇒ a =
⇒ a = 40°
Thus:
∠C = a = 40°
∠D = 3a = 3 x 40° = 120°
∠D = 7a = 7 x 40° = 280°
Hence, the largest angle is 280°.
Each interior angle of a regular polygon is double of its exterior angle, the number of sides in the polygon is.
3
4
6
8
Answer
It is given that each interior angle of a regular polygon is double of its exterior angle.
Let the exterior angle of the polygon be a.
Then the interior angle is 2a.
We know that the sum of the interior angle and the exterior angle is 180°:
⇒ a + 2a = 180°
⇒ 3a = 180°
⇒ a =
⇒ a = 60°
So, the exterior angle is 60° and the interior angle is:
2a = 2 x 60° = 120°
The formula for each interior angle of a regular polygon is:
⇒ 120° =
By cross multiplying, we get
⇒ 120°n = (2n - 4) 90°
⇒ 120°n = 180°n - 360°
⇒ 180°n - 120°n = 360°
⇒ 60°n = 360°
⇒ n =
⇒ n = 6
Hence, option 3 is the correct option.
The sum of all interior angles of a regular polygon is 1260°; then the number of sides in the polygon is.
7
6
9
8
Answer
It is given that the sum of all interior angles of a regular polygon is 1260°.
According to the properties of a polygon, if there are n sides, the sum of its interior angles is (2n - 4) x 90°.
⇒ (2n - 4) x 90° = 1260°
⇒ (2n - 4) =
⇒ 2n - 4 = 14
⇒ 2n = 14 + 4
⇒ 2n = 18
⇒ n =
⇒ n = 9
Hence, option 3 is the correct option.
The sum of all interior angles of a regular polygon is equal to sum of all its exterior angles. The number of sides in the polygon is:
4
5
6
8
Answer
It is given that the sum of all interior angles of a regular polygon is equal to the sum of all its exterior angles.
According to the properties of a polygon, if there are n sides, then the sum of its interior angles is (2n - 4) x 90° and the sum of its exterior angles is 360°.
⇒ (2n - 4) x 90° = 360°
⇒ (2n - 4) =
⇒ (2n - 4) = 4
⇒ 2n = 4 + 4
⇒ 2n = 8
⇒ n =
⇒ n = 4
Hence, option 1 is the correct option.
If each interior angle of a regular polygon is right angle. The number of sides in the polygon is:
4
5
6
8
Answer
It is given that each interior angle of a regular polygon is right angles.
Interior angle =
=
=
= 120°
According to the properties of a polygon, if a polygon has n sides, each of its interior angles is .
⇒ = 120°
By cross multiplying, we get
⇒ (2n - 4) x 90° = 120°n
⇒ 180°n - 360° = 120°n
⇒ 180°n - 120°n = 360°
⇒ 60°n = 360°
⇒ n =
⇒ n = 6
Hence, option 3 is the correct option.
The ratio between each interior angle of a regular polygon and each exterior angle of it is 3 : 2. The number of sides in the polygon is:
6
4
8
none of these
Answer
It is given that the ratio between each interior angle and each exterior angle of a regular polygon is 3 : 2.
Let the common factor be a. Then,
interior angle = 3a and exterior angle = 2a.
Since the sum of an interior angle and an exterior angle is 180°:
⇒ 3a + 2a = 180°
⇒ 5a = 180°
⇒ a =
⇒ a = 36°
Therefore:
Interior angle = 3a = 3 x 36° = 108°
Exterior angle = 2a = 2 x 36° = 72°
According to the properties of a polygon, if a polygon has n sides, each of its exterior angles is .
⇒ = 72°
By cross multiplying, we get
⇒ 360° = 72°n
⇒ n =
⇒ n = 5
Hence, option 4 is the correct option.
Fill in the blanks:
Incase of regular polygon, with:
| no. of sides | each exterior angle | each interior angle |
|---|---|---|
| (i) ..8............ | ............... | ............... |
| (ii)..12..... | ............... | ............... |
| (iii) ............... | ..72°.......... | ............... |
| (iv) ............... | ..45°.......... | ............... |
| (v) ............... | ............... | ....150°....... |
| (vi) ............... | ............... | ....140°....... |
Answer
(i) As per the properties of polygon, if there are n number of sides then each of its exterior angles is .
n = 8
⇒ = 45°
Hence, each exterior angle = 45°.
As per the properties of polygon, if there are n number of sides then each of its interior angles is .
=
=
=
=
= 135°
Hence, each interior angle = 135°.
(ii) As per the properties of polygon, if there are n number of sides then each of its exterior angles is .
n = 12
⇒ = 30°
Hence, each exterior angle = 30°.
As per the properties of polygon, if there are n number of sides then each of its interior angles is .
=
=
=
=
= 150°
Hence, each interior angle = 150°.
(iii) As per the properties of polygon, if there are n number of sides then each of its exterior angles is .
Exterior angle = 72°
⇒ = 72°
⇒ n =
⇒ n = 5
Hence, number of sides = 5.
As per the properties of polygon, if there are n number of sides then each of its interior angles is .
n = 5
=
=
=
=
= 108°
Hence, each interior angle = 108°.
(iv) As per the properties of polygon, if there are n number of sides then each of its exterior angles is .
Exterior angle = 45°
⇒ = 45°
⇒ n =
⇒ n = 8
Hence, number of sides = 8.
As per the properties of polygon, if there are n number of sides then each of its interior angles is .
n = 8
=
=
=
=
= 135°
Hence, each interior angle = 135°.
(v) As per the properties of polygon, if there are n number of sides then each of its interior angles is .
⇒ = 150°
⇒ (2n - 4) x 90° = 150°n
⇒ 180°n - 360° = 150°n
⇒ 180°n - 150°n = 360°
⇒ 30°n = 360°
⇒ n =
⇒ n = 12
Hence, number of sides = 12.
As per the properties of polygon, if there are n number of sides then each of its exterior angles is
⇒ = 30°
Hence, each exterior angle = 30°.
(vi) As per the properties of polygon, if there are n number of sides then each of its interior angles is .
⇒ = 140°
⇒ (2n - 4) x 90° = 140°n
⇒ 180°n - 360° = 140°n
⇒ 180°n - 140°n = 360°
⇒ 40°n = 360°
⇒ n =
⇒ n = 9
Hence, number of sides = 9.
As per the properties of polygon, if there are n number of sides then each of its exterior angles is .
⇒ = 40°
Hence, each exterior angle = 40°.
| no. of sides | each exterior angle | each interior angle |
|---|---|---|
| (i) 8 | 45° | 135° |
| (ii) 12 | 30° | 150° |
| (iii) 5 | 72° | 108° |
| (iv) 8 | 45° | 135° |
| (v) 12 | 30° | 150° |
| (vi) 9 | 40° | 140° |
Find the number of sides in a regular polygon, if its each interior angle is:
(i) 160°
(ii) 135°
(iii) of a right angle.
Answer
(i) 160°
According to the properties of a polygon, if there are n sides, then each of its interior angles is .
Given that each interior angle is 160°,
= 160°
By cross multiplying, we get
⇒ (2n - 4) x 90° = 160°n
⇒ 180°n - 360° = 160°n
⇒ 180°n - 160°n = 360°
⇒ 20°n = 360°
⇒ n =
⇒ n = 18
Hence, the number of sides is 18.
(ii) 135°
According to the properties of a polygon, if there are n sides, then each of its interior angles is .
Given that each interior angle is 135°,
⇒ = 135°
By cross multiplying, we get
⇒ (2n - 4) x 90° = 135°n
⇒ 180°n - 360° = 135°n
⇒ 180°n - 135°n = 360°
⇒ 45°n = 360°
⇒ n =
⇒ n = 8
Hence, the number of sides is 8.
(iii) of a right angle.
= x 90°
=
= 108°
According to the properties of a polygon, if there are n sides, then each of its interior angles is .
Given that each interior angle is 108°,
⇒ = 108°
By cross multiplying, we get
⇒ (2n - 4) x 90° = 108°n
⇒ 180°n - 360° = 108°n
⇒ 180°n - 108°n = 360°
⇒ 72°n = 360°
⇒ n =
⇒ n = 5
Hence, the number of sides is 5.
Find the number of sides in a regular polygon, if its each exterior angle is:
(i) of a right angle
(ii) two-fifths of a right angle
Answer
(i) of a right angle
= x 90°
=
= 30°
According to the properties of a polygon, if there are n sides, then each of its exterior angles is .
Given that each exterior angle is 30°,
⇒ = 30°
⇒ n =
⇒ n = 12
Hence, the number of sides is 12.
(ii) Two-fifths of a right angle,
= x 90°
=
= 36°
According to the properties of a polygon, if there are n sides, then each of its exterior angles is .
Given that each exterior angle is 36°,
⇒ = 36°
⇒ n =
⇒ n = 10
Hence, the number of sides is 10.
Is it possible to have a regular polygon whose each interior angle is:
(i) 170°
(ii) 138°
Answer
(i) 170°
According to the properties of a polygon, if there are n sides, then each of its interior angles is .
Given that each interior angle is 170°,
⇒ = 170°
⇒ (2n - 4) x 90° = 170°n
⇒ 180°n - 360° = 170°n
⇒ 180°n - 170°n = 360°
⇒ 10°n = 360°
⇒ n =
⇒ n = 36
Hence, a regular polygon is possible when each interior angle is 170°.
(ii) 138°
According to the properties of a polygon, if there are n sides, then each of its interior angles is .
Given that each interior angle is 138°,
⇒ = 138°
⇒ (2n - 4) x 90° = 138°n
⇒ 180°n - 360° = 138°n
⇒ 180°n - 138°n = 360°
⇒ 42°n = 360°
⇒ n =
⇒ n =
⇒ n =
Hence, a regular polygon is not possible when each interior angle is 138°.
Is it possible to have a regular polygon whose each exterior angle is:
(i) 80°
(ii) 40% of a right angle
Answer
(i) 80°
According to the properties of a polygon, if there are n sides, then each of its exterior angles is .
Given that each exterior angle is 80°,
⇒ = 80°
⇒ n =
⇒ n = 4.5
Hence, a regular polygon is not possible when each exterior angle is 80°.
(ii) 40% of a right angle is:
= 40% x 90°
=
=
= 36°
According to the properties of a polygon, if there are n sides, then each of its exterior angles is .
Given that each exterior angle is 36°,
⇒ = 36°
⇒ n =
⇒ n = 10
Hence, a regular polygon is possible when each exterior angle is 40% of a right angle.
Find the number of sides in a regular polygon, if its interior angle is equal to its exterior angle.
Answer
It is given that the interior angle is equal to the exterior angle.
Let the exterior angle be a. Therefore, the interior angle is also a.
We know that the sum of an interior angle and its corresponding exterior angle is 180°,
⇒ a + a = 180°
⇒ 2a = 180°
⇒ a =
⇒ a = 90°
Thus, both the interior angle and the exterior angle are 90°.
According to the properties of a polygon, if there are n sides, then each of its interior angles is .
⇒ = 90°
By cross-multiplying, we get
⇒ (2n - 4) x 90° = 90°n
⇒ 180°n - 360° = 90°n
⇒ 180°n - 90°n = 360°
⇒ 90°n = 360°
⇒ n =
⇒ n = 4
Hence, the number of sides is 4.
The exterior angle of a regular polygon is one third of its interior angle. Find the number of sides in the polygon.
Answer
It is given that the exterior angle of a regular polygon is one-third of its interior angle.
Let the interior angle be a. Then, the exterior angle is .
We know that the sum of the interior and exterior angles is 180°,
⇒ a + = 180°
⇒ + = 180°
⇒ = 180°
⇒ = 180°
⇒ a =
⇒ a =
⇒ a = 135°
So, the interior angle is 135°, and the exterior angle is:
= = 45°
According to the properties of polygons, each interior angle of a regular polygon with n sides is .
⇒ = 135°
⇒ (2n - 4) x 90° = 135°n
⇒ 180°n - 360° = 135°n
⇒ 180°n - 135°n = 360°
⇒ 45°n = 360°
⇒ n =
⇒ n = 8
Hence, the number of sides is 8.
The measure of each interior angle of a regular polygon is five times the measure of its exterior angle. Find:
(i) measure of each interior angle,
(ii) measure of each exterior angle and
(iii) number of sides in the polygon
Answer
(i) It is given that each interior angle of a regular polygon is five times the measure of its exterior angle.
Let the exterior angles of the polygon be a.
Then, the interior angle = 5 x a = 5a
We know that the sum of the interior angle and the exterior angle is 180°.
⇒ a + 5a = 180°
⇒ 6a = 180°
⇒ a =
⇒ a = 30°
So, the exterior angle is 30°.
The interior angle = 5a = 5 x 30° = 150°
Hence, the interior angle of the polygon is 150°.
(ii) Exterior angle = a = 30°
Hence, the exterior angle of the polygon is 30°.
(iii) According to the properties of polygons, each interior angle of a regular polygon with n sides is .
⇒ = 150°
⇒ (2n - 4) x 90° = 150°n
⇒ 180°n - 360° = 150°n
⇒ 180°n - 150°n = 360°
⇒ 30°n = 360°
⇒ n =
⇒ n = 12
Hence, the number of sides of the polygon is 12.
The ratio between the interior angle and the exterior angle of a regular polygon is 2 : 1. Find.
(i) each exterior angle of the polygon,
(ii) number of sides in the polygon.
Answer
(i) It is given that the ratio between the interior angle and the exterior angle of a regular polygon is 2 : 1.
Let the common factor be a.
Then:
Interior angles = 5 x a = 2a
Exterior angles = 1 x a = a
We know that sum of the interior angle and the exterior angle is 180°.
⇒ 2a + a = 180°
⇒ 3a = 180°
⇒ a =
⇒ a = 60°
Thus:
Interior angle = 2a = 2 x 60° = 120°
Exterior angle = a = 60°
Hence, the exterior angle of the polygon is 60°.
(ii) According to the properties of polygons, each interior angle of a regular polygon with n sides is .
⇒ = 120°
By cross-multiplying, we get
⇒ (2n - 4) x 90° = 120°n
⇒ 180°n - 360° = 120°n
⇒ 180°n - 120°n = 360°
⇒ 60°n = 360°
⇒ n =
⇒ n = 6
Hence, the number of sides is 6.
The ratio between the exterior angle and the interior angle of a regualr polygon is 1 : 4. Find the number of sides in the polygon.
Answer
It is given that the ratio between the exterior angle and the interior angle of a regular polygon is 1 : 4.
Let the common factor be a.
Then:
Interior angle = 4 x a = 4a
Exterior angle = 1 x a = a
We know that sum of the interior angle and the exterior angle is 180°.
⇒ 4a + a = 180°
⇒ 5a = 180°
⇒ a =
⇒ a = 36°
Thus:
Interior angle = 4a = 4 x 36° = 144°
Exterior angle = a = 36°
According to the properties of polygons, each interior angle of a regular polygon with n sides is
⇒ = 144°
By cross-multiplying, we get
⇒ (2n - 4) x 90° = 144°n
⇒ 180°n - 360° = 144°n
⇒ 180°n - 144°n = 360°
⇒ 36°n = 360°
⇒ n =
⇒ n = 10
Hence, the number of sides is 10.
The sum of interior angles of a regular polygon is twice the sum of its exterior angles. Find the number of sides of the polygon.
Answer
It is given that the sum of interior angles of a regular polygon is twice the sum of its exterior angles.
Let the sum of the exterior angles be a.
Then, the sum of the interior angles is 2a.
We know that sum of the interior angle and the exterior angle is 180°.
⇒ 2a + a = 180°
⇒ 3a = 180°
⇒ a =
⇒ a = 60°
Thus:
Exterior angle = a = 60°
Interior angle = 2a = 2 x 60° = 120°
According to the properties of polygons, each interior angle of a regular polygon with n sides is .
⇒ = 120°
By cross-multiplying, we get
⇒ (2n - 4) x 90° = 120°n
⇒ 180°n - 360° = 120°n
⇒ 180°n - 120°n = 360°
⇒ 60°n = 360°
⇒ n =
⇒ n = 6
Hence, the number of sides is 6.
AB, BC and CD are three consecutive sides of a regular polygon. If angle BAC = 20°, find:
(i) its each interior angle
(ii) its each exterior angle
(iii) the number of sides in the polygon.
Answer
(i) As it is given that the polygon is regular,
AB = BC
∠ BCA = ∠ BAC
∠ BCA = 20°
Thus, ∠ BAC = 20°
In triangle ABC, the sum of all angles is 180°.
∠ BAC + ∠ BCA + ∠ CBA = 180°
⇒ 20° + 20° + ∠ CBA = 180°
⇒ 40° + ∠ CBA = 180°
⇒ ∠ CBA = 180° - 40°
⇒ ∠ CBA = 140°
Hence, each interior angle is 140°.
(ii) As we know that sum of the interior angle and the exterior angle of a polygon is 180°.
Thus, Exterior angle = 180° - Interior angle
= 180° - 140°
= 40°
Hence, each exterior angle is 40°.
(iii) According to the properties of polygons, each interior angle of a regular polygon with n sides is .
⇒ = 140°
By cross-multiplying, we get
⇒ (2n - 4) x 90° = 140°n
⇒ 180°n - 360° = 140°n
⇒ 180°n - 140°n = 360°
⇒ 40°n = 360°
⇒ n =
⇒ n = 9
Hence, the number of sides is 9.
Two alternate sides of a regular polygon, when produced, meet at right angle. Calculate the number of sides in the polygon.
Answer
Let the measure of each exterior angle be x and the number of sides be n. Therefore we can write:
n =
Given that:
⇒ 2x + 90° = 180°
⇒ 2x = 180° - 90°
⇒ 2x = 90°
⇒ x =
⇒ x = 45°
Using x = 45° to find n:
⇒ = 45°
⇒ n =
⇒ n = 8
Hence, the number of sides is 8.
In a regular pentagon ABCDE, draw a diagonal BE and then find the measure of:
(i) ∠BAE
(ii) ∠ABE
(iii) ∠BED
Answer
(i) Since number of sides in the pentagon is 5,
Each exterior angle =
=
= 72°
According to the property of polygons, the sum of an interior angle and its corresponding exterior angle is 180°.
⇒ ∠BAE + 72° = 180°
⇒ ∠BAE = 180° - 72°
⇒ ∠BAE = 108°
Hence, the value of ∠BAE is 108°.
(ii) In triangle ABE, AB = AE.
Therefore, ∠ABE = ∠AEB.
We also know that the sum of all the angles in a triangle is 180°.
⇒ ∠BAE + ∠ABE + ∠AEB = 180°
⇒ 108° + ∠ABE + ∠ABE = 180°
⇒ 108° + 2∠ABE = 180°
⇒ 2∠ABE = 180° - 108°
⇒ 2∠ABE = 72°
⇒ ∠ABE =
⇒ ∠ABE = 36°
Hence, the value of ∠ABE is 36°.
(iii) Since ∠AED = 108° [As each interior angle of the pentagon is 108°],
⇒ ∠AEB = 36°
Therefore,
∠BED = 108° - 36° = 72°
Hence, the value of ∠BED is 72°.
The ratio between the number of sides of two regular polygons is 3 : 4 and the ratio between the sum of their interior angles is 2 : 3. Find the number of sides in each polygon.
Answer
It is given that the ratio between the number of sides of two regular polygons is 3 : 4.
Let the number of sides of the first polygon be 3n and the number of sides of the second polygon be 4n.
The sum of the interior angles of a polygon is (2n - 4) x 90°.
Sum of interior angles of the first polygon = (2 x 3n - 4) x 90°
= (6n - 4) x 90°
Sum of interior angles of the second polygon = (2 x 4n - 4) x 90°
= (8n - 4) x 90°
It is also given that the ratio between the sum of their interior angles is 2 : 3.
By cross multiplying, we get
⇒ 3(6n - 4) = 2(8n - 4)
⇒ 18n - 12 = 16n - 8
⇒ 18n - 16n = 12 - 8
⇒ 2n = 4
⇒ n =
⇒ n = 2
The number of sides of the first polygon is = 3n = 3 x 2 = 6
The number of sides of the second polygon is = 4n = 4 x 2 = 8
Hence, the number of sides are 6 and 8.
Three of the exterior angles of a hexagon are 40°, 51° and 86°. If each of the remaining exterior angles is x°, find the value of x.
Answer
It is given that three of the exterior angles of a hexagon are 40°, 51° and 86°, and each of the remaining exterior angles is x°.
According to the properties of polygons, the sum of the exterior angles of any polygon is 360°.
Thus,
⇒ 40° + 51° + 86° + x° + x° + x° = 360°
⇒ 177° + 3x° = 360°
⇒ 3x° = 360° - 177°
⇒ 3x° = 183°
⇒ x° =
⇒ x° = 61°
Hence, the value of x is 61°.
Calculate the number of sides of a regular polygon if:
(i) its interior angle is five times its exterior angle.
(ii) the ratio between its exterior angle and interior angle is 2 : 7.
(iii) its exterior angle exceeds its interior angle by 60°.
Answer
(i) It is given that the interior angle of a polygon is five times its exterior angle.
Let the exterior angle be a. Then, the interior angle is 5a.
Since the sum of the interior angle and exterior angle is 180°.
⇒ 5a + a = 180°
⇒ 6a = 180°
⇒ a =
⇒ a = 30°
Thus, the exterior angle is 30° and the interior angle is 5a = 5 x 30° = 150°.
According to the properties of polygons, if a polygon has n sides, then each of its interior angles is .
⇒ = 150°
⇒ (2n - 4) x 90° = 150°n
⇒ 180°n - 360° = 150°n
⇒ 180°n - 150°n = 360°
⇒ 30°n = 360°
⇒ n =
⇒ n = 12
Hence, the number of sides is 12.
(ii) It is given that the ratio between the exterior angle and the interior angle is 2 : 7.
Let the exterior angle be 2a. Thus, the interior angle is 7a.
Since the sum of the interior angle and exterior angle is 180°.
⇒ 2a + 7a = 180°
⇒ 9a = 180°
⇒ a =
⇒ a = 20°
Thus, the exterior angle is 2a = 2 x 20° = 40° and the interior angle is 7a = 7 x 20° = 140°.
According to the properties of polygons, if a polygon has n sides, then each of its interior angles is .
⇒ = 140°
⇒ (2n - 4) x 90° = 140°n
⇒ 180°n - 360° = 140°n
⇒ 180°n - 140°n = 360°
⇒ 40°n = 360°
⇒ n =
⇒ n = 9
Hence, the number of sides is 9.
(iii) It is given that the exterior angle of a polygon exceeds its interior angle by 60°.
Let the interior angle be a. Therefore, the exterior angle = 60° + a.
Since the sum of the interior angle and the exterior angle is 180°.
⇒ a + (60° + a) = 180°
⇒ a + 60° + a = 180°
⇒ 2a + 60° = 180°
⇒ 2a = 180° - 60°
⇒ 2a = 120°
⇒ a =
⇒ a = 60°
Thus, the interior angle is 60° and the exterior angle is:
a + 60° = 60° + 60° = 120°
According to the properties of polygons, if a polygon has n sides, each of its interior angles is .
⇒ = 60°
⇒ (2n - 4) x 90° = 60°n
⇒ 180°n - 360° = 60°n
⇒ 180°n - 60°n = 360°
⇒ 120°n = 360°
⇒ n =
⇒ n = 3
Hence, the number of sides is 3.
Each interior angle of a regular polygon is 165°. The number of sides in the polygon is :
12
24
20
6
Answer
It is given that the interior angle of a regular polygon is 165°.
According to the properties of polygons, if a polygon has n sides, then each of its interior angles is .
⇒ = 165°
⇒ (2n - 4) x 90° = 165°n
⇒ 180°n - 360° = 165°n
⇒ 180°n - 165°n = 360°
⇒ 15°n = 360°
⇒ n =
⇒ n = 24
Hence, option 2 is the correct option.
Two angles of a quadrilateral are of 50° each and the other two angles are also equal. The measure of each of these equal angles is:
130°
310°
155°
none of these
Answer
It is given that two angles of a quadrilateral are each 50°, and the other two angles are equal.
We know that the sum of all angles in a quadrilateral is 360°.
Let the other two angles be x°. So,
⇒ 50° + 50° + x° + x° = 360°
⇒ 100° + 2x° = 360°
⇒ 2x° = 360° - 100°
⇒ 2x° = 260°
⇒ x° =
⇒ x° = 130°
Hence, option 1 is the correct option.
A polygon has n sides, the number of diagonals in this polygon is:
Answer
It is given that the polygon has n sides.
By joining any two opposite vertices of the polygon, we obtain diagonal of the polygon.
Total number of ways to join any two vertices (whether adjacent or not) is given by:
= nC2 - n
=
=
=
=
=
=
Hence, option 3 is the correct option.
The interior angle of a regular polygon is four times its exterior angle. The number of sides in the polygon is:
12
10
15
18
Answer
It is given the interior angle of a regular polygon is four times its exterior angle.
Let exterior angle be a. Then, the interior angle is 4a.
We know that the sum of the interior angle and the exterior angle is 180°.
⇒ a + 4a = 180°
⇒ 5a = 180°
⇒ a =
⇒ a = 36°
So, the exterior angle is 36° and the interior angle is:
4a = 4 x 36° = 144°
According to the properties of a polygon, if a polygon has n sides, then each of its interior angles is .
⇒ = 144°
⇒ (2n - 4) x 90° = 144°n
⇒ 180°n - 360° = 144°n
⇒ 180°n - 144°n = 360°
⇒ 36°n = 360°
⇒ n =
⇒ n = 10
Hence, option 2 is the correct option.
Two angles of a quadrilateral are 69° and 113°. If the other two angles are equal then each of equal angles is:
89°
178°
98°
none of these
Answer
It is given that two angles of a quadrilateral are 69° and 113°, and the other two angles are equal.
As we know, the sum of all angles in a quadrilateral is 360°.
Let the equal angles be x°.
⇒ 69° + 113° + x° + x° = 360°
⇒ 182° + 2x° = 360°
⇒ 2x° = 360° - 182°
⇒ 2x° = 178°
⇒ x° =
⇒ x° = 89°
Hence, option 1 is the correct option.
Statement 1: A polynomial whose one or more interior angle is less than two right angles is called a convex polygon.
Statement 2: The line joining any two consecutive vertex of a triangle of a polygon is called its diagonal.
Which of the following options is correct?
Both the statements are true.
Both the statements are false.
Statement 1 is true, and statement 2 is false.
Statement 1 is false, and statement 2 is true.
Answer
A convex polygon is defined as a polygon in which all interior angles are less than 180°.
The statement suggests that if one or more interior angles are less than 180°, the polygon is convex. However, this is not sufficient. For a polygon to be convex, all interior angles must be less than 180°.
So, statement 1 is false.
A diagonal of a polygon is defined as a line segment connecting two non-consecutive vertices.
The line joining two consecutive vertices is simply a side of the polygon, not a diagonal.
So, statement 2 is false.
∴ Both the statements are false.
Hence, option 2 is the correct option.
Assertion (A) : It is possible to have a regular polygon the sum of whose interior angle is 1000°.
Reason (R) : The sum of the interior angle of a polygon with n sides = (2n - 4) x 90°.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
The sum of the interior angles S of a polygon with n sides is given by the formula:
S = (n - 2) x 180°
= (n - 2) x 2 x 90°
= (2n - 4) x 90°.
So, reason (R) is true.
If the sum of the interior angles is 1000°, let the polygon have n sides. Substituting this into the formula :
⇒ 1000° = (n - 2) x 180°
⇒ 1000° = 180°n - 360°
⇒ 180°n = 1000° + 360°
⇒ 180°n = 1360°
⇒ n =
⇒ n = 7.55.....
Since, n must be a whole number, there is no integer value of n that satisfies this equation.
So, assertion (A) is false.
∴ A is false, but R is true.
Hence, option 4 is the correct option.
Assertion (A) : The sum of the interior angle of a regular polygon is thrice the sum of its exterior angle. The polygon is called an octagon.
Reason (R) : Each interior angle of a regular polygon = .
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
Given, the sum of the interior angle of a regular polygon is thrice the sum of its exterior angle.
The sum (S) of the interior angles of a polygon with n sides is given by the formula :
S = (n - 2) x 180°
The sum of the exterior angles = 360°
The sum of the interior angle = 3 x The sum of the exterior angles
⇒ (n - 2) x 180° = 3 x 360°
⇒ (n - 2) x 180° = 1080°
⇒ n - 2 =
⇒ n - 2 = 6
⇒ n = 6 + 2
⇒ n = 8
Thus, the polygon is octagon.
So, assertion (A) is true.
The sum of the interior angles of a polygon with n sides is given by the formula :
S = (n - 2) x 180°
Since, in a regular polygon each interior angle is equal.
∴ Each interior angle =
So, reason (R) is true.
∴ Both A and R are correct, and R is not the correct explanation for A.
Hence, option 2 is the correct option.
Assertion (A) : The number of diagonals of a nonagon = 27.
Reason (R) : The number of diagonals of an n-sided polygon = .
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
The number of diagonals (D) in an n-sided polygon is given by the formula,
D =
For nonagon, n = 9
D = = 27.
So, assertion (A) is true.
Simplifying the formula for no. of diagonals,
So, reason (R) is true.
∴ Both A and R are correct, and R is the correct explanation for A.
Hence, option 1 is the correct option.
Assertion (A) : The ratio between the exterior and interior angle of a regular polygon is 1 : 8. The number of sides of the regular polygon is 18.
Reason (R) : The sum of the exterior angle and interior angles of a convex polygon are 360° and 2(n - 1) x 90° respectively.
Both A and R are correct, and R is the correct explanation for A.
Both A and R are correct, and R is not the correct explanation for A.
A is true, but R is false.
A is false, but R is true.
Answer
Let each interior angle be I and exterior angle be E.
Given, the ratio between the exterior and interior angle of a regular polygon is 1 : 8.
⇒ I = 8E
For any polygon, the exterior and interior angles at each vertex are supplementary,
⇒ I + E = 180°
⇒ 8E + E = 180°
⇒ 9E = 180°
⇒ E = = 20°
⇒ I = 8E = 8 x 20° = 160°
The exterior angle E of a regular polygon with n sides is given by :
⇒ E =
⇒ 20° =
⇒ n =
⇒ n = 18.
So, assertion (A) is true.
We know that,
The sum of exterior angles = 360°.
The sum of interior angles = (n - 2) x 180° = 2(n - 2) x 90°.
So, reason (R) is false.
∴ A is true, but R is false.
Hence, option 3 is the correct option.
The angles of a quadrilateral are in the ratio 3 : 5 : 7. If the difference between the largest and the smallest of these angles is 76°; find the fourth angle of the quadrilateral.
Answer
It is given that the angles of a quadrilateral are in the ratio 3 : 5 : 7.
Let the three angles of the quadrilateral be 3a, 5a and 7a.
The difference between the largest and the smallest of these angles is 76°.
Largest angle = 7a
Smallest angle = 3a
So,
⇒ 7a - 3a = 76°
⇒ 4a = 76°
⇒ a =
⇒ a = 19°
Three angles are 3a, 5a and 7a
⇒ 3 x 19°, 5 x 19° and 7 x 19°
⇒ 57°, 95° and 133°
As we know, the sum of all angles of quadrilateral is 360°.
⇒ 57° + 95° + 133° + x° = 360°
⇒ 285° + x° = 360°
⇒ x° = 360° - 285°
⇒ x° = 75°
Hence, the fourth angle is 75°.
Three angles of a quadrilateral are in the ratio 4 : 5 : 6. The sum of the least and the greatest of these angles is 160°. Find all the angles of the quadrilateral.
Answer
It is given that the angles of a quadrilateral are in the ratio 4 : 5 : 6.
Let the three angles of the quadrilateral be 4a, 5a and 6a.
The sum of the least and the greatest of these angles is 160°.
Largest angle = 6a
Smallest angle = 4a
So,
⇒ 6a + 4a = 160°
⇒ 10a = 160°
⇒ a =
⇒ a = 16°
The three angles are 4a, 5a and 6a
⇒ 4 x 16°, 5 x 16° and 6 x 16°
⇒ 64°, 80° and 96°
As we know, the sum of all angles of quadrilateral is 360°.
⇒ 64° + 80° + 96° + x° = 360°
⇒ 240° + x° = 360°
⇒ x° = 360° - 240°
⇒ x° = 120°
Hence, the angles are 64°, 80°, 96° and 120°.
The sum of three angles of a quadrilateral is 5 times the fourth angle. Find the fourth angles.
Answer
It is given that the sum of three angles of a quadrilateral is 5 times the fourth angle.
Let the fourth angle be a°.
So, the sum of the three angles is 5a°.
As we know that the sum of all angles of quadrilateral is 360°.
⇒ 5a° + a° = 360°
⇒ 6a° = 360°
⇒ a° =
⇒ a° = 60°
Hence, the fourth angle is 60°.
A heptagon has four angles each of 132° and remaining three angles are equal. Find the size of each of the three angles.
Answer
It is given that a heptagon has four angles each of 132° and the remaining three angles are equal.
According to the properties of a polygon, if a polygon has n sides, then each of its interior angles is (2n - 4) x 90°.
Heptagon has 7 sides, so n = 7,
= (2 x 7 - 4) x 90°
= (14 - 4) x 90°
= 10 x 90°
= 900°
The sum of interior angles of the heptagon is 900°.
Let each of the three equal angles be x°.
So,
⇒ 132° + 132° + 132° + 132° + x° + x° + x° = 900°
⇒ 528° + 3x° = 900°
⇒ 3x° = 900° - 528°
⇒ 3x° = 372°
⇒ x° =
⇒ x° = 124°
Hence, each of the three equal angles is 124°.
Each interior angle of a regular polygon is 144°. Find the interior angle of a regular polygon which has double the number of sides as the first polygon.
Answer
It is given that each interior angle of a regular polygon is 144°.
According to the properties of polygons, if a regular polygon has n sides, each of its interior angles .
⇒ = 144°
⇒ (2n - 4) x 90° = 144°n
⇒ 180°n - 360° = 144°n
⇒ 180°n - 144°n = 360°
⇒ 36°n = 360°
⇒ n =
⇒ n = 10
So, the first polygon has 10 sides.
The number of sides of the second polygon is double that of the first polygon:
n = 2 x 10 = 20
For this second polygon, each of its interior angles is .
⇒ Angle =
=
=
=
= 162°
Hence, the interior angle of the second polygon is 162°.
The exterior angles of a pentagon are in the ratio 1 : 2 : 3 : 4 : 5. Find its interior angles.
Answer
It is given that the exterior angles of a pentagon are in the ratio 1 : 2 : 3 : 4 : 5.
Let the exterior angles be a, 2a, 3a, 4a and 5a.
According to the properties of a polygon, the sum of the exterior angles is 360°.
⇒ a + 2a + 3a + 4a + 5a = 360°
⇒ 15a = 360°
⇒ a =
⇒ a = 24°
The exterior angles are,
= 24°, 2 x 24°, 3 x 24°, 4 x 24° and 5 x 24°
= 24°, 48°, 72°, 96° and 120°
The interior angles are calculated by subtracting the exterior angles from 180°:
180° - 24° = 156°
180° - 48° = 132°
180° - 72° = 108°
180° - 96° = 84°
180° - 120° = 60°
Hence, the interior angles are 60°, 84°, 108°, 132° and 156°.
The angles of a pentagon are x°, (x - 10)°, (x + 20)°, (2x - 44)° and (2x - 70)°. Find the value of x.
Answer
It is given that the angles of a pentagon are x°, (x - 10)°, (x + 20)°, (2x - 44)° and (2x - 70)°.
According to the properties of a polygon, the sum of the interior angles of a polygon is (2n - 4) x 90°.
For a pentagon, n = 5.
= (2 x 5 - 4) x 90°
= (10 - 4) x 90°
= 6 x 90°
= 540°
So, the sum of the interior angles of the pentagon is 540°.
So,
⇒ x° + (x - 10)° + (x + 20)° + (2x - 44)° + (2x - 70)° = 540°
⇒ x° + x° - 10° + x° + 20° + 2x° - 44° + 2x° - 70° = 540°
⇒ - 104° + 7x° = 540°
⇒ 7x° = 540° + 104°
⇒ 7x° = 644°
⇒ x° =
⇒ x° = 92°
Hence, the value of x is 92°.
In quadrilateral ABCD, sides AB and DC are parallel to each other. If ∠A : ∠D = 2 : 3 and ∠B : ∠C = 7 : 8; find all the angles of quadrilateral ABCD.
Answer
It is given that in quadrilateral ABCD, the ratio of ∠A to ∠D is 2 : 3.
Let ∠A and ∠D be 2x and 3x, respectively.
Since, AB is parallel to DC, the sum of the interior angles on the same side of the transversal line is 180°.
Thus:
∠A + ∠D = 180°
⇒ 2x + 3x = 180°
⇒ 5x = 180°
⇒ x =
⇒ x = 36°
∠A = 2x = 2 x 36° = 72°
∠D = 3x = 3 x 36° = 108°
It is also given that the ratio of ∠B to ∠C is 7 : 8.
Let ∠B and ∠C be 7y and 8y, respectively.
Since AB is parallel to DC, the sum of the interior angles on the same side of the transversal line is 180°.
Thus:
∠B + ∠C = 180°
⇒ 7y + 8y = 180°
⇒ 15y = 180°
⇒ y =
⇒ y = 12°
∠B = 7y = 7 x 12° = 84°
∠D = 8y = 8 x 12° = 96°
Hence, the angles of the quadrilateral are ∠A = 72°, ∠B = 84°, ∠C = 96° and ∠D = 108°.
In quadrilateral ABCD; 2∠A = 3∠B = 2∠C = 6∠D. Find all the angles of the quadrilateral.
Answer
It is given that in quadrilateral ABCD, 2∠A = 3∠B = 2∠C = 6∠D.
Let 2∠A = 3∠B = 2∠C = 6∠D = 6k (where 6k is the L.C.M. of 2, 3, and 6).
Now, 2∠A = 6k
∠A =
∠A = 3k ...............(1)
Similarly, 3∠B = 6k
∠B =
∠B = 2k ...............(2)
2∠C = 6k
∠C =
∠C = 3k ...............(3)
And, 6∠D = 6k
∠D =
∠D = k ...............(4)
As we know, the sum of all angles in a quadrilateral is 360°.
So,
⇒ ∠A + ∠B + ∠C + ∠D = 360°
Using equation (1), (2), (3) and (4),
⇒ 3k + 2k + 3k + k = 360°
⇒ 9k = 360°
⇒ k =
⇒ k = 40°
Thus:
∠A = 3k = 3 x 40° = 120°
∠B = 2k = 2 x 40° = 80°
∠C = 3k = 3 x 40° = 120°
∠D = k = 40°
Hence, the angles of the quadrilateral are ∠A = 120°, ∠B = 80°, ∠C = 120° and ∠D = 40°.
The sum of interior angles of a regular polygon is thrice the sum of its exterior angles. Find the number of sides in the polygon.
Answer
It is given that the sum of the interior angles of a regular polygon is thrice the sum of its exterior angles.
Let the exterior angle of the polygon be a.
Then the interior angle is 3a.
As we know, the sum of the interior angle and the exterior angle is 180°.
⇒ a + 3a = 180°
⇒ 4a = 180°
⇒ a =
⇒ a = 45°
So, the exterior angle is 45°.
The interior angle is 3a = 3 x 45° = 135°.
Each interior angle of a regular polygon can be calculated using the formula:
⇒ 135° =
By cross multiplying, we get
⇒ 135°n = (2n - 4) 90°
⇒ 135°n = 180°n - 360°
⇒ 180°n - 135°n = 360°
⇒ 45°n = 360°
⇒ n =
⇒ n = 8
Hence, the number of sides is 8.
Angles of a quadrilateral are (4x)°, 5(x + 2)°, (7x - 20)° and 6(x + 3)°. Find:
(i) the value of x.
(ii) each angle of the quadrilateral.
Answer
(i) It is given that the angles of a quadrilateral are (4x)°, 5(x + 2)°, (7x - 20)° and 6(x + 3)°.
As we know, the sum of all angles in a quadrilateral is 360°.
So,
⇒ ∠A + ∠B + ∠C + ∠D = 360°
⇒ (4x)° + 5(x + 2)° + (7x - 20)° + 6(x + 3)° = 360°
⇒ 4x° + 5x° + 10° + 7x° - 20° + 6x° + 18° = 360°
⇒ 22x° + 8° = 360°
⇒ 22x° = 360° - 8°
⇒ 22x° = 352°
⇒ x° =
⇒ x° = 16°
Hence, the value of x is 16.
(ii) Each angle is (4x)°, 5(x + 2)°, (7x - 20)° and 6(x + 3)°:
= (4 16)°, 5(16 + 2)°, (7 16 - 20)° and 6(16 + 3)°
= 64°, 5(18)°, (122 - 20)° and 6(19)°
= 64°, 90°, 92° and 114°
Hence, the angles of the quadrilateral are 64°, 90°, 92° and 114°.
Use the information given in the following figure to find:
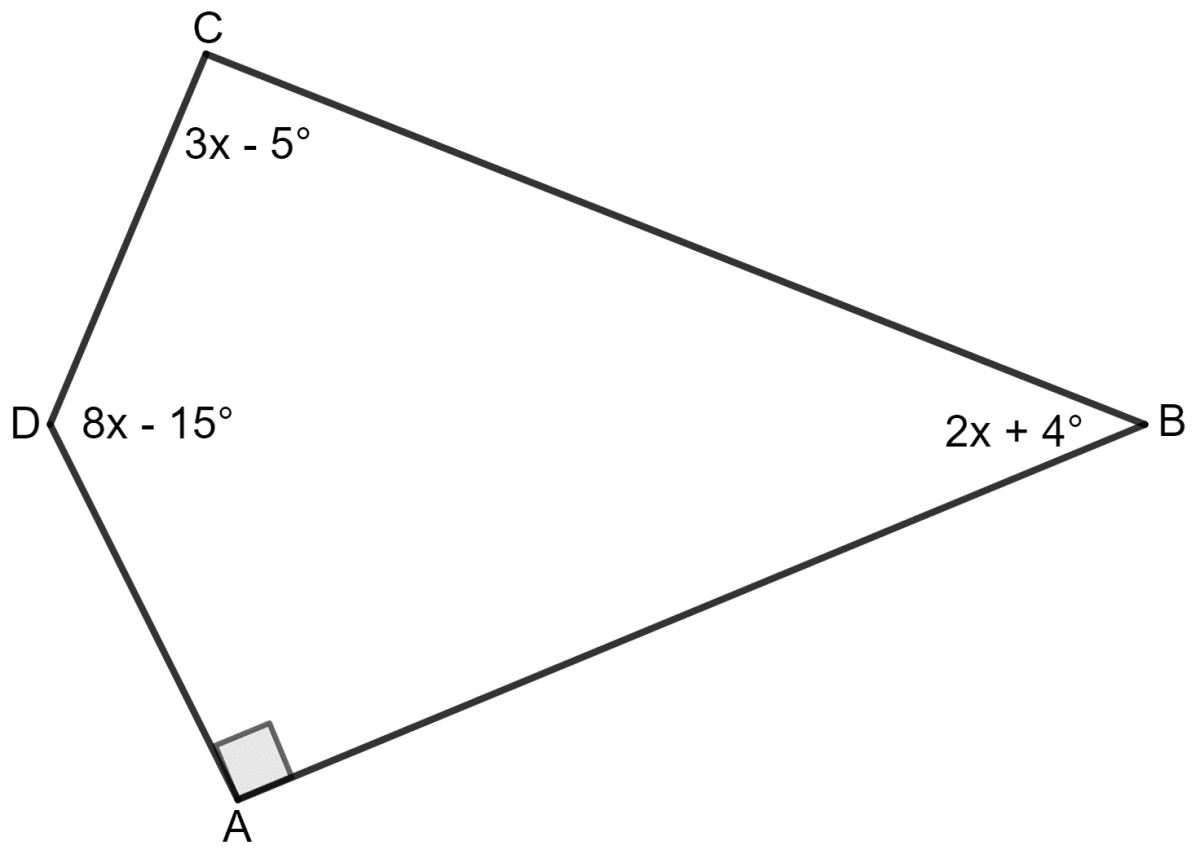
(i) x.
(ii) ∠B and ∠C.
Answer
(i) It is given that the angles of a quadrilateral are (3x - 5)°, (8x - 15)°, (2x + 4)° and 90°.
As we know, the sum of all angles in a quadrilateral is 360°.
So,
⇒ ∠A + ∠B + ∠C + ∠D = 360°
⇒ 90° + (2x + 4)° + (3x - 5)° + (8x - 15)° = 360°
⇒ 90° + 2x° + 4° + 3x° - 5° + 8x° - 15° = 360°
⇒ 74° + 13x° = 360°
⇒ 13x° = 360° - 74°
⇒ 13x° = 286°
⇒ x° =
⇒ x° = 22°
Hence, the value of x is 22.
(ii) ∠B = (2x + 4)°
= (2 22 + 4)°
= (44 + 4)°
= 48°
∠C = (3x - 5)°
= (3 22 - 5)°
= (66 - 5)°
= 61°
Hence, ∠B = 48° and ∠C = 61°.