Find the coordinates of points whose
(i) abscissa is 3 and ordinate -4.
(ii) abscissa is and ordinate 5.
(iii) whose abscissa is and ordinate .
(iv) whose ordinate is 5 and abscissa is -2.
(v) whose abscissa is -2 and lies on x-axis.
(vi) whose ordinate is and lies on y-axis.
Answer
We know that,
Abscissa is the x-coordinate and ordinate is the y-coordinate of a point.
(i) The coordinate of the point whose abscissa is 3 and ordinate is -4 is (3, -4).
(ii) The coordinate of the point whose abscissa is and ordinate is 5 is .
(iii) The coordinate of the point whose whose abscissa is and ordinate is .
(iv) The coordinate of the point whose ordinate is 5 and abscissa is -2 is (-2, 5).
(v) Since, point lies on x-axis. So, ordinate of point will be = 0.
The coordinate of the point whose abscissa is -2 and lies on x-axis is (-2,0).
(vi) Since, point lies on y-axis. So, abscissa of point will be = 0.
The coordinate of the point whose ordinate is and lies on y-axis is .
In which quadrant or on which axis each of the following points lie?
(-3, 5), (4, -1) (2, 0), (2, 2), (-3, -6)
Answer
From figure,

(-3, 5) lies in second quadrant.
(4, -1) lies in fourth quadrant.
(2, 0) lies on x-axis.
(2, 2) lies in first quadrant.
(-3, -6) lies in third quadrant.
Which of the following points lie on (i) x-axis? (ii) y-axis?
A(0, 2), B(5, 6), C(23, 0), D(0, 23), E(0, -4), F(-6, 0), G (,0).
Answer
Given points are A (0, 2), B (5, 6), C (23, 0), D (0, 23), E (0, -4), F (-6, 0), G (,0)
(i) If y-coordinate of a point is zero, then the point lies on x-axis.
Hence, C(23, 0), F(-6, 0) and G(, 0) lies on x-axis.
(ii) If x-coordinate of a point is zero, then the point lies on y-axis.
Hence, A(0, 2), D(0, 23) and E(0, -4) lies on y-axis.
Plot the following points on the graph paper :
A(3, 4), B(-3, 1), C(1, -2), D(-2, -3), E(0, 5), F(5, 0), G(0, -3), H(-3, 0).
Answer
The points are shown in the below graph:

Write the co-ordinates of the points A, B, C, D, E, F, G and H shown in the adjacent figure.

Answer
From figure,
The co-ordinates of the points are:
| Point | Co-ordinates |
|---|---|
| A | (2, 2) |
| B | (-3, 0) |
| C | (-2, -4) |
| D | (3, -1) |
| E | (-4, 4) |
| F | (0, -2) |
| G | (2, -3) |
| H | (0, 3) |
In which quadrants are the points A, B, C and D of problem 5 located ?
Answer
In point A(2, 2), both x and y coordinates are positive. So it lies in the first quadrant.
In point B(-3, 0), y-coordinate is zero. So it lies on x-axis.
In point C(-2, -4), both x and y coordinates are negative. So it lies in the third quadrant.
In point D(3, -1), x coordinate is positive and y coordinate is negative. So it lies in the fourth quadrant.
Plot the following points on the same graph paper :
Answer
The points are shown on the graph below:

Plot the following points on the same graph paper.
Answer
The points are shown on the graph below:

Plot the following points and check whether they are collinear or not :
(i) (1, 3), (-1, -1) and (-2, -3)
(ii) (1, 2), (2, -1) and (-1, 4)
(iii) (0, 1), (2, -2) and .
Answer
(i)

Points (1, 3), (-1, -1) and (-2, -3) lie on a straight line, so they are collinear.
(ii)

Points (1, 2), (2, -1) and (-1, 4) do not lie on a line. So they are non-collinear.
(iii)

Points (0, 1), (2, -2) and lie on a straight line, so they are collinear.
Plot the point P(-3, 4). Draw PM and PN perpendiculars to x-axis and y-axis respectively. State the co-ordinates of the points M and N.
Answer
The points are shown on the graph below:

Steps of construction :
Plot point P(-3, 4) on graph.
Draw PM and PN which are perpendiculars to x-axis and y-axis respectively.
From figure,
Coordinates of point M = (-3, 0) and N = (0, 4).
Plot the points A(1, 2), B(-4, 2), C(-4, -1) and D (1, -1). What kind of quadrilateral is ABCD? Also find the area of the quadrilateral ABCD.
Answer
The points are shown on the graph below:

Steps of construction :
Plot the points A (1, 2), B (-4, 2), C (-4, -1) and D (1, -1) on graph.
Join AB, BC, CD and AD.
From graph,
ABCD is a rectangle.
1 block = 1 unit
AB = 5 units, AD = 3 units
Area of rectangle ABCD = length × breadth
= AB × AD
= 5 × 3
= 15 sq. units.
Hence, ABCD is a rectangle and its area = 15 sq. units.
Plot the points (0, 2), (3, 0), (0, -2) and (-3, 0) on a graph paper. Join these points (in order). Name the figure so obtained and find the area of the figure obtained.
Answer
The points are shown on the graph below:

Steps of construction :
Plot the points A(0, 2), B(3, 0), C(0, -2) and D(-3,0) on graph.
Join AB, BC, CD and DA. ABCD is a rhombus.
Join BD and AC.
BD and AC are the diagonals of the rhombus.
Area of a rhombus = × d1 × d2
From graph,
1 block = 1 unit.
AC = 4 units
BD = 6 units.
Area of rhombus ABCD = × BD × AC
= × 6 × 4
= 12 sq. units.
Hence, figure obtained form graph is a rhombus with area = 12 sq. units.
Three vertices of a square are A(2, 3), B (-3, 3) and C (-3, -2). Plot these points on a graph paper and hence use it to find the co-ordinates of the fourth vertex. Also find the area of the square.
Answer
The points are shown on the graph below:

Steps of construction :
Plot points A(2, 3), B(-3, 3) and C(-3, -2) on graph.
Measure AB.
Mark point D such that it is at a distance AB from points A and C.
Join AB, BC, CD and DA.
On measuring,
AB = 5 units [As, 1 block = 1 unit]
Area of the square = side × side
Area of the square ABCD = AB × AB
= 5 × 5 = 25 sq. units.
Hence, the coordinates of D = (2, -2) and area of the square is 25 sq. units.
Write the co-ordinates of the vertices of a rectangle which is 6 units long and 4 units wide if the rectangle is in the first quadrant, its longer side lies on the x-axis and one vertex is at the origin.
Answer
The points are shown on the graph below:

Given,
The rectangle which is 6 units long and 4 units wide is shown in the graph.
Rectangle is in the first quadrant.
Longer side lies on x-axis and one vertex is at origin A(0, 0).
Steps of construction :
Mark point A(0, 0).
At a distance of 6 units on x-axis mark point B(6, 0).
From B draw a line segment parallel to y-axis and mark point C on it at distance of 4 units.
From C draw a line segment parallel to x-axis and mark point D on it at distance of 6 units.
Join DA.
Hence, coordinates of the rectangle are A(0, 0), B(6, 0), C(6, 4) and D(0, 4).
In the adjoining figure, ABCD is a rectangle with length 6 units and breadth 3 units. If O is the mid-point of AB, find the coordinates of A, B, C and D.

Answer
Given,
Length = 6 units.
Breadth = 3 units
AB = 6 units.
As, 1 block = 1 unit
From graph,

A = (-3, 0)
B = (3, 0)
C = (3, 3)
D = (-3, 3).
The adjoining figure shows an equilateral triangle OAB with each side = 2a units. Find the coordinates of the vertices.
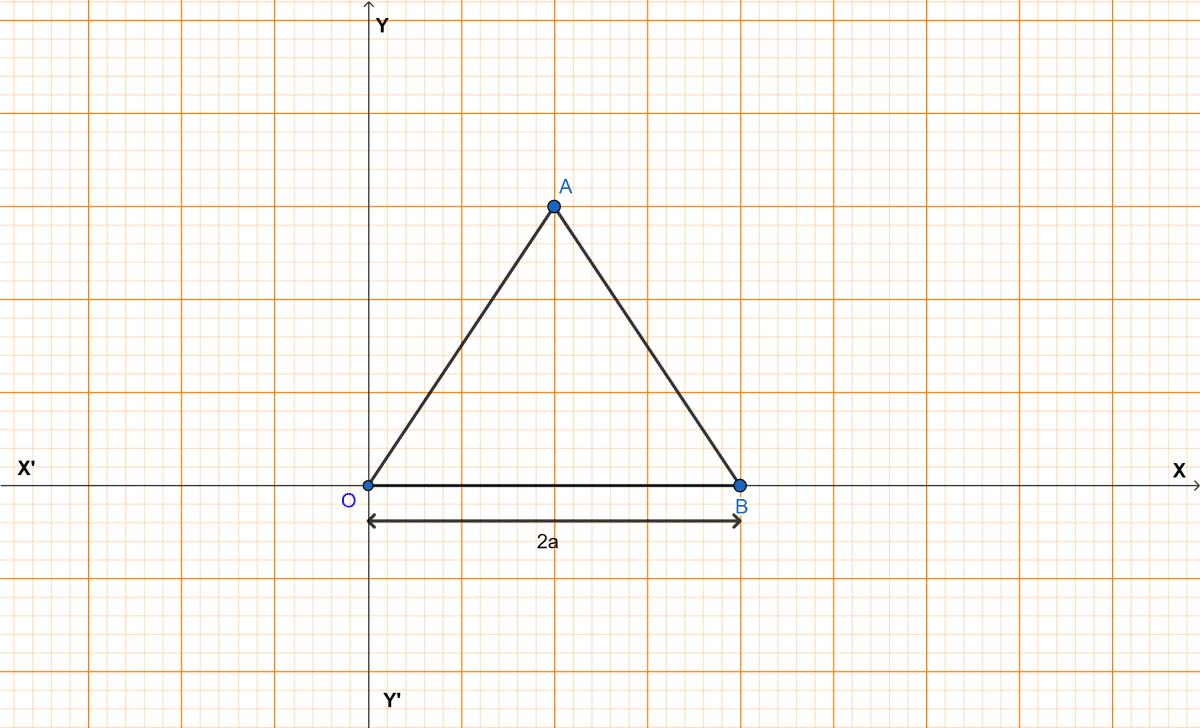
Answer
Given equilateral triangle OAB.
OA = OB = AB = 2a units.
Draw AD ⊥ OB.
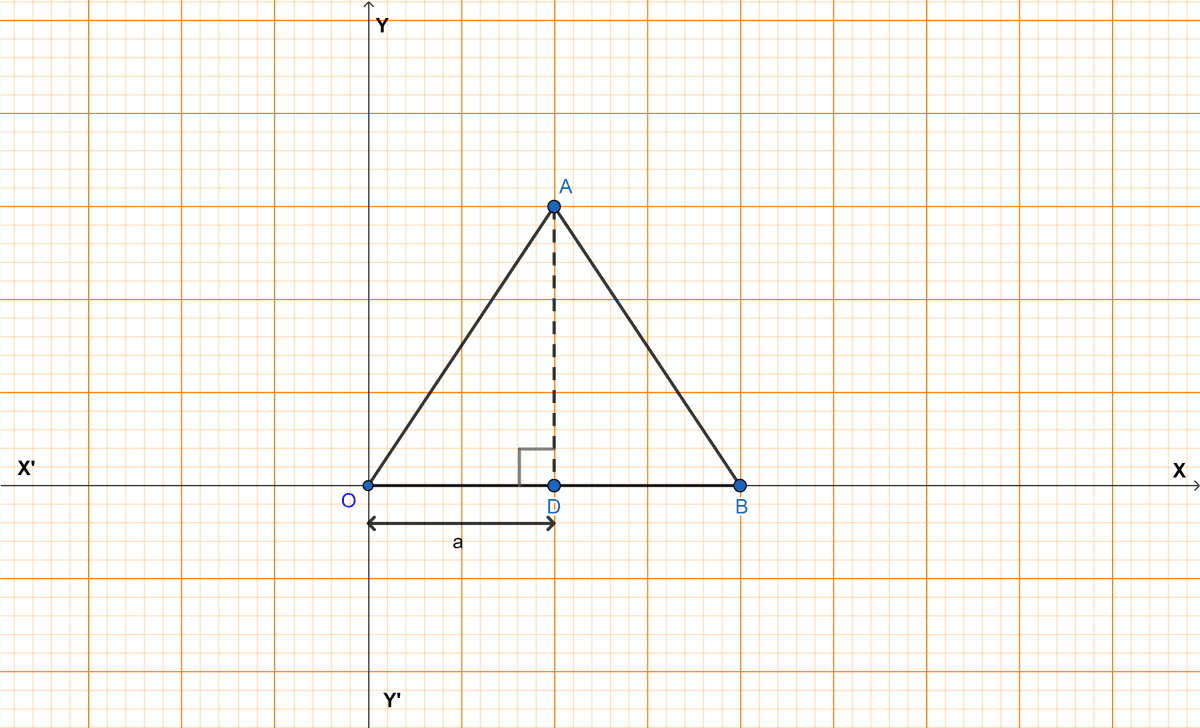
In an equilateral triangle, a perpendicular drawn from one of the vertices to the opposite side bisects the side.
∴ OD = x OB = x 2a = a.
In right angle triangle OAD,
⇒ OA2 = OD2 + AD2
⇒ (2a)2 = a2 + AD2
⇒ 4a2 = a2 + AD2
⇒ AD2 = 4a2 - a2
⇒ AD2 = 3a2
⇒ AD = units.
⇒ AD = a units.
From graph,
Co-ordinates of O = (0, 0)
Co-ordinates of B = (2a, 0)
As, OD = a units and AD = a units.
Co-ordinates of A = (a, a).
Hence, co-ordinates of O = (0, 0), B = (2a, 0) and A = (a, a).
In the given figure, △PQR is equilateral. If the coordinates of the points Q and R are (0, 2) and (0, -2) respectively, find the coordinates of the point P.
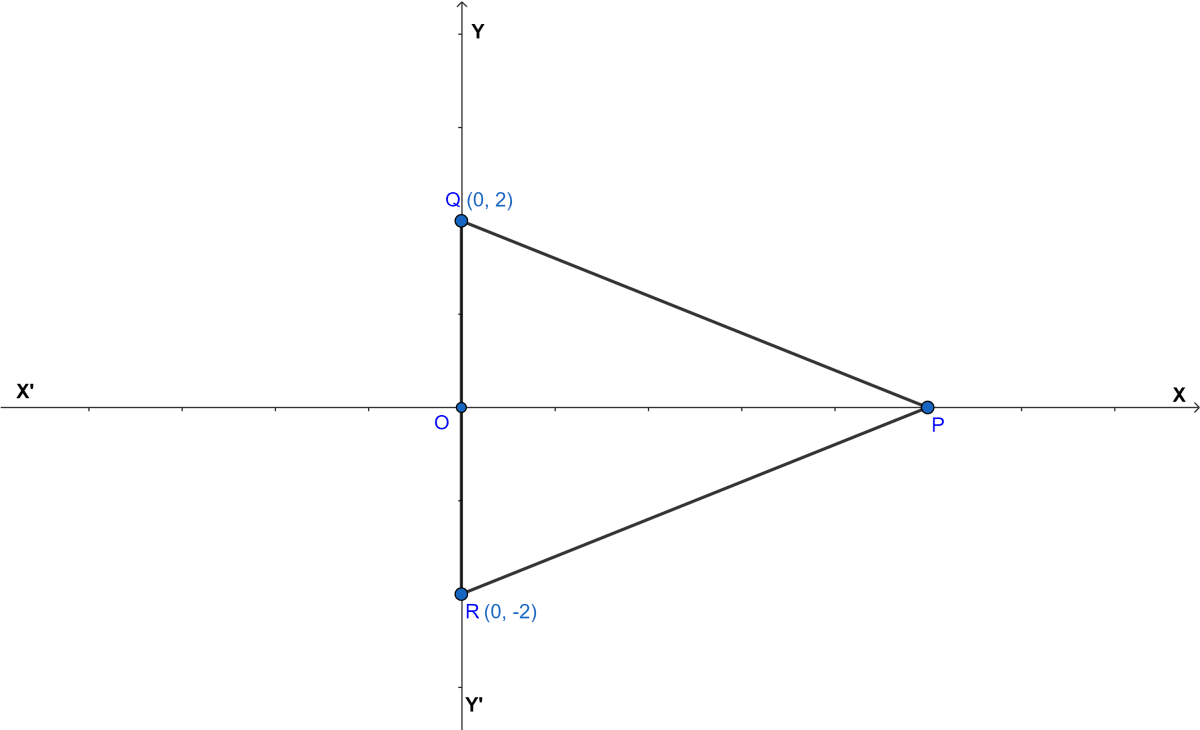
Answer
Given, PQR is an equilateral triangle in which Q(0, 2) and R(0, -2) and O = (0, 0).
Let (x, 0) be the coordinates of P. [As, P lies on x axis, so y-coordinate is zero.]
By distance formula,
PQ = PR = QR = 4.
OQ = 2
In right angle triangle POQ,
⇒ PQ2 = OP2 + OQ2 [By pythagoras theorem]
⇒ 42 = OP2 + 22
⇒ 16 = OP2 + 4
⇒ OP2 = 16 - 4
⇒ OP2 = 12
⇒ OP = .
Since, P lies on x-axis and OP = .
Hence, the coordinates of P are (, 0).
Draw the graph of the following linear equation :
2x + y + 3 = 0
Answer
The given equation 2x + y + 3 = 0, can be written as :
⇒ y = -2x - 3
When x = 0, y = -2(0) - 3 = -3,
x = 1, y = -2(1) - 3 = -2 - 3 = -5,
x = 2, y = -2(2) - 3 = -4 - 3 = -7.
Table of values :
| x | y |
|---|---|
| 0 | -3 |
| 1 | -5 |
| 2 | -7 |
Steps of construction :
Plot the points (0, -3), (1, -5) and (2, -7) on the graph.
Connect any two points by a straight line.
Observe that the third point lies on the straight line.

Hence, the graph of the given equation is shown in the adjoining figure.
Draw the graph of the following linear equation :
x - 5y - 4 = 0
Answer
The given equation x - 5y - 4 = 0, can be written as :
⇒ 5y = x - 4
⇒ y = (x - 4)
When x = -6, y = = -2,
x = -1, y = = -1,
x = 4, y = = 0.
Table of values :
| x | y |
|---|---|
| -6 | -2 |
| -1 | -1 |
| 4 | 0 |
Steps of construction :
Plot the points (-6, -2), (-1, -1) and (4, 0) on the graph.
Connect any two points by a straight line.
Observe that the third point lies on the straight line.

Hence, the graph of the given equation is shown in the adjoining figure.
Draw the graph of 3y = 12 - 2x. Take 2 cm = 1 unit on both axes.
Answer
The above equation, 3y = 12 - 2x can be written as :
⇒ 3y = 12 - 2x
⇒ y =
⇒ y = 4 - .
When x = -3, y = 4 - = 4 - (-2) = 6,
x = 0, y = 4 - = 4,
x = 3, y = 4 - = 4 - 2 = 2.
Table of values :
| x | y |
|---|---|
| -3 | 6 |
| 0 | 4 |
| 3 | 2 |
Steps of construction :
Plot the points (-3, 6), (0, 4) and (3, 2) on the graph.
Connect any two points by a straight line.
Observe that the third point lies on the straight line.

Hence, the graph of the given equation is shown in the adjoining figure.
Draw the graph of 5x + 6y - 30 = 0 and use it to find the area of the triangle formed by the line and coordinate axes.
Answer
The above equation, 5x + 6y - 30 = 0 can be written as :
⇒ 6y = -5x + 30
⇒ y =
⇒ y = .
When x = 0, y = - = 0 + 5 = 5,
x = 6, y = - = -5 + 5 = 0,
x = 12, y = - + 5 = -10 + 5 = -5.
Table of values :
| x | y |
|---|---|
| 0 | 5 |
| 6 | 0 |
| 12 | -5 |
Steps of construction :
Plot the points (0, 5), (6, 0) and (12, -5) on the graph.
Connect any two points by a straight line.
Observe that the third point lies on the straight line.
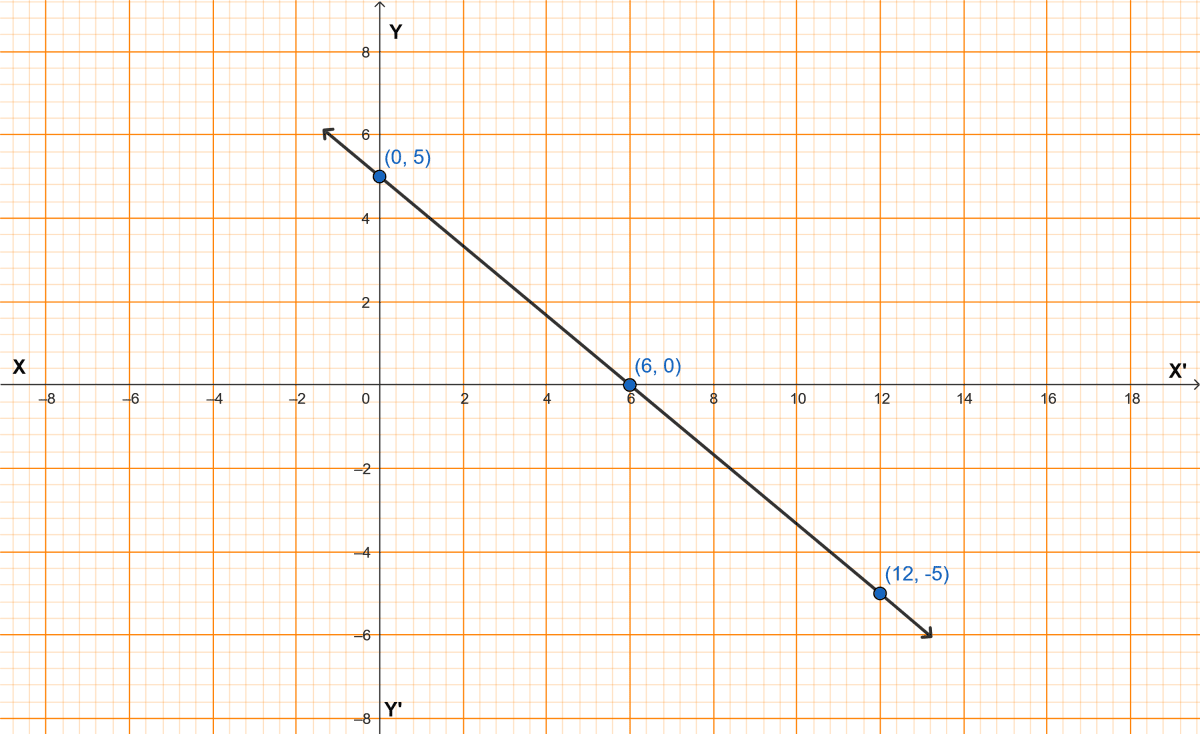
By formula,
Area of triangle =
From graph,
Base = 6 units, Height = 5 units.
Area = sq. units.
Hence, the graph of the given equation is shown in the adjoining figure and area of triangle = 15 sq. units.
Draw the graph of 4x - 3y + 12 = 0 and use it to find the area of the triangle formed by the line and co-ordinate axes. Take 2 cm = 1 unit on both axes.
Answer
The above equation, 4x - 3y + 12 = 0 can be written as :
⇒ 3y = 4x + 12
⇒ y =
When x = -6, y = = -8 + 4 = -4,
x = -3, y = -4 + 4 = 0,
x = 0, y = 0 + 4 = 4.
Table of values :
| x | y |
|---|---|
| -6 | -4 |
| -3 | 0 |
| 0 | 4 |
Steps of construction :
Plot the points (-6, -4), (-3, 0) and (0, 4) on the graph.
Connect any two points by a straight line.
Observe that the third point lies on the straight line.
By formula,
Area of triangle =
From graph,
Base = 3 units, Height = 4 units.
Area = sq. units.
Hence, the graph of the given equation is shown in the adjoining figure and area of triangle = 6 sq. units.
Draw the graph of the equation y = 3x - 4. Find graphically
(i) the value of y when x = -1
(ii) the value of x when y = 5.
Answer
Equation :
⇒ y = 3x - 4
When x = 0, y = 3(0) - 4 = 0 - 4 = -4,
x = 2, y = 3(2) - 4 = 6 - 4 = 2,
Table of values :
| x | y |
|---|---|
| 0 | -4 |
| 2 | 2 |
Steps of construction :
Plot the points (0, -4) and (2, 2) on the graph.
Connect the two points by a straight line.
Hence, the graph of the given equation is shown in the adjoining figure.
(i) Steps of construction :
From point, P (x = -1) draw a line parallel to y-axis touching the graph. Mark the point as Q.
From Q draw a line parallel to x-axis, touching y-axis at point R (y = -7).
Hence, y = -7, when x = -1.
(ii) Steps of construction :
From point, S (y = 5) draw a line parallel to x-axis touching the graph. Mark the point as T.
From T draw a line parallel to y-axis, touching x-axis at point U (x = 3).

Hence, x = 3, when y = 5.
The graph of a linear equation in x and y passes through (4, 0) and (0, 3). Find the value of k if the graph passes through (k, 1.5).
Answer
Steps of construction :
Plot the points (4, 0) and (0, 3) on graph.
Connect the points through a straight line.
Take a point Q (y = 1.5) and draw a line parallel to x-axis touching the graph at point R.
From point R draw a line parallel to y-axis and touching x-axis at point S (x = 2).

From graph R = (2, 1.5)
Comparing point R with (k, 1.5), we get :
k = 2.
Hence, the value of k = 2.
Use the table given alongside to draw the graph of a straight line. Find, graphically, the values of a and b.
| x | 1 | 2 | 3 | a |
|---|---|---|---|---|
| y | -2 | b | 4 | -5 |
Answer
Steps of construction :
Plot the points (1, -2) and (3, 4) on graph paper.
Connect the points through a straight line.
Take a point C (x = 2) and draw a line parallel to y-axis touching the graph at point B.
From point B draw a line parallel to x-axis and touching y-axis at point A (y = 1).

From graph,
B = (2, 1)
Comparing it with (2, b) we get :
b = 1.
Also, the graph touches y-axis at (0, -5).
Comparing it with (a, -5) we get :
a = 0.
Hence, a = 0 and b = 1.
Solve the following equations graphically :
3x - 2y = 4, 5x - 2y = 0.
Answer
Given,
Equation :
⇒ 3x - 2y = 4
⇒ 2y = 3x - 4
⇒ y = x - 2 .........(1)
When, x = -2, y = = -3 - 2 = -5,
x = 0, y = = 0 - 2 = -2,
x = 2, y = = 3 - 2 = 1.
Tables of values for equation (1)
| x | -2 | 0 | 2 |
|---|---|---|---|
| y | -5 | -2 | 1 |
Steps of construction :
Plot the points (-2, -5), (0, -2) and (2, 1) on graph paper.
Connect points by straight line.
Given,
Equation :
⇒ 5x - 2y = 0
⇒ 2y = 5x
⇒ y = ..............(2)
When, x = -2, y = = -5,
x = 0, y = = 0,
x = 2, y = = 5.
Tables of values for equation (2)
| x | -2 | 0 | 2 |
|---|---|---|---|
| y | -5 | 0 | 5 |
Steps of construction :
Plot the points (-2, -5), (0, 0) and (2, 5) on graph paper.
Connect points by straight line.
The graphs of both the straight lines are shown in the figure.

The lines intersect at point A(-2, -5).
Hence, the solution of the given equations is x = -2, y = -5.
Solve the following pair of equations graphically. Plot atleast 3 points for each straight line.
2x - 7y = 6, 5x - 8y = -4.
Answer
Given,
Equation :
⇒ 2x - 7y = 6
⇒ 2x = 6 + 7y
⇒ x = ..........(1)
When y = 0, x = = 3,
y = -1, x = = -0.5,
y = -2, x = = -4.
Table of values for equation (1)
| x | 3 | -0.5 | -4 |
|---|---|---|---|
| y | 0 | -1 | -2 |
Steps of construction :
Plot the points (3, 0), and (-4, -2) on graph paper.
Connect points by straight line.
Given,
Equation :
⇒ 5x - 8y = -4
⇒ 5x = 8y - 4
⇒ x = y - ..............(2)
When, y = 0, x = -0.8,
y = 3, x = = 4,
y = -2, x = = -4.
Table of values for equation (2)
| x | -0.8 | 4 | -4 |
|---|---|---|---|
| y | 0 | 3 | -2 |
Steps of construction :
Plot the points (-0.8, 0), (4, 3) and (-4, -2) on graph paper.
Connect points by straight line.
The graphs of both the straight lines are shown in the figure.
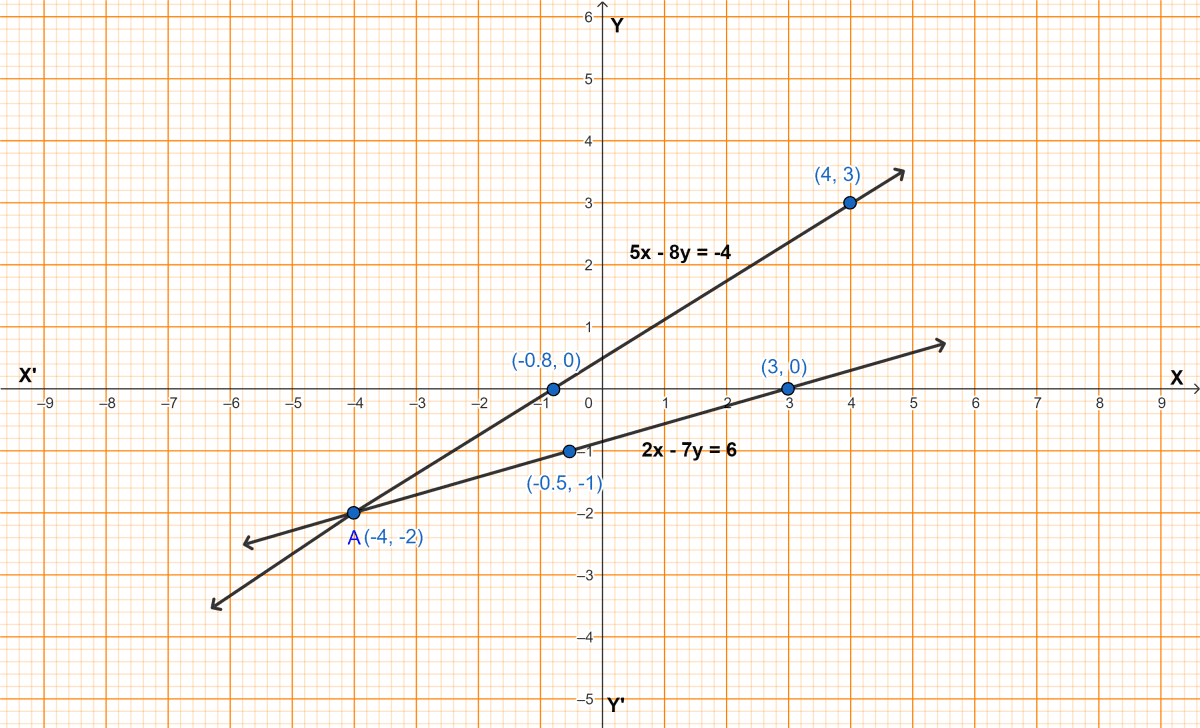
The lines intersect at point A(-4, -2).
Hence, the solution of the given equations is x = -4, y = -2.
Using the same axes of coordinates and the same unit, solve graphically.
x + y = 0, 3x - 2y = 10.
Answer
Given,
Equation :
⇒ x + y = 0
⇒ y = -x .............(1)
When, x = 0, y = 0,
x = 1, y = -(1) = -1,
x = 2, y = -(2) = -2.
Table of values for equation (1)
| x | 0 | 1 | 2 |
|---|---|---|---|
| y | 0 | -1 | -2 |
Steps of construction :
Plot the points (0, 0), (1, -1) and (2, -2) on graph paper.
Connect points by straight line.
Given,
Equation :
⇒ 3x - 2y = 10
⇒ 2y = 3x - 10
⇒ y = ............(2)
When, x = 0, y = = 0 - 5 = -5,
x = 2, = 3 - 5 = -2,
x = 4, = 6 - 5 = 1.
Table of values for equation (2)
| x | 0 | 2 | 4 |
|---|---|---|---|
| y | -5 | -2 | 1 |
Steps of construction :
Plot the points (0, -5), (2, -2) and (4, 1) on graph paper.
Connect points by straight line.
The graphs of both the straight lines are shown in the figure.

The lines intersect at point A(2, -2).
Hence, the solution of the given equations is x = 2, y = -2.
Take 1 cm to represent 1 unit on each axis to draw the graphs of the equations 4x - 5y = -4 and 3x = 2y - 3 on the same graph sheet (same axes). Use your graph to find the solution of the above simultaneous equations.
Answer
Given,
Equation :
⇒ 4x - 5y = -4
⇒ 5y = 4x + 4
⇒ y = .............(1)
When, x = -1, y = = 0,
x = 1.5, y = = 2,
x = 4, y = = 4.
Table of values for equation (1)
| x | -1 | 1.5 | 4 |
|---|---|---|---|
| y | 0 | 2 | 4 |
Steps of construction :
Plot the points (-1, 0), (1.5, 2) and (4, 4) on graph paper.
Connect points by straight line.
Given,
Equation :
⇒ 3x = 2y - 3
⇒ 2y = 3x + 3
⇒ y = ............(2)
When, x = -1, y = = 0,
x = 0, = 1.5,
x = 1, = 3.
Table of values for equation (2)
| x | -1 | 0 | 1 |
|---|---|---|---|
| y | 0 | 1.5 | 3 |
Steps of construction :
Plot the points (-1, 0), (0, 1.5) and (1, 3) on graph paper.
Connect points by straight line.
The graphs of both the straight lines are shown in the figure.
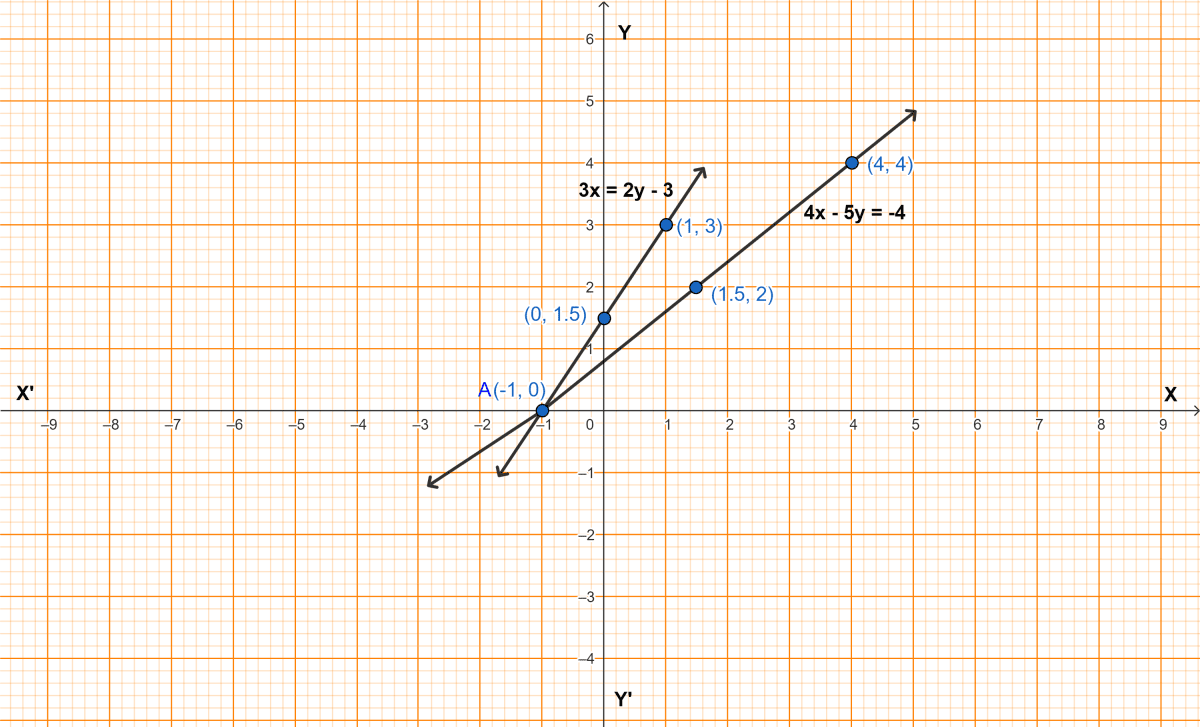
The lines intersect at point A(-1, 0).
Hence, the solution of the given equations is x = -1, y = 0.
Solve the following simultaneous equations graphically :
x + 3y = 8, 3x = 2 + 2y.
Answer
Given,
Equation :
x + 3y = 8
x = 8 - 3y ..........(1)
When, y = 1, x = 8 - 3(1) = 8 - 3 = 5,
y = 2, x = 8 - 3(2) = 8 - 6 = 2,
y = 3, x = 8 - 3(3) = 8 - 9 = -1.
Table of values for equation (1)
| x | -1 | 2 | 5 |
|---|---|---|---|
| y | 3 | 2 | 1 |
Steps of construction :
Plot the points (-1, 3), (2, 2) and (5, 1) on graph paper.
Connect points by straight line.
Given,
Equation :
⇒ 3x = 2 + 2y
⇒ x = ..........(2)
When, y = -1, x = = 0.
y = 2, x = = 2,
y = 5, x = = 4.
Table of values for equation (2)
| x | 0 | 2 | 4 |
|---|---|---|---|
| y | -1 | 2 | 5 |
Steps of construction :
Plot the points (0, -1), (2, 2) and (4, 5) on graph paper.
Connect points by straight line.
The graphs of both the straight lines are shown in the figure.

The lines intersect at point A(2, 2).
Hence, the solution of the given equations is x = 2, y = 2..
Solve graphically the simultaneous equations 3y = 5 - x, 2x = y + 3.
Answer
Given,
⇒ 3y = 5 - x
⇒ y = .......(1)
When x = -4, y = = 3,
x = -1, y = = 2,
x = 2, y = = 1.
Table of values for equation (1)
| x | -4 | -1 | 2 |
|---|---|---|---|
| y | 3 | 2 | 1 |
Steps of construction :
Plot the points (-4, 3), (-1, 2) and (2, 1) on graph paper.
Connect points by straight line.
Given,
⇒ 2x = y + 3
⇒ y = 2x - 3 ...........(2)
When x = 0, y = 2 × 0 - 3 = 0 - 3 = -3,
x = 1, y = 2 × 1 - 3 = 2 - 3 = -1,
x = 2, y = 2 × 2 - 3 = 4 - 3 = 1.
Table of values for equation (2)
| x | 0 | 1 | 2 |
|---|---|---|---|
| y | -3 | -1 | 1 |
Steps of construction :
Plot the points (0, -3), (1, -1) and (2, 1) on graph paper.
Connect points by straight line.
From graph,

The two lines meet at point P(2, 1).
Hence, the solution of the given equations is x = 2, y = 1.
Use graph paper for this question. Take 2 cm = 1 unit on both axes.
(i) Draw the graphs of x + y + 3 = 0 and 3x - 2y + 4 = 0. Plot three points per line.
(ii) Write down the coordinates of the point of intersection of the lines.
(iii) Measure and record the distance of the point of intersection of the lines from the origin in cm.
Answer
(i) Given,
⇒ x + y + 3 = 0
⇒ y = -(3 + x) .........(1)
When x = -1, y = -[3 + (-1)] = -(3 - 1) = -2,
x = 0, y = -(3 + 0) = -3,
x = 1, y = -(3 + 1) = -4.
Table of values for equation (1)
| x | -1 | 0 | 1 |
|---|---|---|---|
| y | -2 | -3 | -4 |
Steps of construction :
Plot the points (-1, -2), (0, -3) and (1, -4) on graph paper.
Connect points by straight line.
Given,
⇒ 3x - 2y + 4 = 0
⇒ 2y = 3x + 4
⇒ y =
When x = -2, y = = -1,
x = 0, y = = 2,
x = 2, y = = 5.
Table of values for equation (2)
| x | -2 | 0 | 2 |
|---|---|---|---|
| y | -1 | 2 | 5 |
Steps of construction :
Plot the points (-2, -1), (0, 2) and (2, 5) on graph paper.
Connect points by straight line.

(ii) From graph,
P(-2, -1) is the intersection of lines.
Hence, coordinates of point of intersection = (-2, -1).
(iii) From P, draw a perpendicular to y-axis.
As, 1 unit = 2 cm.
So, PQ = 2 unit = 4 cm, OQ = 1 unit = 2 cm.
In right angle triangle,
By pythagoras theorem,
⇒ OP2 = PQ2 + OQ2
⇒ OP2 = 42 + 22
⇒ OP2 = 16 + 4
⇒ OP2 = 20
⇒ OP = = 4.5 cm
Hence, distance of the point of intersection of the lines from the origin = 4.5 cm.
Solve the following simultaneous equations, graphically :
2x - 3y + 2 = 4x + 1 = 3x - y + 2.
Answer
Considering,
⇒ 2x - 3y + 2 = 4x + 1
⇒ 3y = 2x - 4x + 2 - 1
⇒ 3y = -2x + 1
⇒ y = .........(1)
When, x = -4, y = = 3,
x = -1, y = = 1,
x = 2, y = = -1.
Table of values for equation (1)
| x | -4 | -1 | 2 |
|---|---|---|---|
| y | 3 | 1 | -1 |
Steps of construction :
Plot the points (-4, 3), (-1, 1) and (2, -1) on graph paper.
Connect points by straight line.
Considering,
⇒ 4x + 1 = 3x - y + 2
⇒ y = 3x - 4x + 2 - 1
⇒ y = -x + 1
⇒ y = 1 - x ............(2)
When, x = 0, y = 1 - 0 = 1,
x = 1, y = 1 - 1 = 0,
x = 2, y = 1 - 2 = -1.
Table of values for equation (2)
| x | 0 | 1 | 2 |
|---|---|---|---|
| y | 1 | 0 | -1 |
Steps of construction :
Plot the points (0, 1), (1, 0) and (2, -1) on graph paper.
Connect points by straight line.

From graph,
The two lines intersect at P(2, -1).
Hence, the solution of the given equations is x = 2, y = -1.
Use graph paper for this question :
(i) Draw the graphs of 3x - y - 2 = 0 and 2x + y - 8 = 0. Take 1 cm = 1 unit on both axes and plot three points per line.
(ii) Write down the coordinates of the point of intersection and the area of the triangle formed by the lines and the x-axis.
Answer
(i) Given,
⇒ 3x - y - 2 = 0
⇒ y = 3x - 2 ............(1)
When x = 0, y = 3 × 0 - 2 = 0 - 2 = -2,
x = 1, y = 3 × 1 - 2 = 3 - 2 = 1,
x = 2, y = 3 × 2 - 2 = 6 - 2 = 4.
Table of values for equation (1)
| x | 0 | 1 | 2 |
|---|---|---|---|
| y | -2 | 1 | 4 |
Steps of construction :
Plot the points (0, -2), (1, 1) and (2, 4).
Join the points.
Given,
⇒ 2x + y - 8 = 0
⇒ y = 8 - 2x ...........(2)
When x = 2, y = 8 - 2 × 2 = 8 - 4 = 4,
x = 3, y = 8 - 2 × 3 = 8 - 6 = 2,
x = 4, y = 8 - 2 × 4 = 8 - 8 = 0.
Table of values for equation (2)
| x | 2 | 3 | 4 |
|---|---|---|---|
| y | 4 | 2 | 0 |
Steps of construction :
Plot the points (2, 4), (3, 2) and (4, 0).
Join the points.

(ii) From the graph,
P(2, 4) is the point of intersection of lines.
BC = cm
PV = 4 cm.
Area of triangle = × base × height
= × BC × PV
= × 4
= cm2.
Hence, P(2, 4) is the point of intersection of lines and area = cm2.
Solve the following system of linear equations graphically :
2x - y - 4 = 0, x + y + 1 = 0.
Hence, find the area of the triangle formed by these lines and the y-axis.
Answer
Given,
⇒ 2x - y - 4 = 0
⇒ y = 2x - 4 ............(1)
When x = 1, y = 2(1) - 4 = 2 - 4 = -2,
x = 2, y = 2(2) - 4 = 4 - 4 = 0,
x = 3, y = 2(3) - 4 = 6 - 4 = 2.
Table of values for equation (1)
| x | 1 | 2 | 3 |
|---|---|---|---|
| y | -2 | 0 | 2 |
Steps of construction :
Plot the points (1, -2), (2, 0) and (3, 2).
Join the points.
Given,
⇒ x + y + 1 = 0
⇒ y = -(x + 1) .............(2)
When, x = -1, y = -(-1 + 1) = 0,
x = 0, y = -(0 + 1) = -1,
x = 1, y = -(1 + 1) = -2.
Table of values for equation (2)
| x | -1 | 0 | 1 |
|---|---|---|---|
| y | 0 | -1 | -2 |
Steps of construction :
Plot the points (-1, 0), (0, -1) and (1, -2).
Join the points.
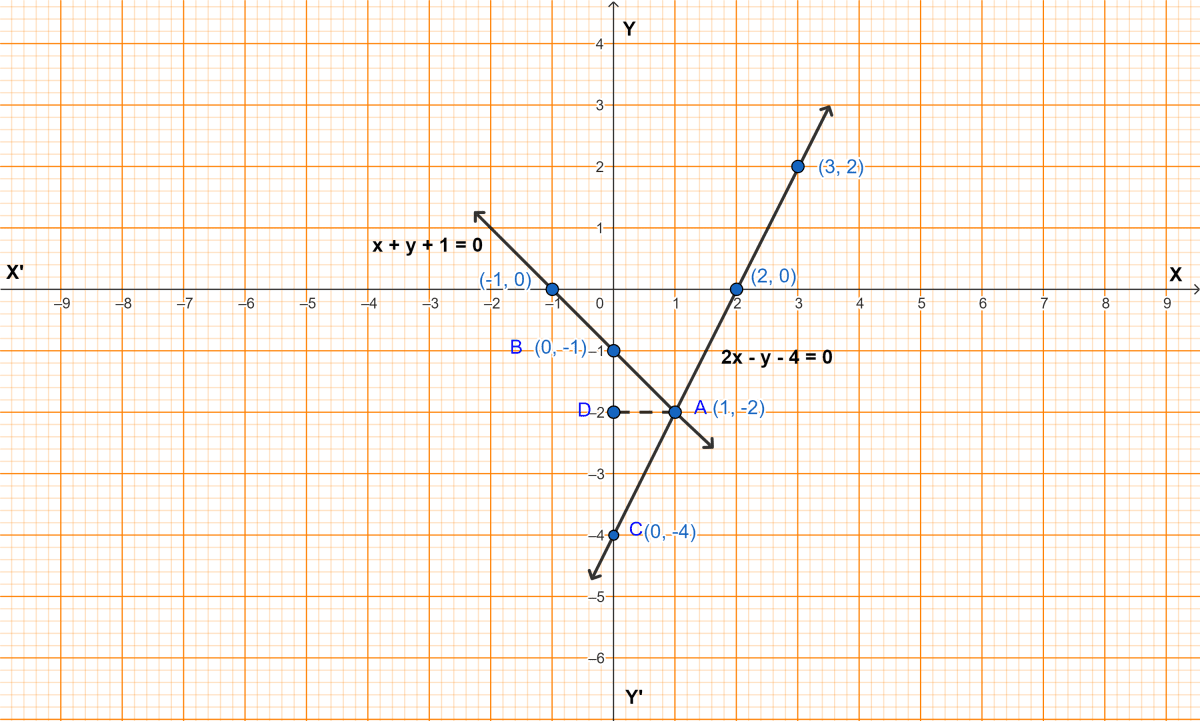
From graph,
A(1, -2) is the point of intersection of lines.
ABC are the vertices of triangle.
From A, draw AD perpendicular to BC.
AD = 1 unit and BC = 3 units.
Area of △ABC = × base × height
= × BC × AD
= × 3 × 1
= sq. units
Hence, point of intersection = (1, -2) and area of triangle = sq. units
Solve graphically the following equations: x + 2y = 4, 3x - 2y = 4.
Take 2 cm = 1 unit on each axis. Write down the area of the triangle formed by the lines and the y-axis. Also, find the area of the triangle formed by the lines and the x-axis.
Answer
Given,
⇒ x + 2y = 4
⇒ 2y = 4 - x
⇒ y = ......................(1)
When x = 0, y = = 2,
x = 2, y = = 1,
x = 4, y = = 0.
Table of values for equation (1)
| x | 0 | 2 | 4 |
|---|---|---|---|
| y | 2 | 1 | 0 |
Steps of construction :
Plot the points (0, 2), (2, 1) and (4, 0).
Join the points.
Given,
⇒ 3x - 2y = 4
⇒ 2y = 3x - 4
⇒ y = ..................(2)
When x = 0, y = = -2,
x = 2, y = = 1,
x = 4, y = = 4.
x = = 0.
Table of values for equation (2)
| x | 0 | 2 | 4 | |
|---|---|---|---|---|
| y | -2 | 1 | 4 | 0 |
Steps of construction :
Plot the points (0, -2), (2, 1), (4, 4) and .
Join the points.
From graph,
A(2, 1) is the point of intersection of lines.
AEF is the triangle between lines and y-axis.
From A, draw AG perpendicular to EF.
Using distance formula, distance =
Distance between E (0, 2) and F (0, -2)
= units
From graph,
AG = 2 units
EF = 4 units
Area of triangle = x base x height
= x EF x AG
= x 4 x 2
= 1 x 4
= 4 sq. units.
And, ABC is the triangle between lines and x-axis.
Using distance formula, distance =
Distance between B and C (4, 0)
=
From A, draw AD perpendicular to BC.
AD = 1 unit
BC = units
Area of triangle = x base x height
Hence, point of intersection of lines is x = 2, y = 1 and area of the triangle formed by the lines and the y-axis = 4 sq. unit and area of the triangle formed by the lines and the x-axis = sq units.
On graph paper, take 2 cm to represent one unit on both axes, draw the lines :
x + 3 = 0, y - 2 = 0, 2x + 3y = 12.
Write down the coordinates of the vertices of the triangle formed by these lines.
Answer
Given,
1st equation :
⇒ x + 3 = 0
⇒ x = -3 ............(1)
2nd equation :
⇒ y - 2 = 0
⇒ y = 2 .............(2)
3rd equation :
⇒ 2x + 3y = 12
⇒ 3y = 12 - 2x
⇒ y = .........(3)
When, x = -3, y = = 6,
x = 0, y = = 4,
x = 3, y = = 2.
Table of values of equation (3) :
| x | -3 | 0 | 3 |
|---|---|---|---|
| y | 6 | 4 | 2 |
Steps of construction :
Plot the points (-3, 6), (0, 4) and (3, 2).
Join the points.

From graph,
ABC is the required triangle.
Hence, coordinates of vertices of triangle formed by these lines = (-3, 6), (-3, 2) and (3, 2).
Find graphically the coordinates of the vertices of the triangle formed by the lines y = 0, y = x and 2x + 3y = 10. Hence, find the area of the triangle formed by these lines.
Answer
Given,
1st equation :
y = 0,
2nd equation :
y = x,
When, x = 0, y = 0,
x = 1, y = 1,
x = 2, y = 2.
Table of values of equation (2) :
| x | 0 | 1 | 2 |
|---|---|---|---|
| y | 0 | 1 | 2 |
Steps of construction :
Plot the points (0, 0), (1, 1) and (2, 2).
Join the points.
3rd equation :
⇒ 2x + 3y = 10
⇒ 3y = 10 - 2x
⇒ y = ..........(3)
When, x = -1, y = = 4,
x = 2, y = = 2,
x = 5, y = = 0.
Table of values of equation (3) :
| x | -1 | 2 | 5 |
|---|---|---|---|
| y | 4 | 2 | 0 |
Steps of construction :
Plot the points (-1, 4), (2, 2) and (5, 0).
Join the points.
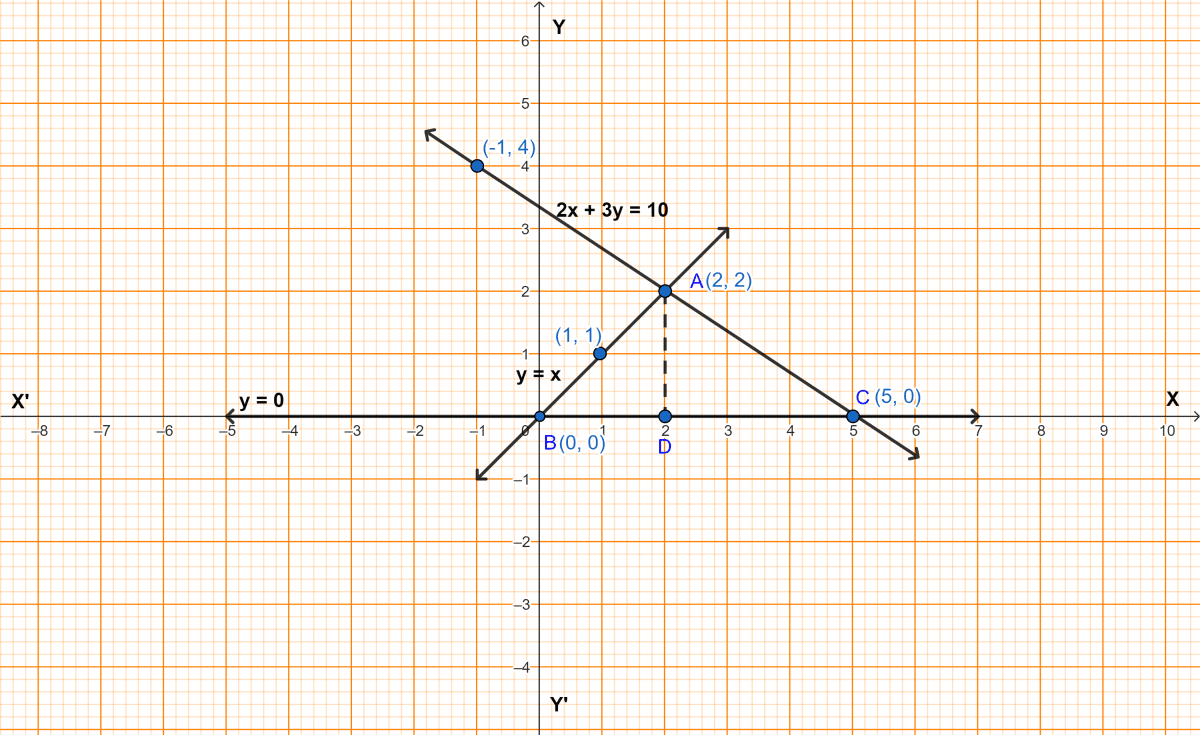
From graph,
ABC is the triangle.
From A, draw AD perpendicular to x-axis.
AD = 2 units and BC = 5 units.
Area of triangle = × base × height
=
=
= 5 sq. units.
Hence, coordinates of triangle are (0, 0), (5, 0) and (2, 2) and area = 5 sq. units.
Find the distance between the following pair of points :
(2, 3), (4, 1)
Answer
By distance formula,
d =
Let P(x1, y1) and Q(x2, y2) be the given points
Co-ordinates of P = (2, 3)
Co-ordinates of Q = (4, 1)
Hence, distance between (2, 3) and (4, 1) = units.
Find the distance between the following pair of points :
(0, 0), (36, 15)
Answer
By distance formula,
d =
Let P(x1, y1) and Q(x2, y2) be the given points
Co-ordinates of P = (0, 0)
Co-ordinates of Q = (36, 15)
Hence, distance between (0, 0) and (36, 15) = 39 units.
Find the distance between the following pair of points :
(a, b), (-a, -b)
Answer
By distance formula,
d =
Let P(x1, y1) and Q(x2, y2) be the given points
Co-ordinates of P = (a, b)
Co-ordinates of Q = (-a, -b)
Hence, distance between (a, b) and (-a, -b) = units.
A is a point on y-axis whose ordinate is 4 and B is a point on x-axis whose abscissa is -3. Find the length of the line segment AB.
Answer
Since, point A is on y-axis so its x-coordinate = 0.
Given,
Ordinate of A = 4.
∴ A = (0, 4).
Since, point B is on x-axis so its y-coordinate = 0.
Given,
Abscissa of B = -3.
∴ B = (-3, 0).
By distance formula,
Hence, AB = 5 units.
Find the value of a, if the distance between the points A (-3, -14) and B (a, -5) is 9 units.
Answer
By distance formula,
d =
On squaring both sides,
Hence, value of a = -3.
Find points on the x-axis which are at a distance of 5 units from the point (5, -4).
Answer
We know that,
y-coordinate of any point on x-axis = 0.
Let point on x-axis which is at a distance of 5 units from (5, -4) be P(x, 0).
By distance formula,
On squaring both sides,
∴ P = (x, 0) = (2, 0) or (8, 0).
Hence, points on the x-axis which are at a distance of 5 units from the point (5, -4) are (2, 0) or (8, 0).
Find points on the y-axis which are at a distance of 10 units from the point (8, 8).
Answer
We know that,
x-coordinate of any point on y-axis = 0.
Let point on y-axis which is at a distance of 10 units from (8, 8) be P(0, y).
By distance formula,
On squaring both sides,
∴ P = (0, y) = (0, 2) or (0, 14).
Hence, points on the y-axis which are at a distance of 10 units from the point (8, 8) are (0, 2) or (0, 14).
Find point (or points) which are at distance of units from the point (4, 3) given that the ordinate of the point (or points) is twice the abscissa.
Answer
Given,
Ordinate of the point is twice the abscissa.
Let abscissa of point be k, then ordinate = 2k
Let the required point be P.
∴ P = (k, 2k).
By distance formula,
d =
Given,
Distance between (4, 3) and (k, 2k) = units.
On squaring both sides
When k = 1,
P = (k, 2k) = (1, 2).
When k = 3,
P = (k, 2k) = (3, 6).
Hence, required points are (1, 2) or (3, 6).
Find the point on the x-axis which is equidistant from the points (2, -5) and (-2, 9).
Answer
We know that,
y-coordinate of any point on x-axis = 0.
By distance formula,
d =
Let point on x-axis which is equidistant from the points (2, -5) and (-2, 9) be P(x, 0).
∴ Distance between (2, -5) and (x, 0) = Distance between (-2, 9) and (x, 0).
On squaring both sides,
P = (x, 0) = (-7, 0).
Hence, required point is (-7, 0).
Find the value of x such that PQ = QR where the coordinates of P, Q and R are (6, -1), (1, 3) and (x, 8) respectively.
Answer
By distance formula,
d =
Given, PQ = QR.
∴ Distance between (6, -1) and (1, 3) = Distance between (1, 3) and (x, 8).
On squaring both sides,
Hence, x = -3 or 5.
If Q(0, 1) is equidistant from P(5, -3) and R(x, 6), find the values of x.
Answer
By distance formula,
d =
Given,
∴ Distance between Q(0, 1) and P(5, -3) = Distance between Q(0, 1) and R(x, 6).
On squaring both sides,
Hence, x = ±4.
Find a relation between x and y such that point (x, y) is equidistant from the points (7, 1) and (3, 5).
Answer
By distance formula,
d =
Given,
∴ Distance between (x, y) and (7, 1) = Distance between (x, y) and (3, 5).
On squaring both sides,
Hence, relation between x and y is x - y = 2.
The x-coordinate of a point P is twice its y-coordinate. If P is equidistant from the points Q(2, -5) and R(-3, 6), then find the coordinates of P.
Answer
Let y-coordinate of point P be k.
∴ x-coordinate = 2k.
P = (2k, k)
By distance formula,
d =
Given,
P is equidistant from the points Q(2, -5) and R(-3, 6).
On squaring both sides,
P = (2k, k) = (16, 8).
Hence, coordinates of P = (16, 8).
If the points A(4, 3) and B(x, 5) are on a circle with center C(2, 3), find the values of x.
Answer
Given,
A(4, 3) and B(x, 5) are on a circle with center C(2, 3).

∴ AC = BC [Radius of same circle]
By distance formula,
d =
Substituting values in above equation, we get :
On squaring both sides,
Hence, value of x = 2.
If a point A(0, 2) is equidistant from the points B(3, p) and C(p, 5), then find the value of p.
Answer
By distance formula,
d =
Given,
AB = AC.
On squaring both sides,
Hence, p = 1.
Using distance formula, show that (3, 3) is the center of the circle passing through the points (6, 2), (0, 4) and (4, 6).
Answer
Given,
Center (O) = (3, 3)
Let, A = (6, 2), B = (0, 4) and C = (4, 6).
By distance formula,
Since, AO = BO = CO.
Hence, proved that (3, 3) is the center of the circle passing through the points (6, 2), (0, 4) and (4, 6).
The center of a circle is C(2α - 1, 3α + 1) and it passes through the point A(-3, -1). If a diameter of the circle is of length 20 units, find the value(s) of α.
Answer
Given,
Diameter = 20 units
Radius = = 10 units.
∴ AC = 10 units
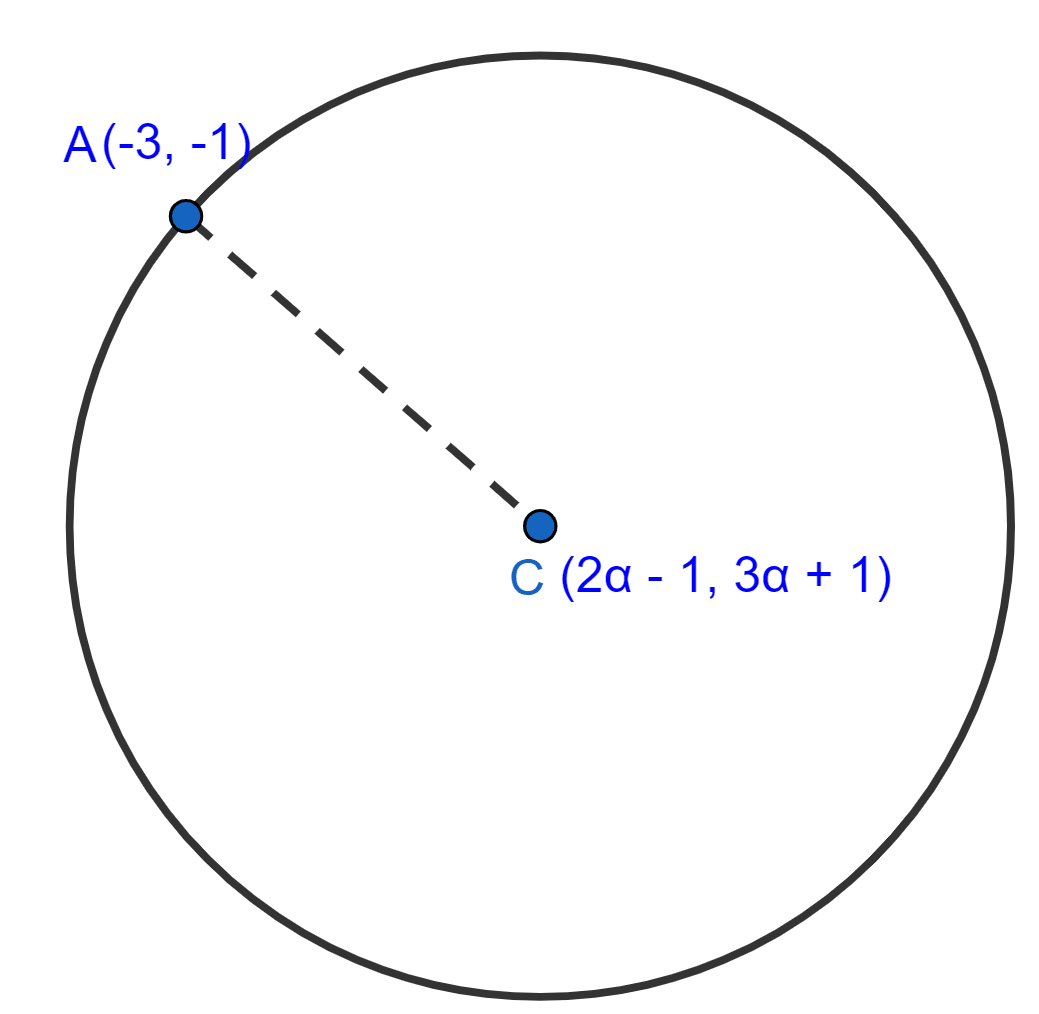
On squaring both sides,
Hence, α = or α = 2.
Using distance formula, show that the points A(3, 1), B(6, 4) and C(8, 6) are collinear.
Answer
By distance formula,
d =
Thus, AC = AB + BC.
Hence, proved that A, B and C are collinear.
Check whether the points (5, -2), (6, 4) and (7, -2) are the vertices of an isosceles triangle.
Answer
Let points be A(5, -2), B(6, 4) and C(7, -2).

By distance formula,
d =
Since, AB = BC.
Hence, proved that (5, -2), (6, 4) and (7, -2) are the vertices of an isosceles triangle.
Name the type of triangle formed by the points A(-5, 6), B(-4, -2) and C(7, 5).
Answer
By distance formula,

d =
Since, AB ≠ BC ≠ AC.
Hence, ABC is a scalene triangle.
Show that the points A(1, 1), B(-1, -1) and C(-) form an equilateral triangle.
Answer
By distance formula,

d =
Since, AB = BC = AC.
Hence, ABC is an equilateral triangle.
Show that the points (7, 10), (-2, 5) and (3, -4) are the vertices of an isosceles right triangle.
Answer
Let points be A(7, 10), B(-2, 5) and C(3, -4).

By distance formula,
d =
⇒ AB2 + BC2 =
= 106 + 106
= 212
= AC2.
Since, AB = BC and AB2 + BC2 = AC2.
∴ ABC is an isosceles right angle triangle, right angled at B.
Hence, proved that (7, 10), (-2, 5) and (3, -4) are the vertices of an isosceles triangle.
The points A(0, 3), B(-2, a) and C(-1, 4) are the vertices of a right angled triangle at A, find the value of a.
Answer
By distance formula,

d =
By pythagoras theorem,
AB2 + AC2 = BC2
Hence, value of a = 1.
Show that the points (0, -1), (-2, 3), (6, 7) and (8, 3), taken in order, are the vertices of a rectangle. Also find its area.
Answer
Let A(0, -1), B(-2, 3), C(6, 7) and D(8, 3).

By distance formula,
d =
Since, AB = CD and BC = AD.
∴ ABCD is a rectangle.
Area of rectangle ABCD = AB × BC
Hence, area of rectangle = 40 sq. units.
If P(2, -1), Q(3, 4), R(-2, 3) and S(-3, -2) be four points in a plane, show that PQRS is a rhombus but not a square. Find the area of the rhombus.
Answer
By distance formula,
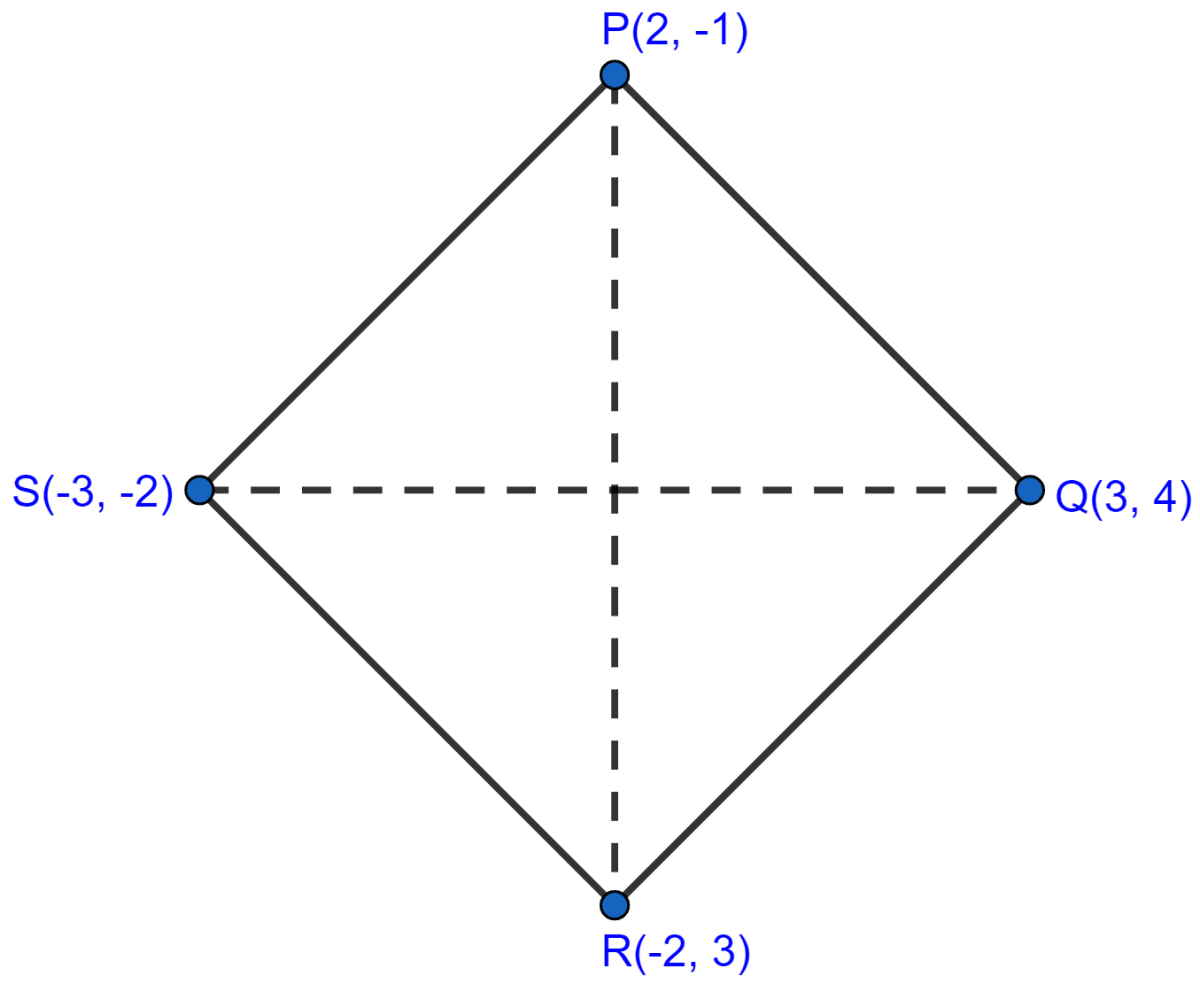
d =
Here, PQ = QR = RS = PS.
So, PQRS can be a square or rhombus.
Calculating diagonal,
PR ≠ QS.
Since, diagonal of rhombus are not equal,
∴ PQRS is a rhombus
Area of rhombus =
=
= = 24 sq. units.
Hence, PQRS is a rhombus and area = 24 sq. units.
Prove that the points A(2, 3), B(-2, 2), C(-1, -2) and D(3, -1) are the vertices of a square ABCD.
Answer
By distance formula,

d =
Calculating diagonals,
Since, AB = BC =CD = AD and AC = BD.
Hence, proved that A, B, C and D are the vertices of a square.
Name the type of quadrilateral formed by the following points and give reasons for your answer :
(-1, -2), (1, 0), (-1, 2), (-3, 0).
Answer
Let coordinates be A(-1, -2), B(1, 0), C(-1, 2) and D(-3, 0).
Since, AB = BC = CD = AD.
So, ABCD can be square or rhombus.
Calculating diagonal,
Since, diagonals are also equal.
Hence, (-1, -2), (1, 0), (-1, 2), (-3, 0) are the vertices of a square.
Name the type of quadrilateral formed by the following points and give reasons for your answer :
(4, 5), (7, 6), (4, 3), (1, 2)
Answer
Let A(4, 5), B(7, 6), C(4, 3), D(1, 2) are the given points.
By distance formula,
Calculating diagonals :
Since, opposite sides are equal and diagonals are not equal.
Hence, (4, 5), (7, 6), (4, 3), (1, 2) are the vertices of a parallelogram.
Find the coordinates of the circumcentre of the triangle whose vertices are (8, 6), (8, -2) and (2, -2). Also, find its circumradius.
Answer
Let O(x, y) be the circumcentre of the circle.
Let A(8, 6), B(8, -2) and C(2, -2) be the vertices of the triangle.
OB = OC [Radii of same circle]

By distance formula,
Squaring both sides we get,
Also,
OA = OB [Radii of same circle]
By distance formula,
On squaring both sides,
O = (x, y) = (5, 2).
Radius = OA.
Hence, circumcenter = (5, 2) and circumradius = 5 units.
Point (-3, 5) lies in the
first quadrant
second quadrant
third quadrant
fourth quadrant
Answer
In second quadrant,
x-coordinate is negative and y-coordinate is positive.
∴ P(-3, 5) lies in second quadrant.
Hence, Option 2 is the correct option.
Point (0, -7) lies
on the x-axis
in the second quadrant
on the y-axis
in the fourth quadrant
Answer
x-coordinate of any point on y-axis = 0.
∴ P(0, -7) lies on y-axis.
Hence, Option 3 is the correct option.
Abscissa of a point is positive in
I and II quadrants
I and IV quadrants
I quadrant only
II quadrants only
Answer
Abscissa (or x-coordinate) is positive in I and IV quadrants.
Hence, Option 2 is the correct option.
The point which lies on y-axis at a distance of 5 units in the negative direction of y-axis is
(0, 5)
(5, 0)
(0, -5)
(-5, 0)
Answer
Let point be P(x, y).
Since,
Point lies on y-axis.
∴ x = 0.
Also, point is at a distance of 5 units in the negative direction of y-axis.
∴ y = -5.
P = (x, y) = (0, -5).
Hence, Option 3 is the correct option.
If the perpendicular distance of a point P from the x-axis is 5 units and the foot of perpendicular lies on the negative direction of x-axis, then the point P has
x-coordinate = -5
y-coordinate = 5 only
y-coordinate = -5 only
y-coordinate = 5 or -5
Answer
In graph, let 1 block = 1 unit.

Since,
Perpendicular distance of a point P from the x-axis is 5 units and the foot of perpendicular lies on the negative direction of x-axis.
Let foot of perpendicular be B.
So, position of point P can be A or C.
From graph,
The y-coordinate of A and C = 5 and -5.
Hence, Option 4 is the correct option.
The points whose abscissa and ordinate have different signs will lie in
I and II quadrants
II and III quadrants
I and III quadrants
II and IV quadrants
Answer
In second quadrant,
x-coordinate is negative and y-coordinate is positive.
In fourth quadrant,
x-coordinate is positive and y-coordinate is negative.
Hence, points having opposite signs lie in II and IV quadrants.
Hence, Option 4 is the correct option.
The points (-5, 2) and (2, -5) lie in
same quadrant
II and III quadrants respectively
II and IV quadrants respectively
IV and II quadrants respectively
Answer
In second quadrant,
x-coordinate is negative and y-coordinate is positive.
∴ (-5, 2) lies in II quadrant.
In fourth quadrant,
x-coordinate is positive and y-coordinate is negative.
∴ (2, -5) lies in IV quadrant.
Hence, Option 3 is the correct option.
If P(-1, 1), Q(3, -4), R(1, -1), S(-2, -3) and T(-4, 4) are plotted on the graph paper, then point(s) in the fourth quadrant are
P and T
Q and R
S only
P and R
Answer
From graph,

Q and R lies in fourth quadrant.
Hence, Option 2 is the correct option.
On plotting the points O(0, 0), A(3, 0), B(3, 4), C(0, 4) and joining OA, AB, BC, and CO which of the following figure is obtained?
Square
Rectangle
Trapezium
Rhombus
Answer
From graph,

OA = BC = 3 units
OC = AB = 4 units
∴ Figure obtained is a rectangle.
Hence, Option 2 is the correct option.
Which of the following points lie on the graph of the equation :
3x - 5y + 7 = 0?
(1, -2)
(2, 1)
(-1, 2)
(1, 2)
Answer
Substituting (1, -2) in L.H.S. of the equation 3x - 5y + 7 = 0, we get :
⇒ 3x - 5y + 7
⇒ 3(1) - 5(-2) + 7
⇒ 3 + 10 + 7
⇒ 20
Since, L.H.S. ≠ R.H.S., (1, -2) does not satisfy the equation.
Substituting (2, 1) in L.H.S. of the equation 3x - 5y + 7 = 0, we get :
⇒ 3x - 5y + 7
⇒ 3(2) - 5(1) + 7
⇒ 6 - 5 + 7
⇒ 8
Since, L.H.S. ≠ R.H.S., (2, 1) does not satisfy the equation.
Substituting (-1, 2) in L.H.S. of the equation 3x - 5y + 7 = 0, we get :
⇒ 3x - 5y + 7
⇒ 3(-1) - 5(2) + 7
⇒ -3 - 10 + 7
⇒ -6
Since, L.H.S. ≠ R.H.S., (-1, 2) does not satisfy the equation.
Substituting (1, 2) in L.H.S. of the equation 3x - 5y + 7 = 0, we get :
⇒ 3x - 5y + 7
⇒ 3(1) - 5(2) + 7
⇒ 3 - 10 + 7
⇒ 0
Since, L.H.S. = R.H.S., (1, 2) satisfies the equation.
Hence, Option 4 is the correct option.
The pair of equation x = a and y = b graphically represents lines which are
parallel
intersecting at (b, a)
coincident
intersecting at (a, b)
Answer
From graph,

x = a and y = b intersects at (a, b).
Hence, Option 4 is the correct option.
The distance of the point P(2, 3) from the x-axis is
2 units
3 units
1 unit
5 units
Answer
The distance between the point P(2, 3) and x-axis can be determined by assuming a point A(2, 0) on x-axis.
By distance formula,
Hence, Option 2 is the correct option.
The distance of the point P(-4, 3) from the y-axis is
5 units
-4 units
4 units
3 units
Answer
The distance between the point P(-4, 3) and y-axis can be determined by assuming a point A(0, 3) on y-axis.
By distance formula,
Hence, Option 3 is the correct option.
The distance of the point P(-6, 8) from the origin is
8 units
units
10 units
6 units
Answer
Origin (O) = (0, 0) and P = (-6, 8).
By distance formula,
Hence, Option 3 is the correct option.
The distance between the points A(0, 6) and B(0, -2) is
6 units
8 units
4 units
2 units
Answer
By distance formula,
Hence, Option 2 is the correct option.
The distance between the points (0, 5) and (-5, 0) is
5 units
units
units
10 units
Answer
Let, A = (0, 5) and B = (-5, 0).
By distance formula,
Hence, Option 2 is the correct option.
AOBC is a rectangle whose three vertices are A(0, 3), O(0, 0) and B(5, 0). The length of its diagonal is
5 units
3 units
units
4 units
Answer
Since, AOBC is the rectangle.
So, AB will be the diagonal.

By distance formula,
Hence, Option 3 is the correct option.
If the distance between the points (2, -2) and (-1, x) is 5 units, then one of the value of x is
-2
2
-1
1
Answer
By distance formula,
d =
Given,
Distance between (2, -2) and (-1, x) is 5 units.
As distance cannot be negative,
∴ x = 2
Hence, Option 2 is the correct option.
The distance between the points (4, p) and (1, 0) is 5 units, then the value of p is
4 only
-4 only
±4
0
Answer
By distance formula,
d =
Given,
Distance between (4, p) and (1, 0) is 5 units.
Hence, Option 3 is the correct option.
The points (-4, 0), (4, 0) and (0, 3) are the vertices of a
right triangle
isosceles triangle
equilateral triangle
scalene triangle
Answer
Let A = (-4, 0), B = (4, 0) and C = (0, 3).

By distance formula,
Since, AC = BC.
∴ ABC is an isosceles triangle.
Hence, Option 2 is the correct option.
The area of a square whose vertices are A(0, -2), B(3, 1), C(0, 4) and D(-3, 1) is
18 sq. units
15 sq. units
units
units
Answer
By distance formula,

Area of square = (side)2 = AB2
= = 18 sq. units.
Hence, Option 1 is the correct option.
In the adjoining figure, the area of triangle ABC is
15 sq. units
10 sq. units
7.5 sq. units
2.5 sq. units

Answer
Draw a perpendicular AD from A on x-axis.

From graph,
D = (1, 0).
By distance formula,
Area of triangle = base × height
=
= = 7.5 sq. units
Hence, Option 3 is the correct option.
The perimeter of a triangle with vertices (0, 4), (0, 0) and (3, 0) is
5 units
12 units
11 units
7 + units
Answer
Let A(0, 4), B(0, 0) and C(3, 0) be the vertices of the triangle.

By distance formula,
Perimeter = AB + BC + AC = 4 + 3 + 5 = 12 units.
Hence, Option 2 is the correct option.
If A is a point on the y-axis whose ordinate is 5 and B is the point (-3, 1), then the length of AB is
8 units
5 units
3 units
25 units
Answer
Since, A is a point on y-axis, so x-coordinate = 0.
A = (0, 5).
B = (-3, 1).
By distance formula,
Hence, Option 2 is the correct option.
The points A(9, 0), B(9, 6), C(-9, 6) and D(-9, 0) are the vertices of a
rectangle
square
rhombus
trapezium
Answer
By distance formula,

Since, AB = CD and BC = AD.
∴ ABCD is a rectangle.
Hence, Option 1 is the correct option.
Consider the following two statements:
Statement 1: The point (x2, y) lies on the y - axis. Then the value of x is zero.
Statement 2: The abscissa of every point on y-axis is zero.
Which of the following is valid?
Both the statements are true.
Both the statements are false.
Statement 1 is true, and Statement 2 is false.
Statement 1 is false, and Statement 2 is true.
Answer
Any point that lies on the y-axis has its x-coordinate equal to zero.
The given point is (x2, y).
For this point to lie on the y-axis, its x-coordinate, which is x2, must be equal to zero.
So, x2 = 0.
If x2 = 0, then x must be 0.
∴ Statement 1 is true.
The abscissa is the x-coordinate of a point in a Cartesian coordinate system.
All points on the y-axis are of the form (0, y), where y can be any real number.
For any point on the y-axis, its x-coordinate (abscissa) is 0.
∴ Statement 2 is true.
∴ Both the statements are true.
Hence, option 1 is correct option.
Assertion (A): Two ordered pairs (a, b) and (c, d) are equal if a = c and b = d.
Reason (R): If a ≠ b, then (a, b) ≠ (b, a).
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Answer
Two ordered pairs (a, b) and (c, d) are equal if a = c and b = d.
This statement is the definition of equality for ordered pairs. For two ordered pairs to be considered equal, their corresponding elements must be equal.
So, (a, b) = (c, d) if and only if a = c and b = d.
∴ Assertion (A) is true.
If a ≠ b, then (a, b) ≠ (b, a).
For example, the ordered pair (2, 3) is not the same as (3,2). They represent different points in a coordinate plane.
∴ Reason (R) is true.
∴ Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Hence, option 4 is the correct option.
Assertion (A): The point P(3, -5) lies in quadrant II and the point Q(-2, -1) lies in quadrant III.
Reason (R): The signs of a point in I, II, III and IV quadrants are respectively (+, +), (-, +), (-, -) and (+, -).
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Answer
Point P(3, -5):
The x-coordinate is positive, and the y-coordinate is negative.
A point with a positive x-coordinate and a negative y-coordinate lies in quadrant IV.
Point Q(-2, -1):
The x-coordinate is negative, and the y-coordinate is negative.
A point with a negative x-coordinate and a negative y-coordinate lies in quadrant III.
∴ Assertion (A) is false.
Quadrant I: x-coordinate is positive, y-coordinate is positive (+, +).
Quadrant II: x-coordinate is negative, y-coordinate is positive (-, +).
Quadrant III: x-coordinate is negative, y-coordinate is negative (-, -).
Quadrant IV: x-coordinate is positive, y-coordinate is negative (+, -).
∴ Reason (R) is true.
∴ Assertion (A) is false, Reason (R) is true.
Hence, option 2 is the correct option.
Assertion (A): Two points A and B having coordinates (3, 3) and (-3, -3) respectively are joined. The line segment AB passes through the origin.
Reason (R): Origin is the point of intersection of the coordinate axes.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Answer
When a point (x,y) is reflected across the origin (0, 0), its new coordinates become (−x, −y). This transformation is also known as point symmetry with respect to the origin.
Point A has coordinates (3, 3).
If we reflect point A(3, 3) across the origin (0, 0), the coordinates of its reflected image would be (−3, −3).
The coordinates of the given point B are exactly (−3, −3).
Since point B is the exact reflection of point A across the origin, it means that the origin (0, 0) lies precisely on the straight line segment connecting point A and point B.
Therefore, the line segment AB passes through the origin.
∴ Assertion (A) is true.
Origin is the point of intersection of the coordinate axes.
This is the definition of the origin in a Cartesian coordinate system. It's the point where the x-axis and y-axis intersect, and its coordinates are (0, 0).
∴ Reason (R) is true.
∴ Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Hence, option 4 is the correct option.
Assertion (A): If the points A(2, 9), B(2, 5) and C(5, 5) are joined, then ΔABC is right angled.
Reason (R): If AC2 = AB2 + BC2, then ∠B = 90°.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Answer
Given, the points A(2, 9), B(2, 5) and C(5, 5).
By distance formula,
Distance between two points =
Given, points A(2, 9), B(2, 5) and C(5, 5).
AC2 = 52 = 25 units
AB2 = 42 = 16 units
BC2 = 32 = 9 units
Since, AC2 = AB2 + BC2, thus it satisfies pythagoras theorem.
Thus, ABC is a right angled triangle at B.
Thus, Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Hence, option 3 is the correct option.
Assertion (A): Point (0, 9) is a point on y-axis which is equidistant from points (6, 5) and (-4, 3).
Reason (R): Abscissa of a point on y-axis is 0.
Assertion (A) is true, Reason (R) is false.
Assertion (A) is false, Reason (R) is true.
Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).
Answer
A point lies on the y-axis if and only if its x-coordinate (abscissa) is 0.
∴ Reason (R) is true.
Let P = (0, 9), A = (6, 5), and B = (-4, 3).
By formula,
Distance between two points =
Since PA = PB = .
Therefore, the point (0, 9) is a point on y-axis which is equidistant from (6, 5) and (-4, 3).
∴ Assertion (A) is true.
∴ Both Assertion (A) and Reason (R) are true, and Reason (R) is not the correct reason (or explanation) for Assertion (A).
Hence, option 4 is the correct option.
Three vertices of a rectangle are A(2, -1), B(2, 7) and C(4, 7). Plot these points on a graph and hence use it to find the co-ordinates of the fourth vertex D. Also find the co-ordinates of
(i) the mid-point of BC
(ii) the mid-point of CD
(iii) the point of intersection of the diagonals.
What is the area of the rectangle ?
Answer
In graph,
1 block = 1 unit.
Steps of construction :
Plot the points A(2, -1), B(2, 7) and C(4, 7) on graph.
Join AB and BC.
Measure AB. Draw a line segment CD, from point C parallel to y-axis.
Measure BC. Draw a line segment AD, from point A parallel to x-axis.
Mark F and G mid-point of BC and CD respectively.
Join AC and BD diagonals of rectangle.
Mark E as the point of intersection of diagonals.
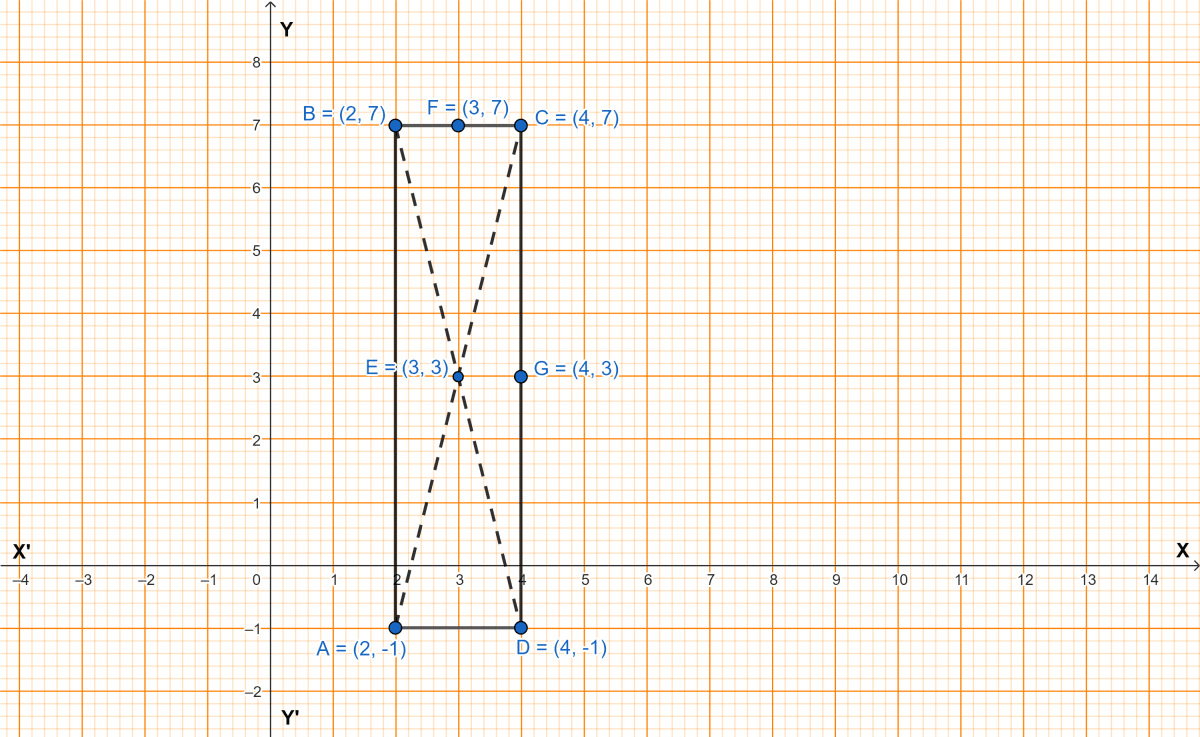
From graph,
Coordinates of D = (4, -1).
(i) From graph,
F is the mid-point of BC and F = (3, 7).
Hence, coordinates of mid-point of BC = (3, 7).
(ii) From graph,
G is the mid-point of CD and G = (4, 3).
Hence, coordinates of mid-point of CD = (4, 3).
(iii) From graph,
E is the point of intersection of diagonals.
Hence, point of intersection of the diagonals = (3, 3).
From graph,
AB = 8 units and BC = 2 units.
Area of the rectangle ABCD = length × breadth
= AB × BC
= 8 × 2
= 16 sq. units.
Hence, the area of the rectangle = 16 sq. units.
Three vertices of a parallelogram are A(3, 5), B(3, -1) and C(-1, -3). Plot these points on a graph paper and hence use it to find the coordinates of the fourth vertex D. Also find the coordinates of the mid-point of the side CD. What is the area of the parallelogram?
Answer
Steps of construction :
Plot the points A(3, 5), B(3, -1) and C(-1, -3) on graph paper.
Join AB and BC.
From C draw a line CD parallel to AB, such that CD = AB.
From A draw a line AD parallel to BC, such that AD = BC.
Mark E, the mid-point of CD.
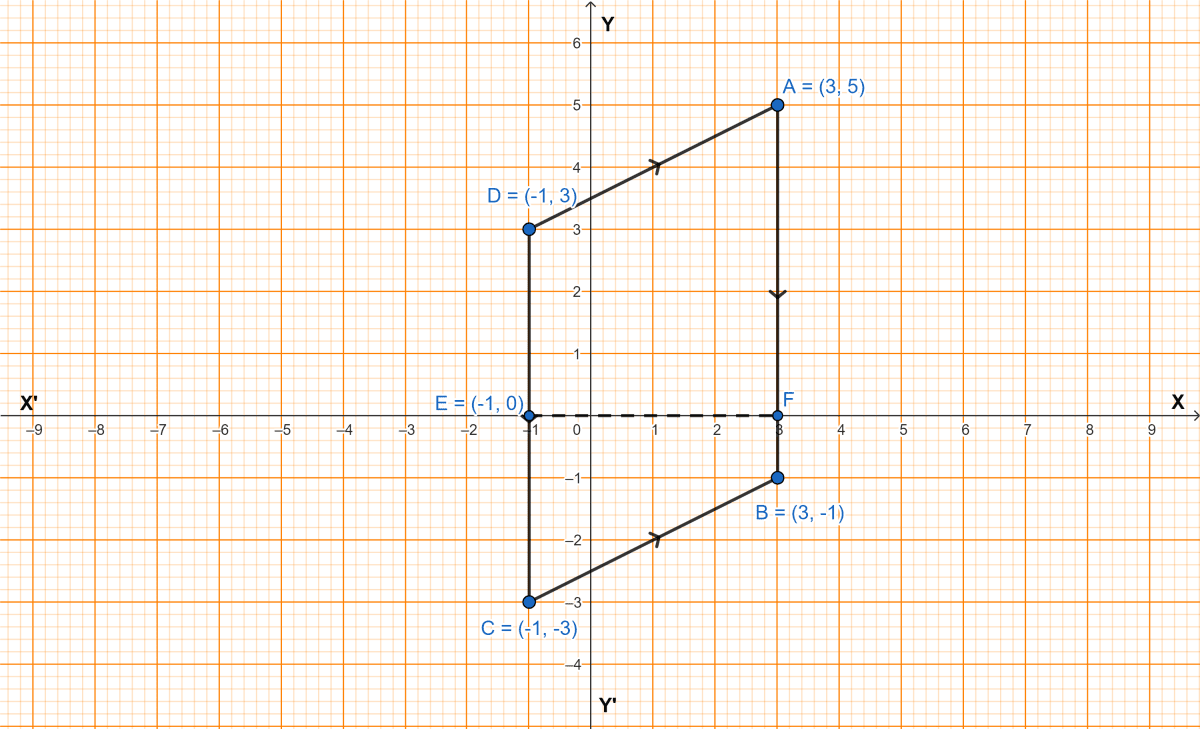
From graph,
The coordinates of fourth vertex D are (-1, 3).
The coordinates of the midpoint of CD i.e. E are (-1, 0).
As, 1 block = 1 unit
EF = 4 units
CD = 6 units
Area of parallelogram ABCD = Base × height
= CD × EF
= 6 × 4
= 24 sq. units.
Hence, D = (-1, 3), coordinates of mid-point of CD = (-1, 0) and the area of the parallelogram is 24 sq. units.
Draw the graphs of the following linear equation.
y = 2x - 1
Also find slope and y-intercept of this line.
Answer
Given,
y = 2x - 1 ..........(1)
When x = 1, y = 2 × 1 - 1 = 2 - 1 = 1
x = 2, y = 2 × 2 - 1 = 4 - 1 = 3
x = 3, y = 2 × 3 - 1 = 6 - 1 = 5.
| x | 1 | 2 | 3 |
|---|---|---|---|
| y | 1 | 3 | 5 |
Steps of construction :
Plot the points (1, 1), (2, 3) and (3, 5) on graph.
Join the points.

Comparing equation (1) with y = mx + c, we get :
m = 2 and c = -1.
Hence, slope of the line = 2 and y-intercept = -1.
Draw the graphs of the following linear equation.
2x + 3y = 6
Also find slope and y-intercept of this line.
Answer
Given,
⇒ 2x + 3y = 6
⇒ 3y = 6 - 2x
⇒ y =
⇒ y = ...........(1)
When x = 0, = 2 - 0 = 2,
x = 3, y = = 2 - 2 = 0,
x = 6, y = = 2 - 4 = -2.
| x | 0 | 3 | 6 |
|---|---|---|---|
| y | 2 | 0 | -2 |
Steps of construction :
Plot the points (0, 2), (3, 0) and (6, -2) on graph.
Join the points.

Comparing equation (1) with y = mx + c, we get :
m = and c = 2.
Hence the slope of the line = and y intercept = 2.
Draw the graphs of the following linear equation.
2x - 3y = 4
Also find slope and y-intercept of this line.
Answer
Given,
⇒ 2x - 3y = 4
⇒ 3y = 2x - 4
⇒ y =
⇒ y = ........(1)
When x = -1, y = = -2,
x = 2, y = = 0,
x = 5, y = = 2.
| x | -1 | 2 | 5 |
|---|---|---|---|
| y | -2 | 0 | 2 |
Steps of construction :
Plot the points (-1, -2), (2, 0) and (5, 2) on graph.
Join the points.

Comparing equation (1) with y = mx + c.
m = and c = .
Hence, the slope of line = and y intercept = .
Draw the graph of the equation 3x - 4y = 12. From the graph, find :
(i) the value of y when x = -4
(ii) the value of x when y = 3.
Answer
Given,
⇒ 3x - 4y = 12
⇒ 4y = 3x - 12
⇒ y =
⇒ y = .
When x = 0, y = = 0 - 3 = -3,
x = 4, y = = 3 - 3 = 0,
x = 8, y = = 6 - 3 = 3.
| x | 0 | 4 | 8 |
|---|---|---|---|
| y | -3 | 0 | 3 |
Steps of construction :
Plot the points (0, -3), (4, 0) and (8, 3) on graph.
Join the points.

(i) Steps of construction :
Take a point N (x = -4) and draw a line parallel to y-axis, touching the graph at point M.
From M draw a line parallel to x-axis touching y-axis at point O (y = -6).
Hence, when x = -4, the value of y is -6.
(ii) Steps of construction :
Take a point P (y = 3) and draw a line parallel to x-axis, touching the graph at point R.
From R draw a line parallel to y-axis touching x-axis at point Q (x = 8).
Hence, when y = 3, the value of x is 8.
Solve graphically, the simultaneous equations : 2x - 3y = 7; x + 6y = 11.
Answer
Given,
⇒ 2x - 3y = 7
⇒ 3y = 2x - 7
⇒ y = .........(1)
When, x = -1, y = = -3,
x = 2, y = = -1,
x = 5, y = = 1.
Table of values of equation (1) :
| x | -1 | 2 | 5 |
|---|---|---|---|
| y | -3 | -1 | 1 |
Steps of construction :
Plot the points (-1, -3), (2, -1) and (5, 1) on graph.
Join the points.
Given,
⇒ x + 6y = 11
⇒ 6y = 11 - x
⇒ y = ..........(2)
When x = -7, y = = 3,
x = -1, y = = 2,
x = 5, y = = 1.
Table of values of equation (2) :
| x | -7 | -1 | 5 |
|---|---|---|---|
| y | 3 | 2 | 1 |
Steps of construction :
Plot the points (-7, 3), (-1, 2) and (5, 1) on graph.
Join the points.

From graph,
The two lines intersect at P(5, 1).
Hence x = 5, y = 1.
Solve the following system of equations graphically :
x - 2y - 4 = 0, 2x + y - 3 = 0.
Answer
Given,
⇒ x - 2y - 4 = 0
⇒ 2y = x - 4
⇒ y = .........(1)
When x = -2, y = = -3,
x = 0, y = ,
x = 2, y = = -1.
Table of values of equation (1) :
| x | -2 | 0 | 2 |
|---|---|---|---|
| y | -3 | -2 | -1 |
Steps of construction :
Plot the points (-2, -3), (0, -2) and (2, -1) on graph.
Join the points.
Given,
⇒ 2x + y - 3 = 0
⇒ y = 3 - 2x .........(2)
When x = 0, y = 3 - 2(0) = 3 - 0 = 3,
x = 1, y = 3 - 2(1) = 3 - 2 = 1,
x = 2, y = 3 - 2(2) = 3 - 4 = -1.
Table of values of equation (2) :
| x | 0 | 1 | 2 |
|---|---|---|---|
| y | 3 | 1 | -1 |
Steps of construction :
Plot the points (0, 3), (1, 1) and (2, -1) on graph.
Join the points.
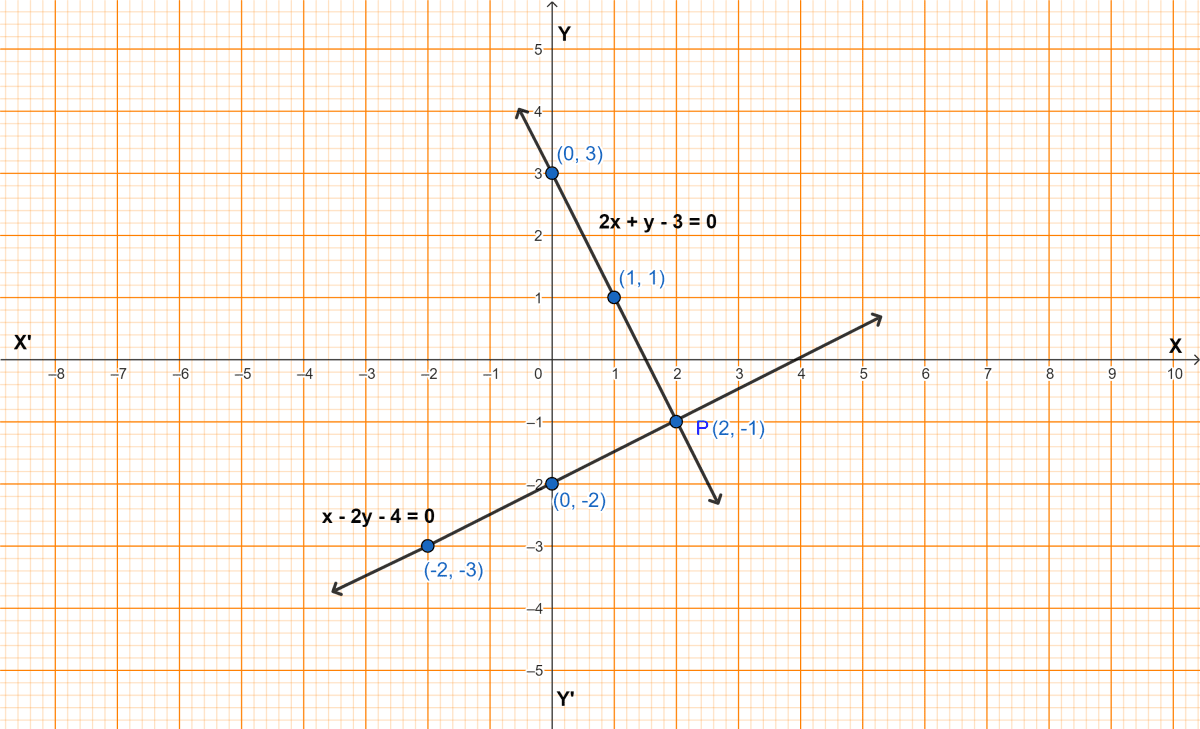
From graph,
The lines intersect each other at P(2, -1).
Hence, x = 2, y = -1.
Using a scale of 1 cm to 1 unit for both the axes, draw the graphs of the following equations: 6y = 5x + 10, y = 5x - 15. From the graph, find
(i) the coordinates of the point where the two lines intersect.
(ii) the area of the triangle between the lines and the x-axis.
Answer
(i) Given,
⇒ 6y = 5x + 10
⇒ y = .........(1)
When x = 1, y = = 2.5
x = -2, y = = 0,
x = 4, y = = 5.
Table of values of equation (1) :
| x | 1 | -2 | 4 |
|---|---|---|---|
| y | 2.5 | 0 | 5 |
Steps of construction :
Plot the points (1, 2.5), (-2, 0) and (4, 5) on graph.
Join the points.

Given,
y = 5x - 15
When x = 2.5, y = 5 × 2.5 - 15 = 12.5 - 15 = -2.5,
x = 3, y = 5 × 3 - 15 = 15 - 15 = 0,
x = 4, y = 5 × 4 - 15 = 20 - 15 = 5.
Table of values of equation (2) :
| x | 2.5 | 3 | 4 |
|---|---|---|---|
| y | -2.5 | 0 | 5 |
Steps of construction :
Plot the points (2.5, -2.5), (3, 0) and (4, 5) on graph.
Join the points.
From graph,
The lines intersect at point P(4, 5).
Hence, x = 4, y = 5.
(ii) From graph,
Triangle = PQR.
Draw a line PJ, from P perpendicular to x-axis.
PJ = 5 units
QR = 5 units
Area of triangle = × base × height
= × QR × PJ
= × 5 × 5
=
= 12.5 sq. units.
Hence, area = 12.5 sq. units.
Find, graphically, the coordinates of the vertices of the triangle formed by the lines:
8y - 3x + 7 = 0, 2x - y + 4 = 0 and 5x + 4y = 29.
Answer
Given,
⇒ 8y - 3x + 7 = 0
⇒ 8y = 3x - 7
⇒ y = .........(1)
When x = -3, y = = -2,
x = 1, y = = -0.5
x = 5, y = = 1.
Table of values of equation (1) :
| x | -3 | 1 | 5 |
|---|---|---|---|
| y | -2 | -0.5 | 1 |
Steps of construction :
Plot the points (-3, -2), (1, -0.5), (5, 1) on graph.
Join the points.
Given,
⇒ 2x - y + 4 = 0
⇒ y = 2x + 4
When x = -2, y = 2(-2) + 4 = -4 + 4 = 0,
x = -1, y = 2(-1) + 4 = -2 + 4 = 2,
x = 0, y = 2(0) + 4 = 0 + 4 = 4.
Table of values of equation (2) :
| x | -2 | -1 | 0 |
|---|---|---|---|
| y | 0 | 2 | 4 |
Steps of construction :
Plot the points (-2, 0), (-1, 2), (0, 4) on graph.
Join the points.
Given,
⇒ 5x + 4y = 29
⇒ 4y = 29 - 5x
⇒ y = ..........(3)
When x = 1, y = = 6,
x = 3, y = = 3.5,
x = 5, y = = 1.
Table of values of equation (3) :
| x | 1 | 3 | 5 |
|---|---|---|---|
| y | 6 | 3.5 | 1 |
Steps of construction :
Plot the points (1, 6), (3, 3.5), (5, 1) on graph.
Join the points.
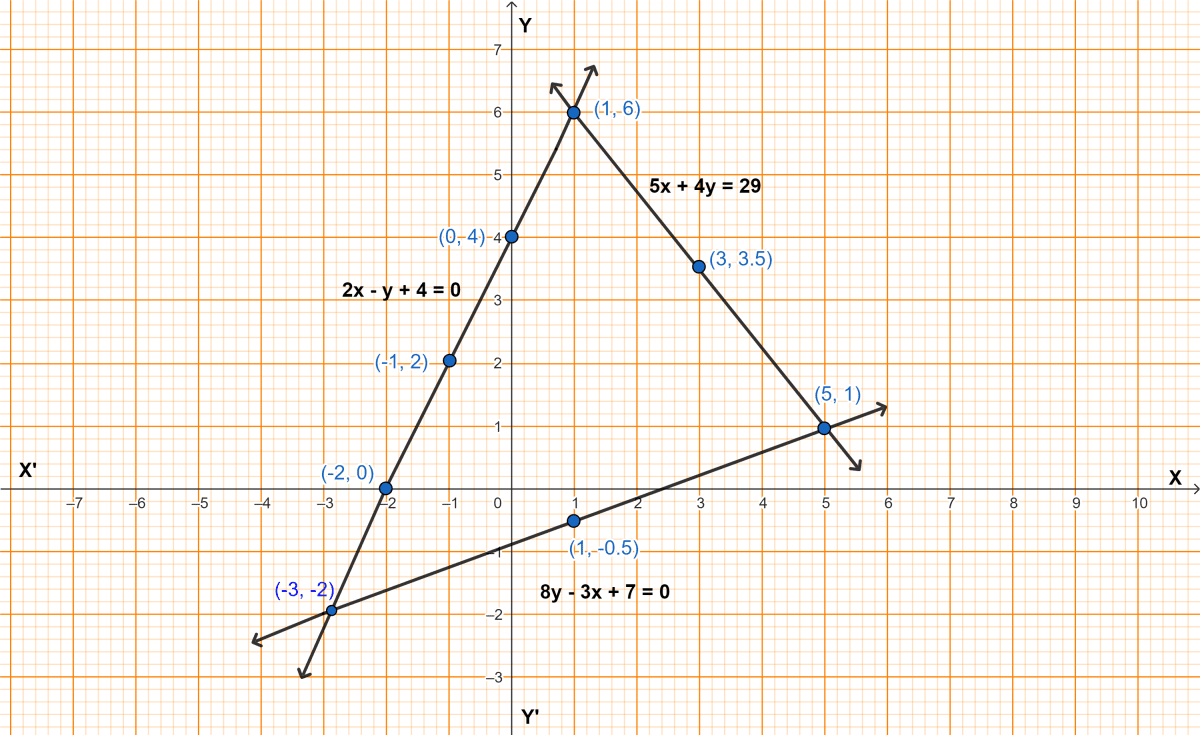
From graph,
These three lines intersect each other at (-3, -2), (5, 1) and (1, 6).
Hence, the coordinates of the vertices of the triangle formed by these lines are (-3, -2), (5, 1) and (1, 6).
Find graphically the coordinates of the vertices of the triangle formed by the lines y - 2 = 0, 2y + x = 0 and y + 1 = 3 (x - 2). Hence, find the area of the triangle formed by these lines.
Answer
Given,
⇒ y - 2 = 0
⇒ y = 2 ........(1)
Given,
⇒ 2y + x = 0
⇒ 2y = -x
⇒ y = - ............(2)
When, x = -2, y = = 1,
x = 0, y = = 0,
x = 2, y = = -1.
Table of equation (2) :
| x | -2 | 0 | 2 |
|---|---|---|---|
| y | 1 | 0 | -1 |
Steps of construction :
Plot the points (-2, 1), (0, 0), (2, -1) on graph.
Join the points.
Given,
⇒ y + 1 = 3(x - 2)
⇒ y + 1 = 3x - 6
⇒ y = 3x - 6 - 1
⇒ y = 3x - 7 ...........(3)
When x = 1, y = 3 × 1 - 7 = 3 - 7 = -4,
x = 2, y = 3 × 2 - 7 = 6 - 7 = -1,
x = 3, y = 3 × 3 - 7 = 9 - 7 = 2.
Table of equation (3) :
| x | 1 | 2 | 3 |
|---|---|---|---|
| y | -4 | -1 | 2 |
Steps of construction :
Plot the points (1, -4), (2, -1), (3, 2) on graph.
Join the points.
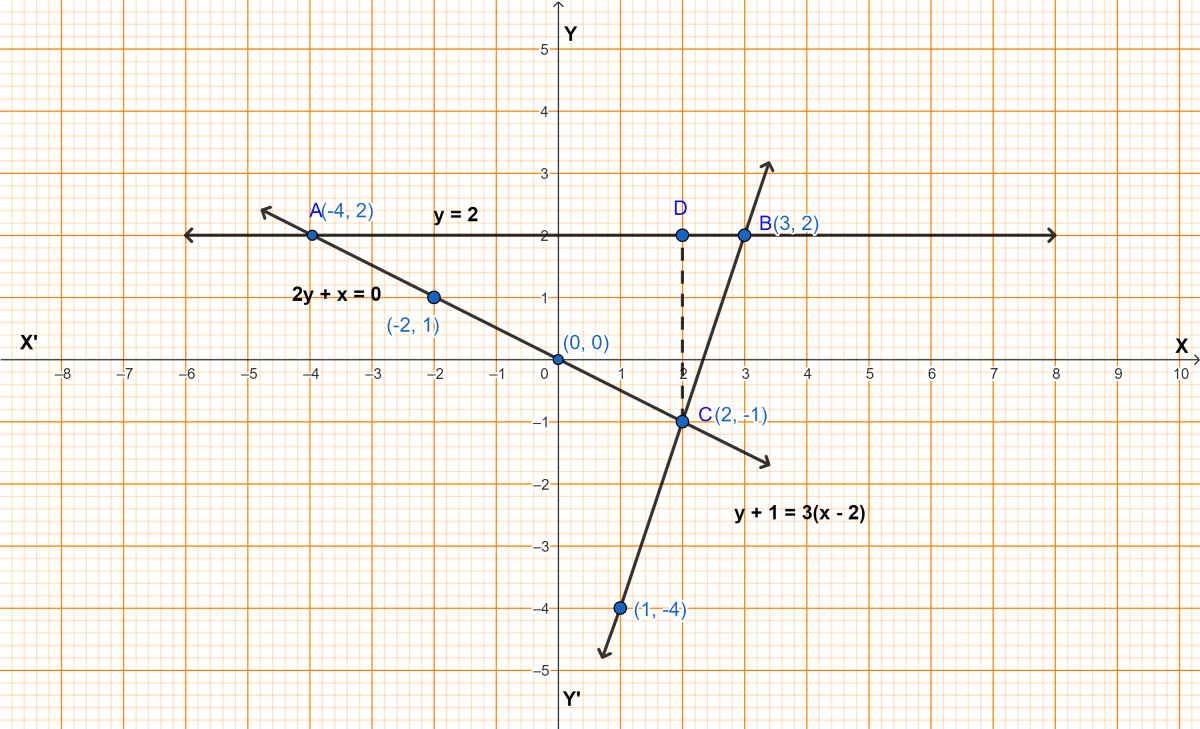
From graph,
A(-4, 2), B(3, 2), C(2, -1) are the vertices of the triangle.
From C, draw CD perpendicular to AB.
As, 1 block = 1 unit.
AB = 7 units and CD = 3 units
Area of triangle = × base × height
= × AB × CD
= × 7 × 3
= = 10.5 sq. units
Hence, coordinates of the vertices of the triangle are (-4, 2), (3, 2), (2, -1) and area = 10.5 sq. units.
A line segment is of length 10 units and one of its end is (-2, 3). If the ordinate of the other end is 9, find the abscissa of the other end.
Answer
Given,
Ordinate of the point on the other end = 9.
Let abscissa = x.
Given,
Distance between the two ends (-2, 3) and (x, 9) = 10 units.
By distance formula,
On squaring both sides,
Hence, abscissa of other end = 6 or -10.
A(-4, -1), B(-1, 2) and C(α, 5) are the vertices of an isosceles triangle. Find the value of α given that AB is the unequal side.
Answer
It is given that
A(-4, -1), B(-1, 2) and C(α, 5) are the vertices of an isosceles triangle and AB is the unequal side.
∴ AC = BC.

By distance formula,
Since, AC = BC
On squaring both sides we get,
Hence, α = -7.
If A(-3, 2), B(α, β) and C(-1, 4) are the vertices of an isosceles triangle, prove that α + β = 1, given AB = BC.
Answer
Given,
A(-3, 2), B(α, β) and C(-1, 4) are the vertices of an isosceles triangle
By distance formula,
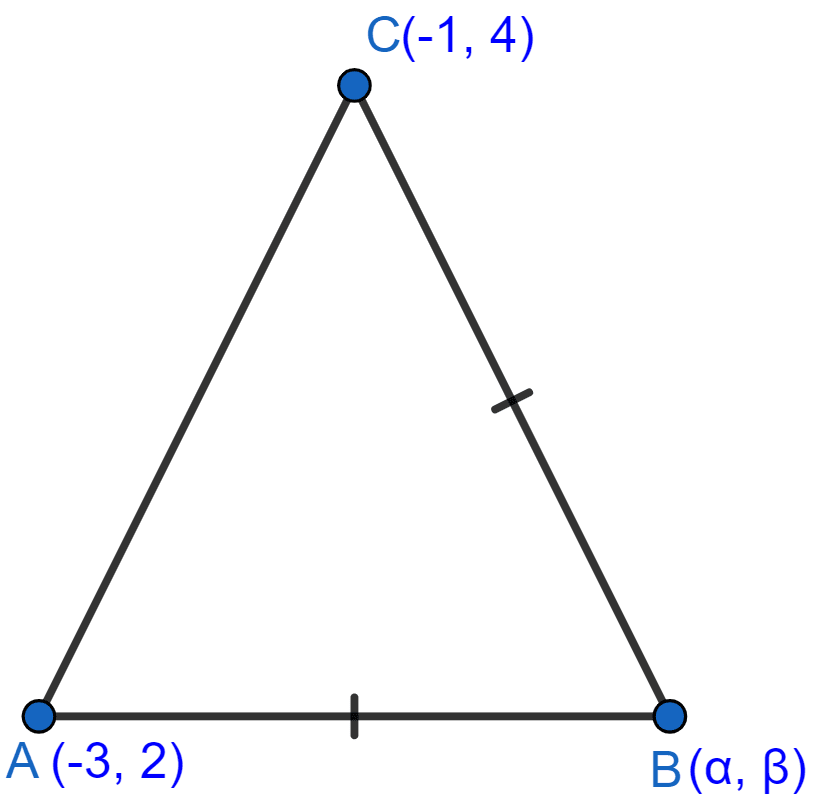
As, AB = BC
On squaring both sides,
Hence, proved that α + β = 1.
Prove that the points (3, 0), (6, 4) and (-1, 3) are the vertices of a right angled isosceles triangle.
Answer
Let the points be A(3, 0), B(6, 4) and C(-1, 3).
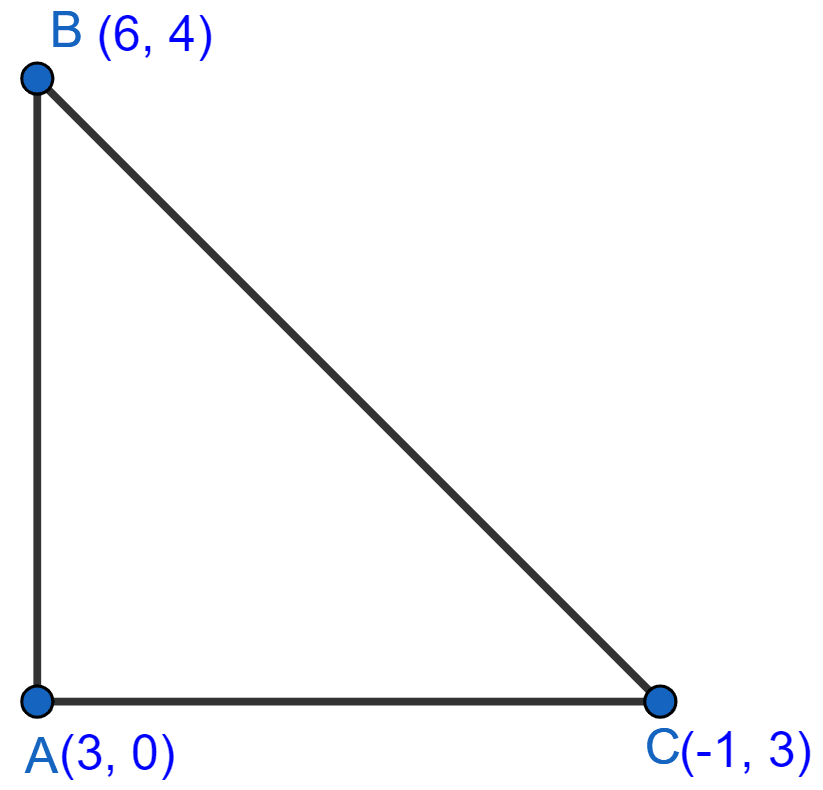
By distance formula,
∴ AB = AC = 5
∴ ΔABC is an isosceles triangle
AB2 + AC2 = 52 + 52
= 25 + 25
= 50.
BC2 = = 50.
Since, AB2 + AC2 = BC2.
Hence, proved that (3, 0), (6, 4) and (-1, 3) are the vertices of a right angled isosceles triangle.
Show that the points (2, 1), (0, 3), (-2, 1) and (0, -1), taken in order, are the vertices of a square. Also find the area of the square.
Answer
Let A(2, 1), B(0, 3), C(-2, 1) and D(0, -1) be the four points.

By distance formula,
Since, AB = BC = CD = AD i.e. all sides are equal so, ABCD can be a rhombus or a square.
Calculating diagonals,
Since, diagonals are equal.
∴ ABCD is a square.
Area of square = (side)2
= (AB)2
=
= 8 sq. units.
Hence, proved that (2, 1), (0, 3), (-2, 1) and (0, -1), taken in order, are the vertices of a square and area = 8 sq. units.
Show that the points (-3, 2), (-5, -5), (2, -3) and (4, 4), taken in order, are the vertices of rhombus. Also, find its area. Do the given points form a square?
Answer
Let A(-3, 2), B(-5, -5), C(2, -3) and D(4, 4).

By distance formula,
Calculating diagonals,
Since, all sides are equal and diagonals are not equal.
∴ ABCD is a rhombus.
Area of rhombus =
Hence, ABCD is a rhombus and area = 45 sq. units.
The ends of a diagonal of a square have co-ordinates (-2, p) and (p, 2). Find p if the area of the square is 40 sq. units.
Answer
Given,
Ends of a diagonal of a square are (-2, p) and (p, 2).
Area of square = 40 sq. units
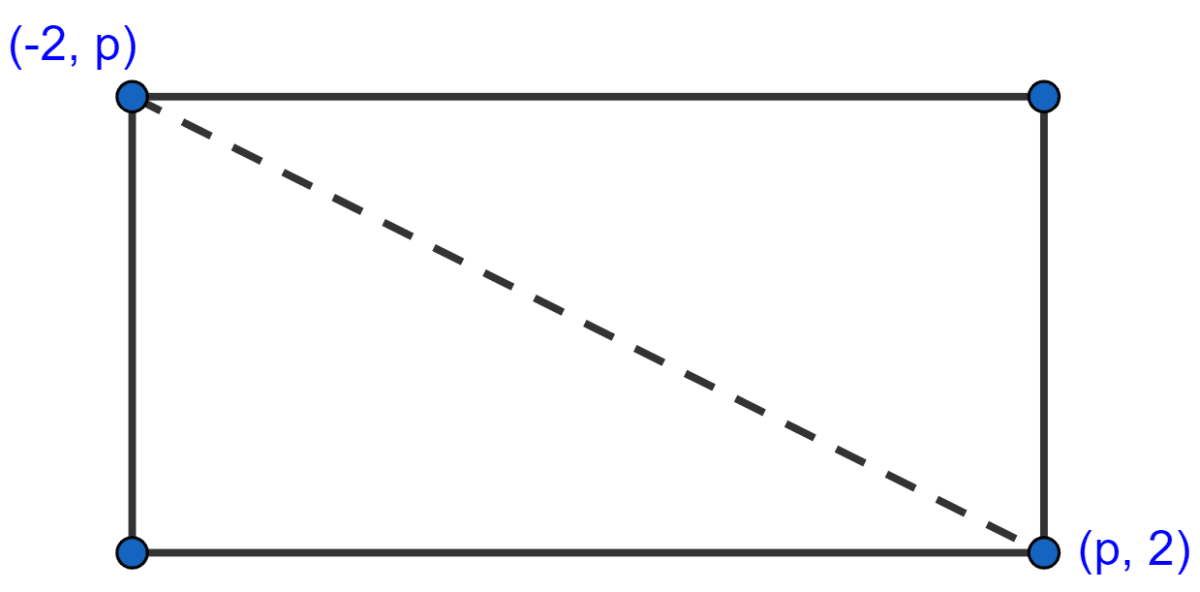
By formula,
Area of square = (side)2
∴ (side)2 = 40
⇒ side = units.
By formula,
Diagonal of a square = × side = .
By distance formula,
On squaring both sides,
Hence, p = ±6.
What type of quadrilateral do the points A(2, -2), B(7, 3), C(11, -1) and D(6, -6), taken in that order, form?
Answer
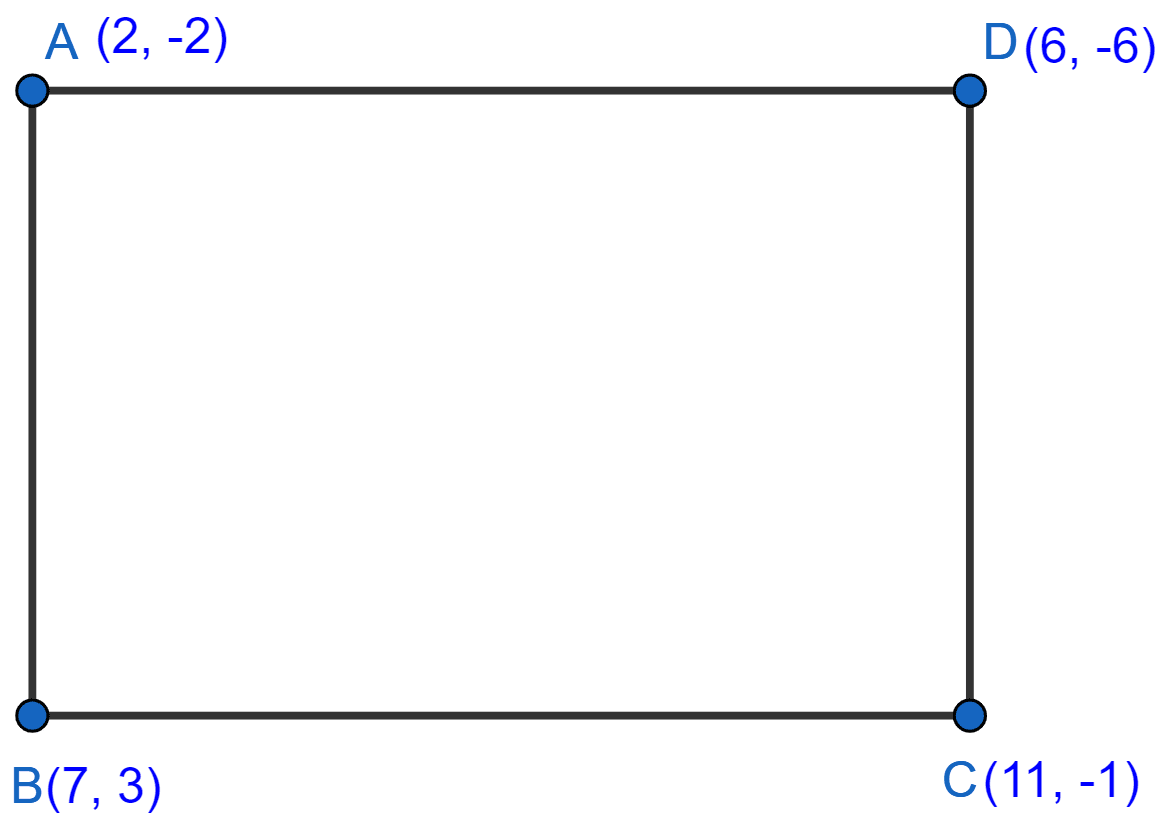
By distance formula,
Hence,
AB = CD and BC = AD
Since, opposite sides are equal,
Hence, proved that ABCD is a rectangle.
Find the coordinates of the centre of the circle passing through the three given points A(5, 1), B(-3, -7) and C(7, -1).
Answer
Let O(x, y) be the coordinates of the centre of the circle. Points A(5, 1), B(-3, -7), and C(7, -1) are on the circle.

By distance formula,
d =
As, OA = OB [∵ Both are radius of the same circle]
On squaring both sides,
As, OC = OB [∵ Both are radius of the same circle]
On squaring both sides,
Substituting value of x in above equation from equation 1 :
⇒ 5(-2 - y) + 3y = -2
⇒ -10 - 5y + 3y = -2
⇒ -2y = -2 + 10
⇒ -2y = 8
⇒ y = -4.
⇒ x = -2 - y = -2 - (-4) = -2 + 4 = 2.
C = (x, y) = (2, -4).
Hence, the coordinates of the centre of the circle are (2, -4).