Statistics

Find the mean of 8, 6, 10, 12, 1, 3, 4, 4.

Answer

Mean (M) = $\dfrac{\text{Sum of the all observations}}{\text{No. of observation}}$

Sum of all observations = 8 + 6 + 10 + 12 + 1 + 3 + 4 + 4 = 48.

$M = \dfrac{48}{8} = 6.$

Hence, mean = 6.

5 people were asked about the time in a week they spend in doing social work in their community. They replied 10, 7, 13, 20 and 15 hours, respectively. Find the mean time in a week devoted by them for social work.

Answer

Mean (M) = $\dfrac{\text{Total social work hrs}}{\text{No. of people}}$

Sum of hours spent by people on social work = 10 + 7 + 13 + 20 + 15 = 65.

$M = \dfrac{65}{5} = 13.$

Hence, the mean time in a week devoted by people for social work is 13 hours.

The enrollment of a school during six consecutive years was as follows:

1620, 2060, 2540, 3250, 3500, 3710.

Find the mean enrollment.

Answer

Mean (M) = $\dfrac{\text{Sum of enrollments}}{\text{No. of years}}$

Sum of enrollments = 1620 + 2060 + 2540 + 3250 + 3500 + 3710 = 16680

$M = \dfrac{16680}{6} = 2780.$

Hence, the mean enrollment = 2780.

Find the mean of the first twelve natural numbers.

Answer

Mean (M) = $\dfrac{\text{Sum of first 12 natural nos.}}{\text{No. of natural nos.}}$

Sum of first 12 natural numbers = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = 78.

$M = \dfrac{78}{12} = 6.5$

Hence, the mean of the first twelve natural numbers = 6.5

Find the mean of the first six prime numbers.

Answer

First six prime numbers = 2, 3, 5, 7, 11, 13.

Mean (M) = $\dfrac{\text{Sum of prime numbers}}{\text{No. of prime numbers}}$

Sum of prime numbers = 2 + 3 + 5 + 7 + 11 + 13 = 41.

$M = \dfrac{41}{6}$.

Hence, the mean of the first six prime numbers = $\dfrac{41}{6}$.

Find the mean of the first seven odd prime numbers.

Answer

First seven odd prime numbers = 3, 5, 7, 11, 13, 17, 19.

Mean (M) = $\dfrac{\text{Sum of first seven odd prime nos.}}{\text{No. of prime nos.}}$

Sum of first seven odd prime numbers = 3 + 5 + 7 + 11 + 13 + 17 + 19 = 75.

$M = \dfrac{75}{7} \\[1em] = 10\dfrac{5}{7}.$

Hence, the mean of the first seven odd prime numbers = $10\dfrac{5}{7}$.

The marks (out of 100) obtained by a group of students in a Mathematics test are 81, 72, 90, 90, 85, 86, 70, 93 and 71. Find the mean marks obtained by the group of students.

Answer

Mean marks (M) = $\dfrac{\text{Total marks}}{\text{No. of students}}$

Total marks = 81 + 72 + 90 + 90 + 85 + 86 + 70 + 93 + 71 = 738.

$M = \dfrac{738}{9} = 82.$

Hence, mean marks = 82.

The mean of the age of three students Vijay, Rahul and Rakhi is 15 years. If their ages are in the ratio 4 : 5 : 6 respectively, then find their ages.

Answer

Let age of Vijay, Rahul and Rakhi be 4x, 5x and 6x respectively..

Mean age = $\dfrac{\text{Sum of age of students}}{\text{No. of students}}$

Sum of age of students = 4x + 5x + 6x = 15x.

$\therefore 15 = \dfrac{15x}{3} \\[1em] \Rightarrow 15 \times 3 = 15x \\[1em] \Rightarrow x = \dfrac{15 \times 3}{15} \\[1em] \Rightarrow x = 3.$

Vijay's age = 4x = 4 × 3 = 12 years,

Rahul's age = 5x = 5 × 3 = 15 years,

Rakhi's age = 6x = 6 × 3 = 18 years.

Hence, age of three students Vijay, Rahul and Rakhi are 12, 15 and 18 years respectively.

The mean of 5 numbers is 20. If one number is excluded, mean of the remaining numbers becomes 23. Find the excluded number.

Answer

Given, mean of 5 numbers = 20.

By formula,

Mean = $\dfrac{\text{Total sum of observations}}{\text{No. of observations}}$

$\therefore 20 = \dfrac{\text{Total sum of observations}}{5} \\[1em] \text{Total sum of observations} = 20 \times 5 = 100.$

Let number excluded be x.

Given, Mean of the remaining numbers becomes 23.

$\therefore 23 = \dfrac{100 - x}{4} \\[1em] \Rightarrow 23 \times 4 = 100 - x \\[1em] \Rightarrow 92 = 100 - x \\[1em] \Rightarrow x = 100 - 92 \\[1em] \Rightarrow x = 8.$

Hence, excluded number = 8.

The mean of 25 observations is 27. If one observation is included, the mean still remains 27. Find the included observation.

Answer

Given,

The mean of 25 observations is 27.

By formula,

Mean = $\dfrac{\text{Total sum of observations}}{\text{No. of observations}}$

$\therefore 27 = \dfrac{\text{Total sum of observations}}{25} \\[1em] \text{Total sum of observations} = 27 \times 25 = 675.$

Given, mean after including new number remains 27.

No. of observations = 25 + 1 = 26.

$\therefore 27 = \dfrac{\text{New sum of observations}}{26} \\[1em] \text{New sum of observations} = 27 \times 26 = 702.$

New number included = New sum of observations - Total sum of observations = 702 - 675 = 27.

Hence, the new included observation = 27.

The mean of 5 observations is 15. If the mean of first three observations is 14 and that of the last three is 17, find the third observation.

Answer

By formula,

Mean = $\dfrac{\text{Total sum of observations}}{\text{No. of observations}}$

Given,

The mean of 5 observations = 15

$\therefore 15 = \dfrac{\text{Total sum of 5 observations}}{5} \\[1em] \Rightarrow \text{Total sum of observations} = 15 \times 5 \\[1em] \Rightarrow \text{Total sum of observations} = 75.$

Given,

Mean of first 3 observations = 14

$\therefore 14 = \dfrac{\text{Sum of first 3 observations}}{3} \\[1em] \Rightarrow \text{Sum of first three observations} = 14 \times 3 \\[1em] \Rightarrow \text{Sum of first three observations} = 42.$

Given,

Mean of last 3 observations = 17

$\therefore 17 = \dfrac{\text{Sum of last 3 observations}}{3} \\[1em] \Rightarrow \text{Sum of last three observations} = 17 \times 3 \\[1em] \Rightarrow \text{Sum of last three observations} = 51.$

Third observation = Sum of first three observations + Sum of last three observations - Total sum of observation
= 51 + 42 - 75 = 18.

Hence, the third observation = 18.

The mean of 8 variates is 10.5. If seven of them are 3, 15, 7, 19, 2, 17 and 8, then find the 8th variate.

Answer

By formula,

Mean = $\dfrac{\text{Sum of observations}}{\text{No. of observations}}$

Given,

Mean of 8 variates = 10.5

$\therefore 10.5 = \dfrac{\text{Sum of eight variates}}{8} \\[1em] \text{Sum of 8 variates} = 10.5 \times 8 = 84.$

Given,

Seven variates = 3, 15, 7, 19, 2, 17 and 8.

Sum of seven variates = (3 + 15 + 7 + 19 + 2 + 17 + 8) = 71.

8th variate = Sum of 8 variates - Sum of 7 variates = 84 - 71 = 13.

Hence, 8th variate = 13.

The mean weight of 8 students is 45.5 kg. Two more students having weights 41.7 kg and 53.3 kg join the group. What is the new mean weight?

Answer

By formula,

Mean = $\dfrac{\text{Total weight of students}}{\text{No. of students}}$

Given,

$\therefore 45.5 = \dfrac{\text{Total weight of eight students}}{8} \\[1em] \text{Total weight of eight students} = 45.5 \times 8 = 364.$

Weight of two more students are 41.7 kg and 53.3 kg

Now,

The total weight of 10 students = 364 + 41.7 + 53.3 = 459 kg.

New mean weight = $\dfrac{459}{10}$ = 45.9 kg.

Hence, new mean weight = 45.9 kg.

Mean of 9 observations was found to be 35. Later on, it was detected that an observation 81 was misread as 18. Find the correct mean of the observations.

Answer

By formula,

Mean = $\dfrac{\text{Total sum of observations}}{\text{No. of observations}}$

$\therefore 35 = \dfrac{\text{Total sum of observations}}{9} \\[1em] \text{Total sum of observations} = 35 \times 9 = 315.$

Since, 81 was misread as 18.

So, Actual sum of observation = Total sum of observations - 18 + 81 = 315 - 18 + 81 = 378.

Correct mean = $\dfrac{378}{9}$ = 42.

Hence, the correct mean = 42.

A student scored the following marks in 11 questions of a question paper:

7, 3, 4, 1, 5, 8, 2, 2, 5, 7, 6.

Find the median marks.

Answer

Given,

Marks scored in 11 questions of a question paper by the student are:

7, 3, 4, 1, 5, 8, 2, 2, 5, 7, 6

Arranging it in ascending order, we have

1, 2, 2, 3, 4, 5, 5, 6, 7, 7, 8

Here, n = 11 which is odd.

∴ Median = $\dfrac{(n + 1)}{2}$ th term

= $\dfrac{11 + 1}{2} = \dfrac{12}{2}$ = 6th term.

6th term = 5.

Hence, median marks = 5.

Calculate the mean and the median of the numbers:

2, 3, 4, 3, 0, 5, 1, 1, 3, 2.

Answer

By formula,

$\text{Mean } = \dfrac{\text{Sum of numbers}}{\text{No. of numbers}}$

Sum of numbers = 0 + 1 + 1 + 2 + 2 + 3 + 3 + 3 + 4 + 5 = 24

$\therefore \text{Mean } = \dfrac{24}{10} \\[1em] = 2.4$

Given,

Numbers : 2, 3, 4, 3, 0, 5, 1, 1, 3, 2.

First arrange the numbers in ascending order :

0, 1, 1, 2, 2, 3, 3, 3, 4, 5

Here, n = 10 which is even.

By formula,

$\text{Median} = \dfrac{\dfrac{n}{2}\text{ th observation} + \Big(\dfrac{n}{2} + 1\Big) \text{ th observation}}{2} \\[1em] = \dfrac{\dfrac{10}{2}\text{ th observation} + \Big(\dfrac{10}{2} + 1\Big)\text{ th observation}}{2} \\[1em] = \dfrac{5 \text{ th observation} + 6\text{ th observation}}{2} \\[1em] = \dfrac{2 + 3}{2} \\[1em] = \dfrac{5}{2} \\[1em] = 2.5$

Hence, mean = 2.4 and median = 2.5

A group of students was given a special test in Mathematics. The test was completed by the various students in the following time in (minutes) :

24, 30, 28, 17, 22, 36, 30, 19, 32, 18, 20, 24.

Find the mean time and median time taken by the students to complete the test.

Answer

By formula,

$\text{Mean} = \dfrac{\text{Total minutes}}{\text{No. of students}} \\[1em] = \dfrac{24 + 30 + 28 + 17 + 22 + 36 + 30 + 19 + 32 + 18 + 20 + 24}{12} \\[1em] = \dfrac{300}{12} \\[1em] = 25.$

Arranging the data in ascending order :

17, 18, 19, 20, 22, 24, 24, 28, 30, 30, 32, 36

Here, n = 12 which is even

By formula,

$\text{Median} = \dfrac{\dfrac{n}{2}\text{ th observation} + \Big(\dfrac{n}{2} + 1\Big) \text{ th observation}}{2} \\[1em] = \dfrac{\dfrac{12}{2}\text{ th observation} + \Big(\dfrac{12}{2} + 1\Big)\text{ th observation}}{2} \\[1em] = \dfrac{6 \text{ th observation} + 7\text{ th observation}}{2} \\[1em] = \dfrac{24 + 24}{2} \\[1em] = \dfrac{48}{2} \\[1em] = 24$

Hence, mean time = 25 minutes and median time = 24 minutes.

In a Science test given to a group of students, the marks scored by them (out of 100) are

41, 39, 52, 48, 54, 62, 46, 52, 40, 96, 42, 40, 98, 60, 52.

Find the mean and median of this data.

Answer

By formula,

$\text{Mean} = \dfrac{\text{Total marks}}{\text{No. of students}}$

Total marks = 41 + 39 + 52 + 48 + 54 + 62 + 46 + 52 + 40 + 96 + 42 + 40 + 98 + 60 + 52
= 822

$\text{Mean} = \dfrac{822}{15} \\[1em] = 54.8$

Given,

Student's marks : 41, 39, 52, 48, 54, 62, 46, 52, 40, 96, 42, 40, 98, 60, 52.

On arranging the marks obtained by the students in ascending order, we have :

39, 40, 40, 41, 42, 46, 48, 52, 52, 52, 54, 60, 62, 96, 98

Here, n = 15 which is odd.

By formula,

$\text{Median } = \dfrac{n + 1}{2} \text{ th observation} \\[1em] = \dfrac{15 + 1}{2} \text{ th observation} \\[1em] = \dfrac{16}{2} \text{ th observation} \\[1em] = 8 \text{ th observation} \\[1em] = 52.$

Hence, mean = 54.8 and median = 52.

The points scored by a Kabaddi team in a series of matches are as follows:

7, 17, 2, 5, 27, 15, 8, 14, 10, 48, 10, 7, 24, 8, 28, 18.

Find the mean and the median of the points scored by the Kabaddi team.

Answer

Given,

Points scored by kabaddi team : 7, 17, 2, 5, 27, 15, 8, 14, 10, 48, 10, 7, 24, 8, 28, 18.

By formula,

$\text{Mean} = \dfrac{\text{Sum of points}}{\text{No. of matches}} \\[1em] = \dfrac{7 + 17 + 2 + 5 + 27+ 15 + 8 + 14 + 10 + 48 + 10 + 7 + 24 + 8 + 28 + 18}{16} \\[1em] = \dfrac{248}{16} \\[1em] = 15.5$

Let’s arrange the given data in ascending order:

2, 5, 7, 7, 8, 8, 10, 10, 14, 15, 17, 18, 24, 27, 28, 48.

Here, n = 16 when is even

By formula,

$\text{Median} = \dfrac{\dfrac{n}{2}\text{ th observation} + \Big(\dfrac{n}{2} + 1\Big) \text{ th observation}}{2} \\[1em] = \dfrac{\dfrac{16}{2}\text{ th observation} + \Big(\dfrac{16}{2} + 1\Big)\text{ th observation}}{2} \\[1em] = \dfrac{8 \text{ th observation} + 9\text{ th observation}}{2} \\[1em] = \dfrac{10 + 14}{2} \\[1em] = \dfrac{24}{2} \\[1em] = 12$

Hence, the mean and the median of the points scored by the Kabaddi team are 15.5 and 12 respectively.

The following observations have been arranged in ascending order. If the median of the data is 47.5, find the value of x.

17, 21, 23, 29, 39, 40, x, 50, 51, 54, 59, 67, 91, 93.

Answer

Given data,

17, 21, 23, 29, 39, 40, x, 50, 51, 54, 59, 67, 91, 93.

Here, n = 14 which is even.

By formula,

$\text{Median} = \dfrac{\dfrac{n}{2}\text{ th observation} + \Big(\dfrac{n}{2} + 1\Big) \text{ th observation}}{2} \\[1em] = \dfrac{\dfrac{14}{2}\text{ th observation} + \Big(\dfrac{14}{2} + 1\Big)\text{ th observation}}{2} \\[1em] = \dfrac{7 \text{ th observation} + 8\text{ th observation}}{2} \\[1em] = \dfrac{x + 50}{2}.$

Given, median = 47.5

⇒ $\dfrac{x + 50}{2}$ = 47.5

⇒ x + 50 = 95

⇒ x = 95 - 50

⇒ x = 45.

Hence, the value of x is 45.

The following observations have been arranged in ascending order. If the median of the data is 13, find the value of x.

3, 6, 7, 10, x, x + 4, 19, 20, 25, 28.

Answer

Given observations in ascending order :

3, 6, 7, 10, x, x + 4, 19, 20, 25, 28

Here, n = 10 which is even.

By formula,

$\text{Median} = \dfrac{\dfrac{n}{2}\text{ th observation} + \Big(\dfrac{n}{2} + 1\Big) \text{ th observation}}{2} \\[1em] = \dfrac{\dfrac{10}{2}\text{ th observation} + \Big(\dfrac{10}{2} + 1\Big)\text{ th observation}}{2} \\[1em] = \dfrac{5 \text{ th observation} + 6\text{ th observation}}{2} \\[1em] = \dfrac{x + x + 4}{2} \\[1em] = \dfrac{2x + 4}{2} \\[1em] = x + 2.$

Given, median = 13

⇒ x + 2 = 13

⇒ x = 13 - 2

⇒ x = 11.

Hence, the value of x is 11.

State which of the following variables are continuous and which are discrete:

(i) marks scored (out of 50) in a test.

(ii) daily temperature of your city.

(iii) sizes of shoes.

(iv) distance travelled by a man.

(v) time.

Answer

(i) Discrete

(ii) Continuous

(iii) Discrete

(iv) Continuous

(v) Continuous

Using class intervals 0-4, 5-9, 10-14, ....... construct the frequency distribution for the following data :

13, 6, 10, 5, 11, 14, 2, 8, 15, 16, 9, 13, 17, 11, 19, 5, 7, 12, 20, 21, 18, 1, 8, 12, 18.

Answer

The frequency distribution table for given grouped data is :

Given below are the marks obtained by 27 students in a test:

21, 3, 28, 38, 6, 40, 20, 26, 9, 8, 14, 18, 20, 16, 17, 10, 8, 5, 22, 27, 34, 2, 35, 31, 16, 28, 37.

(i) Using the class intervals 1-10, 11-20 etc. construct a frequency table.

(ii) State the range of these marks.

(iii) State the class mark of the third class of your frequency table.

Answer

(i) The frequency distribution table for given grouped data is :

(ii) Range = Highest mark - Lowest mark = 40 - 2 = 38.

Hence, range of marks = 38.

(iii) Class mark = $\dfrac{\text{Lower limit + Upper limit}}{2}$

Third class of frequency table = 21-30.

Substituting values we get :

Class mark = $\dfrac{21 + 30}{2} = \dfrac{51}{2}$ = 25.5

Hence, class mark = 25.5

Explain the meaning of the following terms:

(i) variate

(ii) class size

(iii) class mark

(iv) class limits

(v) true class limits

(vi) frequency of a class

(vii) cumulative frequency of a class.

Answer

(i) Variant — A particular value of a variable is called variate.

(ii) Class size — The difference between the actual upper limit and the actual lower limit of a class is called its class size.

(iii) Class mark — The class mark of a class is the value midway between its actual lower limit and actual upper limit.

(iv) Class limits — In the frequency table the class interval is called class limits.

(v) True class limits — In a continuous distribution, the class limits are called true or actual class limits.

(vi) Frequency of a class — The number of tally marks opposite to a variate is its frequency and it is written in the next column opposite to tally marks of the variate.

(vii) Cumulative frequency of a class — The sum of frequency of all previous classes and that particular class is called the cumulative frequency of the class.

Fill in the blanks :

(i) The number of observations in a particular class is called .......... of the class.

(ii) The difference between the class marks of two consecutive classes is the .......... of the class.

(iii) The range of the data 16, 19, 23, 13, 11, 25, 18 is .......... .

(iv) The mid-point of the class interval is called its .......... .

(v) The class mark of the class 4 – 9 is .......... .

Answer

(i) The number of observations in a particular class is called frequency of the class.

(ii) The difference between the class marks of two consecutive classes is the size of the class.

(iii) Range = Highest value - Lowest value

= 25 - 11 = 14.

The range of the data 16, 19, 23, 13, 11, 25, 18 is 14.

(iv) The mid-point of the class interval is called its class marks.

(v) Class mark = $\dfrac{4 + 9}{2} = \dfrac{13}{2}$ = 6.5

The class mark of the class 4 – 9 is 6.5.

The marks obtained (out of 50) by 40 students in a test are given below:

28, 31, 45, 03, 05, 18, 35, 46, 49, 17, 10, 28, 31, 36, 40, 44, 47, 13, 19, 25, 24, 31, 38, 32, 27, 19, 25, 28, 48, 15, 18, 31, 37, 46, 06, 01, 20, 10, 45, 02.

(i) Taking class intervals 1 – 10, 11 – 20, .., construct a tally chart and a frequency distribution table.

(ii) Convert the above distribution to continuous distribution.

(iii) State the true class limits of the third class.

(iv) State the class mark of the fourth class.

Answer

(i) The frequency distribution table for given grouped data is :

(ii) Adjustment factor = (Lower limit of one class - Upper limit of previous class) / 2

$= \dfrac{11 - 10}{2} = \dfrac{1}{2}$ = 0.5

Subtracting the adjustment factor (0.5) from all the lower limits and add the adjustment factor (0.5) to all the upper limits.

Continuous frequency distribution for the given data is :

(iii) Third class : 20.5 - 30.5

Hence, lower limit : 20.5 and upper limit : 30.5

(iv) Class mark = $\dfrac{\text{Lower limit + Upper limit}}{2}$

= $\dfrac{30.5 + 40.5}{2} = \dfrac{71}{2}$ = 35.5

Hence, class mark of fourth class = 35.5

Use the adjoining table to find:

(i) upper and lower limits of fifth class.

(ii) true class limits of the fifth class.

(iii) class boundaries of the third class.

(iv) class mark of the fourth class.

(v) width of sixth class.

Answer

(i) Fifth class : 48 - 52

Hence, upper limit = 52 and lower limit = 48.

(ii) Adjustment factor = (Lower limit of class - Upper limit of previous class) / 2

= $\dfrac{48 - 47}{2} = \dfrac{1}{2}$ = 0.5

True lower limit = 48 - 0.5 = 47.5

True upper limit = 52 + 0.5 = 52.5

Hence, true class limits of fifth class = 47.5 and 52.5

(iii) Third class : 38 - 42

True lower limit = 38 - 0.5 = 37.5

True upper limit = 42 + 0.5 = 42.5

Hence, class boundaries of third class = 37.5 and 42.5

(iv) Fourth class : 43 - 47

Class mark = $\dfrac{\text{Lower class limit + Upper class limit}}{2}$

= $\dfrac{43 + 47}{2} = \dfrac{90}{2}$

= 45.

Hence, class mark of fourth class = 45.

(v) Fifth class : 53 - 57

True lower limit = 53 - 0.5 = 52.5

True upper limit = 57 + 0.5 = 57.5

Hence, width = 5.

The marks of 200 students in a test were recorded as follows :

Draw the cumulative frequency table.

Answer

The cumulative frequency table is shown below :

Given below are the marks secured by 35 students in a test:

41, 32, 35, 21, 11, 47, 42, 00, 05, 18, 25, 24, 29, 38, 30, 04, 14, 24, 34, 44, 48, 33, 36, 38, 41, 46, 08, 34, 39, 11, 13, 27, 26, 43, 03.

Taking class intervals 0 - 10, 10 - 20, 20 - 30 ...., construct frequency as well as cumulative frequency distribution table. Find the number of students obtaining below 20 marks.

Answer

The cumulative frequency distribution table is given below:

From table,

The no. of students obtaining below 20 marks = 10.

The marks out of 100 of 50 students in a test are given below:

5 35 6 35 18 36 12 36 85 32

20 36 22 38 24 50 22 39 74 31

25 54 25 64 25 70 28 66 58 25

29 72 31 82 31 84 31 82 37 21

32 84 32 92 35 95 34 92 35 5

(i) Taking a class interval of size 10, construct a frequency as well as cumulative frequency table for the given data.

(ii) Which class has the largest frequency?

(iii) How many students score less than 40 marks?

(iv) How many students score first division (60% or more) marks?

Answer

(i) The cumulative frequency table for given data is :

(ii) From table,

Class 30 - 40 has the largest frequency distribution table.

(iii) From table,

34 students score less than 40 marks.

(iv) Total marks = 100

60% marks = $\dfrac{60}{100} \times 100$ = 60.

From tables, students scoring less than 60 = 37

Total students = 50.

Students scoring more than 60% = 50 - 37 = 13.

Hence, 13 students scored more than 60% marks.

Construct the frequency distribution table from the following data :

State the number of children in the age group 10 - 13.

Answer

The frequency distribution table for given data is :

From table,

Frequency of class 10 - 13 = 73.

Hence, the no. of children in the age group 10 - 13 are 73.

Rewrite the following cumulative frequency distribution into frequency distribution:

Less than or equal to 10 = 2

Less than or equal to 20 = 7

Less than or equal to 30 = 18

Less than or equal to 40 = 32

Less than or equal to 50 = 43

Less than or equal to 60 = 50

Answer

The frequency distribution table for given data is :

The maximum temperatures (in degree celsius) for Delhi for the month of April, 2014, as reported by the Meteorological Department, are given below:

27.4, 28.3, 23.9, 23.6, 25.4, 27.5, 28.1, 28.4, 30.5, 29.7, 30.6, 31.7, 32.2, 32.6, 33.4, 35.7, 36.1, 37.2, 38.4, 40.1, 40.2, 40.5, 41.1, 42.0, 42.1, 42.3, 42.4, 42.9, 43.1, 43.2.

Construct a frequency distribution table.

Answer

Here, maximum = 43.2 and minimum = 23.6.

Range = 43.2 - 23.6 = 19.6

Let us form 5 classes of each size 4.

Since, we want to score 43.2 in last class and 43.5 is the upper limit of the last class, so the lower limit of first class is 23.5

The frequency distribution table of the given data is as follows :

The class marks of a distribution are 94, 104, 114, 124, 134, 144 and 154. Determine the class size and the class limits of the fourth class.

Answer

Class size = Difference between two successive class marks = 104 - 94 = 10.

Class mark of fourth class = 124.

Lower limit of class = Class mark - (Class size/2)

= 124 - $\dfrac{10}{2}$

= 124 - 5

= 119.

Upper class limit = Class mark + (Class size/2)

= 124 + $\dfrac{10}{2}$

= 124 + 5

= 129.

Hence, class size = 10, lower limit = 119 and upper limit = 129.

The class marks of a distribution are 9.5, 16.5, 23.5, 30.5, 37.5 and 44.5. Determine the class size and the class limits of the third class.

Answer

Class size = Difference between two successive class marks = 16.5 - 9.5 = 7.

Class mark of third class = 23.5

Lower limit of class = Class mark - (Class size/2)

= 23.5 - $\dfrac{7}{2}$

= 23.5 - 3.5

= 20.

Upper class limit = Class mark + (Class size/2)

= 23.5 + $\dfrac{7}{2}$

= 23.5 + 3.5

= 27.

Hence, class size = 7, lower limit = 20 and upper limit = 27.

The area under wheat cultivation last year in the following states, correct to the nearest lacs hectares was :

Represent the above information by a bar graph.

Answer

Steps of construction :

1. Take states along x-axis.

2. Take 1 cm along y-axis = 20 lac hectares.

3. Construct rectangles corresponding to the above distribution table.

The required bar graph is shown in the adjoining figure.

The number of books sold by a shopkeeper in a certain week was as follows :

Draw a bar graph for the above data.

Answer

Steps of construction :

1. Take days along x-axis.

2. Take 1 cm along y-axis = 50 books.

3. Construct rectangles corresponding to the above distribution table.

The required bar graph is shown in the adjoining figure.

Given below is the data of percentage of passes of a certain school in the ICSE for consecutive years :

Draw a bar graph to represent the above data.

Answer

Steps of construction :

1. Take year along x-axis.

2. Take 1 cm along y-axis = 10 %.

3. Construct rectangles corresponding to the above distribution table.

The required bar graph is shown in the adjoining figure.

Birth rate per thousand of different countries over a period is :

Draw a horizontal bar graph to represent the above data.

Answer

Steps of construction :

1. Take country along y-axis.

2. Take birth rate along x-axis.

3. Construct rectangles corresponding to the above distribution table.

The required bar graph is shown in the adjoining figure.

Given below is the data of number of students (boys and girls) in class IX of a certain school :

Draw a bar graph to represent the above data.

Answer

Steps of construction :

1. Take class along x-axis.

2. Take 1 cm along y-axis = 5 students.

3. Construct rectangles corresponding to the above distribution table.

The required bar graph is shown in the adjoining figure.

Draw a histogram to represent the following data :

Answer

Steps of construction of histogram :

1. Take 2 cm along x-axis = 10 marks.

2. Take 1 cm along y-axis = 1 student.

3. Construct rectangles corresponding to the above continuous frequency distribution table.

The required histogram is shown in the adjoining figure.

Draw a histogram to represent the following frequency distribution of monthly wages of 255 workers of a factory.

Answer

Steps of construction of histogram :

1. Since the scale on x-axis starts at 850, a kink is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 850.

2. Take 2 cm along x-axis = 100 rupees.

3. Take 1 cm along y-axis = 10 workers.

4. Construct rectangles corresponding to the above continuous frequency distribution table.

The required histogram is shown in the adjoining figure.

Draw a histogram for the following data :

Answer

We know that class mark is the mid-point of class. So, frequency distribution table for above data is :

Steps of construction of histogram :

1. Since the scale on x-axis starts at 10, a kink is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 10.

2. Take 2 cm along x-axis = 5 units.

3. Take 1 cm along y-axis = 5 units.

4. Construct rectangles corresponding to the above continuous frequency distribution table.

The required histogram is shown in the adjoining figure.

Draw a histogram for the following frequency distribution :

Answer

Frequency distribution table for above data is :

Steps of construction of histogram :

1. Take 2 cm along x-axis = 2 years.

2. Take 1 cm along y-axis = 3 children.

3. Construct rectangles corresponding to the above continuous frequency distribution table.

The required histogram is shown in the adjoining figure.

Draw a histogram for the following data :

Answer

The following frequency distribution is discontinuous, to convert it into continuous frequency distribution,

Adjustment factor = (Lower limit of one class - Upper limit of previous class) / 2

= $\dfrac{66 - 65}{2} = \dfrac{1}{2}$

= 0.5

Subtract the adjustment factor (0.5) from all the lower limits and add the adjustment factor (0.5) to all the upper limits.

Continuous frequency distribution for given data is :

Steps of construction of histogram :

1. Since, the scale on x-axis starts at 58.5, a break (kink) is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 58.5

2. Take 2 cm along x-axis = 7 units.

3. Take 1 cm along y-axis = 5 units.

4. Construct rectangles corresponding to the above continuous frequency distribution table.

The required histogram is shown in the adjoining figure.

Draw a frequency polygon for the following data :

Answer

Frequency distribution table :

Steps to draw frequency polygon :

1. Since, the scale on x-axis starts at 30, a kink is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 30.

2. Take 1 cm along x-axis = 10 units.

3. Take 1 cm along y-axis = 5 units.

4. Find the mid-points of class-intervals.

5. Find points corresponding to given frequencies of classes and the mid-points of class-intervals, and plot them.

6. Join consecutive points by line segments.

7. Join first end point with mid-point of class 30 - 40 with zero frequency and join the other end with mid-point of class 100 - 110 with zero frequency.

The required frequency polygon is shown below:

In a class of 60 students, the marks obtained in a monthly test were as under :

Answer

Frequency distribution table :

Steps to draw frequency polygon :

1. Take 2 cm along x-axis = 10 marks.

2. Take 1 cm along y-axis = 5 students.

3. Find the mid-points of class-intervals.

4. Find points corresponding to given frequencies of classes and the mid-points of class-intervals, and plot them.

5. Join consecutive points by line segments.

6. Join first end point with mid-point of class 0 - 10 with zero frequency and join the other end with mid-point of class 60 - 70 with zero frequency.

The required frequency polygon is shown below:

In a class of 90 students, the marks obtained in a weekly test were as under :

Draw a frequency polygon for the above data.

Answer

The following frequency distribution is discontinuous, to convert it into continuous frequency distribution,

Adjustment factor = (Lower limit of one class - Upper limit of previous class) / 2

= $\dfrac{21 - 20}{2} = \dfrac{1}{2}$

= 0.5

Subtract the adjustment factor (0.5) from all the lower limits and add the adjustment factor (0.5) to all the upper limits.

Continuous frequency distribution for given data is :

Steps to draw frequency polygon :

1. Since, the scale on x-axis starts at 10.5, a kink is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 10.5.

2. Take 1 cm along x-axis = 5 marks.

3. Take 1 cm along y-axis = 5 students.

4. Find the mid-points of class-intervals.

5. Find points corresponding to given frequencies of classes and the mid-points of class-intervals, and plot them.

6. Join consecutive points by line segments.

7. Join first end point with mid-point of class 10.5 - 15.5 with zero frequency and join the other end with mid-point of class 50.5 - 55.5 with zero frequency.

The required frequency polygon is shown alongside.

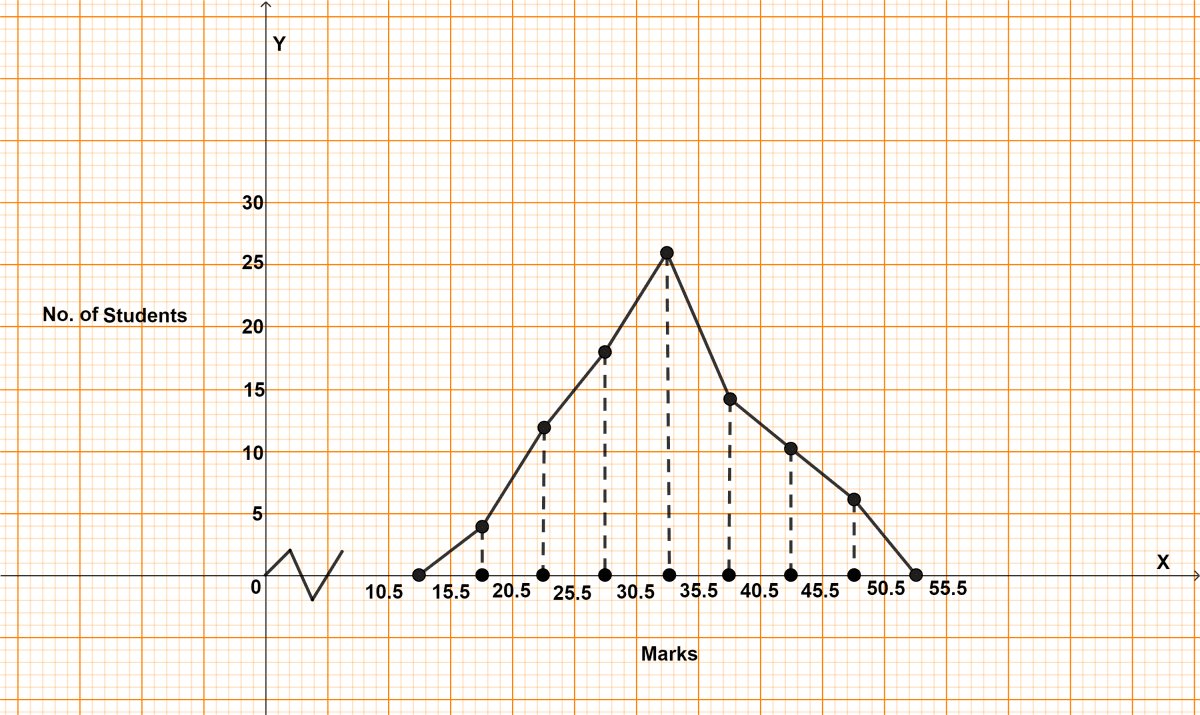
In a city, the weekly observations made in a study on the cost of living index are given in the following table :

Draw a frequency polygon for the data given above.

Answer

Frequency distribution table :

Steps to draw frequency polygon :

1. Since, the scale on x-axis starts at 130, a kink is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 130.

2. Take 2 cm along x-axis = 10 units (cost of living index).

3. Take 2 cm along y-axis = 5 weeks.

4. Find the mid-points of class-intervals.

5. Find points corresponding to given frequencies of classes and the mid-points of class-intervals, and plot them.

6. Join consecutive points by line segments.

7. Join first end point with mid-point of class 130 - 140 with zero frequency and join the other end with mid-point of class 200 - 210 with zero frequency.

The required frequency polygon is shown alongside.

Construct a combined histogram and frequency polygon for the following data :

Answer

Frequency distribution table :

Steps of construction of histogram :

1. Since, the scale on x-axis starts at 135, a break (kink) is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 135.

2. Take 2 cm along x-axis = 15 rupees.

3. Take 2 cm along y-axis = 5 workers.

4. Construct rectangles corresponding to the above continuous frequency distribution table.

The required histogram is shown in the adjoining figure.

Steps of construction of frequency polygon :

1. Mark the mid-points of upper bases of rectangles of the histogram.

2. Join the consecutive mid-points by line segments.

3. Join the first end point with the mid-point of class 135 - 150 with zero frequency, and join the other end point with the mid-point of class 240 - 255 with zero frequency.

The required frequency polygon is shown by thick line segments in the diagram.

In a study of diabetic patients, the following data was obtained :

Represent the above data by a histogram and a frequency polygon.

Answer

Frequency distribution table :

Steps of construction of histogram :

1. Take 1 cm along x-axis = 10 years.

2. Take 1 cm along y-axis = 6 patients.

3. Construct rectangles corresponding to the above continuous frequency distribution table.

The required histogram is shown in the adjoining figure.

Steps of construction of frequency polygon :

1. Mark the mid-points of upper bases of rectangles of the histogram.

2. Join the consecutive mid-points by line segments.

3. Join the first end point with the mid-point of class 0 - 10 with zero frequency, and join the other end point with the mid-point of class 80 - 90 with zero frequency.

The required frequency polygon is shown by thick line segments in the diagram.

The water bills (in rupees) of 32 houses in a locality are given below:

30, 48, 52, 78, 103, 85, 37, 94, 72, 73, 66, 52, 92, 65, 78, 81, 64, 60, 75, 78, 108, 63, 71, 54, 59, 75, 100, 103, 35, 89, 95, 73.

Taking class intervals 30 - 40, 40 - 50, 50 - 60, ......, form frequency distribution table.

Construct a combined histogram and frequency polygon.

Answer

First represent the given data in the form of a frequency distribution table.

Here, class intervals represent water bills class and frequency represents no. of houses.

Steps of construction of histogram :

1. Take 1 cm along x-axis = 10 units.

2. Take 1 cm along y-axis = 1 unit.

3. Construct rectangles corresponding to the above continuous frequency distribution table.

The required histogram is shown in the adjoining figure.

Steps of construction of frequency polygon :

1. Mark the mid-points of upper bases of rectangles of the histogram.

2. Join the consecutive mid-points by line segments.

3. Join the first end point with the mid-point of class 20 - 30 with zero frequency, and join the other end point with the mid-point of class 110 - 120 with zero frequency.

The required frequency polygon is shown by thick line segments in the diagram.

The number of matchsticks in 40 boxes on counting was found as given below:

44, 41, 42, 43, 47, 50, 51, 49, 43, 42, 40, 42, 44, 45, 49, 42, 46, 49, 45, 49, 45, 47, 48, 43, 43, 44, 48, 43, 46, 50, 43, 52, 46, 49, 52, 51, 47, 43, 43, 45.

Taking classes 40 - 42, 42 - 44 ......, construct the frequency distribution table for the above data. Also draw a combined histogram and frequency polygon to represent the distribution.

Answer

First represent the given data in a frequency distribution table as shown below:

Steps of construction of histogram :

1. Since, the scale on x-axis starts at 38, a kink is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 38.

2. Take 1 cm along x-axis = 2 units.

3. Take 1 cm along y-axis = 2 units.

4. Construct rectangles corresponding to the above continuous frequency distribution table.

The required histogram is shown in the adjoining figure.

Steps of construction of frequency polygon :

1. Mark the mid-points of upper bases of rectangles of the histogram.

2. Join the consecutive mid-points by line segments.

3. Join the first end point with the mid-point of class 38 - 40 with zero frequency, and join the other end point with the mid-point of class 54 - 56 with zero frequency.

The required frequency polygon is shown by thick line segments in the diagram.

The histogram showing the weekly wages (in rupees) of workers in a factory is given alongside.

Answer the following about the frequency distribution:

(i) What is the frequency of the class 400 - 425?

(ii) What is the class having minimum frequency?

(iii) What is the cumulative frequency of the class 425 – 450?

(iv) Construct a frequency and cumulative frequency table for the given distribution.

Answer

(i) From graph,

The frequency of class 400 - 425 is 18.

(ii) From graph,

Minimum frequency of a class = 4.

Hence, the class having minimum frequency is 475 - 500.

(iii) Cumulative frequency of class 425 - 450 = Sum of frequency of class 425 - 450 and previous classes

= 10 + 18 + 6 = 34.

Hence, cumulative frequency of class 425 - 450 = 34.

(iv) The cumulative frequency distribution table for given distribution is shown below :

Marks scored by students of class 10A and 10B in a particular class test are as follows:

Draw their frequency polygons on the same graph.

Answer

The following frequency distribution is discontinuous, to convert it into continuous frequency distribution,

Adjustment factor = $\dfrac{\text{(Lower limit of one class - Upper limit of previous class)}}{2}$

= $\dfrac{\text{(6 - 5)}}{2} = \dfrac{1}{2} = 0.5$

Subtract the adjustment factor (0.5) from all the lower limits and add the adjustment factor (0.5) to all the upper limits.

Continuous frequency distribution for given data is :

Steps to draw frequency polygon :

1. Take 1 cm along x-axis = 4 units.

2. Take 1 cm along y-axis = 1 units.

3. Find the mid-points of class-intervals.

4. Find points corresponding to given frequencies of classes and the mid-points of class-intervals, and plot them.

5. Join consecutive points by line segments.

6. Join first end point with mid-point of class -5.5 - 0.5 with zero frequency and join the other end with mid-point of class 40.5 - 45.5 with zero frequency.

The required frequency polygon is shown alongside.

The marks obtained by 17 students in a mathematics test (out of 100) are given below :

91, 82, 100, 100, 96, 65, 82, 76, 79, 90, 46, 64, 72, 66, 68, 48, 49

The range of data is

1. 46

2. 54

3. 90

4. 100

Answer

Range = Upper limit - Lower limit = 100 - 46 = 54.

Hence, Option 2 is the correct option.

The class mark of the class 90 - 120 is

1. 90

2. 105

3. 115

4. 120

Answer

Class mark = $\dfrac{\text{Upper limit + Lower limit}}{2}$

= $\dfrac{90 + 120}{2} = \dfrac{210}{2}$

= 105.

Hence, Option 2 is the correct option.

In a frequency distribution, the mid-value of a class is 10 and the width of the class is 6. The lower limit of the class is

1. 6

2. 7

3. 8

4. 12

Answer

Lower limit of class = Mid value - $\dfrac{\text{Width}}{2}$

= 10 - $\dfrac{6}{2}$

= 10 - 3

= 7.

Hence, Option 2 is the correct option.

The width of each of 5 continuous classes in a frequency distribution is 5 and the lower limit of the lowest class is 10. The upper limit of the highest class is

1. 15

2. 25

3. 35

4. 40

Answer

Let x and y be the upper and lower class limit of frequency distribution.

Given,

Width of class = 5

∴ x - y = 5

⇒ x - 10 = 5

⇒ x = 5 + 10 = 15.

Upper class limit of highest class = No. of continuous class × Width + Lower class limit of lowest class

= 5 × 5 + 10

= 25 + 10

= 35.

Hence, Option 3 is the correct option.

The class marks of a frequency distribution are given as follows :

15, 20, 25, .........

The class corresponding to the class mark 20 is

1. 12.5 - 17.5

2. 17.5 - 22.5

3. 18.5 - 21.5

4. 19.5 - 20.5

Answer

As the class marks are 15, 20, 25, ......... which are at equal gaps, so the classes are of equal size.

∴ size of class = difference between two consecutive class marks
= 20 - 15 = 5.

Half of class size = $\dfrac{5}{2}$ = 2.5

∴ Lower limit of class corresponding to the class mark 20 = class mark - half of class size
= 20 - 2.5 = 17.5

∴ Upper limit of class corresponding to the class mark 20 = class mark + half of class size
= 20 + 2.5 = 22.5

∴ Class corresponding to the class mark 20 is 17.5 - 22.5

Hence, Option 2 is the correct option.

In the class intervals 10 - 20, 20 - 30, the number 20 is included in

1. 10 - 20

2. 20 - 30

3. both the intervals

4. none of these intervals

Answer

The number 20 will be included in 20 - 30 interval.

Hence, Option 2 is the correct option.

A grouped frequency distribution table with class intervals of equal size using 250 - 270 (270 not included in this interval) as one of the class intervals is constructed for the following data :

268, 220, 368, 258, 242, 310, 272, 342, 310, 290, 300, 320, 319, 304, 402, 318, 406, 292, 354, 278, 210, 240, 330, 316, 406, 215, 258, 236.

The frequency of class 310 - 330 is

1. 4

2. 5

3. 6

4. 7

Answer

Elements from above data in the class 310 - 330 are :

310, 310, 320, 319, 318, 316.

Hence, the frequency of class 310 - 330 is 6.

Hence, Option 3 is the correct option.

The mean of x - 1, x + 1, x + 3 and x + 5 is

1. x + 1

2. x + 2

3. x + 3

4. x + 4

Answer

By formula,

$\text{Mean } = \dfrac{\text{Sum of observations}}{\text{No. of observations}}$

Sum of observations = (x - 1) + (x + 1) + (x + 3) + (x + 5) = 4x + 8.

$\text{Mean } = \dfrac{4x + 8}{4} \\[1em] = \dfrac{4(x + 2)}{4} \\[1em] = x + 2.$

Hence, Option 2 is the correct option.

The mean of five numbers is 30. If one number is excluded, their mean becomes 28. The excluded number is

1. 28

2. 30

3. 35

4. 38

Answer

By formula,

$\text{Mean } = \dfrac{\text{Sum of observations}}{\text{No. of observations}} \\[1em] 30 = \dfrac{\text{Sum of observations}}{5} \\[1em] \text{Sum of observations} = 150$

Let excluded number be x.

Given, on excluding x the mean is 28.

$\therefore \dfrac{150 - x}{4} = 28 \\[1em] \Rightarrow 150 - x = 112 \\[1em] \Rightarrow x = 150 - 112 \\[1em] \Rightarrow x = 38.$

Hence, Option 4 is the correct option.

If the mean of x₁, x₂ is 7.5, and the mean of x₁, x₂, x₃ is 8, then the value of x₃ is

1. 9

2. 8

3. 7.5

4. 6

Answer

By formula,

$\text{Mean} = \dfrac{\text{Sum of observations}}{\text{No. of observations}}$

Given, Mean of x₁, x₂ = 7.5

$\therefore 7.5 = \dfrac{x_1 + x_2}{2} \\[1em] \Rightarrow x_1 + x_2 = 15 ...........(i)$

Given, Mean of x₁, x₂ and x₃ = 8

$\therefore 8 = \dfrac{x_1 + x_2 + x_3}{3} \\[1em] \Rightarrow x_1 + x_2 + x_3 = 24 ...........(ii)$

Subtracting equation (i) from (ii), we get :

⇒ x₁ + x₂ + x₃ - (x₁ + x₂) = 24 - 15

⇒ x₁ - x₁ + x₂ - x₂ + x₃ = 9

⇒ x₃ = 9.

Hence, Option 1 is the correct option.

If each observation of the data is increased by 5, then their mean

1. remains the same

2. becomes 5 times the original mean

3. is decreased by 5

4. is increased by 5

Answer

Let x₁, x₂, x₃ be the observations.

So, their mean (M) = $\dfrac{x_1 + x_2 + x_3}{3}$

Since, each observations is increased by 5, so observations will be

x₁ + 5, x₂ + 5, x₃ + 5.

$\text{Mean (M}_1) = \dfrac{x_1 + 5 + x_2 + 5 + x_3 + 5}{3} \\[1em] = \dfrac{x_1 + x_2 + x_3 + 15}{3} \\[1em] = \dfrac{x_1 + x_2 + x_3}{3} + \dfrac{15}{3} \\[1em] = \dfrac{x_1 + x_2 + x_3}{3} + 5.$

So, M₁ = M + 5.

Hence, Option 4 is the correct option.

The mean of 100 observations is 50. If one of the observation which was 50 is replaced by 150, the resulting mean will be

1. 50.5

2. 51

3. 51.5

4. 52

Answer

By formula,

Mean = $\dfrac{\text{Sum of observations}}{\text{No. of observations}}$

Given,

Mean of 100 observations is 50.

$\therefore 50 = \dfrac{\text{Sum of observations}}{100} \\[1em] \text{Sum of observations} = 50 \times 100 = 5000.$

Since, observation which was 50 is replaced by 150.

So,

Sum of observation = 5000 - 50 + 150 = 5100.

New mean = $\dfrac{5100}{100}$ = 51.

Hence, Option 2 is the correct option.

For drawing a frequency polygon of a continuous frequency distribution, we plot the points whose ordinates are the frequencies of the respective classes and abscissae are respectively :

1. upper limits of the classes

2. lower limits of the classes

3. class marks of the classes

4. upper limits of preceding classes

Answer

We know, class marks are the mean of lower and upper limit of the class intervals.

Hence, Option 3 is the correct option.

Median of the numbers 4, 4, 5, 7, 6, 7, 7, 3, 12 is

1. 4

2. 5

3. 6

4. 7

Answer

Arranging given data in ascending order :

3, 4, 4, 5, 6, 7, 7, 7, 12.

No. of observation (n) = 9.

Here, n is odd.

By formula,

$\text{Median} = \dfrac{(n + 1)}{2} \text{th observation} \\[1em] = \dfrac{9 + 1}{2} \text{th observation} \\[1em] = \dfrac{10}{2} \text{th observation} \\[1em] = 5 \text{th observation} \\[1em] = 6.$

Hence, Option 3 is the correct option.

The median of the data

78, 56, 22, 34, 45, 54, 39, 68, 54, 84 is

1. 45

2. 49.5

3. 54

4. 56

Answer

Arranging given data in ascending order :

22, 34, 39, 45, 54, 54, 56, 68, 78, 84.

No. of observation (n) = 10.

Here, n is even.

By formula,

$\text{Median} = \dfrac{\dfrac{n}{2} \text{th observation} + \Big(\dfrac{n}{2} + 1\Big) \text{th observation}}{2} \\[1em] = \dfrac{\dfrac{10}{2} \text{th observation} + \Big(\dfrac{10}{2} + 1\Big) \text{th observation}}{2} \\[1em] = \dfrac{\text{5th observation + 6th observation}}{2} \\[1em] = \dfrac{54 + 54}{2} \\[1em] = \dfrac{108}{2} \\[1em] = 54.$

Hence, Option 3 is the correct option.

In a data, 10 numbers are arranged in ascending order. If the 8th entry is increased by 6, then the median increases by

1. 0

2. 2

3. 3

4. 6

Answer

Since, number of observations (n) = 10, which is even.

By formula,

$\text{Median} = \dfrac{\dfrac{n}{2} \text{th observation} + \Big(\dfrac{n}{2} + 1\Big) \text{th observation}}{2} \\[1em] = \dfrac{\dfrac{10}{2} \text{th observation} + \Big(\dfrac{10}{2} + 1\Big) \text{th observation}}{2} \\[1em] = \dfrac{\text{5th observation + 6th observation}}{2}$

Since, 5th and 6th observation is not changed at all, so there is no change in median.

Hence, Option 1 is the correct option.

Consider the following two statements.

Statement 1: A histogram consists of a set of adjacent rectangles whose bases are equal to class size, and heights are equal to class frequencies.

Statement 2: In a bar graph, the breadth of a rectangle has no significance, whereas in a histogram, the breadth of a rectangle is meaningful and it represents the class size.

Which of the following is valid?

1. Both the statements are true.

2. Both the statements are false.

3. Statement 1 is true, and Statement 2 is false.

4. Statement 1 is false, and Statement 2 is true.

Answer

In a histogram, there are no gaps between the bars, indicating the continuous nature of the data.

The width of each bar (its base) represents the class interval or class size.

The height of each bar represents the frequency (or count) of observations falling within that specific class interval.

∴ Statement 1 is true.

In a bar graph, the bars have arbitrary width and does not represent any numerical quantity.

∴ Statement 2 is true.

∴ Both the statements are true.

Hence, option 1 is correct option.

Assertion (A): Runs scored by batsman A are 55, 60, 30, 80 while runs scored by batsman B are 81, 87, 76, 92. Then B has higher range than A.

Reason (R): Range is the difference between maximum and minimum values of a variable.

1. Assertion (A) is true, Reason (R) is false.

2. Assertion (A) is false, Reason (R) is true.

3. Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).

4. Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).

Answer

Range = Maximum Value - Minimum Value.

∴ Reason (R) is true.

For Batsman A:

Runs: 55, 60, 30, 80

Minimum value (Min) = 30

Maximum value (Max) = 80

Range of A = Max − Min = 80 − 30 = 50.

For Batsman B:

Runs: 81, 87, 76, 92

Minimum value (Min) = 76

Maximum value (Max) = 92

Range of B = Max − Min = 92 − 76 = 16.

Thus, B does not have higher range than A.

∴ Assertion (A) is false.

∴ Assertion (A) is false, Reason (R) is true.

Hence, option 2 is the correct option.

Assertion (A): Mean of first 5 odd natural numbers is 5.

Reason (R): Mean is the middle value of a set of observations.

1. Assertion (A) is true, Reason (R) is false.

2. Assertion (A) is false, Reason (R) is true.

3. Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).

4. Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).

Answer

The first 5 odd natural numbers are: 1, 3, 5, 7, 9.

The mean (arithmetic average) is calculated as the sum of all observations divided by the number of observations.

Sum = 1 + 3 + 5 + 7 + 9 = 25

Number of observations = 5

Mean = $\dfrac{\text{Sum of observations}}{\text{Number of observations}} = \dfrac{25}{5}$ = 5

∴ Assertion (A) is true.

The mean is the arithmetic average (sum of values divided by the count).

The median is the middle value of a set of observations when they are arranged in ascending or descending order.

∴ Reason (R) is false.

∴ Assertion (A) is true, Reason (R) is false.

Hence, option 1 is the correct option.

Assertion (A): If 6 students score 78, 62, 91, 37, 80 and 66 marks in a subject, then median score is 72.

Reason (R): If number of observations is even, then

Median = $\dfrac{\dfrac{n}{2}\text{th observation} + \Big(\dfrac{n}{2} + 1\Big)\text{th observation}}{2}$, after putting all observations in ascending or descending order.

1. Assertion (A) is true, Reason (R) is false.

2. Assertion (A) is false, Reason (R) is true.

3. Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).

4. Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).

Answer

According to assertion: if 6 students score 78, 62, 91, 37, 80 and 66 marks in a subject, then median score is 72.

Arrange the scores in ascending order: 37, 62, 66, 78, 80, 91

There are 6 scores, so n = 6. This is an even number.

If number of observations is even, then

Median = $\dfrac{\dfrac{n}{2}\text{th observation} + \Big(\dfrac{n}{2} + 1\Big)\text{th observation}}{2}$, after putting all observations in ascending or descending order.

∴ Reason (R) is true.

Substituting the value,

$\text{Median }= \dfrac{\dfrac{6}{2}\text{th observation} + \Big(\dfrac{6}{2} + 1\Big)\text{th observation}}{2}\\[1em] = \dfrac{3\text{rd observation} + (3 + 1)\text{th observation}}{2}\\[1em] = \dfrac{3\text{th observation} + 4\text{th observation}}{2}\\[1em] = \dfrac{66 + 78}{2}\\[1em] = \dfrac{144}{2}\\[1em] = 72.$

∴ Assertion (A) is true.

∴ Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).

Hence, option 3 is the correct option.

Find the mean and the median of the following set of numbers :

8, 0, 5, 3, 2, 9, 1, 5, 4, 7, 2, 5.

Answer

By formula,

Mean = $\dfrac{\text{Sum of observations}}{\text{No. of observations}}$

Sum of observations = 8 + 0 + 5 + 3 + 2 + 9 + 1 + 5 + 4 + 7 + 2 + 5 = 51.

$\text{Mean} = \dfrac{51}{12} = 4.25$

By arranging data in ascending order, we get :

0, 1, 2, 2, 3, 4, 5, 5, 5, 7, 8, 9

Here, n = 12 which is even.

By formula,

Median = $\dfrac{\dfrac{n}{2}\text{th observation} + \Big(\dfrac{n}{2} + 1\Big)\text{th observation}}{2}$

Substituting the values we get,

$\text{Median} = \dfrac{\dfrac{12}{2}\text{th observation} + \Big(\dfrac{12}{2} + 1\Big)\text{th observation}}{2} \\[1em] = \dfrac{\text{6th observation + 7th observation}}{2} \\[1em] = \dfrac{4 + 5}{2} \\[1em] = \dfrac{9}{2} \\[1em] = 4.5$

Hence, mean = 4.25 and median = 4.5

Find the mean and the median of all the (positive) factors of 48.

Answer

Positive factors of 48 :

1, 2, 3, 4, 6, 8, 12, 16, 24, 48.

By formula,

$\text{Mean} = \dfrac{\text{Sum of positive factors of 48}}{\text{No. of factors}}$

Sum of positive factors of 48 = 1 + 2 + 3 + 4 + 6 + 8 + 12 + 16 + 24 + 48 = 124.

Mean $= \dfrac{124}{10} = 12.4$

Here, n = 10 which is even.

By formula,

Median = $\dfrac{\dfrac{n}{2}\text{th observation} + \Big(\dfrac{n}{2} + 1\Big)\text{th observation}}{2}$

Substituting the values we get,

$\text{Median} = \dfrac{\dfrac{10}{2}\text{th observation} + \Big(\dfrac{10}{2} + 1\Big)\text{th observation}}{2} \\[1em] = \dfrac{\text{5th observation + 6th observation}}{2} \\[1em] = \dfrac{6 + 8}{2} \\[1em] = \dfrac{14}{2} \\[1em] = 7$

Hence, mean = 12.4 and median = 7.

The mean weight of 60 students of a class is 52.75 kg. If the mean weight of 35 of them is 54 kg, find the mean weight of the remaining students.

Answer

By formula,

Mean = $\dfrac{\text{Sum of weight of students}}{\text{No. of students}}$

Given,

Mean weight of 60 students of a class = 52.75 kg

$\therefore 52.75 = \dfrac{\text{Total weight}}{60} \\[1em] \text{Total weight} = 60 \times 52.75 \\[1em] = 3165 \text{ kg}.$

Mean weight of 35 students among them = 54 kg.

So, the total weight of 35 students = 54 × 35 = 1890 kg.

Remaining students = 60 – 35 = 25

Total weight of 25 students = 3165 – 1890 = 1275 kg

Mean weight of 25 students = $\dfrac{1275}{25}$ = 51 kg.

Hence, the mean weight of the remaining students is 51 kg.

The mean age of 18 students of a class is 14.5 years. Two more students of age 15 years and 16 years join the class. What is the new mean age?

Answer

By formula,

$\text{Mean} = \dfrac{\text{Total age}}{\text{No. of students}} \\[1em] \therefore 14.5 = \dfrac{\text{Total age}}{18} \\[1em] \text{Total age} = 18 \times 14.5 = 261.$

Total age of 20 students = 261 + 15 + 16 = 292 years.

So, mean age of 20 students = $\dfrac{292}{20}$ = 14.6 years.

Hence, the new mean age is 14.6 years.

If the mean of the five observations x + 1, x + 3, x + 5, 2x + 2, 3x + 3 is 14, find the mean of first three observations.

Answer

By formula,

Mean = $\dfrac{\text{Sum of observations}}{\text{No. of observations}}$

Sum of observations = x + 1 + x + 3 + x + 5 + 2x + 2 + 3x + 3 = 8x + 14.

Given,

Mean of the five observations = 14.

$\Rightarrow \dfrac{8x + 14}{5} = 14 \\[1em] \Rightarrow 8x + 14 = 70 \\[1em] \Rightarrow 8x = 56 \\[1em] \Rightarrow x = \dfrac{56}{8} = 7.$

First three observations are

⇒ x + 1 = 7 + 1 = 8,

⇒ x + 3 = 7 + 3 = 10,

⇒ x + 5 = 7 + 5 = 12.

Mean = $\dfrac{8 + 10 + 12}{3} = \dfrac{30}{3}$ = 10.

Hence, the mean of first three observations is 10.

The mean height of 36 students of a class is 150.5 cm. Later on, it was detected that the height of one student was wrongly copied as 165 cm instead of 156 cm. Find the correct mean height.

Answer

By formula,

Mean = $\dfrac{\text{Total height}}{\text{No. of students}}$

Given,

Mean height of 36 students of a class = 150.5 cm

$\therefore 150.5 = \dfrac{\text{Total height}}{36} \\[1em] \text{Total height} = 150.5 \times 36 \\[1em] = 5418 \text{ cm}.$

As, height of one student was wrongly copied as 165 cm instead of 156 cm.

∴ Actual total height = 5418 – 165 + 156 = 5409 cm.

Actual Mean height = $\dfrac{5409}{36}$ = 150.25

Hence, the correct mean height is 150.25 cm.

The mean of 40 items is 35. Later on, it was discovered that two items were misread as 36 and 29 instead of 63 and 22. Find the correct mean.

Answer

By formula,

Mean = $\dfrac{\text{Sum of observations}}{\text{No. of observations}}$

Given,

Mean of 40 items = 35

$\therefore 35 = \dfrac{\text{Sum of observations}}{40} \\[1em] \text{Sum of observations} = 40 \times 35 = 1400.$

Since,

Sum of two items were misread as 36 and 29 instead of 63 and 22.

Actual sum of observation = 1400 - 36 - 29 + 63 + 22

= 1420.

Correct mean = $\dfrac{1420}{40}$ = 35.5

Hence, the correct mean is 35.5

The following observations have been arranged in ascending order. If the median of the data is 63, find the value of x.

29, 32, 48, 50, x, x + 2, 72, 75, 87, 91.

Answer

Here n = 10, which is even.

By formula,

$\text{Median} = \dfrac{\dfrac{n}{2}\text{th observation} + \Big(\dfrac{n}{2} + 1\Big)\text{th observation}}{2} \\[1em] \therefore 63 = \dfrac{\dfrac{10}{2}\text{th observation} + \Big(\dfrac{10}{2} + 1\Big)\text{th observation}}{2} \\[1em] \Rightarrow 126 = \text{5th observation + 6th observation} \\[1em] \Rightarrow 126 = x + x + 2 \\[1em] \Rightarrow 2x = 126 - 2 \\[1em] \Rightarrow 2x = 124 \\[1em] \Rightarrow x = 62.$

Hence, the value of x = 62.

Draw a histogram showing marks obtained by the students of a school in a Mathematics paper carrying 60 marks.

Answer

Steps of construction of histogram :

1. Take 2 cm along x-axis = 10 marks.

2. Take 1 cm along y-axis = 5 students.

3. Construct rectangles corresponding to the above continuous frequency distribution table.

The required histogram is shown in the adjoining figure.

In a class of 60 students, the marks obtained in a surprise test were as under :

Represent the above data by a histogram and a frequency polygon.

Answer

Steps of construction of histogram :

1. Since, the scale on x-axis starts at 8, a break (kink) is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 8.

2. Take 1 cm along x-axis = 10 marks.

3. Take 1 cm along y-axis = 5 students.

4. Construct rectangles corresponding to the above continuous frequency distribution table.

The required histogram is shown in the adjoining figure.

Steps of construction of frequency polygon :

1. Mark the mid-points of upper bases of rectangles of the histogram.

2. Join the consecutive mid-points by line segments.

3. Join the first end point with the mid-point of class 8 - 14 with zero frequency, and join the other end point with the mid-point of class 62 - 68 wirh zero frequency.

The required frequency polygon is shown by thick line segments in the diagram.

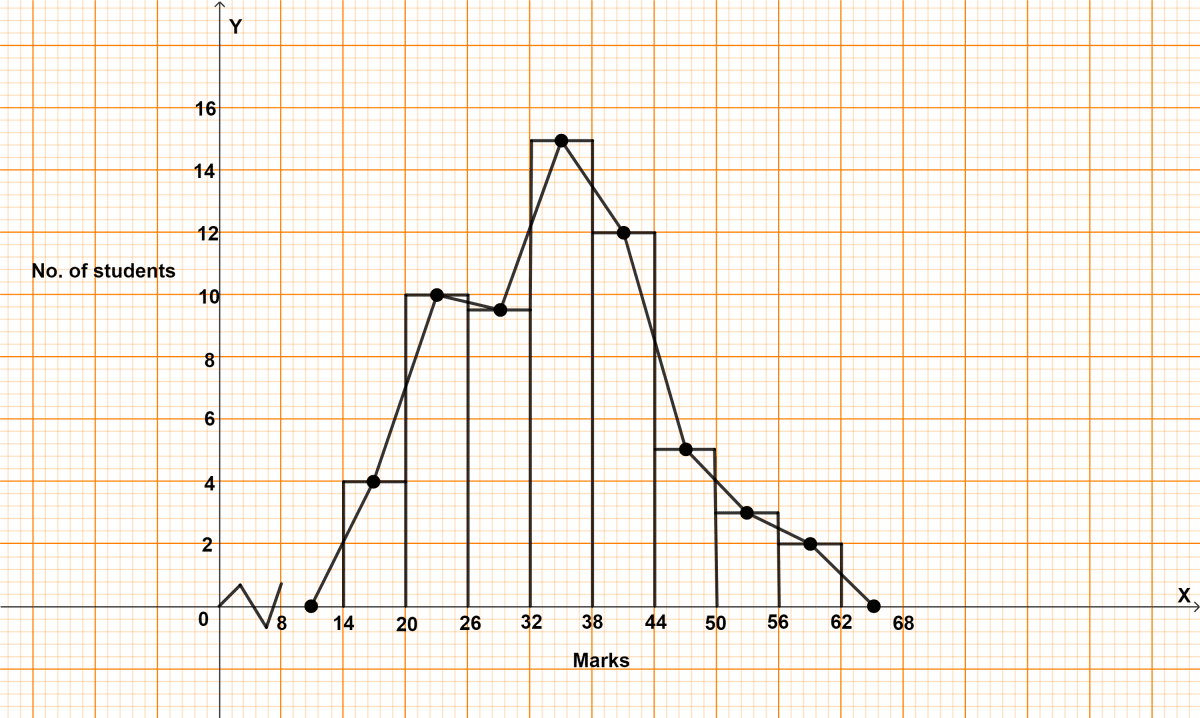
Construct a combined histogram and frequency polygon for the following distribution:

Answer

The following frequency distribution is discontinuous, to convert it into continuous frequency distribution,

Adjustment factor = (Lower limit of one class - Upper limit of previous class) / 2

= $\dfrac{101 - 100}{2} = \dfrac{1}{2}$

= 0.5

Subtract the adjustment factor (0.5) from all the lower limits and add the adjustment factor (0.5) to all the upper limits.

Continuous frequency distribution for given data is :

Steps of construction of histogram :

1. Since, the scale on x-axis starts at 80.5, a break (kink) is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 80.5

2. Take 1 cm along x-axis = 10 units.

3. Take 1 cm along y-axis = 5 units.

4. Construct rectangles corresponding to the above continuous frequency distribution table.

The required histogram is shown in the adjoining figure.

Steps of construction of frequency polygon :

1. Mark the mid-points of upper bases of rectangles of the histogram.

2. Join the consecutive mid-points by line segments.

3. Join the first end point with the mid-point of class 80.5 - 90.5 with zero frequency, and join the other end point with the mid-point of class 160.5 - 170.5 with zero frequency.

The required frequency polygon is shown by thick line segments in the diagram.

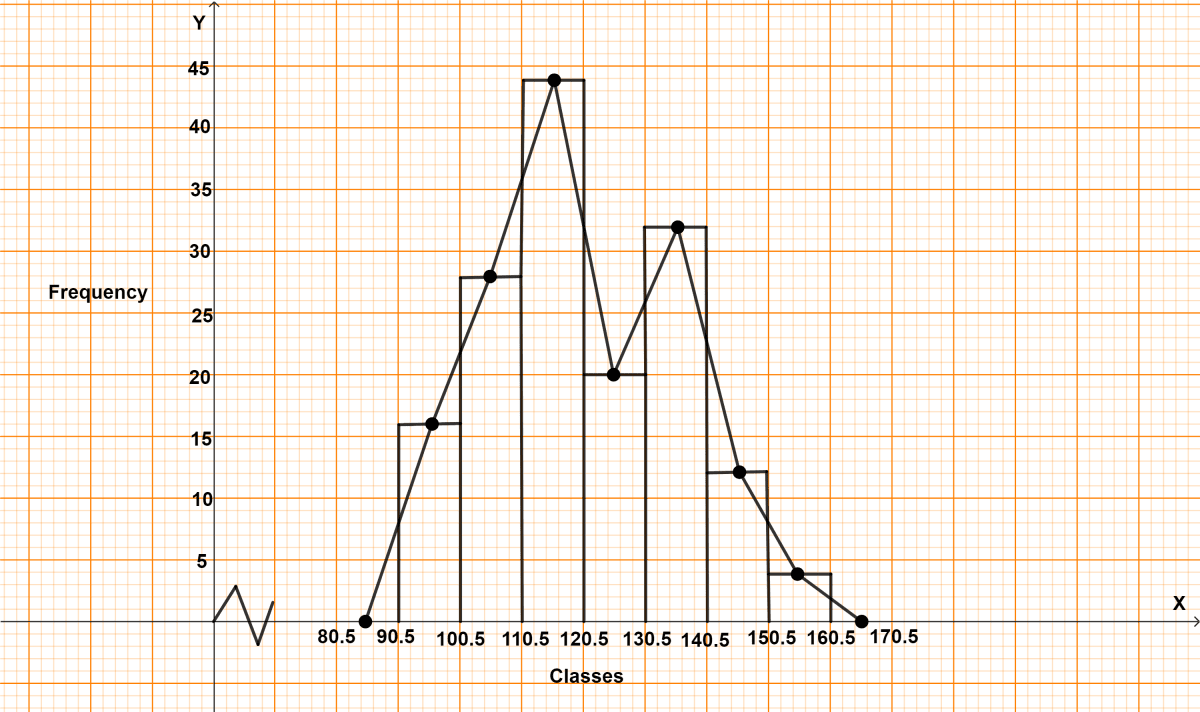
The Water bills (in rupees) of 40 houses in a locality are given below :

78 87 81 52 59 65 101 108 115 95

98 65 62 121 128 63 76 84 89 91

65 101 95 81 87 105 129 92 75 105

78 72 107 116 127 100 80 82 61 118

Form a frequency distribution table with a class size of 10. Also represent the above data with a histogram and frequency polygon.

Answer

From data,

Least term = 52 and Greatest term = 129.

Range = Greatest term - Least term = 129 – 52 = 77.

Construct a frequency distribution table:

Steps of construction of histogram :

1. Since, the scale on x-axis starts at 40, a break (kink) is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 40.

2. Take 1 cm along x-axis = 10 units.

3. Take 1 cm along y-axis = 2 units.

4. Construct rectangles corresponding to the above continuous frequency distribution table.

The required histogram is shown in the adjoining figure.

Steps of construction of frequency polygon :

1. Mark the mid-points of upper bases of rectangles of the histogram.

2. Join the consecutive mid-points by line segments.

3. Join the first end point with the mid-point of class 40 - 50 with zero frequency, and join the other end point with the mid-point of class 130 - 140 with zero frequency.

The required frequency polygon is shown by thick line segments in the diagram.

The data given below represent the marks obtained by 35 students:

21 26 21 20 23 24 22 19 24

26 25 23 26 29 21 24 19 25

26 25 22 23 23 27 26 24 25

30 25 23 28 28 24 28 28

Taking class intervals 19 - 20, 21 - 22 etc., make a frequency distribution for the above data.

Construct a combined histogram and frequency polygon for the distribution.

Answer

From above data :

Least mark = 19

Greatest marks = 30

Range = 30 – 19 = 11.

Given,

We need to take class intervals as 19 - 20, 21 - 22 etc.

The following frequency distribution is discontinuous, to convert it into continuous frequency distribution,

Adjustment factor = (Lower limit of one class - Upper limit of previous class) / 2

= $\dfrac{21 - 20}{2} = \dfrac{1}{2}$

= 0.5

Subtract the adjustment factor (0.5) from all the lower limits and add the adjustment factor (0.5) to all the upper limits.

Continuous frequency distribution for given data is :

Steps of construction of histogram :

1. Since, the scale on x-axis starts at 16.5, a break (kink) is shown near the origin on x-axis to indicate that the graph is drawn to scale beginning at 16.5.

2. Take 2 cm along x-axis = 2 units.

3. Take 1 cm along y-axis = 2 units.

4. Construct rectangles corresponding to the above continuous frequency distribution table.

The required histogram is shown in the adjoining figure.

Steps of construction of frequency polygon :

1. Mark the mid-points of upper bases of rectangles of the histogram.

2. Join the consecutive mid-points by line segments.

3. Join the first end point with the mid-point of class 16.5 - 18.5 with zero frequency, and join the other end point with the mid-point of class 30.5 - 32.5 with zero frequency.

The required frequency polygon is shown by thick line segments in the diagram.

The given histogram and frequency polygon shows the ages of teachers in a school. Answer the following:

(i) What is the class size of each class?

(ii) What is the class whose class mark is 48?

(iii) What is the class whose frequency is maximum?

(iv) Construct a frequency table for the given distribution.

Answer

(i) From graph,

Class marks of two successive class are 36 and 30.

Class size = 36 - 30 = 6.

Hence, the class size of each class is 6.

(ii) Lower limit of class = Class mark - $\dfrac{\text{Class size}}{2}$

= 48 - $\dfrac{6}{2}$

= 48 - 3

= 45.

Upper limit of class = Class mark + $\dfrac{\text{Class size}}{2}$

= 48 + $\dfrac{6}{2}$

= 48 + 3

= 51.

Hence, class whose class mark is 48 is 45 - 51.

(iii) From table,

Class with class mark = 54 has greatest frequency.

Lower limit of class = Class mark - $\dfrac{\text{Class size}}{2}$

= 54 - $\dfrac{6}{2}$

= 54 - 3

= 51.

Upper limit of class = Class mark + $\dfrac{\text{Class size}}{2}$

= 54 + $\dfrac{6}{2}$

= 54 + 3

= 57.

Hence, class 51 - 57 has highest frequency.

(iv) Frequency table for the given distribution :