Mathematics
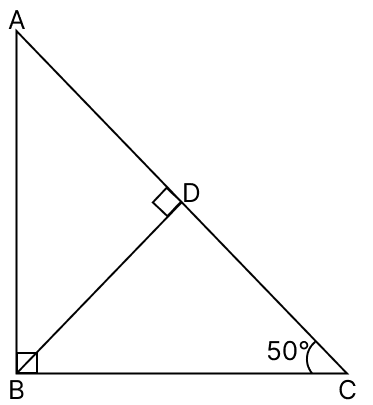
In the adjoining figure, ∠ABC = 90°, ∠BCA = 50° and BD ⊥ AC. Then ∠ABD =
30°
40°
50°
60°
Triangles
3 Likes
Answer
In △ABC,
By angle sum property of triangle,
⇒ ∠A + ∠B + ∠C = 180°
⇒ ∠A + 90° + 50° = 180°
⇒ ∠A + 140° = 180°
⇒ ∠A = 180° - 140°
⇒ ∠A = 40°.
In △ABD,
By angle sum property of triangle,
⇒ ∠A + ∠ABD + ∠D = 180°
⇒ 40° + ∠ABD + 90° = 180°
⇒ ∠ABD + 130° = 180°
⇒ ∠ABD = 180° - 130°
⇒ ∠ABD = 50°.
Hence, option 3 is the correct option.
Answered By
2 Likes
Related Questions
In a △ABC, AB = AC and ∠B = 50°. Then ∠A =
50°
80°
100°
105°
In a △PQR, ∠Q = 50°, ∠R = 65° and QR = 4 cm. Then PQ =
6 cm
5 cm
4 cm
3 cm
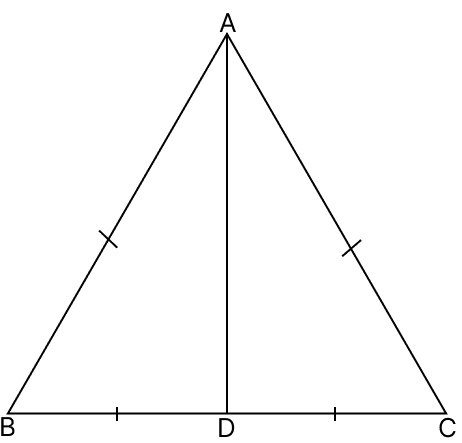
In the adjoining figure, AB = AC and BD = CD. Then, ∠ADC =
60°
75°
90°
100°
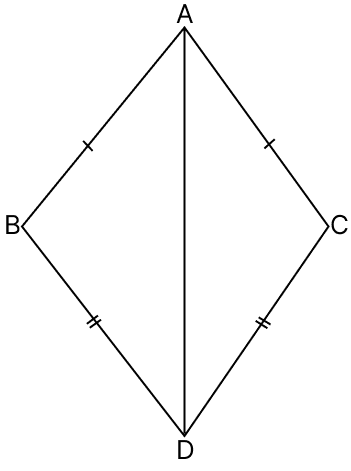
In the adjoining figure, AB = AC, BD = CD, ∠BAD = 32°, ∠BDC = 56°, ∠CAD = 2x° and ∠BDA = (x + y)°. The values of x and y will be :
x = 10, y = 16
x = 16, y = 12
x = 18, y = 8
x = 12, y = 16