Constructions

In a quadrilateral ABCD, side AB will be parallel to side DC, if :

1. ∠A + ∠B = 180°

2. ∠A = ∠B

3. ∠D = ∠C

4. ∠B + ∠C = 180°

Answer

In a quadrilateral ABCD, side AB will be parallel to side DC, if adjacent angles are supplementary.

⇒ ∠B + ∠C = 180°

⇒ ∠D + ∠A = 180°

Hence, option 4 is the correct option.

In which of the case, out of the following cases, it is not possible to construct a quadrilateral; when :

A. all the four sides are given.

B. one diagonal and all the four sides are given.

C. one angle and all the four sides are given.

D. both the diagonals and three sides are given.

1. A

2. B

3. C

4. D

Answer

It is not possible to construct a quadrilateral when all the four sides are given.

Hence, option 1 is the correct option.

In which of the case, out of the following cases, it is not possible to construct a parallelogram, when :

A. two adjacent sides and angle between them are given.

B. two adjacent sides and a diagonal are given.

C. both the diagonals are given.

D. both the diagonals and the angle between them are given.

1. A

2. B

3. C

4. D

Answer

It is not possible to construct a parallelogram, when both the diagonals are given.

Hence, option 3 is the correct option.

In which of the following cases, it is not possible to construct a rhombus when :

A. both the diagonals are given.

B. one side and one diagonal are given.

C. one side and one angle are given.

D. one diagonal is given.

1. A

2. B

3. C

4. D

Answer

It is not possible to construct a rhombus when one diagonal is given.

Hence, option 4 is the correct option.

In which of the following cases, it is not possible to construct a square when :

A. one diagonal is given

B. one side is given

C. one angle is given which is 90°

D. one side and the angle between a side and a diagonal are given.

1. A

2. B

3. C

4. D

Answer

It is not possible to construct a square when one angle is given which is 90°.

Hence, option 3 is the correct option.

Given below are the angles x and y.

Without measuring these angles, construct :

(i) ∠ABC = x + y

(ii) ∠ABC = 2x + y

(iii) ∠ABC = x + 2y

Answer

(i) Steps:

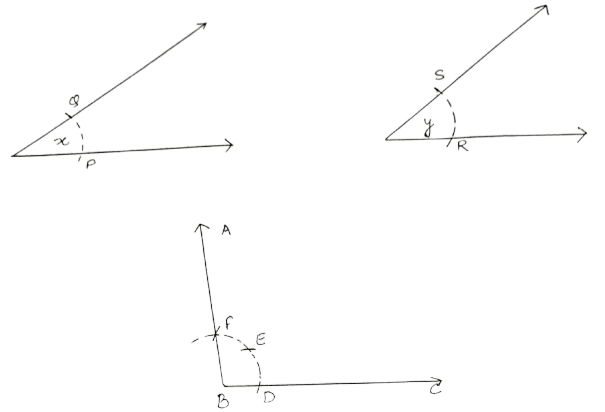
As shown above:

1. Draw line segment BC of any suitable length.

2. With B as centre, draw an arc of any suitable radius. With the same radius, draw arcs with the vertices of given angles as centres. Let these arcs cut arms of the angle x at the points P and Q, and arms of the angle y at points R and S.

3. From the arc, with centre B, cut DE = PQ = x and EF = SR = y.

4. Join BF and produce upto point A.

Hence, ∠ ABC = x + y.

(ii) Steps:

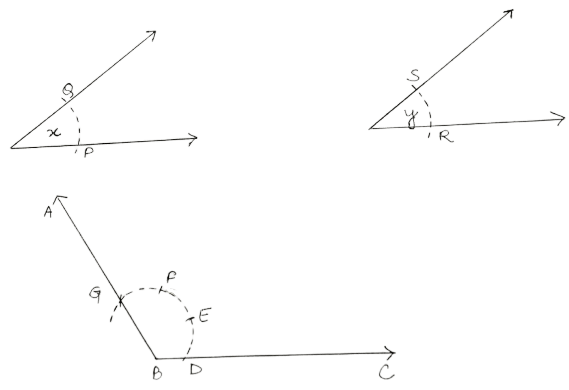
As shown above:

1. Draw line segment BC of any suitable length.

2. With B as centre, draw an arc of any suitable radius. With the same radius, draw arcs with the vertices of given angles as centres. Let these arcs cut arms of the angle x at the points P and Q, and arms of the angle y at the points R and S.

3. From the arc, with centre B, cut DE = PQ = x, EF = PQ = x and FG = RS = y.

4. Join BG and produce upto point A.

Hence, ∠ ABC = x + x + y = 2x + y.

(iii) Steps:

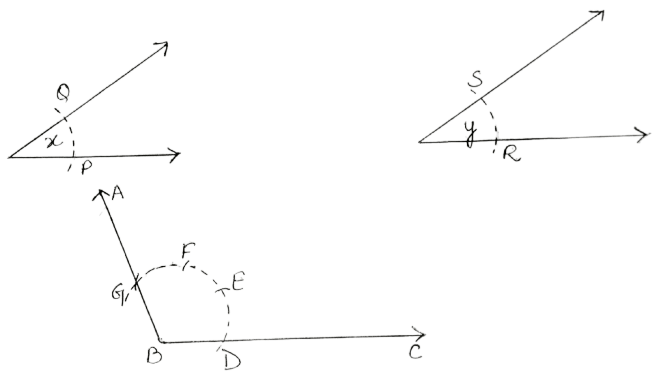
As shown above:

1. Draw line segment BC of any suitable length.

2. With B as centre, draw an arc of any suitable radius. With the same radius, draw arcs with the vertices of given angles as centres. Let these arcs cut arms of the angle x at the points P and Q, and arms of the angle y at the points R and S.

3. From the arc, with centre B, cut DE = PQ = x, EF = RS = y and FG = RS = y.

4. Join BG and produce upto point A.

Hence, ∠ ABC = x + y + y = x + 2y.

Draw angle ABC of any suitable measure.

(i) Draw BP, the bisector of angle ABC.

(ii) Draw BR, the bisector of angle PBC and draw BQ, the bisector of angle ABP.

(iii) Are the angles ABQ, QBP, PBR and RBC equal ?

(iv) Are the angles ABR and QBC equal ?

Answer

(i) Steps:

1. Draw an angle ABC.

2. With B as centre, draw an arc EF of any suitable radius.

3. With E as centre, draw an arc of same radius as taken in step 2.

4. With F as centre, draw an arc of same radius as taken in step 2 and cutting the previous arc at point G.

5. Join B and G and produce it till point P.

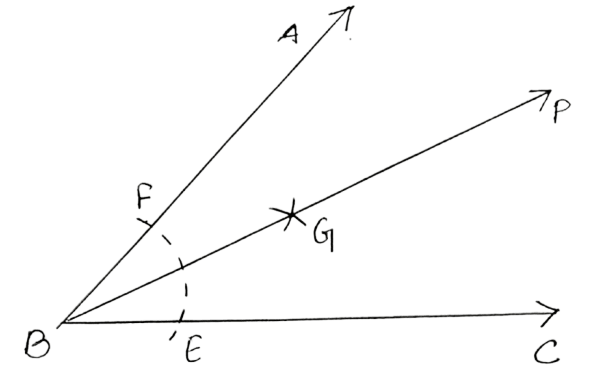
Hence, BP is angle bisector of angle ABC.

(ii) Steps:

1. Draw angle ABC and its angle bisector BP as explained in part i.

2. With B as center, draw an arc of any suitable radius which cuts AB at point G and BP at point F.

3. Taking G and F as centers, draw arcs of equal radii and let these arcs cut each other at point H. (The radii of these arcs must be more than half the distance between points G and F)

4. Join BH and produce upto point Q. BQ is the required bisector of ∠ABP. Thus, $∠\text{ABQ} = ∠\text{QBP} = \dfrac{∠\text{ABP}}{2}$.

5. With B as center, draw an arc of any suitable radius which cuts BP at point F and BC at point E.

6. Taking F and E as centers, draw arcs of equal radii and let these arcs cut each other at point I.
   (The radii of these arcs must be more than half the distance between points F and E)

7. Join BI and produce upto point R. BR is the required bisector of ∠PBC. Thus, $∠\text{RBP} = ∠\text{RBC} = \dfrac{∠\text{PBC}}{2}$.

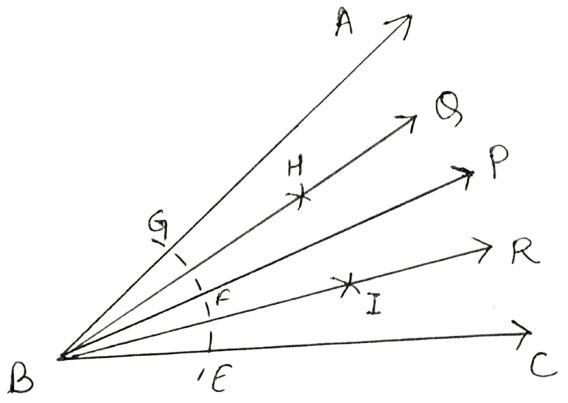
Hence, BR is angle bisector of angle PBC and BQ is angle bisectors of angle ABP.

(iii) $∠\text{ABQ} = ∠\text{QBP} = \dfrac{∠\text{ABP}}{2}$

$\phantom{(iii)}∠\text{PBR} = ∠\text{RBC} = \dfrac{∠\text{PBC}}{2}$

$\phantom{(iii)}∠\text{ABP} = ∠\text{PBC} \space [\because \text{BP bisects ∠\text{ABC}}]$

$\phantom{(iii)} \therefore ∠\text{ABQ} = ∠\text{QBP} = ∠\text{PBR} = ∠\text{RBC}$

(iv) ∠ABR = ∠ABQ + ∠QBP + ∠PBR
      ∠QBC = ∠QBP + ∠PBR + ∠RBC
      ∵ ∠RBC = ∠ABQ
      ∴ ∠QBC = ∠ABQ + ∠QBP + ∠PBR
      ∴ ∠ABR = ∠QBC

In each of the following, draw a perpendicular through point P to the line segment AB :

(i)

(ii)

(iii)

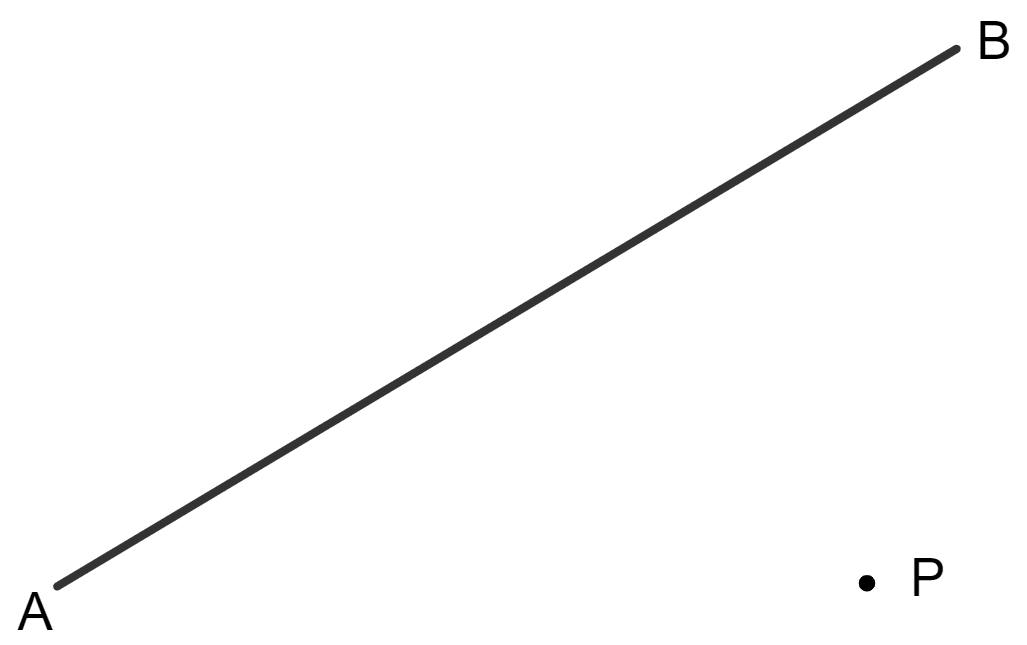
Answer

(i) Steps:

1. With P as center, draw an arc of a suitable radius which cuts AB at points C and D.

2. With C and D as centers, draw arcs of equal radii and let these arcs intersect each other at point Q.

(The radius of these arcs must be more than half of CD and both the arcs must be drawn on the other side.)

3. Join P and Q.

4. Let PQ cut AB at point O.

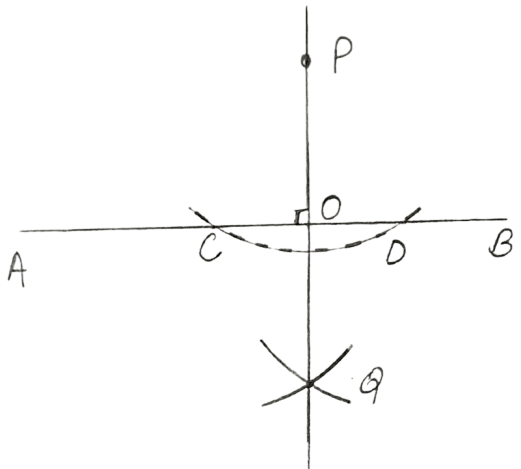
Clearly, ∠AOP = ∠BOP = 90°

Hence, OP is the required perpendicular.

(ii) Steps:

1. With P as center, draw an arc with a suitable radius which cuts AB at points C and D.

2. Taking C and D as centers, draw arcs of equal radii which cut each other at point O.

(The radius must be more than half the distance between C and D.)

3. Join P and O.

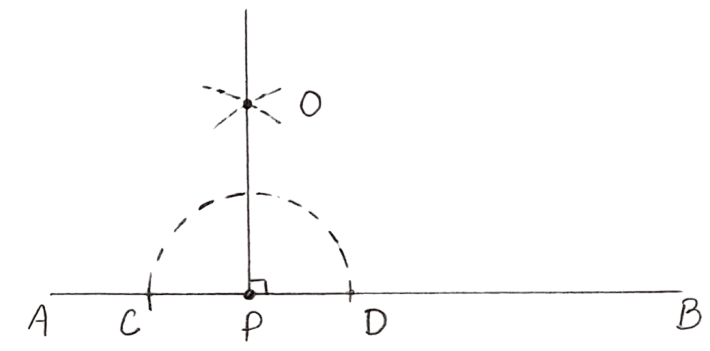
So, ∠OPA = ∠OPB = 90°.

Hence, OP is the required perpendicular.

(iii) Steps:

1. With P as center, draw an arc of a suitable radius which cuts AB at points C and D.

2. With C and D as centers, draw arcs of equal radii and let these arcs intersect each other at point Q.

(The radius of these arcs must be more than half of CD and both the arcs must be drawn on the other side.)

3. Join P and Q.

4. Let PQ cut AB at point O.

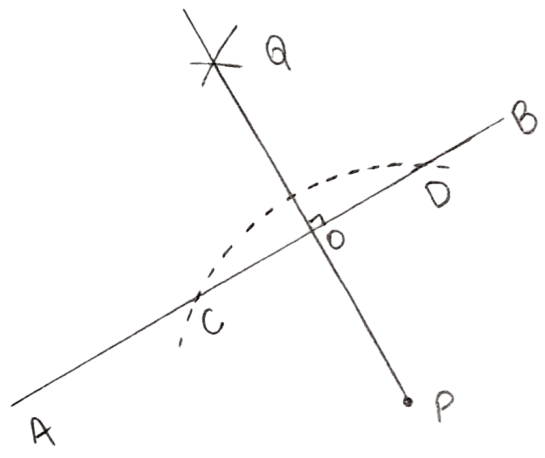
Clearly, ∠AOP = ∠BOP = 90°

Hence, OP is the required perpendicular.

Draw a line segment AB = 5.5 cm. Mark a point P, such that PA = 6 cm and PB = 4.8 cm. From the point P, draw a perpendicular to AB.

Answer

Steps:

1. Make a line AB = 5.5 cm.

2. With A as center and radius = 6 cm, draw an arc.

3. With B as center and radius = 4.8 cm, draw an arc which cut the previous arc at P.

4. Join AP and BP.

5. With P as center, draw an arc of a suitable radius which cuts AB at points C and D.

6. With C and D as centers, draw arcs of equal radii and let these arcs intersect each other at point E.

(The radius of these arcs must be more than half of CD and both the arcs must be drawn on the other side.)

7. Join P and E.

8. Let PE cut AB at point O.

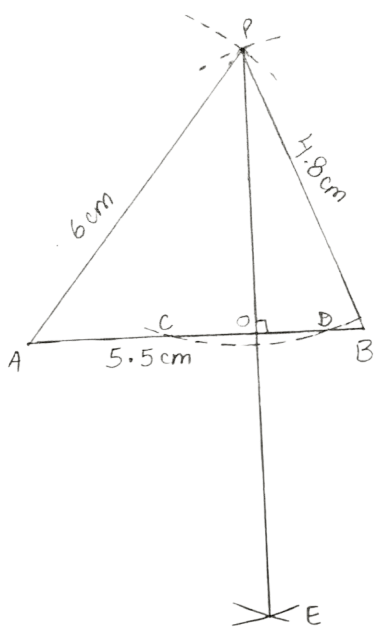
Clearly, ∠AOP = ∠BOP = 90°

Hence, OP is the required perpendicular.

Draw a line AB = 6 cm. Mark a point P any where outside the line AB. Through the point P, construct a line parallel to AB.

Answer

Steps:

1. Draw a line AB = 6cm.

2. Take any point Q in line AB and join it with the given point P.

3. At point P, construct ∠CPQ = ∠PQB.

4. Produce CP upto any point D.

Hence, CPD is the required parallel line.

Draw a line MN = 5.8 cm. Locate a point A which is 4.5 cm from M and 5 cm from N. Through A draw a line parallel to line MN.

Answer

Steps:

1. Draw a line MN = 5.8 cm.

2. With M as center and radius equal to 4.5 cm, draw an arc.

3. With N as center and radius equal to 5 cm, draw an arc which cuts previous arc at point A.

4. Take any point P in line MN and join it with the given point A.

5. At point A, construct ∠NPA = ∠PAB.

6. Produce AB upto any point C.

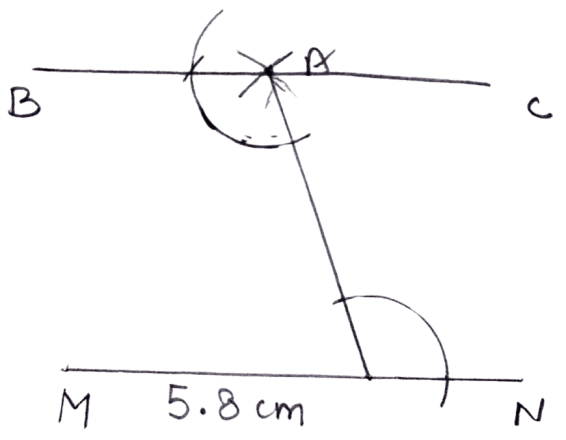
Hence, BAC is the required parallel line.

Draw a straight line AB = 6.5 cm. Draw another line which is parallel to AB at a distance of 2.8 cm from it.

Answer

Steps:

1. Draw a line AB = 6.5cm.

2. At any point P in line AB, draw PQ perpendicular to AB.

3. With P as centre and radius equal to 2.8 cm, draw an arc which cuts PQ at point R.

4. At point R, draw RD perpendicular to PQ.

5. Produce DR upto any point C.

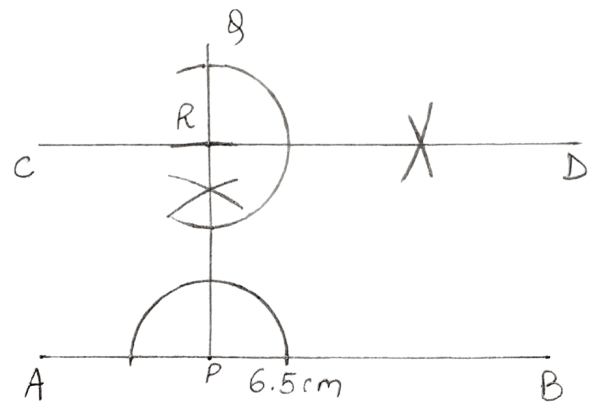
Hence, CD is the required parallel line.

Construct an angle PQR = 60°. Draw a line parallel to PQ at a distance of 3 cm from it and another line parallel to QR at a distance of 3.5 cm from it. Mark the point of intersection of these parallel lines as A.

Answer

Steps:

1. Draw a line segment QR of any suitable length.

2. With Q as centre, draw an arc of any suitable radius which cuts QR at point I.

3. With I as centre and the same radius as taken in step 2, draw one more arc which cuts the previous arc.

4. Join Q with previous intersecting point and produce upto any point P.
   Angle PQR = 60°.

5. At any point C in line PQ, draw CX perpendicular to PQ.

6. With C as centre and radius equal to 3 cm, draw an arc which cuts CX at point D.

7. At point D, draw DE perpendicular to CX.

8. Produce DE upto any point F.
   EF is the parallel line to PQ.

9. At any point B in line QR, draw BY perpendicular to QR.

10. With B as centre and radius equal to 3.5 cm, draw an arc which cuts BY at point G.

11. At point G, draw GJ perpendicular to BY.

12. Produce GJ upto any point H.
    HJ is the parallel line to QR.

13. HJ and EF intersect at point A.

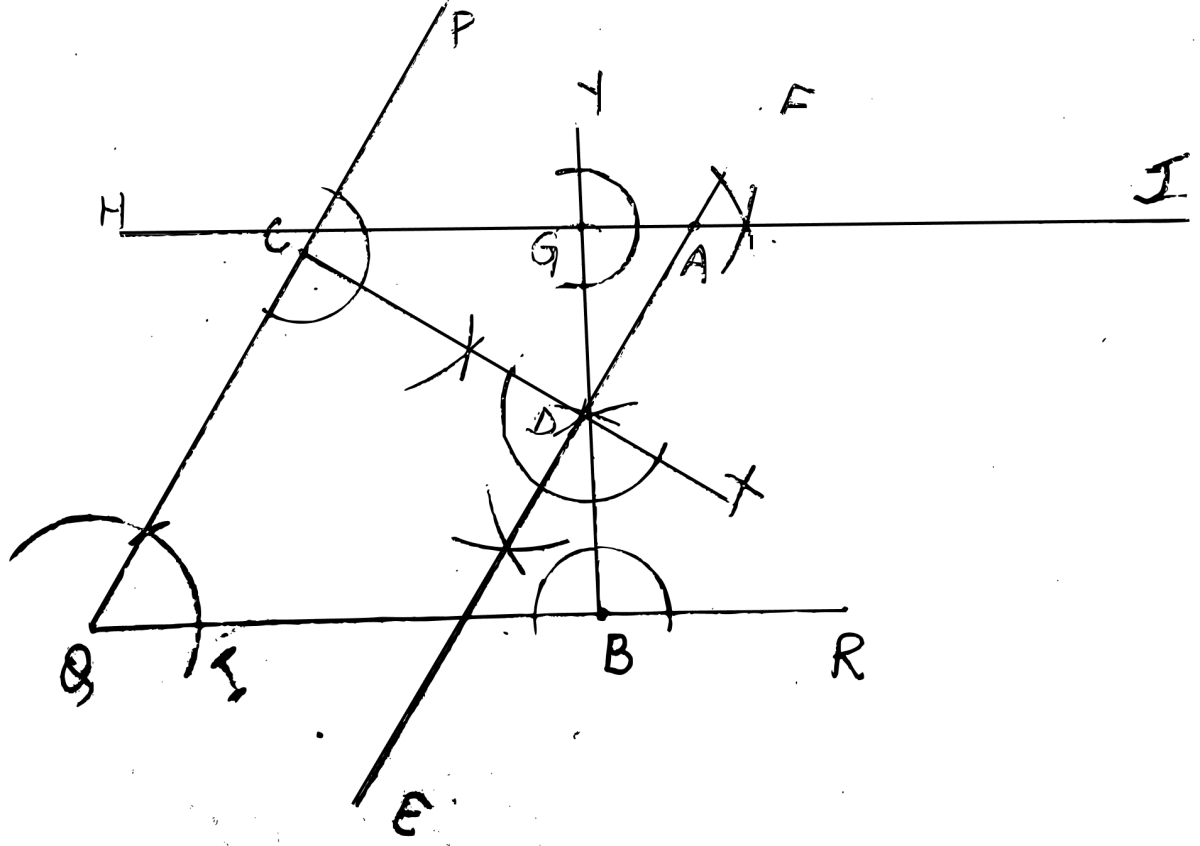
Hence, A is the point of intersection of the parallel lines.

Draw an angle ABC = 60°. Draw the bisector of it. Also draw a line parallel to BC at a distance of 2.5 cm from it.

Let this parallel line meet AB at point P and angle bisectors at point Q. Measure the lengths of BP and PQ. Is BP = PQ ?

Answer

Steps:

1. Draw a line segment BC of any suitable length.

2. With B as centre, draw an arc of any suitable radius which cuts BC at point X.

3. With X as centre and the same radius as taken in step 2, draw one more arc which cuts the previous arc at point D.

4. Join BD and produce upto any point A.
   ∠ ABC = 60°.

5. With D as centre, draw an arc of same radius as taken in step 2.

6. With X as centre, draw an arc of same radius as taken in step 2 and cutting the previous arc at point E.

7. Join B and E.
   BE is angle bisector of angle ABC.

8. At any point F in line BC, draw FW perpendicular to BC.

9. With F as centre and radius equal to 2.5 cm, draw an arc which cuts FW at point R.

10. At point R, draw RY perpendicular to FR.

11. Produce RY upto any point Z.

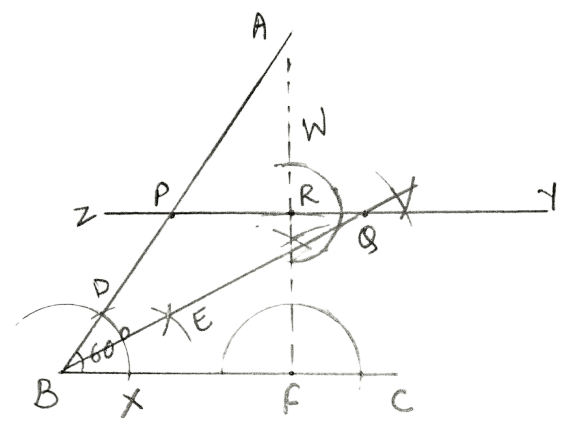
RY is the parallel line to BC at a distance of 2.5 cm from it.

RY meets AB at point P and BE at point Q.

The length of BP = 2.8 cm.

The length of PQ = 2.8 cm.

So, BP = PQ

Hence, the length of BP is equal to that of PQ.

Construct a quadrilateral ABCD; if :

AB = 8 cm, BC = 5.4 cm, AD = 6 cm, ∠A = 60° and ∠B = 75°.

Answer

Steps:

1. Draw AB = 8 cm.

2. At A, construct angle PAB = 60° and at B, construct angle QBA = 75°.

3. From PA cut DA = 6 cm and from QB cut CB = 5.4 cm

4. Join C and D.

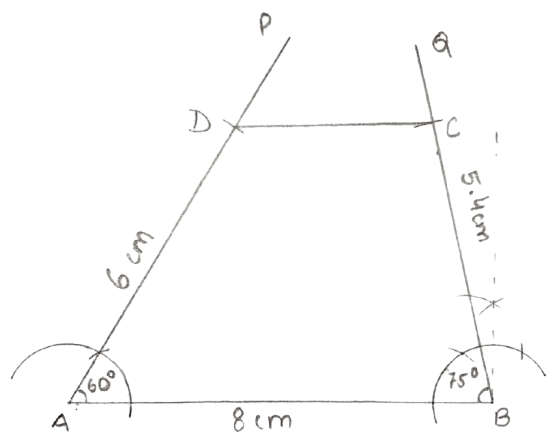
Hence, ABCD is the required quadrilateral.

Construct a quadrilateral ABCD; if :

AB = 6 cm = AC, BC = 4 cm, CD = 5 cm and AD = 4.5 cm.

Answer

Steps:

1. Draw AB = 6cm.

2. Taking B as center, draw an arc of radius 4 cm (= BC) and taking A as center, draw one more arc of radius 6 cm (= diagonal AC). Let the two arcs intersect at point C.

3. Taking C as center, draw an arc of radius 5 cm (= CD) and taking A as center, draw one more arc of radius 4.5 cm (= AD). Let the two arcs intersect at point D.

4. Join AD and CD.

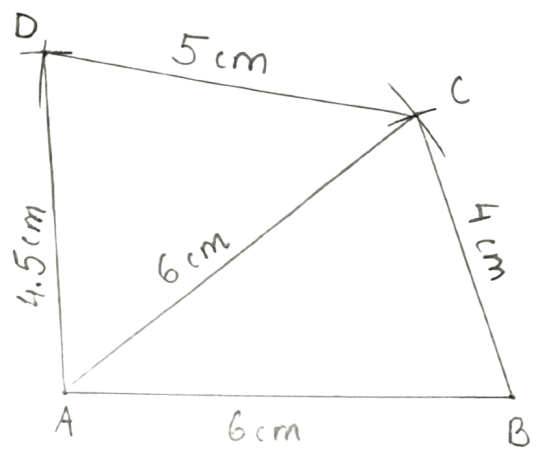
Hence, ABCD is the required quadrilateral.

Construct a quadrilateral ABCD; if :

AB = AD = 5 cm, BD = 7 cm and BC = DC = 5.5 cm.

Answer

Steps:

1. Draw AB = 5 cm.

2. Taking A as center, draw an arc of radius 5 cm (= AD) and taking B as center, draw one more arc of radius 7 cm (= diagonal BD). Let the two arcs intersect at point D.

3. Taking D as center, draw an arc of radius 5.5 cm (= CD) and taking B as center, draw one more arc of radius 5.5 cm(= BC). Let the two arcs intersect at point C.

4. Join DC and BC.

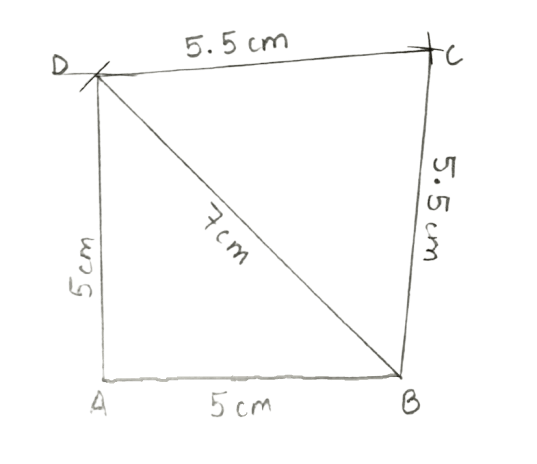
Hence, ABCD is the required quadrilateral.

Construct a parallelogram ABCD, if :

AB = 3.6 cm, BC = 4.5 cm and ∠ABC = 120°.

Answer

Steps:

1. Draw AB = 3.6 cm.

2. At B, construct angle PBA = 120° and from BP cut BC = 4.5 cm.

3. Taking C as center, draw an arc of radius 3.6 cm (= CD) and taking A as center draw one more arc of radius 4.5 cm (= AD). Let the two arcs intersect at point D.

4. Join AD and DC.

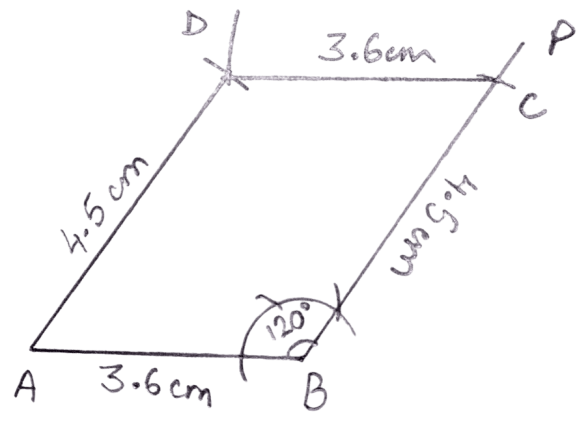
Hence, ABCD is the required parallelogram.

Construct a parallelogram ABCD, if :

BC = 4.5 cm, CD = 5.2 cm and ∠ADC = 60°.

Answer

Steps:

1. Draw CD = 5.2 cm.

2. At D, construct angle PDC = 60° and from PD cut DA = 4.5 cm.

3. Taking A as center, draw an arc of radius 5.2 cm (= AB) and taking C as center draw one more arc of radius 4.5 cm (= CB). Let the two arcs intersect at point B.

4. Join CB and AB.

Hence, ABCD is the required parallelogram.

Construct a parallelogram ABCD, if :

AD = 4 cm, DC = 5 cm and diagonal BD = 7 cm.

Answer

Steps:

1. Draw AD = 4 cm.

2. Taking D as centre, draw an arc of radius 7 cm (= diagonal BD) and taking A as centre draw one more arc of radius 5 cm (= AB). Let the two arcs intersect at point B. Join A and B.

3. Taking B as centre, draw an arc of radius 4 cm (= BC) and taking D as centre draw one more arc of radius 5 cm (= DC). Let the two arcs intersect at point C.

4. Join DC and BC.

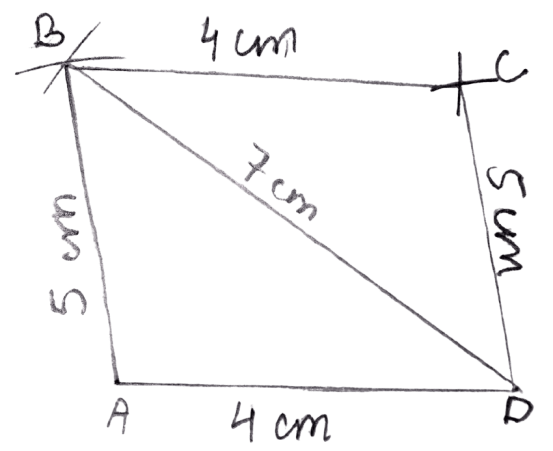
Hence, ABCD is the required parallelogram.

Construct a parallelogram ABCD, if :

diagonal AC = 6.4 cm, diagonal BD = 5.6 cm and angle between the diagonals is 75°.

Answer

Steps:

1. Draw AC = 6.4 cm.

2. Locate the mid-point O of AC by drawing its perpendicular bisector.

3. Through O, construct a line EOF so that angle EOC = 75°.

4. From OE, cut OB = $\dfrac{BD}{2}$ = $\dfrac{5.6}{2}$ = 2.8 cm and also OD = $\dfrac{BD}{2}$ = $\dfrac{5.6}{2}$ = 2.8 cm

5. Join AB, BC, CD and DA.

Hence, ABCD is the required parallelogram.

Construct a rectangle ABCD; if:

AB = 4.5 cm and BC = 5.5 cm.

Answer

Steps:

1. Draw AB = 4.5 cm.

2. At B, construct angle PBA = 90°. From BP cut BC = 5.5cm.

3. Taking C as centre, draw an arc of radius 4.5 cm (= AB) and taking A as centre, draw one more arc of radius 5.5 cm (= BC). Let these two arcs intersect at point D.

4. Join AD and CD.

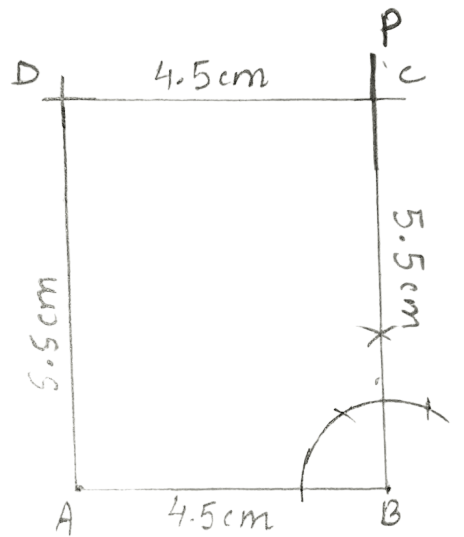
Hence, ABCD is the required rectangle.

Construct a rectangle ABCD; if:

AB = 5.0 cm and diagonal AC = 6.7 cm.

Answer

Steps:

1. Draw AB = 5 cm.

2. At B, construct angle PBA = 90°.

3. Taking A as centre, draw an arc of radius 6.7 cm (= AC) which cuts BP at point C.

4. Taking C as centre, draw an arc of radius 5 cm (= AB) and taking A as centre draw another arc of radius equal to BC. Let these two arcs intersect at point D.

5. Join AD and CD.

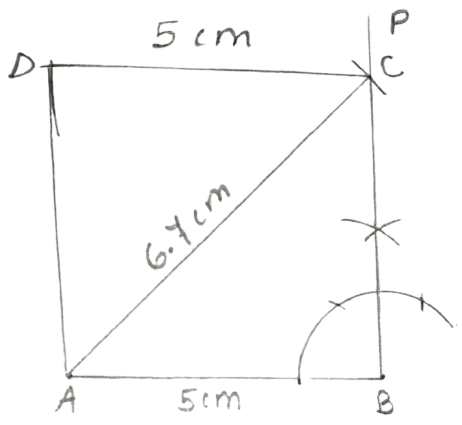
Hence, ABCD is the required rectangle.

Construct a rectangle ABCD; if:

each diagonal is 6 cm and the angle between them is 45°.

Answer

Steps:

1. Draw AC = 6 cm.

2. Draw the perpendicular bisector of AC to locate the mid-point of AC. Let the perpendicular bisector intersect AC at point O. Therefore, O is the mid-point of AC.

3. Through O, construct a line POQ so that angle POC = 45°.

4. From OP cut OD equal to OC (i.e. 3 cm) and from OQ cut OB equal to OA (i.e. 3 cm).

5. Join AB, BC, CD and DA.

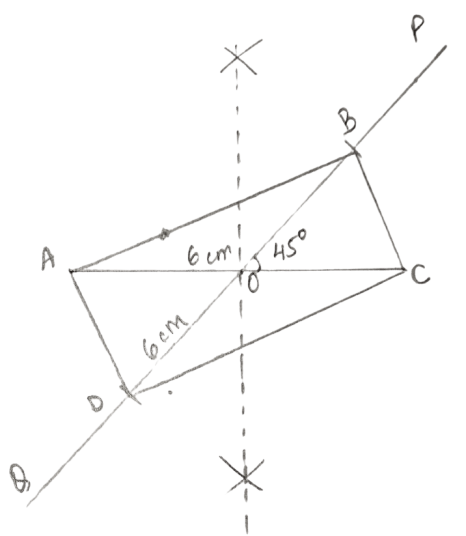
Hence, ABCD is the required rectangle.

Construct a rhombus ABCD, if:

AB = 4 cm and ∠B = 120°.

Answer

Steps:

1. Draw AB = 4 cm.

2. At B, construct angle PBA = 120°.

3. From PB, cut BC = 4 cm.

4. Taking C as centre, draw an arc of radius 4 cm (= AB) and taking A as centre draw one more arc of radius 4 cm (= AB). Let the two arcs intersect at point D.

5. Join CD and AD.

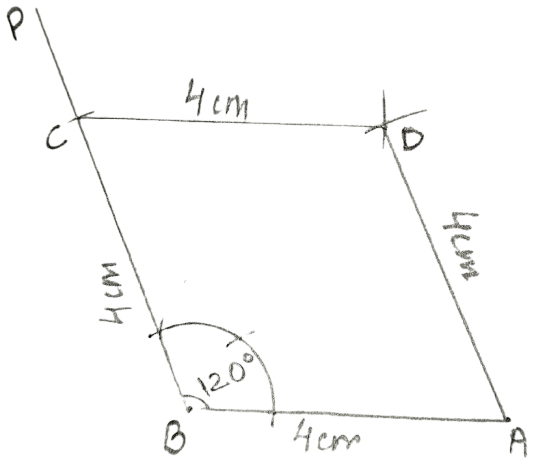
Hence, ABCD is the required rhombus.

Construct a rhombus ABCD, if:

CD = 5 cm and diagonal BD = 8.5 cm.

Answer

Steps:

1. Draw CD = 5 cm.

2. Taking D as centre, draw an arc of radius 8.5 cm (= BD) and taking C as centre, draw one more arc of radius 5cm (= CB). Let the two arcs intersect at point B.

3. Taking D as centre, draw an arc of radius 5 cm (= AD) and taking B as centre, draw one more arc of radius 5cm (= AB). Let the two arcs intersect at point A.

4. Join DA, AB and CB.

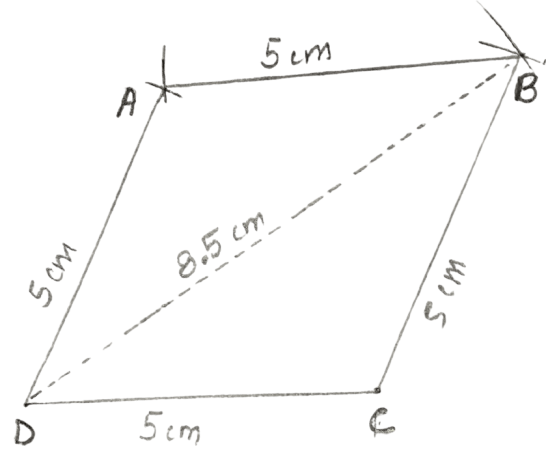
Hence, ABCD is the required rhombus.

Construct a rhombus ABCD, if:

BC = 4.8 cm and diagonal AC = 7 cm.

Answer

Steps:

1. Draw BC = 4.8 cm.

2. Taking C as centre, draw an arc of radius 7 cm (= AC) and taking B as centre, draw one more arc of radius 4.8 cm (= AB). Let the two arcs intersect at point A.

3. Taking C as centre, draw an arc of radius 4.8 cm (= DC) and taking A as centre, draw one more arc of radius 4.8 cm (= AD). Let the two arcs intersect at point D.

4. Join AB, AC and DA.

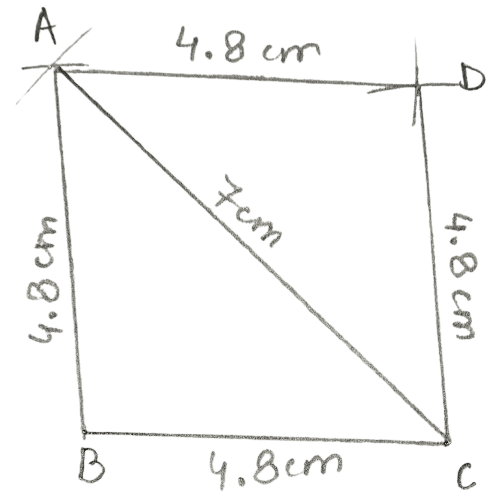
Hence, ABCD is the required rhombus.

Construct a rhombus ABCD, if:

diagonal AC = 6.6 cm and diagonal BD = 5.8 cm.

Answer

Steps:

1. Draw AC = 6.6 cm.

2. Draw the perpendicular bisector of AC. Let PQ be the perpendicular bisector of AC which bisects AC at point O.

3. From OP, cut OD = $\dfrac{BD}{2}$ = $\dfrac{5.8}{2}$ = 2.9 cm and from OQ, cut OB = $\dfrac{BD}{2}$ = 2.9 cm.

4. Join AB, BC, CD and DA.

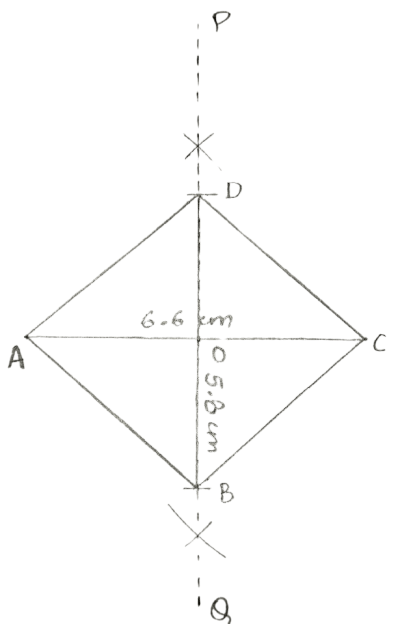
Hence, ABCD is the required rhombus.

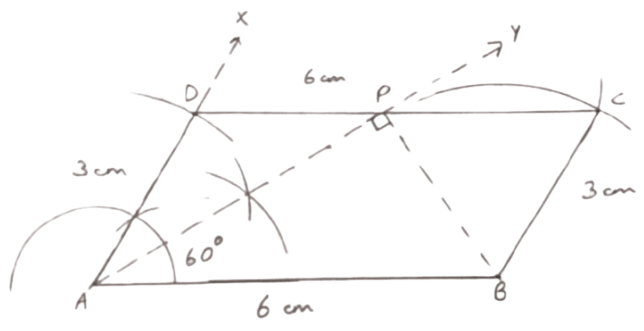
Using ruler and compasses only, construct a parallelogram ABCD, in which: AB = 6 cm, AD = 3 cm and ∠DAB = 60°.

In the same figure draw the bisector of angle DAB and let it meet DC at point P. Measure angle APB.

Answer

Steps:

1. Draw a line segment AB = 6 cm.

2. At A, construct angle XAB = 60° and from XA cut AD = 3 cm.

3. Taking B as center, draw an arc of radius 3 cm (= AD) and taking D as center draw one more arc of radius 6 cm (= AB). Let the two arcs intersect at point C.

4. Join BC and DC. Hence, ABCD is the required parallelogram.

5. Draw AY, the angle bisector of A.

6. Mark point P as the intersection of line AY and DC.

7. Join PB. Measure ∠APB.

Hence, ∠APB = 90°.

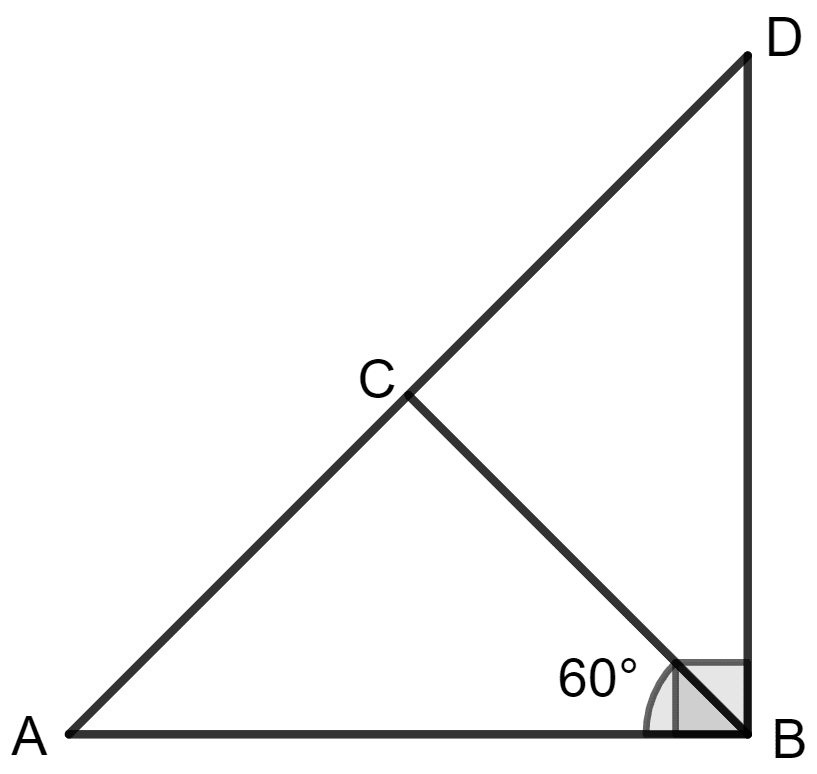
Let angle ABC = 60° and angle ABD = 90°, then ∠CBD is equal to:

1. 150°

2. 30°

3. 150° or 30°

4. none of these

Answer

From figure (i),

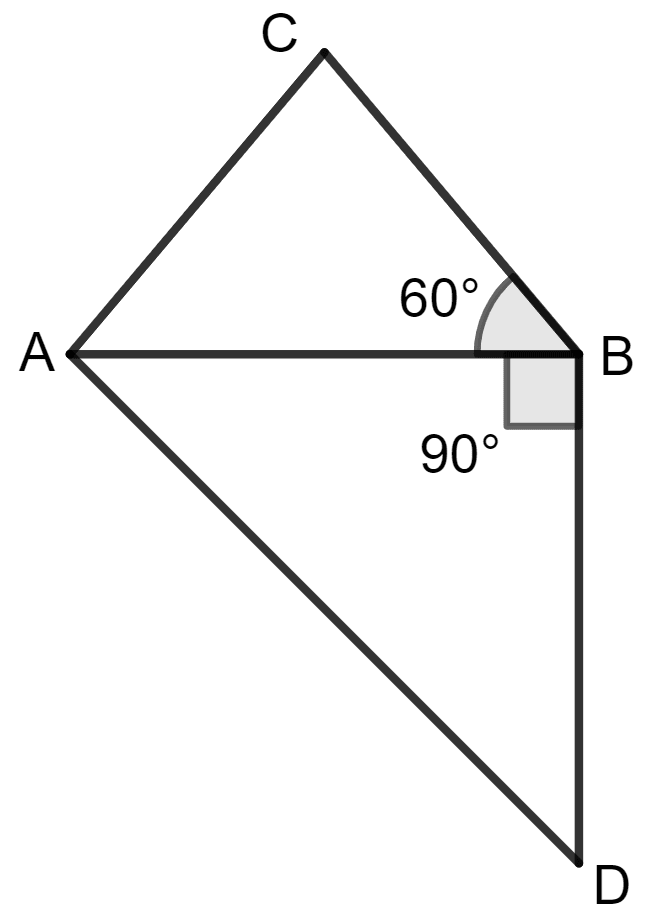
∠ CBD = ∠ ABD + ∠ ABC

= 90° + 60°

= 150°

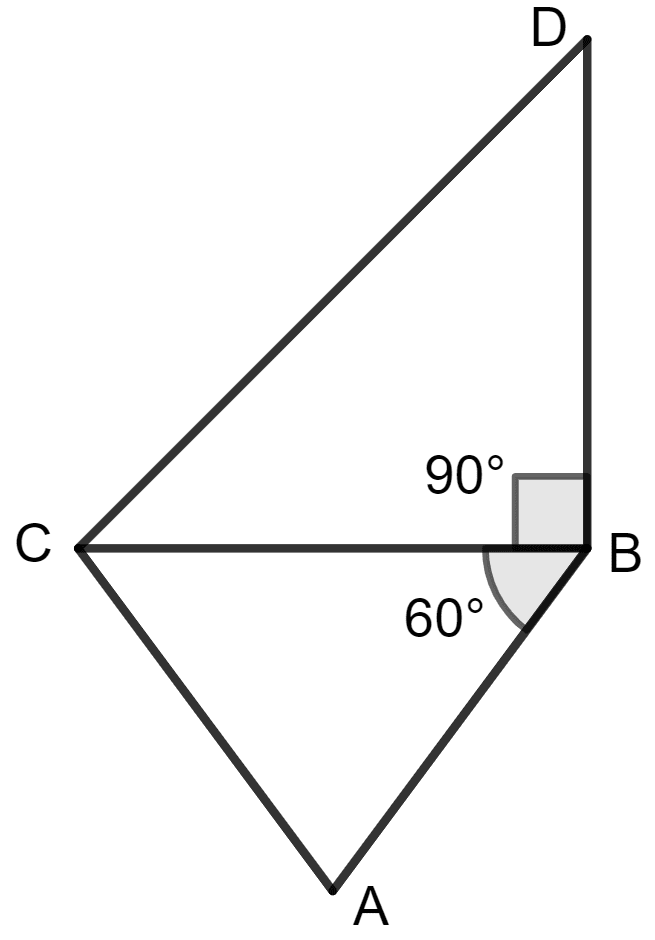
From figure (ii),

∠ CBD = ∠ ABD - ∠ ABC

= 90° - 60°

= 30°

From figure (iii),

∠ CBD = 90°

Hence, option 4 is the correct option.

The shortest distance between the point P and the line segment AB is:

1. PA

2. PB

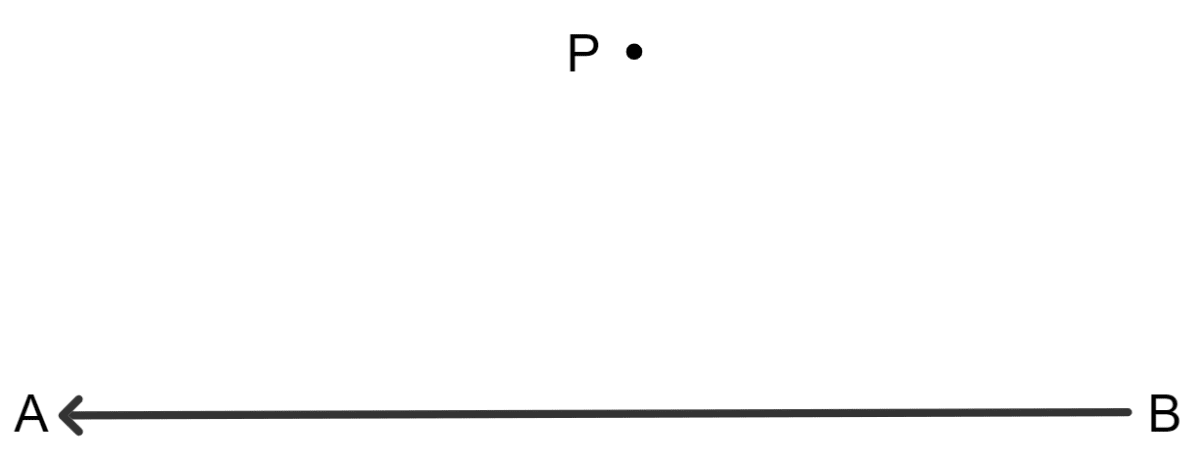
3. line joining point P with the mid-point of AB.

4. length of perpendicular from point P to line AB.

Answer

The shortest distance from the given line is the length of the perpendicular from the point to the line.

Hence, option 4 is the correct option.

Two lines AB and CD are not parallel to each other, when they are cut by a transversal with:

1. vertically opposite angles are equal.

2. corresponding angles are equal

3. alternate angles are equal

4. co-interior angles are supplementary.

Answer

Two lines AB and CD are not parallel to each other when they are cut by a transversal if the vertically opposite angles are equal.

Hence, option 1 is the correct option.

A parallelogram will not be a rhombus if :

1. sum of its opposite angles is 180°

2. its adjacent sides are equal.

3. its diagonals are perpendicular to each other.

4. each diagonal bisects the angles of the vertices.

Answer

A parallelogram will not be a rhombus if the sum of its opposite angles is 180°.

Hence, option 1 is the correct option.

A rectangle will not be a square, if :

1. adjacent sides are equal

2. angle between the diagonals is 90°

3. diagonals bisect each other and the angle between them is not 90°

4. all its sides are equal.

Answer

A rectangle will not be a square if its diagonals bisect each other and the angle between them is not 90°.

Hence, option 3 is the correct option.

Given below are the angles x, y and z.

Without measuring these angles construct :

(i) ∠ABC = x + y + z

(ii) ∠ABC = 2x + y + z

(iii) ∠ABC = x + 2y + z

Answer

(i) Steps:

1. Draw line segment BC of any suitable length.

2. With B as centre, draw an arc of any suitable radius. With the same radius, draw arcs with the vertices of given angles as centres. Let these arcs cut arms of the angle x at the points Q and P, arms of the angle y at points S and R and arms of the angles z at points T and U.

3. From the arc, with centre B, cut MN = PQ = x, NO = SR = y and OX = TU = z.

4. Joint BX and produce upto point A.

Hence, ∠ ABC = x + y + z.

(ii) Steps:

1. Draw line segment BC of any suitable length.

2. With B as centre, draw an arc of any suitable radius. With the same radius, draw arcs with the vertices of given angles as centres. Let these arcs cut arms of the angle x at the points P and Q, arms of the angles y at points R and S and arms of the angles z by at the points T and U.

3. From the arc, with centre B, cut MN = PQ = x, NO = PQ = x , OX = RS = y and XY = TU = z.

4. Joint BY and produce upto point A.

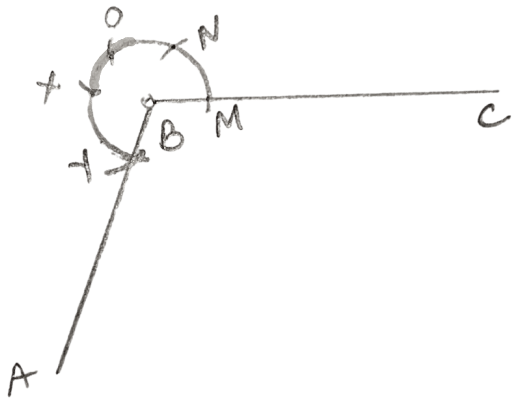
Hence, ∠ABC = 2x + y + z.

(iii) Steps:

1. Draw line segment BC of any suitable length.

2. With B as centre, draw an arc of any suitable radius. With the same radius, draw arcs with the vertices of given angles as centres. Let these arcs cut arms of the angle x at the points P and Q, arms of the angle y at points R and S, and arms of the angle z at points T and U.

3. From the arc, with centre B, cut MN = PQ = x, NO = SR = y, OX = SR = y and XY = TU = z.

4. Joint BY and produce upto point A.

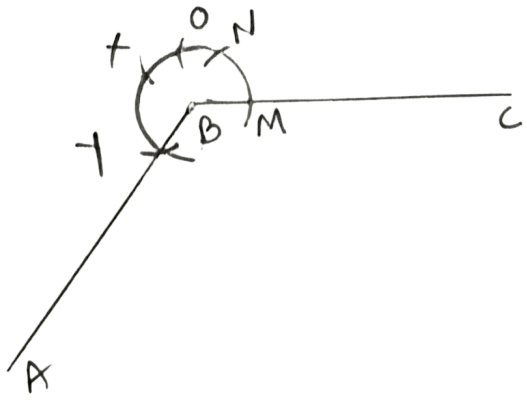
Hence, ∠ABC = x + 2y + z.

Draw a line segment AB = 6.2 cm. Mark a point P in AB such that BP = 4 cm. Through point P draw a perpendicular to AB.

Answer

Steps:

1. Draw a line AB = 6.2 cm.

2. Make a point P on AB such that BP = 4 cm.

3. With P as center, draw an arc with a suitable radius which cuts AB at points C and D.

4. Taking C and D as centers, draw arcs of equal radii which cut each other at point H.
   (The radius must be more than half the distance between C and D.)

5. Join P and H.

So, ∠HPA = ∠HPB = 90°.

Hence, HP is the required perpendicular.

Construct an angle ABC = 90°. Locate a point P which is 2.5 cm from AB and 3.2 cm from BC.

Answer

Steps:

1. Draw a line segment BC of any suitable length.

2. Taking B as centre, draw an arc of any suitable radius, which cuts BC at point E.

3. With E as centre and the same radius, as taken in step 2, draw an arc which cuts previous arc at point F.

4. With F as centre and the same radius, draw one more arc which cuts the first arc at point G.

5. With F and G as centres and radii equal to more than half the distance between F and G, draw arcs which cut each other at point H.

6. Join BH and produce upto any point A.
   ∠ABC so obtained is equal to 90° i.e., ∠ABC = 90°.

7. Taking any point Y on line BC and radii 3.2 cm, draw an arc.

8. Taking any point X on line AB and radii 2.5 cm, draw an arc which cut the arc drawn in step 7 at P.

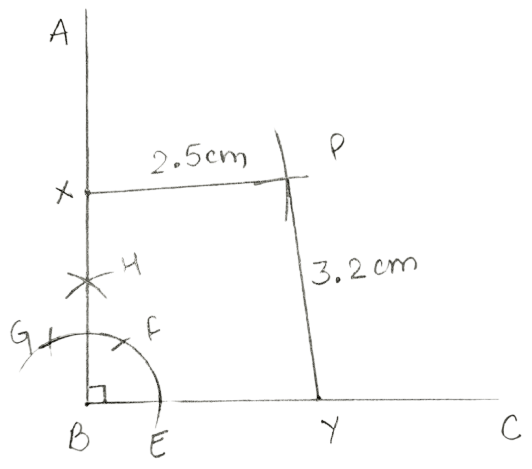
Hence, length of PX = 2.5 cm and PY = 3.2 cm.

Construct a quadrilateral ABCD; if :

AB = 4.3 cm, BC = 5.4 cm, CD = 5 cm, DA = 4.8 cm and angle ABC = 75°.

Answer

Steps:

1. Draw AB = 4.3 cm.

2. At B, construct angle PBA = 75°.

3. From PB cut BC = 5.4 cm.

4. With A as center and radius equal to 4.8 cm, draw an arc.

5. With C as center and radius equal to 5 cm, draw an arc which intersects the arc drawn in step 4 at D.

6. Join DA and DC.

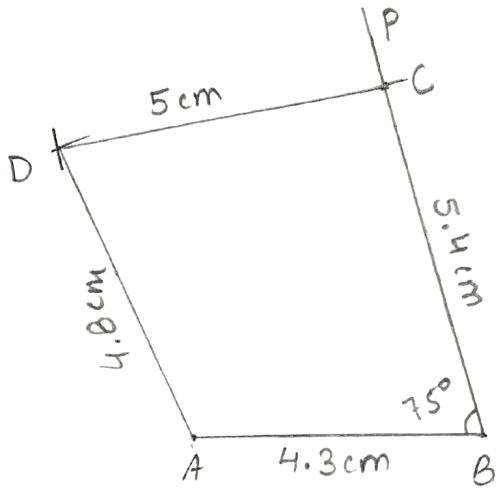
Hence, ABCD is the required quadrilateral.

Construct a quadrilateral ABCD; if :

AB = 6 cm, CD = 4.5 cm, BC = AD = 5 cm and ∠BCD = 60°.

Answer

Steps:

1. Draw BC = 5 cm.

2. With C as centre, draw an arc of any suitable radius which cuts BC at point R.

3. With R as centre and the same radius as taken in step 2, draw one more arc which cuts the previous arc.

4. Join I with C and produce upto any point P.
   ∠PCB = 60°.

5. From PC cut CD = 4.5 cm.

6. With D as center and radius equal to 5 cm, draw an arc.

7. With B as center and radius equal to 6 cm, draw an arc which intersects the arc drawn in step 4 at D.

8. Join BA and AD.

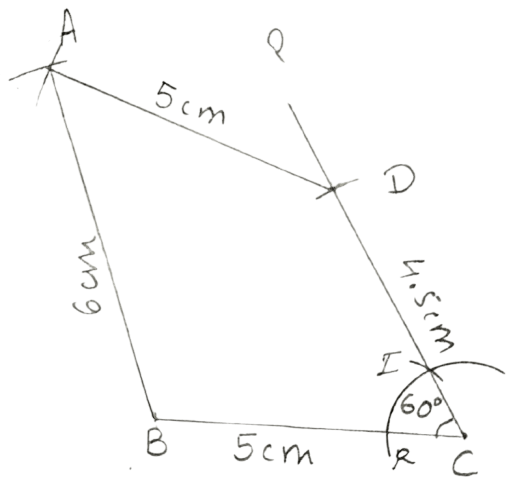
Hence, ABCD is the required quadrilateral.

Construct a quadrilateral ABCD; if :

AB = 5 cm, BC = 6.5 cm, CD = 4.8 cm, ∠B = 75° and ∠C = 120°.

Answer

Steps:

1. Draw BC = 6.5 cm.

2. At B, construct angle PBC = 75° and at C, construct angle QCB = 120°.

3. From PB cut AB = 5 cm and from QC cut DC = 4.8 cm

4. Join A and D.

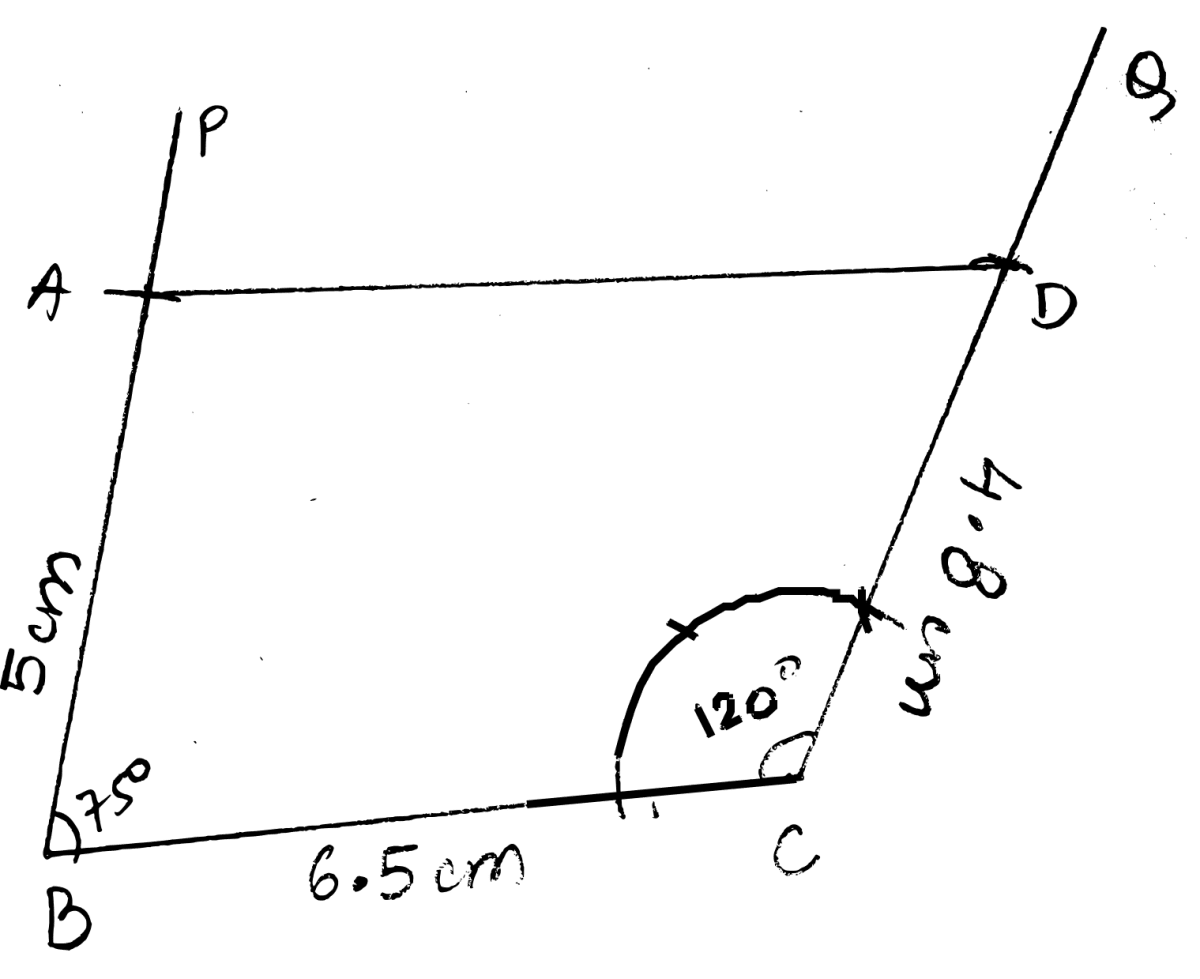
Hence, ABCD is the required quadrilateral.

Construct a parallelogram ABCD, if :

AB = 5.8 cm, AD = 4.6 cm and diagonal AC = 7.5 cm.

Answer

Steps:

1. Draw AB = 5.8 cm.

2. Taking A as centre, draw an arc of radius 7.5 cm (= diagonal AC) and taking B as centre draw one more arc of radius 4.6 cm (= BC). Let the two arcs intersect at point C. Join AC and BC.

3. Taking C as centre, draw an arc of radius 5.8 cm (= DC ) and taking A as centre draw one more arc of radius 4.6 cm (= AD). Let the two arcs intersect at point D.

4. Join AD.

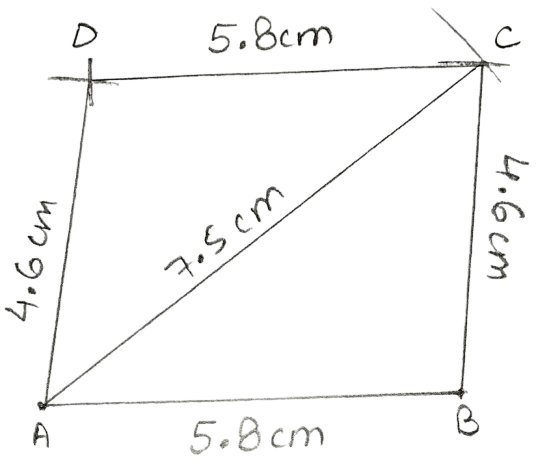
Hence, ABCD is the required parallelogram.

Construct a parallelogram ABCD, if :

lengths of diagonals AC and BD are 6.3 cm and 7.0 cm respectively, and the angle between them is 45°.

Answer

Steps:

1. Draw AC = 6.3 cm.

2. Locate the mid-point O of AC by drawing its perpendicular bisector.

3. Through O, construct a line EOF so that angle EOC = 45°.

4. From EF, cut OD = $\dfrac{BD}{2}$ = $\dfrac{7}{2}$ = 3.5 cm and also OC = $\dfrac{BD}{2}$ = $\dfrac{7}{2}$ = 3.5 cm

5. Join AB, BC, CD and DA.

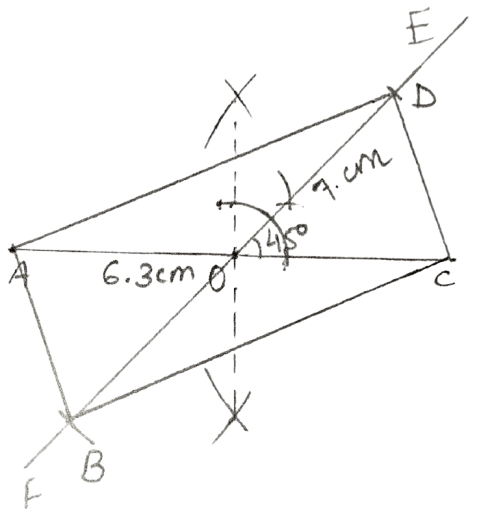
Hence, ABCD is the required parallelogram.

Construct a parallelogram ABCD, if :

lengths of diagonals AC and BD are 5.4 cm and 6.7 cm respectively, and the angle between them is 60°.

Answer

Steps:

1. Draw BD = 6.7 cm.

2. Locate the mid-point O of BD by drawing its perpendicular bisector.

3. Through O, construct a line EOF so that angle EOD = 60°.

4. From EF, cut OC = $\dfrac{AC}{2}$ = $\dfrac{5.4}{2}$ = 2.7 cm and also OA = $\dfrac{AC}{2}$ = $\dfrac{5.4}{2}$ = 2.7 cm

5. Join AB, BC, CD and DA.

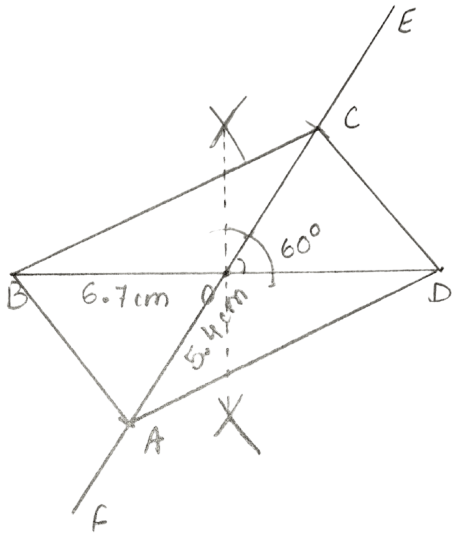
Hence, ABCD is the required parallelogram.

Construct a rectangle ABCD; if :

BC = 6.1 cm and CD = 6.8 cm.

Answer

Steps:

1. Draw BC = 6.1 cm.

2. At C, construct angle ECB = 90°. From EC cut DC = 6.8 cm.

3. Taking D as centre, draw an arc of radius 6.1 cm (= BC) and taking B as centre, draw one more arc of radius 6.8 cm (= CD). Let these two arcs intersect at point A.

4. Join AB and AD.

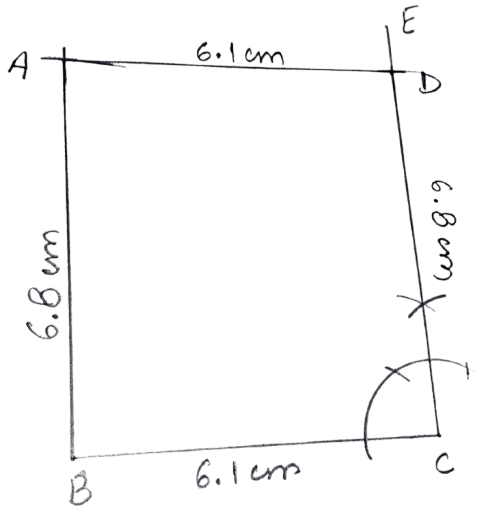
Hence, ABCD is the required rectangle.

Construct a rectangle ABCD; if :

AD = 4.8 cm and diagonal AC = 6.4 cm.

Answer

Steps:

1. Draw AD = 4.8 cm.

2. At D, construct angle EDA = 90°.

3. Taking A as centre, draw an arc of radius 6.4 cm (= AC) which cuts ED at point C.

4. Taking C as centre, draw an arc of radius 4.8 cm (= AD) and taking A as centre draw another arc of radius equal to DC. Let these two arcs intersect at point B.

5. Join AB and CB.

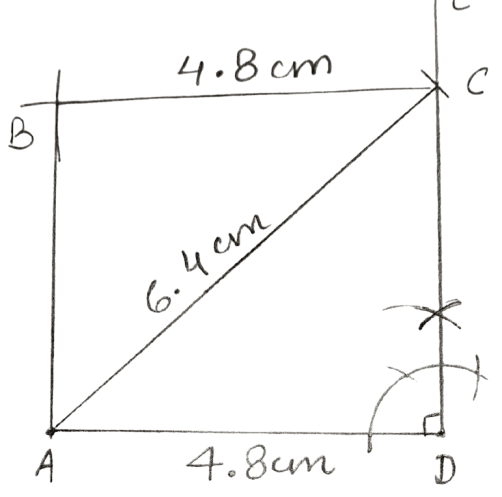
Hence, ABCD is the required rectangle.

Construct a rectangle ABCD; if :

each diagonal is 5.5 cm and the angle between them is 60°.

Answer

Steps:

1. Draw AC = 5.5 cm.

2. Draw the perpendicular bisector of AC to locate the mid-point of AC. Let the perpendicular bisector intersect AC at point O. Therefore, O is the mid-point of AC.

3. Through O, construct a line EOF so that angle EOC = 60°.

4. From OE cut OB equal to OC (i.e., 2.7 cm) and from OF cut OD equal to OA (i.e., 2.7 cm).

5. Join AB, BC, CD and DA.

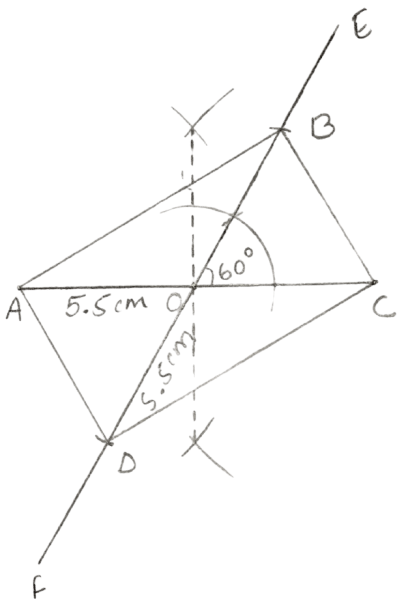
Hence, ABCD is the required rectangle.

Construct a rhombus ABCD, if :

BC = 4.7 cm and ∠B = 75°.

Answer

Steps:

1. Draw BC = 4.7 cm.

2. At B, construct angle EBC = 75°.

3. From EB, cut BA = 4.7 cm.

4. Taking A as centre, draw an arc of radius 4.7 cm (= BC) and taking C as centre draw one more arc of radius 4.7 cm (= BC). Let the two arcs intersect at point D.

5. Join CD and AD.

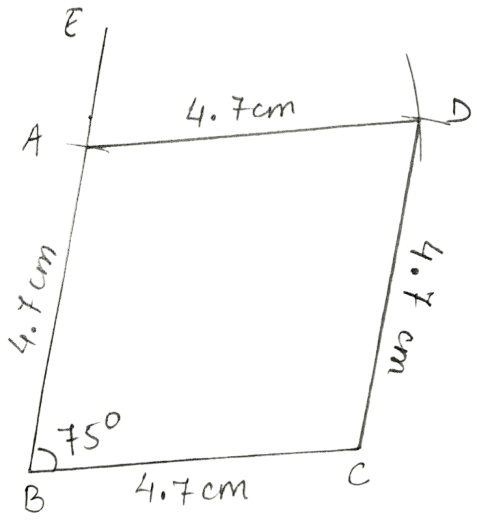
Hence, ABCD is the required rhombus.

Construct a rhombus ABCD, if :

diagonal AC = 4.9 cm and diagonal BD = 6 cm.

Answer

Steps:

1. Draw AC = 4.9 cm.

2. Draw the perpendicular bisector of AC. Let EF be the perpendicular bisector of AC which bisects AC at point O.

3. From OE, cut OB = $\dfrac{BD}{2}$ = $\dfrac{6}{2}$ = 3 cm and from OF, cut OD = $\dfrac{BD}{2}$ = 3 cm.

4. Join AB, BC, CD and DA.

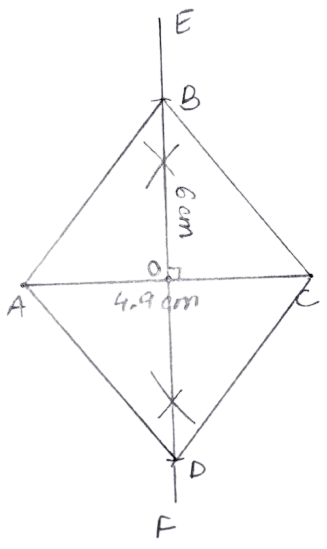
Hence, ABCD is the required rhombus.

Construct a rhombus ABCD, if :

diagonal AC = 8 cm and diagonal BD = 6 cm.

Answer

Steps:

1. Draw AC = 8 cm.

2. Draw the perpendicular bisector of AC. Let EF be the perpendicular bisector of AC which bisects AC at point O.

3. From OE, cut OB = $\dfrac{BD}{2}$ = $\dfrac{6}{2}$ = 3 cm and from OF, cut OD = $\dfrac{BD}{2}$ = 3 cm.

4. Join AB, BC, CD and DA.

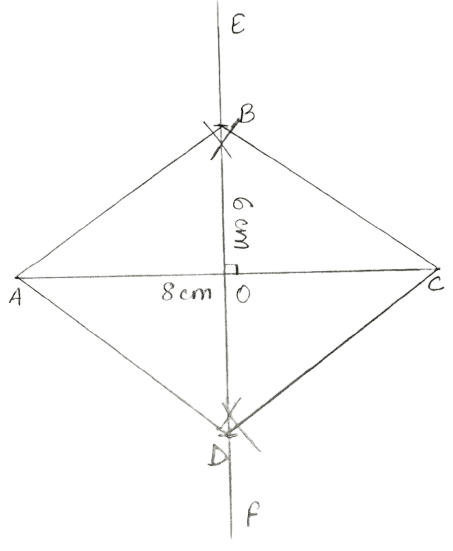
Hence, ABCD is the required rhombus.

Construct a quadrilateral ABCD in which ∠A = 120°, ∠B = 60°, AB = 4 cm, BC = 4.5 cm and CD = 5 cm.

Answer

Steps:

1. Draw AB = 4 cm.

2. At A, construct ∠EAB = 120° and at B, construct ∠FBA = 60°.

3. From FB, cut CB = 4.5 cm.

4. With C as center, and radius = 5 cm cut an arc on line EA at point D.

5. Join C and D.

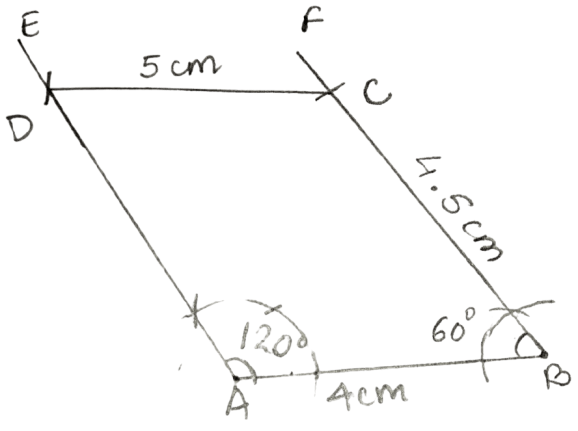
Hence, ABCD is the required quadrilateral.

Construct a quadrilateral ABCD, such that AB = BC = CD = 6 cm, ∠B = 90° and ∠C = 120°.

Answer

Steps:

1. Draw BC = 6 cm.

2. At B, construct ∠EBC = 90° and at C, construct ∠FCB = 120°.

3. From EB cut AB = 6 cm and from FC cut DC = 6 cm.

4. Join A and D.

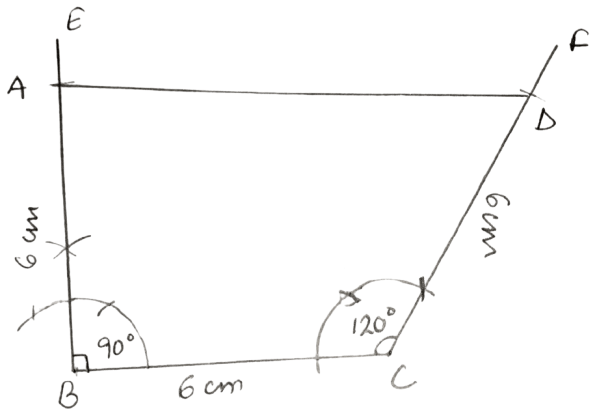
Hence, ABCD is the required quadrilateral.

Draw a parallelogram ABCD, with AB = 7 cm, AD = 6 cm and ∠DAB = 45°.

Draw the perpendicular bisector of side AD and let it meet AD at point P. Also, draw the diagonals AC and BD, and let them intersect at point O. Join O and P. Measure OP.

Answer

Steps:

1. Draw AB = 7 cm.

2. At A, construct angle GAB = 45° and from GA cut DA = 6 cm.

3. Taking B as center, draw an arc of radius 6 cm (= AD) and taking D as center draw one more arc of radius 7 cm (= AB). Let the two arcs intersect at point C.

4. Join DC and BC.
   ABCD is the required parallelogram.

5. With A as center, and radius equal to more than half of AD, draw arcs on both sides of AD.

6. With D as center and with the same radius as taken in step 5, draw arcs on both the sides of AD.

7. Let the arcs intersect each other at X and Y.

8. Join X and Y.

9. The line XY intersects the line AD at P.

10. Join BD and AC and they intersect each other at O.

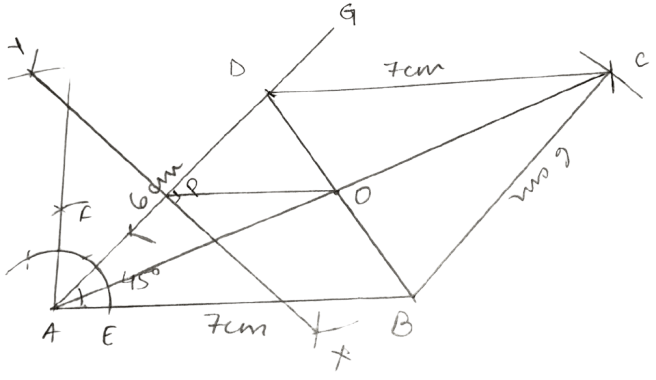
Hence, the length of OP = 3.5 cm.