Rectilinear Figures

If two angles of a quadrilateral are 40° and 110° and the other two are in the ratio 3 : 4, find these angles.

Answer

Sum of angles of quadrilateral = 360°.

Let other two angles be 3x and 4x.

∴ 3x + 4x + 40° + 110° = 360°

⇒ 7x + 150° = 360°

⇒ 7x = 360° - 150°

⇒ 7x = 210°

⇒ x = $\dfrac{210°}{7}$

⇒ x = 30°

⇒ 3x = 3(30°) = 90° and 4x = 4(30°) = 120°.

Hence, other two angles are 90° and 120°.

If the angles of a quadrilateral, taken in order, are in the ratio 1 : 2 : 3 : 4, prove that it is a trapezium.

Answer

Let a trapezium be ABCD.

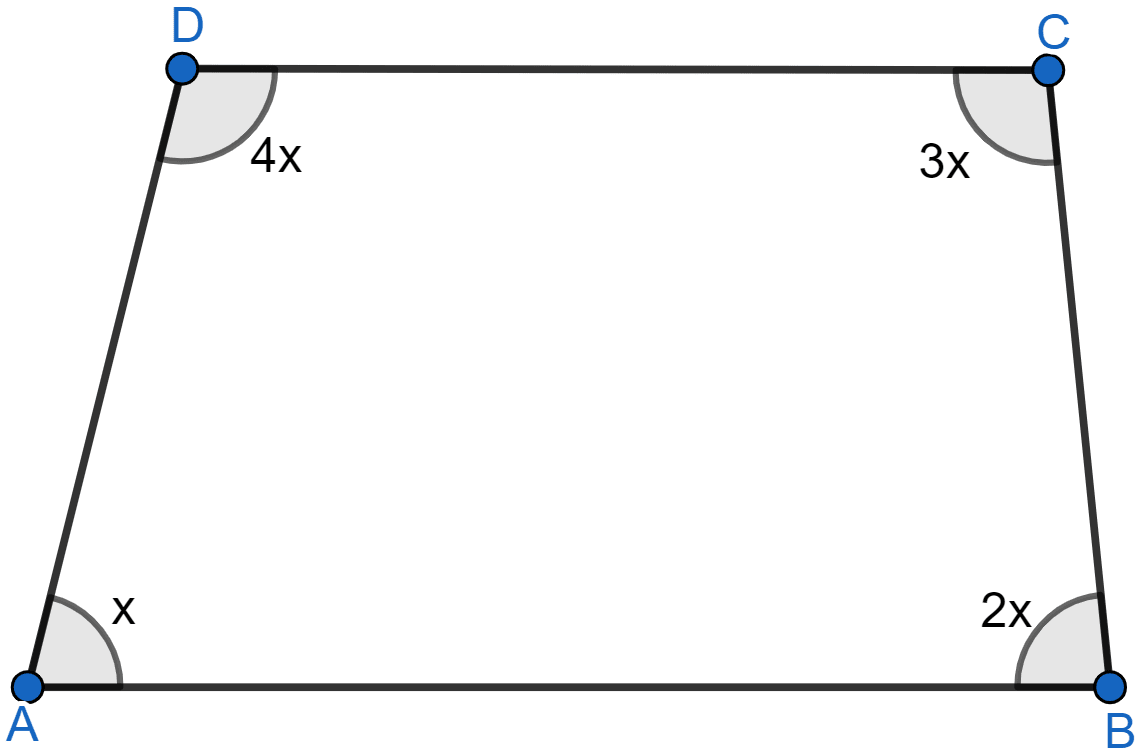
Let angles be x, 2x, 3x and 4x taken in order.

Sum of angles of quadrilateral = 360°.

∴ x + 2x + 3x + 4x = 360°

⇒ 10x = 360°

⇒ x = $\dfrac{360°}{10}$

⇒ x = 36°.

⇒ ∠A = x = 36°,

⇒ ∠B = 2x = 2(36°) = 72°

⇒ ∠C = 3x = 3(36°) = 108°

⇒ ∠D = 2x = 4(36°) = 144°.

From figure,

∠A and ∠D are co-interior angles and their sum = 180° (36° + 144°).

Sum of co-interior angles = 180°, which means AB and CD are parallel.

Also,

Opposite angles sum i.e.

∠A + ∠C = 36° + 108° = 144°,

∠B + ∠D = 72° + 144° = 216°.

Since, the sum of opposite angles ≠ 180° (Property of trapezium).

Hence, proved that ABCD is a trapezium.

If an angle of a parallelogram is two-thirds of its adjacent angle, find the angles of the parallelogram.

Answer

Let a parallelogram be ABCD.

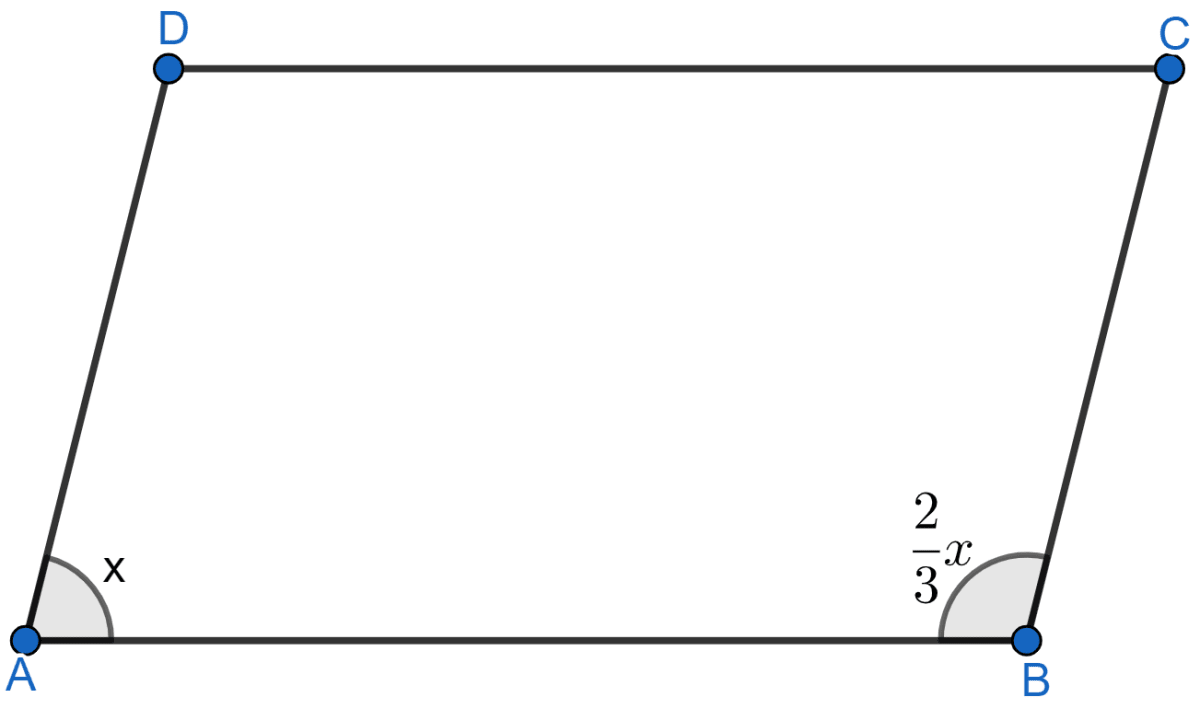
Let ∠A = x and so adjacent angle (∠B) = $\dfrac{2}{3}x$

As AD || BC, sum of co-int ∠s = 180°,

$\therefore x + \dfrac{2}{3}x = 180° \\[1em] \Rightarrow \dfrac{3x + 2x}{3} = 180° \\[1em] \Rightarrow \dfrac{5x}{3} = 180° \\[1em] \Rightarrow x = \dfrac{180° \times 3}{5} \\[1em] \Rightarrow x = 108° \\[1em] \Rightarrow \dfrac{2x}{3} = \dfrac{2 \times 108°}{3} = 72°.$

Opposite angles of a parallelogram are equal.

∴ ∠C = ∠A = 108° and ∠D = ∠B = 72°

Hence, angles of parallelogram are 108°, 72°, 108° and 72°.

In the figure (1) given below, ABCD is a parallelogram in which ∠DAB = 70°, ∠DBC = 80°. Calculate angles CDB and ADB.

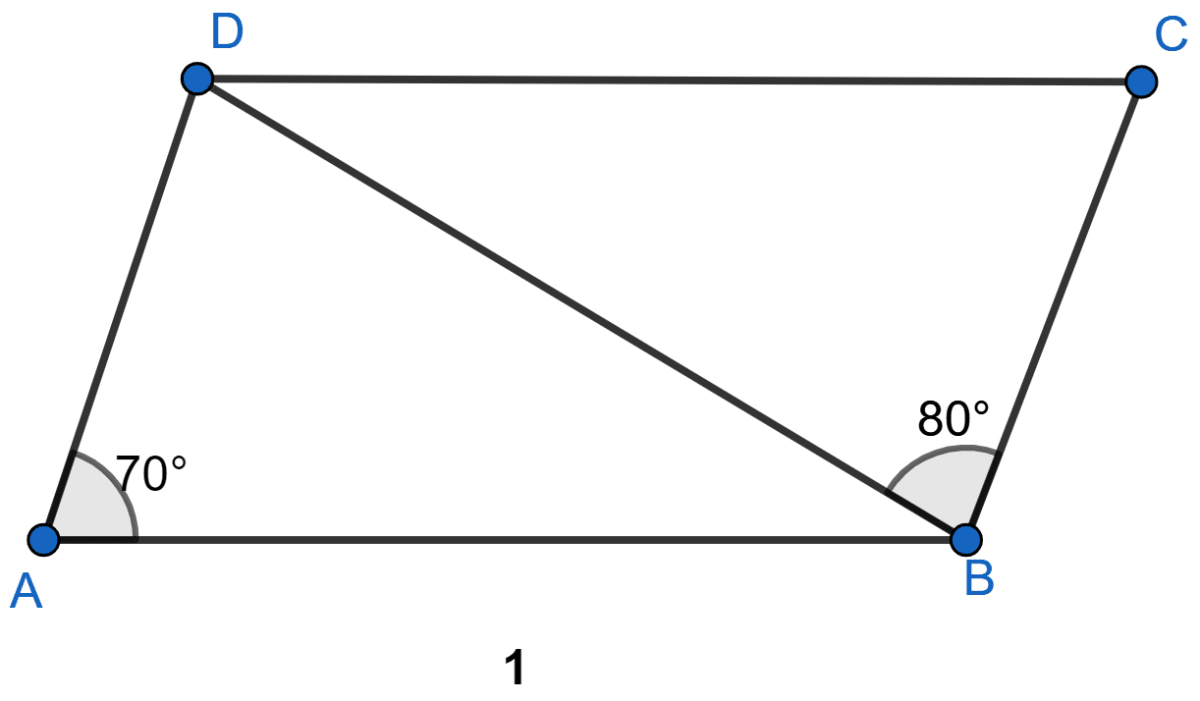
Answer

As AD || BC, sum of co-int ∠s = 180°.

∠A + ∠B = 180°

∠B = 180° - ∠A = 180° - 70° = 110°.

From figure,

⇒ ∠B = ∠DBA + ∠DBC

⇒ 110° = ∠DBA + 80°

⇒ ∠DBA = 110° - 80° = 30°.

Sum of angles of a triangle = 180°

In △DAB,

⇒ ∠DAB + ∠DBA + ∠ADB = 180°

⇒ 70° + 30° + ∠ADB = 180°

⇒ ∠ADB = 180° - 100° = 80°.

Since, opposite angles of a parallelogram are equal,

∴ ∠C = ∠A = 70°.

In △DBC,

⇒ ∠DBC + ∠BCD + ∠CDB = 180°

⇒ 80° + 70° + ∠CDB = 180°

⇒ ∠CDB = 180° - 150° = 30°.

Hence, ∠ADB = 80° and ∠CDB = 30°.

In figure (2) given below, ABCD is a parallelogram. Find the angles of △AOD.

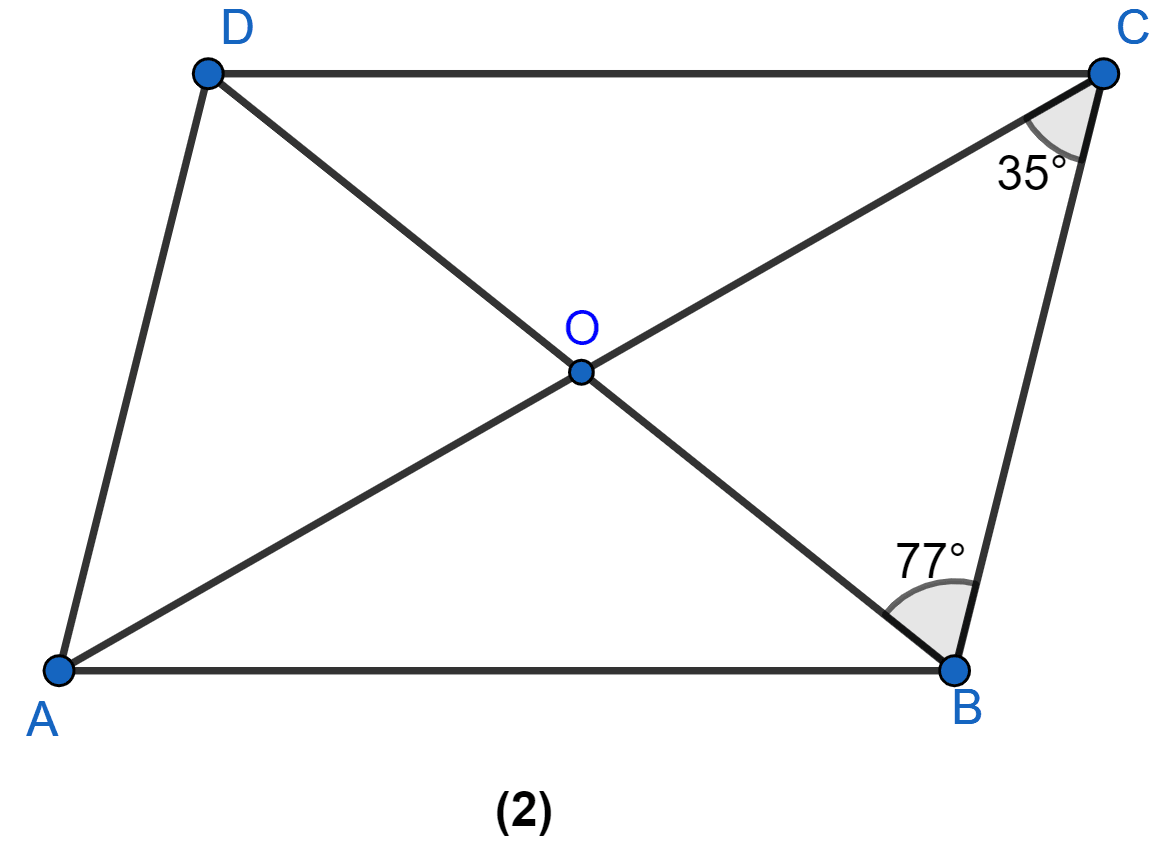
Answer

Sum of angles of a triangle = 180°

In △BOC,

⇒ ∠BOC + ∠OCB + ∠CBO = 180°

⇒ ∠BOC + 35° + 77° = 180°

⇒ ∠BOC = 180° - 35° - 77° = 68°.

From figure,

∠AOD = ∠BOC = 68° (Vertically opposite angles are equal)

∠OAD = ∠OCB = 35° (Alternate angles are equal)

∠ADO = ∠CBO = 77° (Alternate angles are equal)

Hence, ∠AOD = 68°, ∠OAD = 35°, ∠ADO = 77°.

In figure (3) given below, ABCD is a rhombus. Find the value of x.

Answer

As AD || BC, sum of co-int ∠s = 180°.

∠A + ∠B = 180°

∠B = 180° - ∠A = 180° - 72° = 108°.

The diagonals of rhombus bisect the angles.

$\therefore x° = \dfrac{1}{2} \times 108° = 54°.$

⇒ x = 54.

Hence, x = 54.

In figure (1) given below, ABCD is a parallelogram with perimeter 40. Find the values of x and y.

Answer

In parallelogram opposite sides are equal.

∴ BC = AD = 2x and

AB = CD

⇒ 3x = 2y + 2

⇒ 2y = 3x - 2

⇒ y = $\dfrac{3x - 2}{2}$ ........(i)

Given, perimeter = 40.

⇒ AB + BC + CD + AD = 40

⇒ 3x + 2x + 2y + 2 + 2x = 40

⇒ 3x + 2x + $2\Big(\dfrac{3x - 2}{2}\Big)$ + 2 + 2x = 40

⇒ 3x + 2x + 3x - 2 + 2 + 2x = 40

⇒ 10x = 40

⇒ x = 4.

⇒ y = $\dfrac{3x - 2}{2} = \dfrac{3 \times 4 - 2}{2} = \dfrac{12 - 2}{2} = 5$.

Hence, x = 4 and y = 5.

In figure (2) given below, ABCD is a parallelogram. Find the values of x and y.

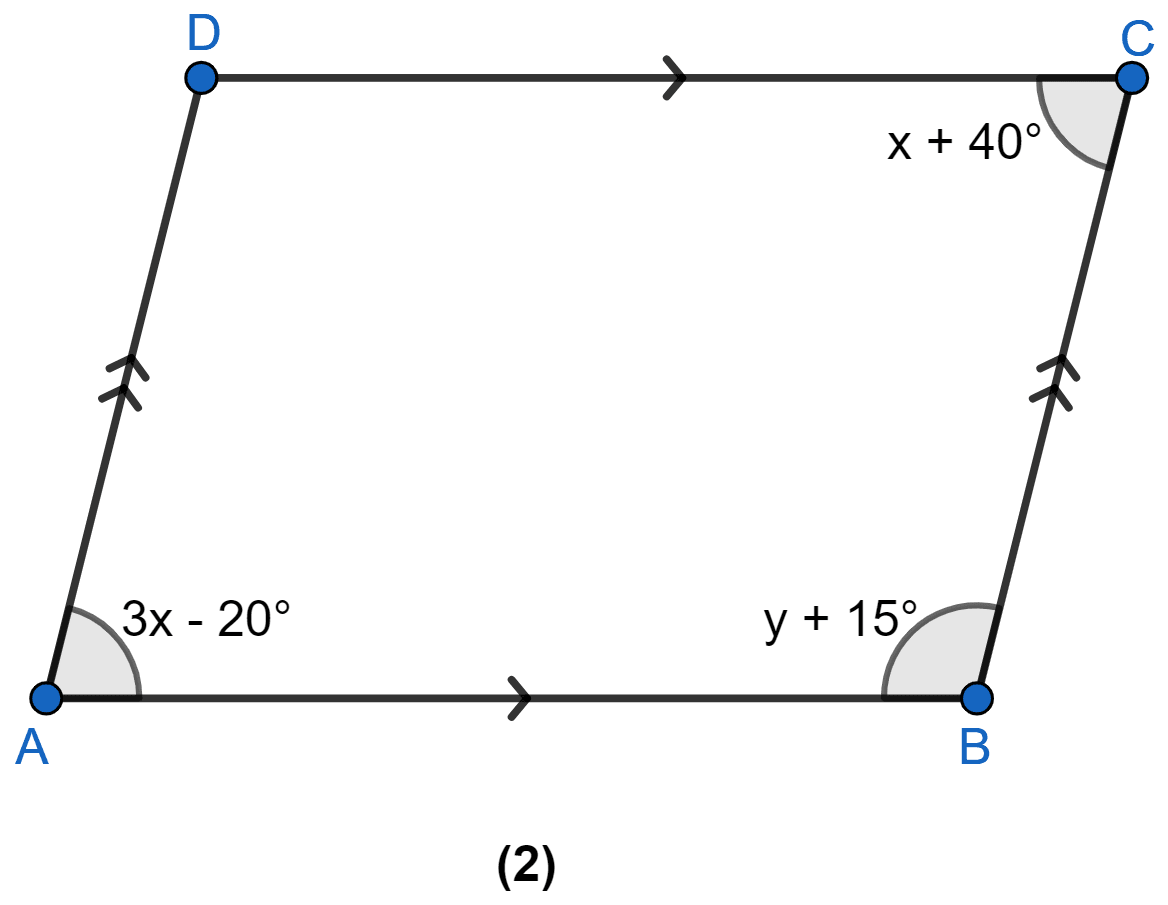
Answer

In parallelogram,

Opposite angles are equal

∴ ∠A = ∠C

⇒ 3x - 20° = x + 40°

⇒ 3x - x = 40° + 20°

⇒ 2x = 60°

⇒ x = 30°.

As AD || BC, sum of co-int ∠s = 180°.

⇒ ∠A + ∠B = 180°

⇒ 3x - 20° + y + 15° = 180°

⇒ 3(30°) - 20° + y + 15° = 180°

⇒ 90° - 20° + y + 15° = 180°

⇒ 85° + y = 180°

⇒ y = 95°.

Hence, x = 30° and y = 95°.

In figure (3) given below, ABCD is a rhombus. Find x and y.

Answer

Sides of rhombus are equal.

∴ AB = AD

⇒ 4x - 4 = 3x + 2

⇒ 4x - 3x = 2 + 4

⇒ x = 6.

AB = 3x + 2 = 3(6) + 2 = 20.

In △ABD,

AB = AD

so, ∠D = ∠B (Angles opposite to equal sides are equal in isosceles triangle)

Let angle be ∠D = ∠B = a

So,

⇒ ∠A + ∠D + ∠B = 180°

⇒ 60° + a + a = 180°

⇒ 2a = 180° - 60°

⇒ 2a = 120°

⇒ a = 60°.

Hence, △ABD is an equilateral triangle, so all sides are equal.

⇒ BD = AB

⇒ y - 1 = 20

⇒ y = 21.

Hence x = 6 and y = 21.

The diagonals AC and BD of a rectangle ABCD intersect each other at P. If ∠ABD = 50°, find ∠DPC.

Answer

The diagonals of a rectangle are equal and bisect each other.

∴ AP = BP

From figure,

In △ABP,

AP = BP

⇒ ∠PAB = ∠ABP = 50° (Angles opposite to equal sides are equal in isosceles triangle)

⇒ ∠PAB + ∠ABP + ∠APB = 180°

⇒ 50° + 50° + ∠APB = 180°

⇒ ∠APB = 180° - 100° = 80°.

⇒ ∠DPC = ∠APB = 80° (Vertically opposite angles are equal).

Hence, ∠DPC = 80°.

In figure (1) given below, equilateral triangle EBC surmounts square square ABCD. Find angle BED represented by x.

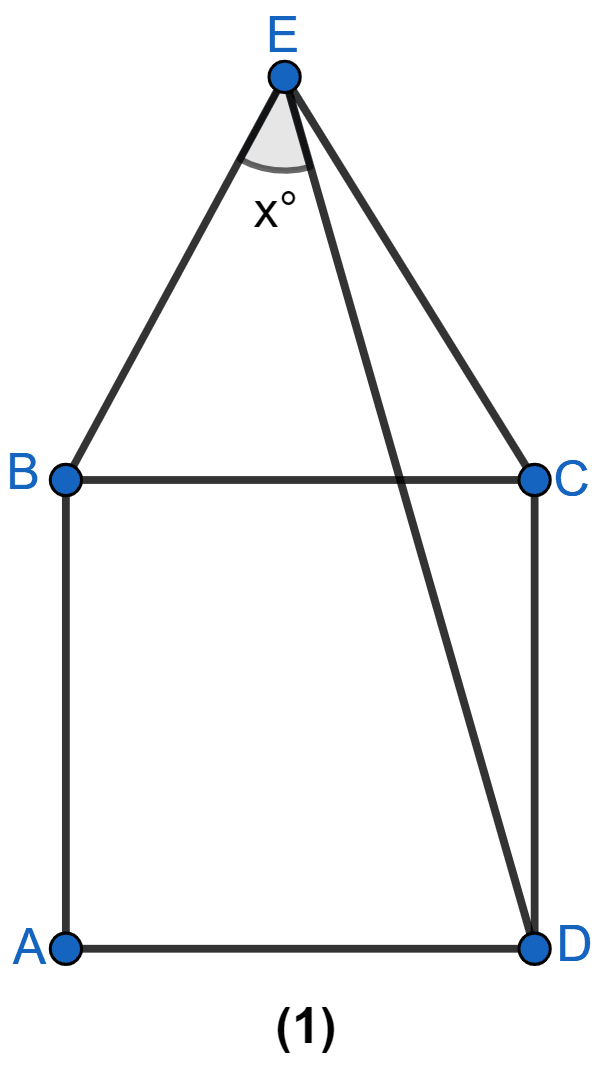
Answer

△EBC is an equilateral triangle, so all sides are equal.

EB = BC = EC ........(i)

In square all sides are equal

AD = CD = BC = AB ........(ii)

From (i) and (ii) we get,

BC = EC = CD

⇒ EC = CD.

In △ECD,

EC = CD

⇒ ∠DEC = ∠CDE = a (let) (Angles opposite to equal sides are equal in isosceles triangle)

⇒ ∠C = ∠ECB + ∠BCD

∠ECB = 60° (As each angle of a equilateral triangle = 60°)

∠BCD = 90° (As each angle of a square = 90°)

⇒ ∠C = 60° + 90° = 150°.

⇒ ∠DEC + ∠CDE + ∠C = 180

⇒ a + a + 150° = 180°

⇒ 2a = 180° - 150°

⇒ 2a = 30°

⇒ a = 15°.

From figure,

x° = ∠BEC - ∠DEC = 60° - 15° = 45°.

Hence, x = 45.

In Figure (2) given below, ABCD is a rectangle and diagonals intersect at O. AC is produced to E. If ∠ECD = 146°, find the angles of △AOB.

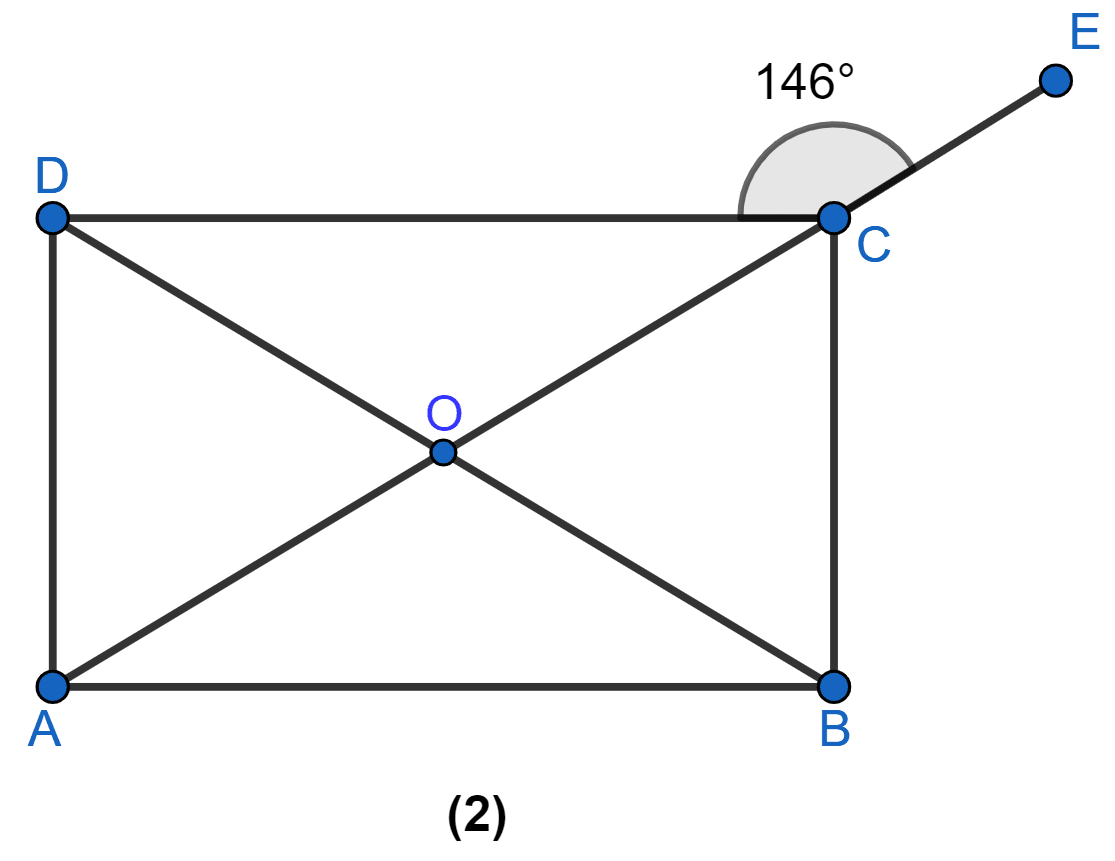
Answer

From figure,

∠OCD = 180° - 146° = 34° (As AE is a straight line).

The diagonals of a rectangle are equal and bisect each other.

∴ OC = OD

From figure,

In △OCD,

OC = OD

⇒ ∠ODC = ∠OCD = 34° (Angles opposite to equal sides are equal in isosceles triangle)

⇒ ∠ODC + ∠OCD + ∠DOC = 180°

⇒ 34° + 34° + ∠DOC = 180°

⇒ ∠DOC = 180° - 68° = 112°.

In △AOB,

⇒ ∠AOB = ∠DOC = 112° (Vertically opposite angles are equal).

⇒ ∠OAB = ∠OCD = 34°

⇒ ∠OBA = ∠ODC = 34°

Hence, ∠AOB = 112°, ∠OAB = 34° and ∠OBA = 34°.

In figure (3) given below, ABCD is a rhombus and diagonals intersect at O. If ∠OAB : ∠OBA = 3 : 2, find the angles of the △AOD.

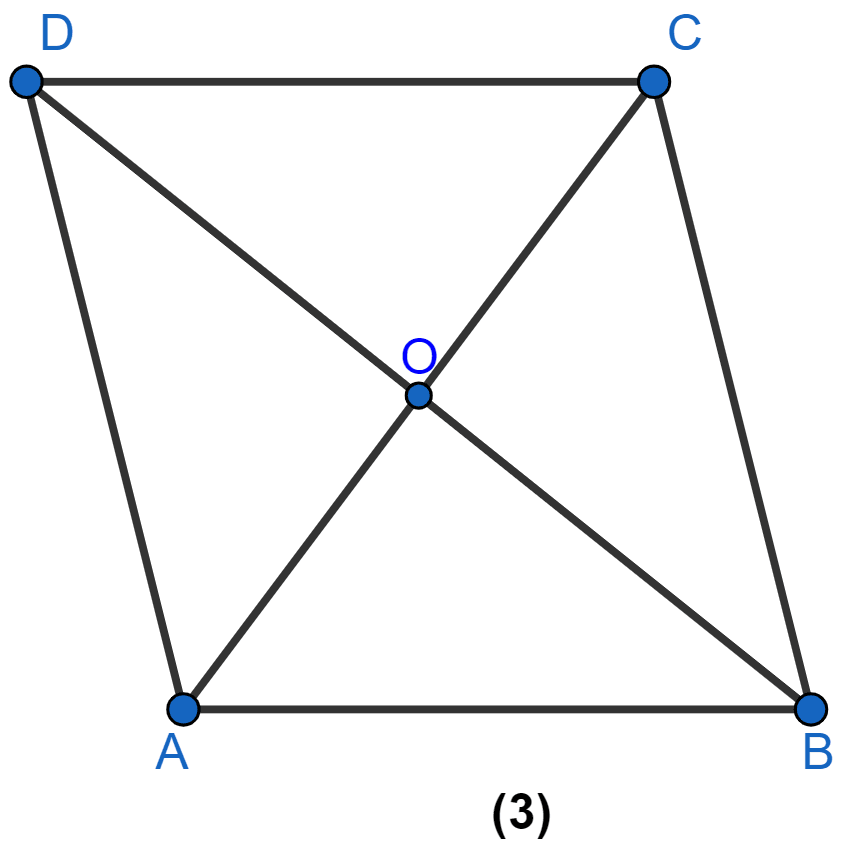
Answer

Let ∠OAB = 3x and ∠OBA = 2x.

The diagonals of rhombus are perpendicular to each other.

∴ ∠AOB = 90°

In △AOB,

⇒ ∠AOB + ∠OAB + ∠OBA = 180°

⇒ 90° + 3x + 2x = 180°

⇒ 5x = 90°

⇒ x = $\dfrac{90°}{5}$

⇒ x = 18°.

∠OAB = 3x = 3(18°) = 54°.

∠OBA = 2x = 2(18°) = 36°.

Since, diagonals of rhombus bisect vertex angles.

∴ ∠OAD = ∠OAB = 54°,

∠AOD = 90° (The diagonals of rhombus are perpendicular to each other.)

In △AOD,

⇒ ∠AOD + ∠OAD + ∠ODA = 180°

⇒ 90° + 54° + ∠ODA = 180°

⇒ ∠ODA + 144° = 180°

⇒ ∠ODA = 180° - 144°

⇒ ∠ODA = 36°.

Hence, ∠ODA = 36°, ∠OAD = 54°, ∠AOD = 90°.

In figure (1) given below, ABCD is a trapezium. Find the values of x and y.

Answer

Sum of adjacent co-interior angles of a trapezium = 180° (As AB || DC)

∴ ∠A + ∠D = 180°

⇒ x + 20° + 2x + 10° = 180°

⇒ 3x + 30° = 180°

⇒ 3x = 150°

⇒ x = $\dfrac{150°}{3}$

⇒ x = 50°.

∴ ∠B + ∠C = 180°

⇒ 92° + y = 180°

⇒ y = 180° - 92° = 88°.

Hence, x = 50° and y = 88°.

In figure (2) given below, ABCD is an isosceles trapezium. Find the values of x and y.

Answer

Sum of adjacent co-interior angles of a trapezium = 180° (As AB || DC)

∴ ∠A + ∠D = 180°

⇒ 2x + 3x = 180°

⇒ 5x = 180°

⇒ x = $\dfrac{180°}{5}$

⇒ x = 36°.

Opposite angles sum of a isosceles trapezium = 180°

∴ ∠A + ∠C = 180°

⇒ 2x + y = 180°

⇒ 2(36°) + y = 180°

⇒ 72° + y = 180°

⇒ y = 108°.

Hence, x = 36° and y = 108°.

In figure (3) given below, ABCD is a kite and diagonals intersect at O. If ∠DAB = 112° and ∠DCB = 64°, find ∠ODC and ∠OBA.

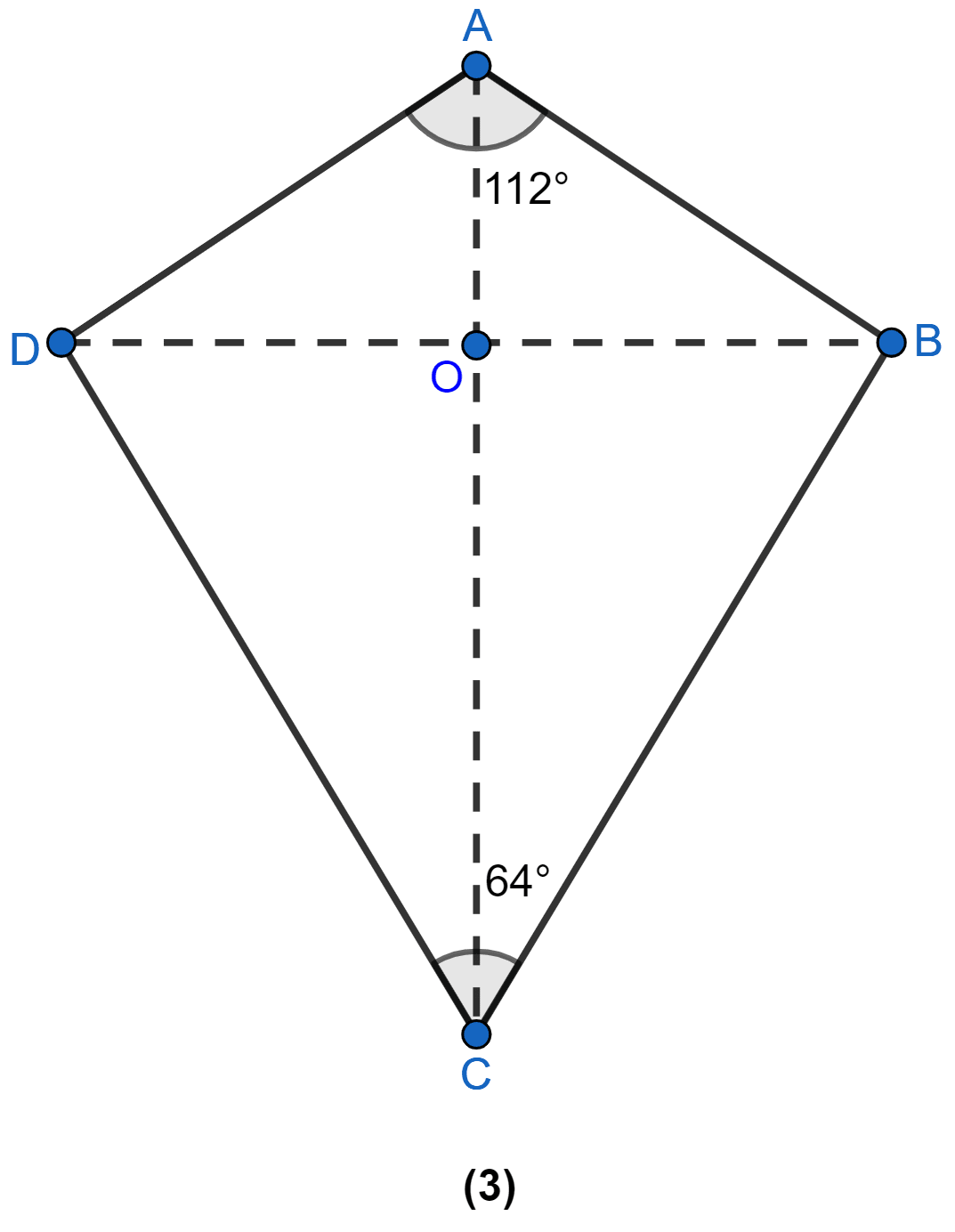
Answer

Diagonals of a kite bisect the vertex angles.

∴ ∠OCD = $\dfrac{∠C}{2} = \dfrac{64}{2}$ = 32° and ∠OAB = $\dfrac{∠A}{2} = \dfrac{112}{2}$ = 56°

Diagonals of a kite are perpendicular to each other.

∴ ∠DOC = 90°

⇒ ∠OCD + ∠DOC + ∠ODC = 180°

⇒ 32° + 90° + ∠ODC = 180°

⇒ ∠ODC = 58°.

Diagonals of a kite are perpendicular to each other.

∴ ∠AOB = 90°

⇒ ∠AOB + ∠OAB + ∠OBA = 180°

⇒ 90° + 56° + ∠OBA = 180°

⇒ ∠OBA = 180° - 146° = 34°.

Hence, ∠OBA = 34° and ∠ODC = 58°.

Prove that each angle of a rectangle is 90°.

Answer

We know that opposite sides of a rectangle are equal.

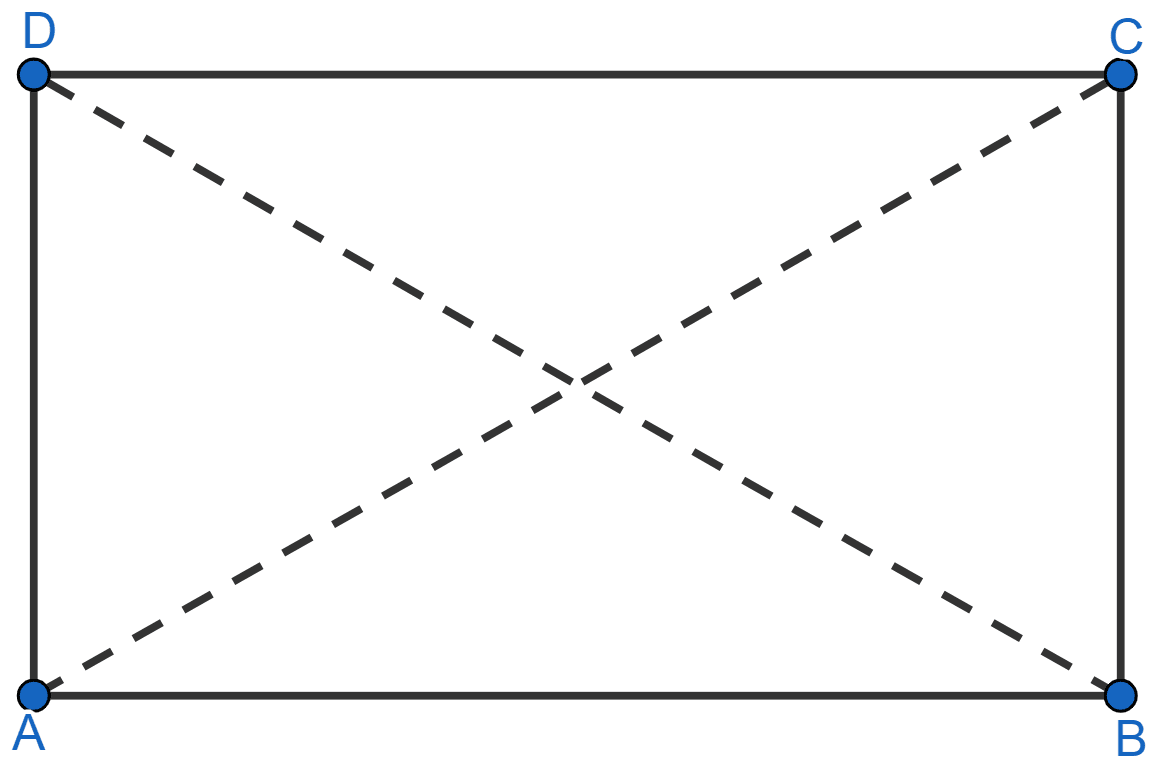
∴ AD = BC and AB = CD

Also, the diagonals of rectangle are equal.

∴ AC = BD

Now, consider ΔADC and ΔBCD

⇒ AD = BC

⇒ AC = BD

⇒ DC = DC [Common]

∴ ΔADC ≅ ΔBCD by SSS congruency rule.

∴ ∠ ADC = ∠BCD = x (let) [By C.P.C.T.]

But, adjacent sides of a parallelogram are supplementary. [∵ rectangle is a parallelogram].

∴ ∠ADC + ∠BCD = 180°

⇒ x + x = 180°

⇒ 2x = 180°

⇒ x = 90°

⇒ ∠ADC = ∠BCD = 90°.

Since, opposite angles of a parallelogram are also equal.

∴ ∠DAB = ∠BCD = 90° and ∠ABC = ∠ADC = 90°.

Hence, proved that each angle of a rectangle is 90°.

If the angle of a quadrilateral are equal, prove that it is a rectangle.

Answer

Suppose there is a quadrilateral ABCD.

Let ∠A = ∠B = ∠C = ∠D = x

So, ∠A = ∠C and ∠B = ∠D (Opposite angles are equal)

∴ ABCD is a parallelogram.

Since, sum of angles in a quadrilateral = 360°

⇒ ∠A + ∠B + ∠C + ∠D = 360°

⇒ x + x + x + x = 360°

⇒ 4x = 360°

x = $\dfrac{360°}{4}$

⇒ x = 90°.

∴ ∠A = ∠B = ∠C = ∠D = 90°.

Since, each angle = 90°,

Hence, proved that ABCD is a rectangle.

If the diagonals of a rhombus are equal, prove that it is a square.

Answer

From figure,

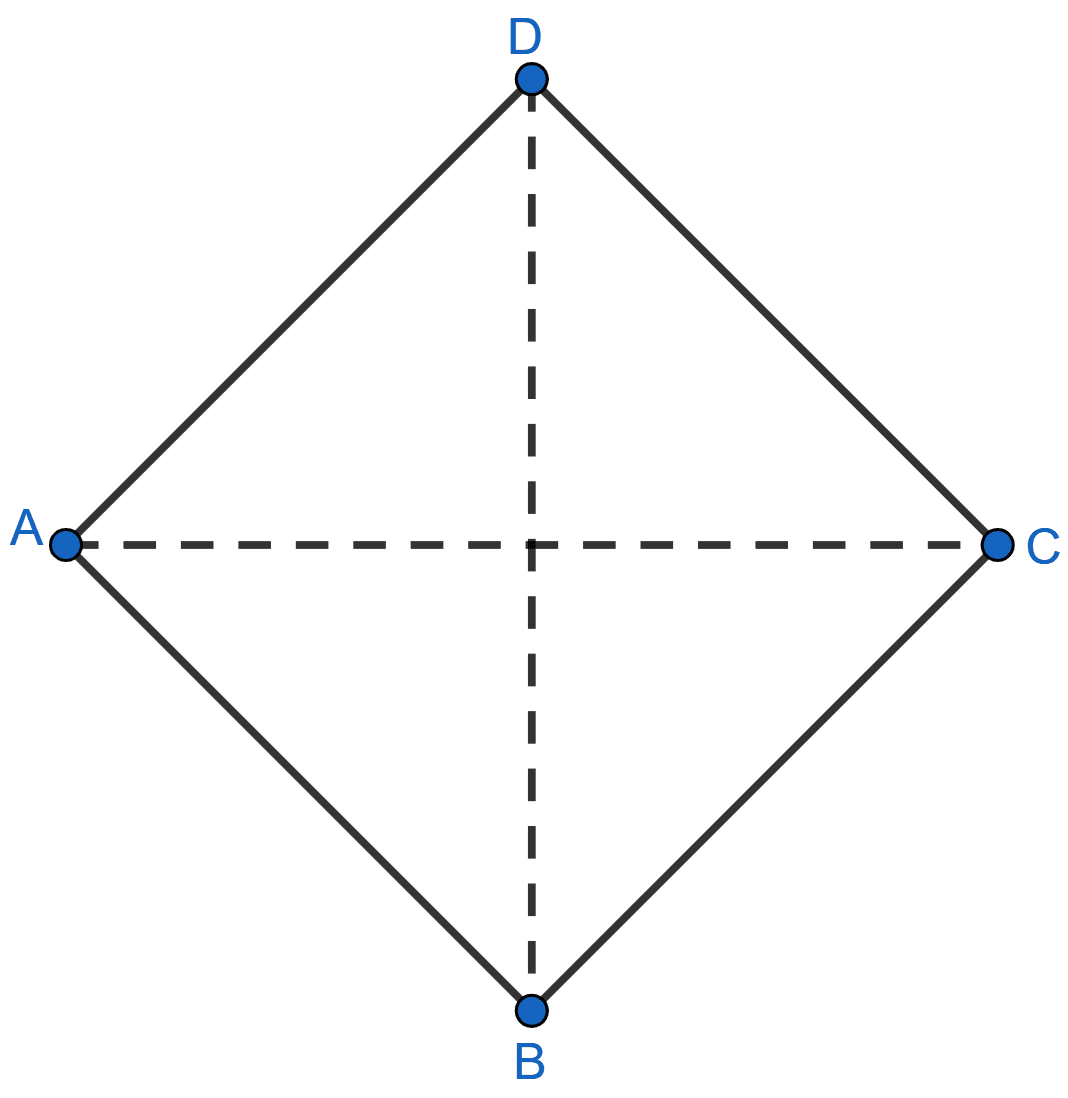
In △ABC and △BCD,

AB = DC (All sides of rhombus are equal)

BC = BC (Common sides)

AC = BD (Given diagonals are equal)

∴ △ABC ≅ △BCD (By SSS rule of congruency)

∠ABC = ∠BCD = x (let) (By C.P.C.T.)

∠ABC + ∠DCB = 180° [∵ AB || DC, sum of co-int ∠s = 180°]

⇒ x + x = 180°

⇒ 2x = 180°

x = $\dfrac{180°}{2}$

⇒ x = 90°.

∴ ∠ABC = ∠DCB = 90°.

Hence, proved that ABCD is a square.

Prove that every diagonal of a rhombus bisects the angles at the vertices.

Answer

From figure,

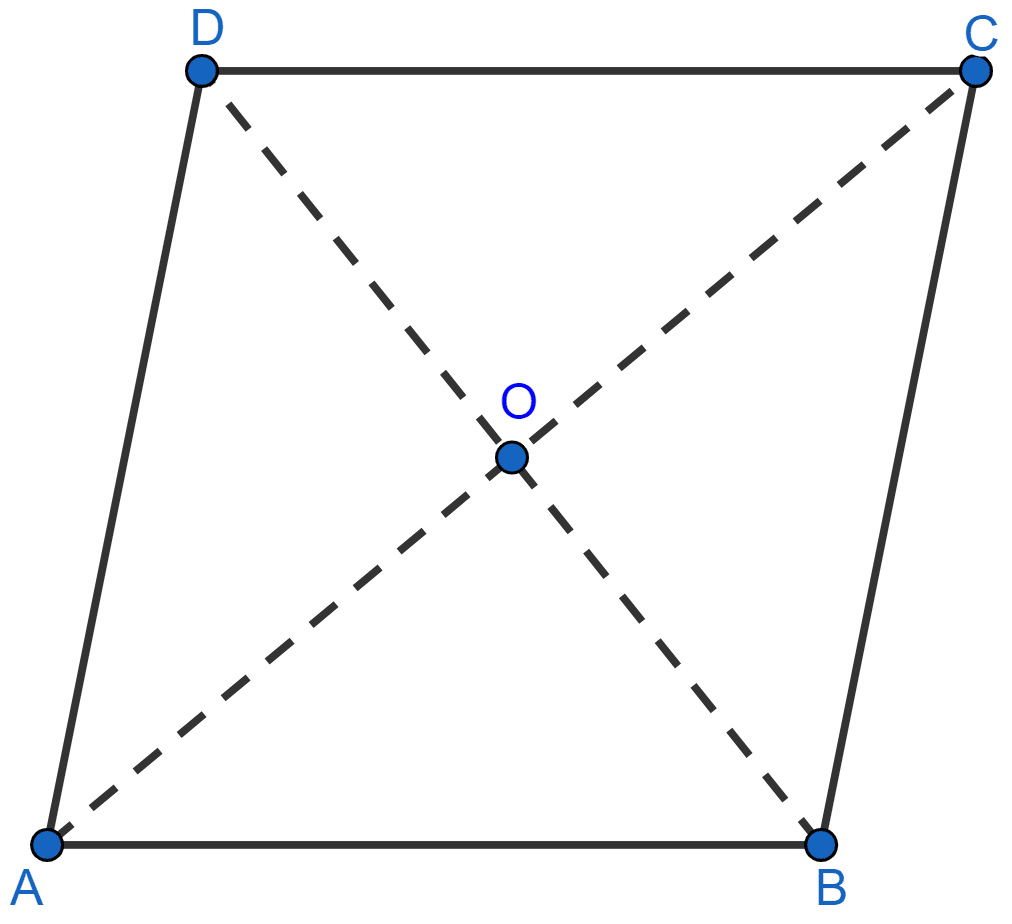
In △AOD and △COD,

AD = CD (All sides of rhombus are equal)

DO = OD (Common sides)

AO = OC (Diagonals of rhombus bisect each other)

∴ △AOD ≅ △COD (By SSS rule of congruency)

∴ ∠ADO = ∠CDO (By C.P.C.T.)

∴ BD bisects ∠D.

In △AOB and △COB,

AB = BC (All sides of rhombus are equal)

BO = OB (Common sides)

AO = OC (Diagonals of rhombus bisect each other)

∴ △AOB ≅ △COB (By SSS rule of congruency)

∴ ∠ABO = ∠CBO (By C.P.C.T.)

∴ BD bisects ∠B.

In △AOB and △AOD,

AB = AD (All sides of rhombus are equal)

AO = OA (Common sides)

OD = OB (Diagonals of rhombus bisect each other)

∴ △AOB ≅ △AOD (By SSS rule of congruency)

∴ ∠OAD = ∠OAB (By C.P.C.T.)

∴ AC bisects ∠A.

In △BOC and △DOC,

BC = CD (All sides of rhombus are equal)

OC = CO (Common sides)

OD = OB (Diagonals of rhombus bisect each other)

∴ △BOC ≅ △DOC (By SSS rule of congruency)

∴ ∠OCD = ∠OCB (By C.P.C.T.)

∴ AC bisects ∠C.

Hence, proved that every diagonal of a rhombus bisects the angles at the vertices.

ABCD is a parallelogram. If the diagonal AC bisects ∠A, then prove that :

(i) AC bisects ∠C

(ii) ABCD is a rhombus

(iii) AC ⊥ BD

Answer

Parallelogram ABCD is shown in the figure below:

(i) Given,

AC bisects ∠A,

∴ ∠CAB = ∠CAD = x (let) .......(i)

AB || CD (As opposite sides of parallelogram are parallel)

⇒ ∠DCA = ∠CAB (Alternate angles are equal)

∴ ∠DCA = x .......(ii)

and,

⇒ ∠BCA = ∠CAD (Alternate angles are equal)

∴ ∠BCA = x .......(iii)

From (i), (ii) and (iii) we get,

∠CAB = ∠CAD = ∠DCA = ∠BCA .......(iv)

Thus, ∠DCA = ∠BCA

Hence, proved that AC bisects ∠C.

(ii) From equation (iv) we get,

∠CAD = ∠DCA

∴ In △ADC,

DA = DC (Sides opposite to equal angles are equal)

However, DA = BC and AB = CD (opposite sides of a parallelogram are equal)

Thus, AB = BC = CD = DA

As ABCD is a parallelogram in which all sides are equal, therefore ABCD is a rhombus.

Hence, proved that ABCD is a rhombus.

(iii) In △OAB and △OCB,

OA = OC (Diagonals of a parallelogram bisect each other)

OB = OB (Common Side)

AB = BC (Sides of Rhombus)

∴ △OAB ≅ △OCB (SSS rule of congruency)

∴ ∠AOB = ∠BOC (c.p.c.t)

But ∠AOB + ∠BOC = 180°

⇒ ∠AOB + ∠AOB = 180°

⇒ ∠AOB = $\dfrac{180°}{2}$

⇒ ∠AOB = 90°

∴ AC ⊥ BD

Hence, proved that AC ⊥ BD.

Prove that bisectors of any two adjacent angles of a parallelogram are at right angles.

Answer

Let AC be bisector of ∠A and BD be bisector of ∠B and they meet at point M.

From figure,

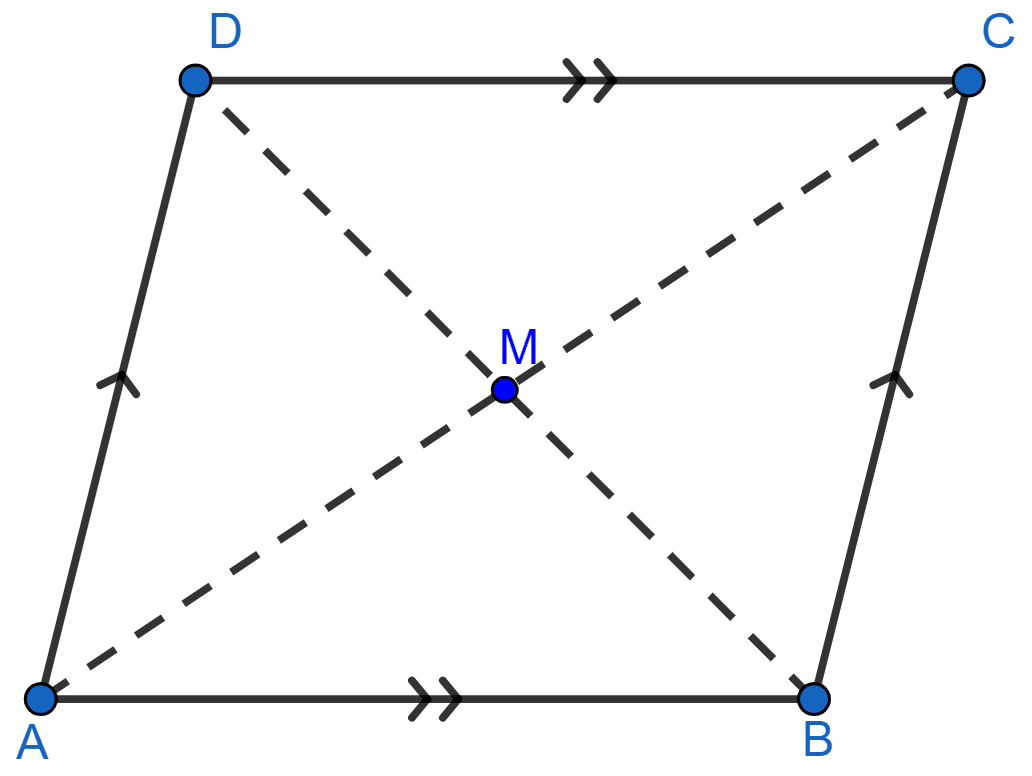
⇒ ∠A + ∠B = 180° (As AD || BC, sum of co-int ∠s = 180°)

⇒ $\dfrac{∠A + ∠B}{2} = \dfrac{180°}{2} = 90.$

⇒ $\dfrac{∠A}{2} + \dfrac{∠B}{2} = 90°$

∴ ∠MAB + ∠MBA = 90° .......(i)

In △MAB,

⇒ ∠MAB + ∠MBA + ∠AMB = 180° (Sum of angles of triangle = 180°)

⇒ 90° + ∠AMB = 180° (from i)

⇒ ∠AMB = 180° - 90°

⇒ ∠AMB = 90°.

Hence, proved that bisectors of any two adjacent angles of a parallelogram are at right angles.

Prove that bisectors of any two opposite angles of a parallelogram are parallel.

Answer

Let the parallelogram be ABCD as shown in the figure below:

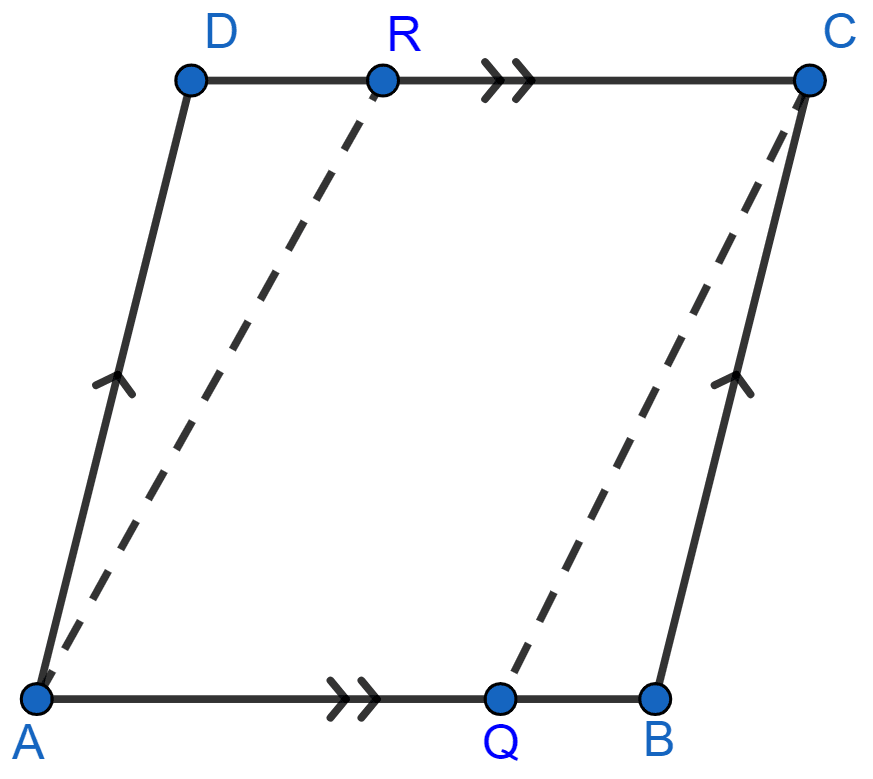
In parallelogram ABCD we have,

∠A = ∠C (Opposite angles are equal)

so,

$\dfrac{∠A}{2} = \dfrac{∠C}{2}$

∠DAR = ∠QCB (As AR bisects ∠A and QC bisects ∠C and ∠A = ∠C)

In △ADR and △CBQ,

⇒ ∠DAR = ∠QCB (Proved above)

⇒ AD = BC (Opposite sides of a || gm)

⇒ ∠D = ∠B (Opposite angles of a || gm)

Hence, △ADR ≅ △CBQ by ASA axiom.

∴ ∠DRA = ∠BQC (By C.P.C.T.) .......(i)

Also,

∠RAQ = ∠DRA (Alternate angles are equal) .........(ii)

From (i) and (ii) we get,

∠RAQ = ∠BQC (These are also corresponding angles)

Since, corresponding angles are equal, we can say that

AR || QC.

Hence, proved that bisectors of any two opposite angles of a parallelogram are parallel.

If the diagonals of a quadrilateral are equal and bisect each other at right angles, then prove that it is a square.

Answer

Since, diagonals bisect each other at 90°

∴ ∠AOB = ∠COD = ∠BOC = AOD = 90°.

From figure,

Considering △OAB and △ODC we have,

⇒ OA = OC (As diagonals bisect each other)

⇒ OB = OD (As diagonals bisect each other)

⇒ ∠AOB = ∠COD (Vertically opposite angles are equal)

Hence, △OAB ≅ △ODC by SAS axiom.

AB = CD (By C.P.C.T.) .........(i)

∴ ∠OAB = ∠OCD (By C.P.C.T.)

The above angles are alternate angles.

Hence, we can say that AB || CD.

In △AOB,

OA = OB (As both diagonals are equal and bisect each other)

so,

⇒ ∠OBA = ∠OAB = x (let) (Angles opposite to equal sides are equal in isosceles triangle)

⇒ ∠OBA + ∠OAB + ∠AOB = 180°

⇒ x + x + 90° = 180°

⇒ 2x = 180° - 90°

⇒ 2x = 90°

⇒ x = $\dfrac{90°}{2}$

⇒ x = 45°

Considering △OAD and △OBC we have,

⇒ OA = OC (As diagonals bisect each other)

⇒ OB = OD (As diagonals bisect each other)

⇒ ∠AOD = ∠COB (Vertically opposite angles are equal)

Hence, △OAD ≅ △OBC by SAS axiom.

AD = BC (By C.P.C.T.) .........(ii)

∠OAD = ∠OCB (By C.P.C.T.)

Hence, we can say that AD || BC.

Considering △AOB and △AOD we have,

⇒ AO = AO (Common sides)

⇒ OB = OD (As diagonals bisect each other)

⇒ ∠AOD = ∠AOB (Both equal to 90°)

Hence, △AOB ≅ △AOD by SAS axiom.

AB = AD (By C.P.C.T.) .........(iii)

From (i), (ii) and (iii) we get,

AB = BC = CD = AD.

In △AOD,

OA = OD (As both diagonals are equal and bisect each other)

so,

⇒ ∠OAD = ∠ODA = a (let) (Angles opposite to equal sides are equal in isosceles triangle)

⇒ ∠OAD + ∠ODA + ∠AOD = 180°

⇒ a + a + 90° = 180°

⇒ 2a = 180° - 90°

⇒ 2a = 90°

⇒ a = $\dfrac{90°}{2}$

⇒ a = 45°.

∠A = ∠OAB + OAD = 45° + 45° = 90°.

Thus, AB ⊥ AD.

Since, AD || BC so, AB ⊥ BC.

Since, AB || CD and AB ⊥ AD,

∴ CD ⊥ AD.

Since, alternate sides are perpendicular and all sides are equal.

Hence, proved that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square

If ABCD is a parallelogram in which diagonal AC bisects ∠A, then prove that ABCD is a rhombus.

Answer

Parallelogram ABCD is shown in the figure below:

Given,

AC bisects ∠A,

∴ ∠CAB = ∠CAD = x (let) ....................(1)

AB || CD (As opposite sides of parallelogram are parallel)

⇒ ∠DCA = ∠CAB (Alternate angles are equal)

∴ ∠DCA = x ....................(2)

and,

⇒ ∠BCA = ∠CAD (Alternate angles are equal)

∴ ∠BCA = x ....................(3)

From (1), (2) and (3) we get,

⇒ ∠CAB = ∠CAD = ∠DCA = ∠BCA ....................(4)

⇒ ∠CAD = ∠DCA

∴ In △ADC,

⇒ ∠CAD = ∠DCA

⇒ DA = DC (Sides opposite to equal angles in a triangle are equal) .........(5)

We know that,

Opposite sides of a parallelogram are equal.

AB = CD and BC = DA ...........(6)

From equation (5) and (6),

AB = BC = CD = DA

As ABCD is a parallelogram in which all sides are equal, therefore ABCD is a rhombus.

Hence, proved that ABCD is a rhombus.

If ABCD is a rectangle in which the diagonal BD bisects ∠B, then show that ABCD is a square.

Answer

Since, BD bisects ∠B.

∴ ∠1 = ∠2

Since, ∠B = 90°.

∠1 = ∠2 = 45°

∠4 = ∠1 = 45° (Alternate angles are equal)

∠3 = ∠2 = 45° (Alternate angles are equal)

In △ABD,

AB = AD (As sides opposite to equal angles are equal) .........(i)

In △CBD,

BC = CD (As sides opposite to equal angles are equal) ..........(ii)

and AD = BC, AB = CD (As opposite sides of rectangle are equal) .......(iii)

From (i), (ii) and (iii) we get,

AB = BC = CD = AD.

Since, all sides are equal and alternate sides are perpendicular to each other.

Hence, proved that ABCD is a square.

Show that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square.

Answer

Since, diagonals bisect each other at 90°

∴ ∠AOB = ∠COD = BOC = AOD = 90°.

From figure,

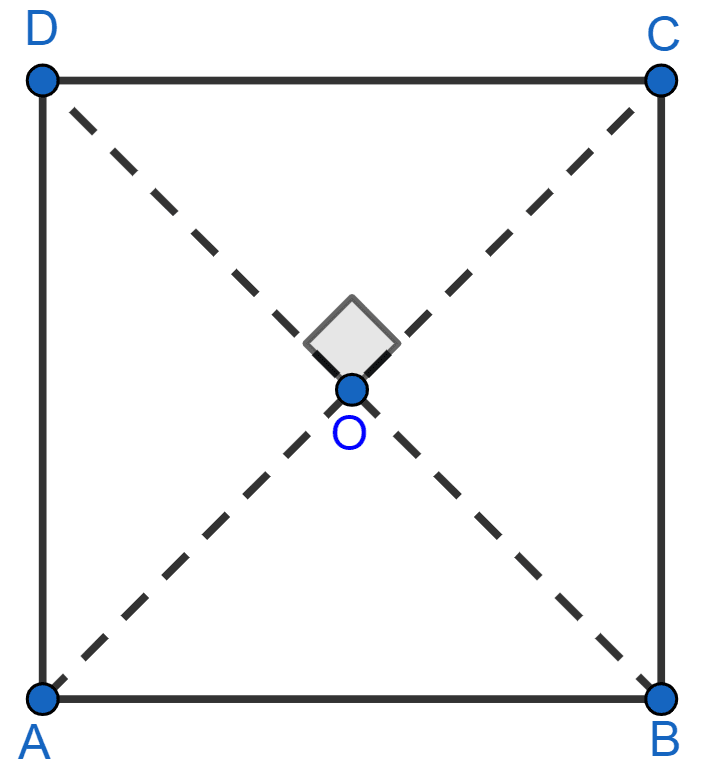
Considering △OAB and △ODC we have,

⇒ OA = OC (As diagonals bisect each other)

⇒ OB = OD (As diagonals bisect each other)

⇒ ∠AOB = ∠COD (Vertically opposite angles are equal)

Hence, △OAB ≅ △ODC by SAS axiom.

AB = CD (By C.P.C.T.) .........(i)

∴ ∠OAB = ∠OCD (By C.P.C.T.)

The above angles are alternate angles.

Hence, we can say that AB || CD.

In △AOB,

OA = OB (As both diagonals are equal and bisect each other)

so,

⇒ ∠OBA = ∠OAB = x (let) (Angles opposite to equal sides are equal in isosceles triangle)

⇒ ∠OBA + ∠OAB + ∠AOB = 180°

⇒ x + x + 90° = 180°

⇒ 2x = 180° - 90°

⇒ 2x = 90°

⇒ x = $\dfrac{90°}{2}$

⇒ x = 45°.

Considering △OAD and △OBC we have,

⇒ OA = OC (As diagonals bisect each other)

⇒ OB = OD (As diagonals bisect each other)

⇒ ∠AOD = ∠COB (Vertically opposite angles are equal)

Hence, △OAD ≅ △OBC by SAS axiom.

AD = BC (By C.P.C.T.) .........(ii)

∠OAD = ∠OCB (By C.P.C.T.)

Hence, we can say that AD || BC.

Considering △AOB and △AOD we have,

⇒ AO = AO (Common side)

⇒ OB = OD (As diagonals bisect each other)

⇒ ∠AOD = ∠AOB (Both equal to 90°)

Hence, △AOB ≅ △AOD by SAS axiom.

AB = AD (By C.P.C.T.) .........(iii)

From (i), (ii) and (iii) we get,

AB = BC = CD = AD.

In △AOD,

OA = OD (As both diagonals are equal and bisect each other)

so,

⇒ ∠OAD = ∠ODA = a (let) (Angles opposite to equal side are equal in isosceles triangle)

⇒ ∠OAD + ∠ODA + ∠AOD = 180°

⇒ a + a + 90° = 180°

⇒ 2a = 180° - 90°

⇒ 2a = 90°

⇒ a = $\dfrac{90°}{2}$

⇒ a = 45°.

∠A = ∠OAB + ∠OAD = 45° + 45° = 90°.

Thus, AB ⊥ AD.

Since, AD || BC so, AB ⊥ BC.

Since, AB || CD and AB ⊥ AD,

∴ CD ⊥ AD.

Since, alternate sides are perpendicular and all sides are equal.

Hence, proved that if the diagonals of a quadrilateral are equal and bisect each other at right angles, then it is a square

P and Q are points on opposite sides AD and BC of a parallelogram ABCD such that PQ passes through the point of intersection O of its diagonals AC and BD. Show that PQ is bisected at O.

Answer

Parallelogram ABCD is shown in the figure below:

Considering △OAP and △OCQ we have,

⇒ ∠OAP = ∠OCQ (Alternate angles are equal)

⇒ OA = OC (As diagonals bisect each other)

⇒ ∠AOP = ∠COQ (Vertically opposite angles)

Hence, △OAP ≅ △OCQ by ASA axiom.

OP = OQ (By C.P.C.T.)

Hence, proved that PQ is bisected at O.

In figure (1) given below, ABCD is a parallelogram and X is mid-point of BC. The line AX produced meets DC produced at Q. The parallelogram ABPQ is completed. Prove that

(i) the triangles ABX and QCX are congruent.

(ii) DC = CQ = QP

Answer

(i) Considering △ABX and △QCX we have,

⇒ ∠XAB = ∠XQC (Alternate angles are equal)

⇒ XB = XC (As X is mid-point of BC)

⇒ ∠AXB = ∠CXQ (Vertically opposite angles are equal)

Hence, △ABX ≅ △QCX by ASA axiom.

(ii) Since, △ABX ≅ △QCX

∴ AB = CQ (By C.P.C.T.) ..........(i)

AB = CD and AB = QP (Opposite sides of parallelogram are equal) .........(ii)

From (i) and (ii) we get,

⇒ AB = DC = CQ = QP

⇒ DC = CQ = QP

Hence, proved that DC = CQ = QP.

In figure (2) given below, points P and Q have been taken on opposite sides AB and CD respectively of a parallelogram ABCD such that AP = CQ. Show that AC and PQ bisect each other.

Answer

Considering △AOP and △COQ we have,

⇒ ∠OAP = ∠OCQ (Alternate angles are equal)

⇒ AP = QC (Given)

⇒ ∠AOP = ∠COQ (Vertically opposite angles are equal)

Hence, △AOP ≅ △COQ by ASA axiom.

∴ AO = OC and OP = OQ (By C.P.C.T.)

Hence, proved that AC and PQ bisect each other at point O.

ABCD is a square. A is joined to a point P on BC and D is joined to a point Q on AB. If AP = DQ, prove that AP and DQ are perpendicular to each other.

Answer

Square ABCD is shown in the figure below:

Considering △ABP and △ADQ we have,

⇒ ∠ABP = ∠DAQ = 90°

⇒ AP = DQ (Given)

⇒ AB = AD (Sides of square are equal)

Hence, △ABP ≅ △ADQ by RHS axiom.

⇒ ∠BAP = ∠ADQ (By C.P.C.T.) ........(i)

⇒ ∠BAD = 90° (Each angle of square = 90°)

⇒ ∠BAP + ∠PAD = 90°

Substituting value of ∠ADQ from (i) we get,

⇒ ∠ADQ + ∠PAD = 90° .........(ii)

From figure,

∠ADQ = ∠ADM

∠PAD = ∠MAD

Substituting above values in (ii) we get,

⇒ ∠ADM + ∠MAD = 90° .......(iii)

In △AMD,

⇒ ∠ADM + ∠MAD + ∠AMD = 180°

⇒ 90° + ∠AMD = 180° (From iii)

⇒ ∠AMD = 90°

∴ AP ⊥ DQ.

Hence, proved that AP ⊥ DQ.

If P and Q are points of trisection of the diagonal BD of a parallelogram ABCD, prove that CQ || AP.

Answer

Since, AB || CD (Opposite sides of parallelogram are parallel) and BD is transversal.

From figure,

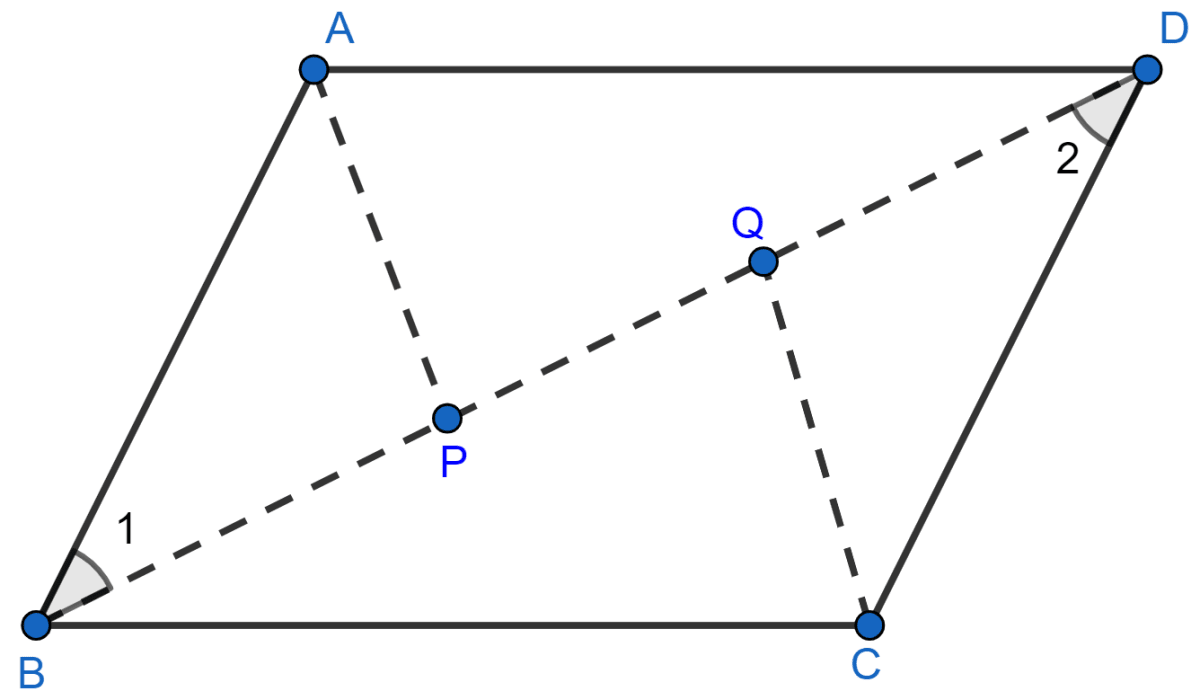
∠ABP = ∠CDQ (Alternate angles are equal)

BP = QD (As P and Q are points of trisection of the diagonal BD)

AB = CD (Opposite sides of parallelogram are equal)

Hence, △ABP ≅ △CDQ by SAS axiom.

∴ ∠APB = ∠CQD .......(By C.P.C.T.)

Multiplying both sides by -1

-∠APB = -∠CQD

Adding 180° on both sides,

⇒ 180° - ∠APB = 180° -∠CQD

⇒ ∠APQ = ∠CQP

The above angles are alternate angles and since they are equal we can say,

AP || CQ.

Hence, proved that AP || CQ.

A transversal cuts two parallel lines at A and B. The two interior angles at A are bisected and so are the two interior angles at B; the four bisectors form a quadrilateral ACBD. Prove that

(i) ACBD is a rectangle.

(ii) CD is parallel to the original parallel lines.

Answer

From figure,

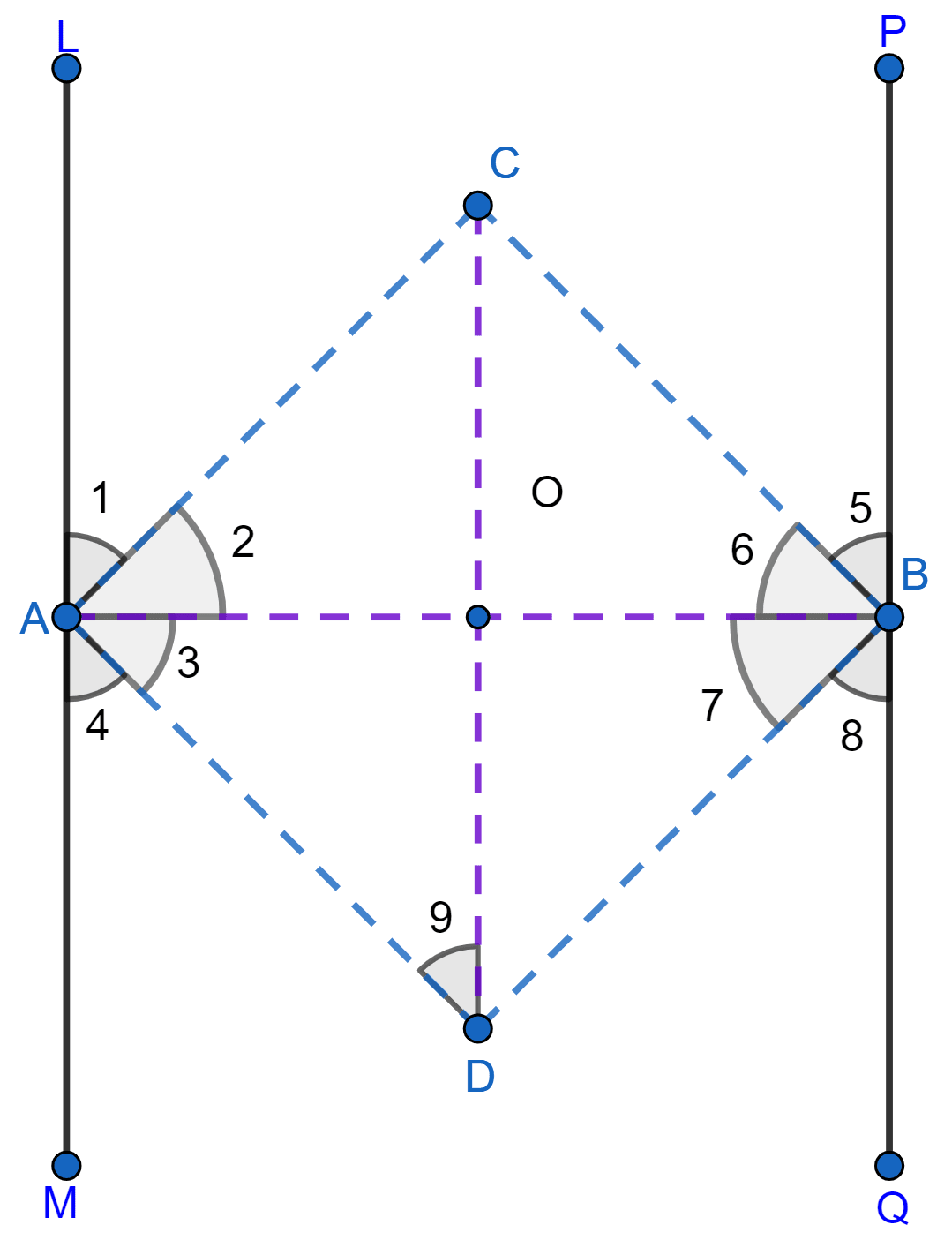
LM || PQ and AB is transversal.

AC, AD, BC and BD are bisectors of ∠LAB, ∠BAM, ∠PBA and ∠ABQ respectively.

So,

∠1 = ∠2, ∠3 = ∠4, ∠5 = ∠6 and ∠7 = ∠8.

(i) ∠LAB + ∠BAM = 180° (As LAM is a straight line)

$\dfrac{1}{2}$(∠LAB + ∠BAM) = $\dfrac{1}{2}$ x 180°

∠2 + ∠3 = 90° [Since, AC and AD are bisector of ∠LAB and ∠BAM]

∠CAD = 90°

∠A = 90°.

∠PBA + ∠QBA = 180° (As PBQ is a straight line)

$\dfrac{1}{2}$(∠PBA + ∠QBA) = $\dfrac{1}{2}$ x 180°

∠6 + ∠7 = 90° [Since, BC and BD are bisector of ∠PBA and ∠QBA]

∠CBD = 90°

∠B = 90°.

∠LAB + ∠ABP = 180° (LM || PQ, sum of co-interior angles is 180°)

$\dfrac{1}{2}$(∠LAB + ∠ABP) = $\dfrac{1}{2}$ x 180°

∠2 + ∠6 = 90° [Since, AC and BC are bisector of ∠LAB and ∠PBA]

In △ABC,

⇒ ∠2 + ∠6 + ∠C = 180°

⇒ 90° + ∠C = 180°

⇒ ∠C = 90°.

∠MAB + ∠ABQ = 180° (LM || PQ, sum of co-interior angles is 180°)

$\dfrac{1}{2}$(∠MAB + ∠ABQ) = $\dfrac{1}{2}$ x 180°

∠3 + ∠7 = 90° [Since, AD and BD are bisector of ∠MAB and ∠ABQ]

In △ABD,

⇒ ∠3 + ∠7 + ∠D = 180°

⇒ 90° + ∠D = 180°

⇒ ∠D = 90°.

From figure,

∠BAM = ∠ABP (Alternate angles are equal)

$\dfrac{∠\text{BAM}}{2} = \dfrac{∠\text{ABP}}{2}$

∠3 = ∠6

∠LAB = ∠ABQ (Alternate angles are equal)

$\dfrac{∠\text{LAB}}{2} = \dfrac{∠\text{ABQ}}{2}$

∠2 = ∠7

In △ABC and △ABD,

∠3 = ∠6 (Proved above)

∠2 = ∠7 (Proved above)

AB = AB (Common)

Hence, △ABC ≅ △ABD by ASA axiom.

∴ AD = BC and AC = BD (By C.P.C.T.)

Since, ∠A = ∠B = ∠C = ∠D = 90° and AD = BC, AC = BD.

Hence, proved that ACBD is a rectangle.

(ii) In △OAD,

OA = OD (Diagonals of rectangle bisect each other)

∠3 = ∠9 (Angles opposite to equal side are equal)

Since, ∠3 = 4,

∠9 = ∠4

Since, ∠9 and ∠4 are alternate angles and since they are equal we can say that,

⇒ OD || LM

⇒ CD || LM

Since, LM || PQ and CD || LM

⇒ CD || PQ.

Hence, proved that CD is parallel to the original parallel lines.

In parallelogram ABCD, the bisector of ∠A meets DC in E and AB = 2AD. Prove that

(i) BE bisects ∠B

(ii) ∠AEB = a right angle.

Answer

Parallelogram ABCD is shown in the figure below:

(i) AB = CD (Opposite sides of parallelogram are equal)

AD = BC (Opposite sides of parallelogram are equal)

From figure,

⇒ ∠1 = ∠2 (AE bisects ∠A)

⇒ ∠1 = ∠5 (Alternate angles are equal)

⇒ ∠2 = ∠5

⇒ AD = DE (As sides opposite to equal angles are equal)

Since, AB = 2AD and CD = AB

⇒ CD = 2AD

⇒ 2AD = DE + EC

⇒ 2AD = AD + EC

⇒ EC = AD.

Since, EC = AD and BC = AD

⇒ ∠6 = ∠4 (As angles opposite to equal sides are equal)

⇒ ∠6 = ∠3 (Alternate angles are equal)

∴ ∠3 = ∠4.

Since, ∠3 = ∠4, hence proved that BE bisects ∠B.

(ii) Let ∠1 = x and ∠3 = y.

∴ ∠2 = x and ∠4 = y

Since, AD || BC, sum of co-interior angles = 180

⇒ ∠A + ∠B = 180°

⇒ ∠1 + ∠2 + ∠3 + ∠4 = 180°

⇒ x + x + y + y = 180°

⇒ 2x + 2y = 180°

⇒ x + y = 90° ..........(1)

In △AEB,

⇒ ∠1 + ∠3 + ∠AEB = 180°

⇒ x + y + ∠AEB = 180°

⇒ 90° + ∠AEB = 180° (From i)

⇒ ∠AEB = 90°.

Hence, proved that ∠AEB = 90°.

ABCD is a parallelogram, bisectors of angles A and B meet at E which lies on DC. Prove that AB = 2AD.

Answer

ABCD is a parallelogram in which bisector of ∠A and ∠B meets DC at E.

To prove: AB = 2AD

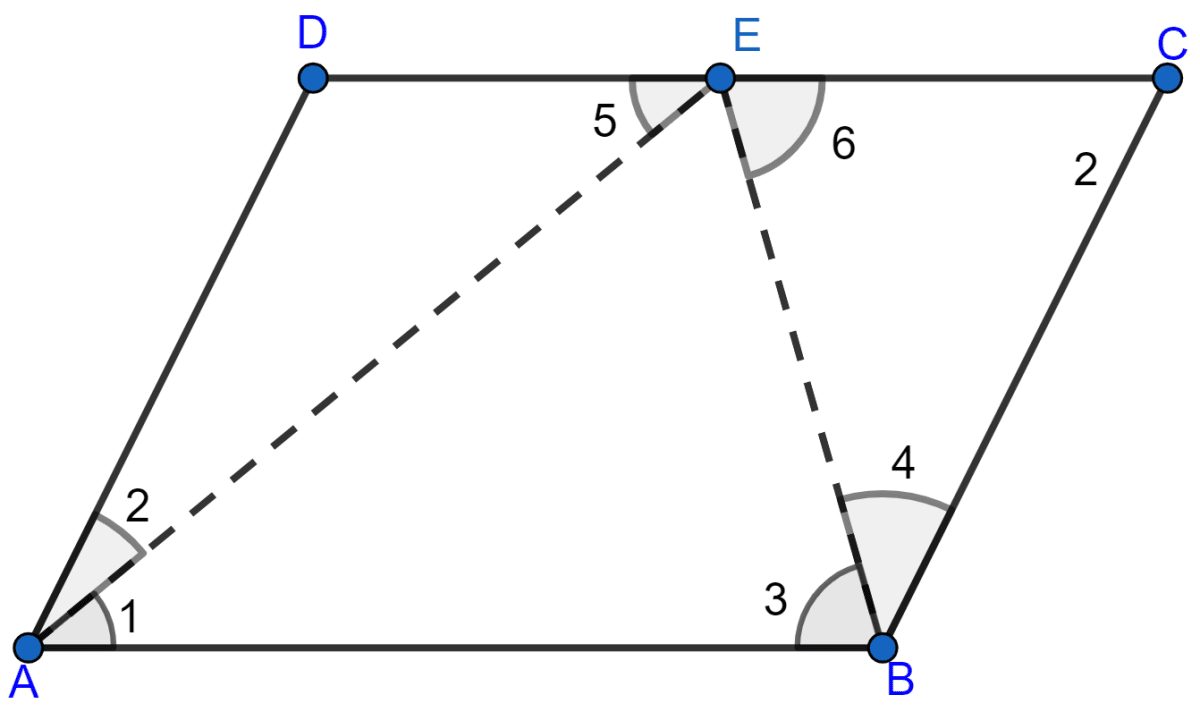
Since, AE and BE are bisector of ∠A and ∠B

∠1 = ∠2 and ∠3 = ∠4

In parallelogram ABCD, we have

AB || DC

∠1 = ∠5 [Alternate angles are equal, AE is transversal]

Thus,

∠2 = ∠5 … (i)

∴ DE = AD [∵ Sides opposite to equal angles in ∆AED]

∠3 = ∠6 [Alternate angles]

∠3 = ∠4 [Since, BE is bisector of ∠B (given)]

Thus, ∠4 = ∠6 … (ii)

∴ BC = EC [∵ Sides opposite to equal angles in ∆BCE]

AD = BC [Opposite sides of || gm are equal]

AD = DE = EC

AB = DC [Opposite sides of a || gm are equal]

⇒ AB = DE + EC

⇒ AB = AD + AD

⇒ AB = 2AD

Hence, proved that AB = 2AD.

ABCD is a square and the diagonals intersect at O. If P is a point on AB such that AO = AP, prove that 3∠POB = ∠AOP.

Answer

In square ABCD, AC is a diagonal.

So, ∠CAB = 45° (As diagonals bisect vertex angle)

∠OAP = 45°

In ∆AOP,

∠OAP = 45°

AO = AP [Given]

∠AOP = ∠APO = x (let) [Angles opposite to equal sides are equal]

Now,

∠AOP + ∠APO + ∠OAP = 180° [Angles sum property of a triangle]

∠AOP + ∠AOP + 45° = 180°

2x = 180° – 45°

x = $\dfrac{135°}{2}$

∠AOB = 90° [Diagonals of a square bisect at right angles]

So, ∠AOP + ∠POB = 90°

$\dfrac{135°}{2}$ + ∠POB = 90°

∠POB = 90° – $\dfrac{135°}{2}$

= $\dfrac{45°}{2}$

3∠POB = $3 \times \dfrac{45°}{2} = \dfrac{135°}{2}$ = ∠AOP.

Hence, proved that 3∠POB = ∠AOP.

ABCD is a square. E, F, G and H are points on the sides AB, BC, CD and DA respectively such that AE = BF = CG = DH. Prove that EFGH is a square.

Answer

Given, AE = BF = CG = DH

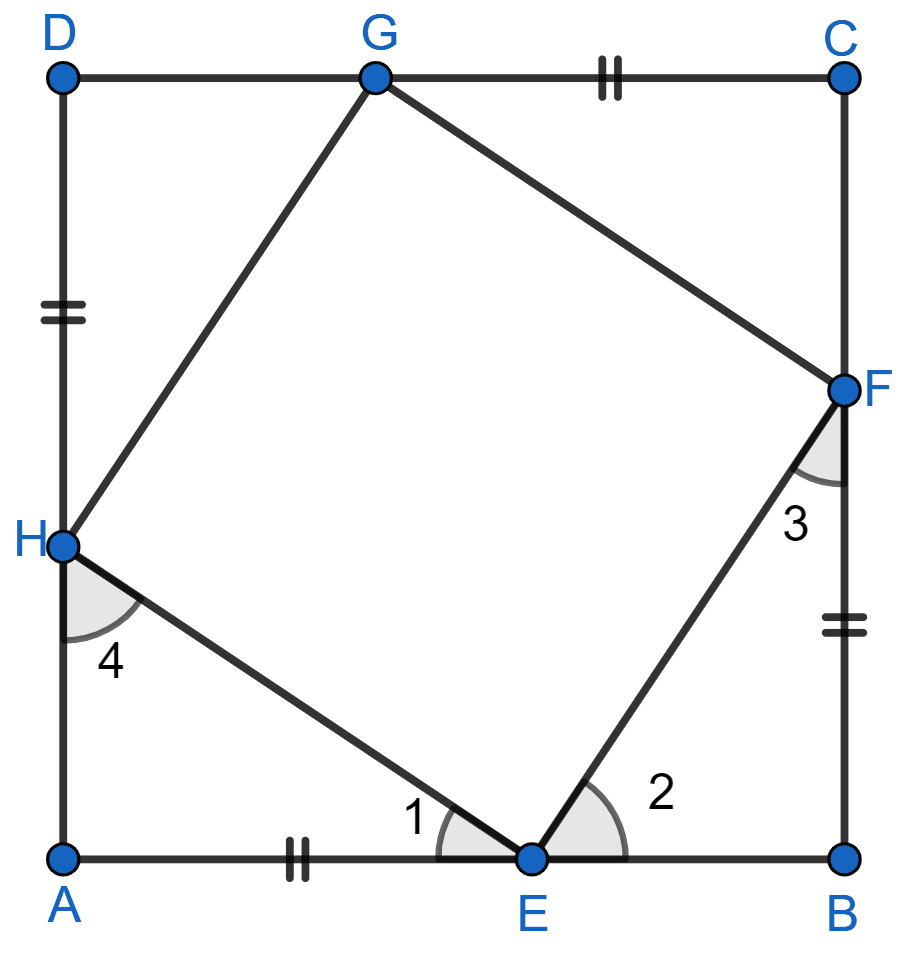
Since, ABCD is a square and AB = BC = CD = AD.

So,

⇒ AB - AE = BC - BF = CD - CG = AD - DH

⇒ EB = FC = GD = AH

Now, in ∆AEH and ∆BFE

⇒ AE = BF [Given]

⇒ AH = EB [Proved]

⇒ ∠A = ∠B [Each 90°]

So, ∆AEH ≅ ∆BFE by S.A.S axiom of congruency

Then, by C.P.C.T we have

⇒ EH = EF and ∠4 = ∠2

In ∆AEH,

⇒ ∠1 + ∠4 + ∠HAE = 180°

⇒ ∠1 + ∠4 + 90° = 180°

⇒ ∠1 + ∠4 = 90°

⇒ ∠1 + ∠2 = 90° [Since, ∠4 = ∠2]

From figure,

⇒ ∠1 + ∠HEF + ∠2 = 180°

⇒ ∠HEF + 90° = 180°

⇒ ∠HEF = ∠E = 90°.

In ∆DGH and ∆CGF

⇒ DH = GC [Given]

⇒ GD = FC [Proved]

⇒ ∠D = ∠C [Each 90°]

So, ∆DGH ≅ ∆CGF by S.A.S axiom of congruency

Then, by C.P.C.T we have

GH = FG

In ∆DGH and ∆AEH

⇒ DH = AE [Given]

⇒ GD = HA [Proved]

⇒ ∠D = ∠A [Each 90°]

So, ∆DGH ≅ ∆AEH by S.A.S axiom of congruency

Then, by C.P.C.T we have

GH = HE

Thus, EF = FG = GH = HE, therefore EFGH is a Rhombus.

∵ One angle of rhombus EFGH is 90° (∠HEF = 90°),

∴ EFGH is a square.

Hence, proved that EFGH is a square.

In the figure (1) given below, ABCD and ABEF are parallelograms. Prove that

(i) CDFE is a parallelogram.

(ii) FD = EC

(iii) △AFD ≅ △BEC.

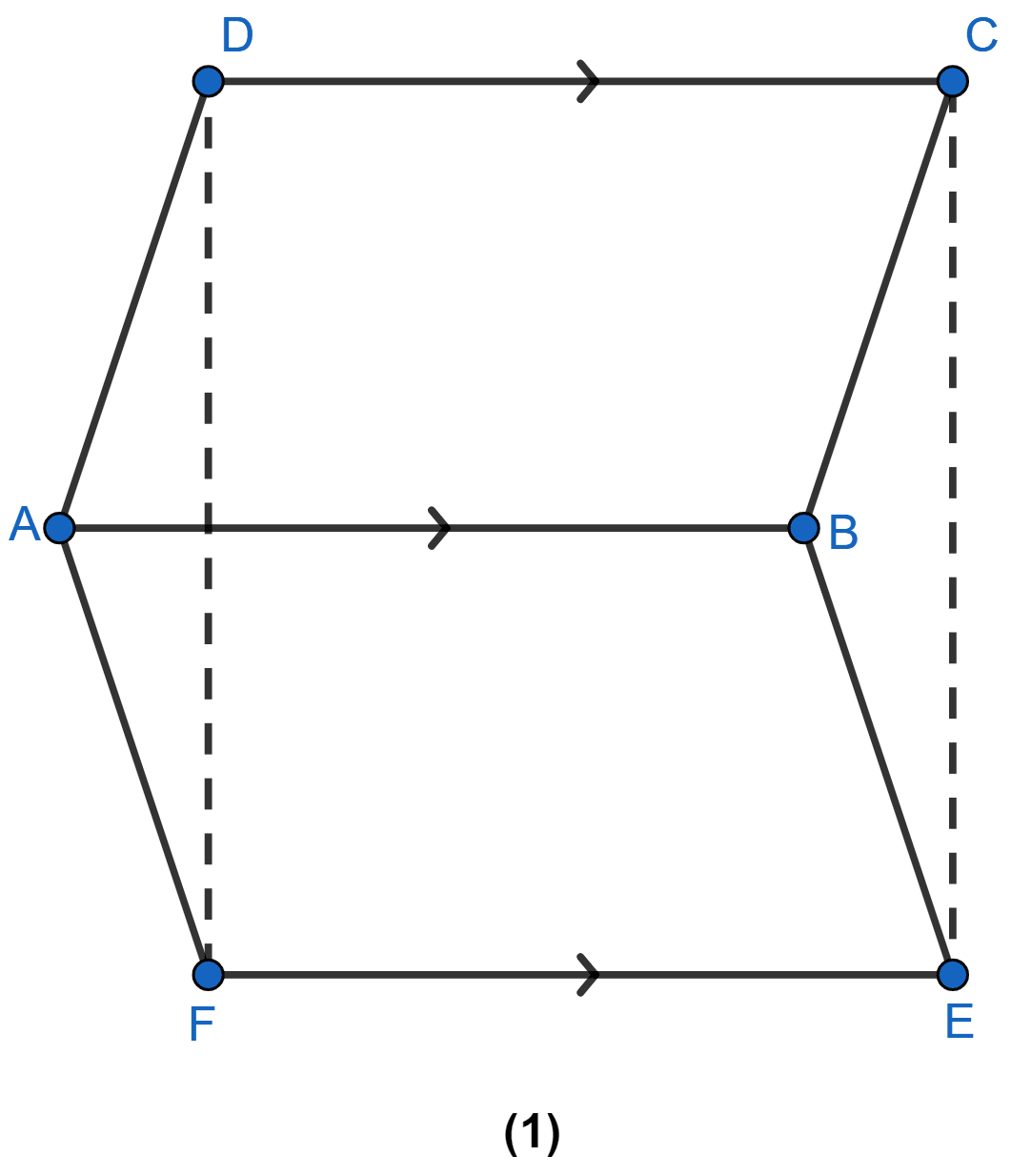
Answer

(i) DC || AB and DC = AB [∵ ABCD is a || gm] .......... (1)

FE || AB and FE = AB [∵ ABEF is a || gm] ...........(2)

∴ DC || FE and DC = FE [From (1) and (2)]

Hence, proved that CDFE is a || gm.

(ii) Since, CDEF is a || gm.

So, FD = EC (As opposite sides of a || gm are equal)

Hence, proved that FD = EC.

(iii) In ∆AFD and ∆BEC, we have

AD = BC [Opposite sides of || gm ABCD are equal]

AF = BE [Opposite sides of || gm ABEF are equal]

FD = CE [Opposite sides of || gm CDFE are equal]

Hence, ∆AFD ≅ ∆BEC by S.S.S axiom of congruency

Hence, proved that ∆AFD ≅ ∆BEC.

In the figure (2) given below, ABCD is a parallelogram, ADEF and AGHB are two squares. Prove that FG = AC.

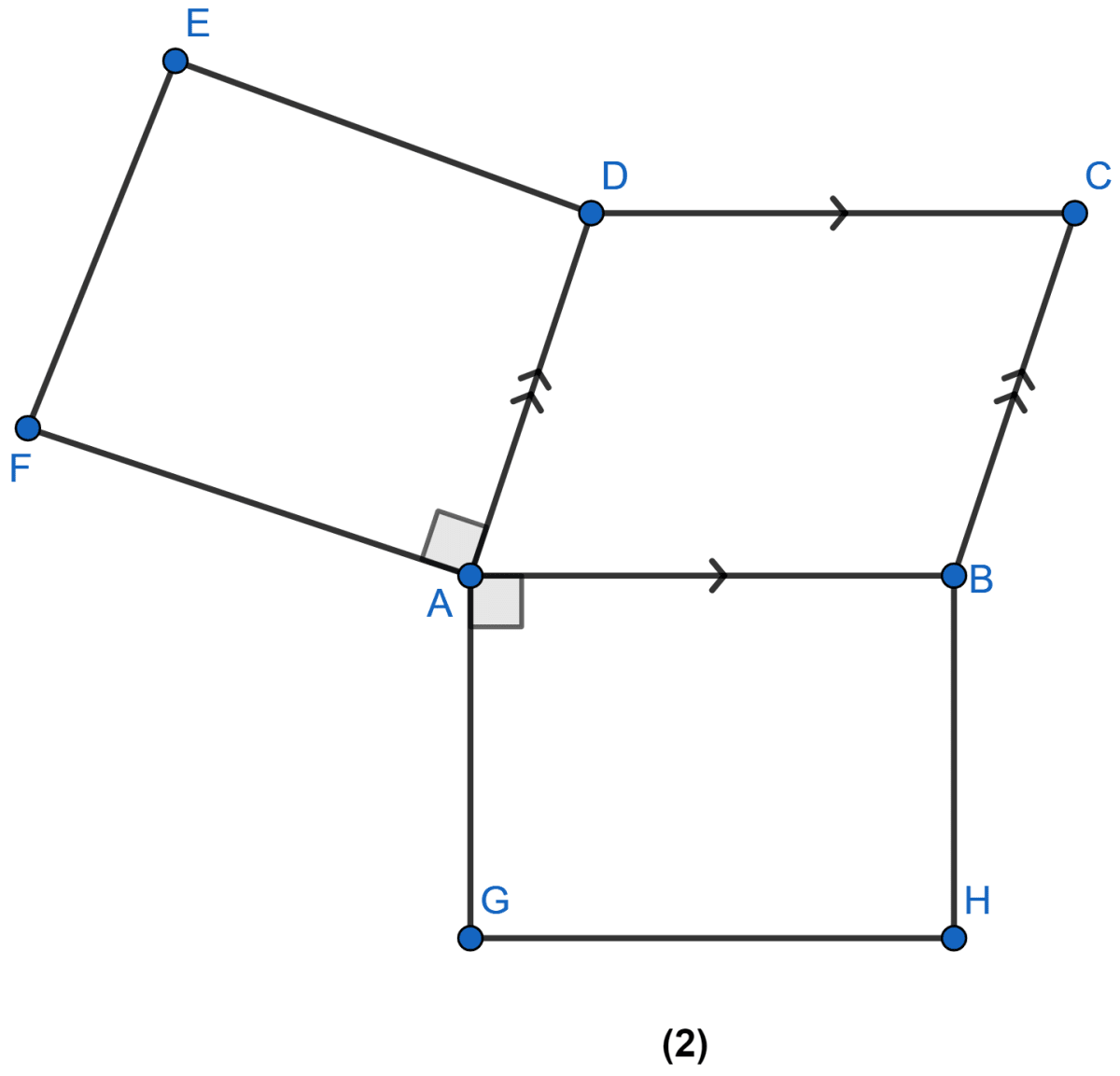
Answer

From figure,

⇒ ∠FAG + ∠GAB + ∠BAD + ∠FAD = 360° [∵ At a point total angle is 360°]

⇒ ∠FAG + 90° + 90° + ∠BAD = 360°

⇒ ∠FAG = 360 – 90° – 90° – ∠BAD

⇒ ∠FAG = 180° – ∠BAD .........(i)

⇒ ∠ABC + ∠BAD = 180° [Sum of Adjacent angle in || gm is equal to 180°]

⇒ ∠ABC = 180° – ∠BAD .........(ii)

⇒ ∠FAG = ∠ABC [From (i) and (ii)]

In || gm ABCD,

AB = CD and AD = BC.

Since, ADEF is a square,

so, AD = DE = EF = FA.

So, BC = FA.

In ∆AFG and ∆ABC, we have

⇒ AF = BC [Proved above]

⇒ AG = AB (∵ AGBH is a square)

⇒ ∠FAG = ∠ABC [Proved above]

So, ∆AFG ≅ ∆ABC by S.A.S axiom of congruency

∴ FG = AC. [By C.P.C.T]

Hence, proved that FG = AC.

ABCD is a rhombus in which ∠A = 60°. Find the ratio AC : BD.

Answer

Rhombus ABCD is shown in the figure below:

In △ABD,

⇒ AB = AD (Sides of rhombus are equal.)

⇒ ∠B = ∠D = x (let) (∵ angles opposite to equal sides are equal)

⇒ ∠A + ∠B + ∠D = 180°

⇒ 60° + x + x = 180°

⇒ 2x = 180° - 60°

⇒ 2x = 120°

⇒ x = 60°.

∴ ABD is an equilateral triangle.

So, BD = AB = AD = a (let)

Since, diagonals of rhombus bisect each other,

OB = $\dfrac{a}{2}$

In right angled triangle AOB,

AB² = AO² + OB²

a² = AO² + $\Big(\dfrac{a}{2}\Big)^2$

AO² = a² - $\dfrac{a^2}{4} = \dfrac{3a^2}{4}$

AO = $\dfrac{\sqrt{3}a}{2}$

AC = 2AO = $\sqrt{3}a$

AC : BD = $\sqrt{3}a : a = \sqrt{3} : 1$.

Hence, AC : BD = $\sqrt{3} : 1$.

Using ruler and compasses only, construct the quadrilateral ABCD in which ∠BAD = 45°, AD = AB = 6cm, BC = 3.6cm, CD = 5cm. Measure ∠BCD.

Answer

Steps of construction:

1. Draw a line segment AB = 6 cm
2. At A, construct ∠BAX = 45°.
3. From AX, cut off AD = 6 cm.
4. With B as centre and radius 3.6 cm, draw an arc.
5. With D as centre and radius 5 cm, draw an arc to meet the previous arc at C.
6. Join BC and DC. Then, ABCD is the required quadrilateral.

On measuring ∠BCD, it is 63°.

Hence, ∠BCD = 63°.

Draw a quadrilateral ABCD with AB = 6 cm, BC = 4 cm, CD = 4 cm and ∠ABC = ∠BCD = 90°.

Answer

Steps of construction:

1. Draw a line segment BC = 4 cm.
2. At B, construct ∠CBX = 90° and cut off BA = 6 cm.
3. At C, construct ∠BCY = 90° and cut off CD = 4 cm.
4. Join AD. Then, ABCD is the required quadrilateral.

Using ruler and compasses only, construct the quadrilateral ABCD given that AB = 5 cm, BC = 2.5 cm, CD = 6 cm, ∠BAD = 90° and the diagonal AC = 5.5 cm.

Answer

Steps of construction:

1. Draw a line segment AB = 5cm.
2. With centre A and radius 5.5 cm, draw an arc.
3. With centre B and radius 2.5 cm, draw an arc to meet the previous arc at C.
4. Join AC and BC.
5. At A, construct ∠BAX = 90°.
6. With centre C and radius 6 cm, draw an arc intersecting AX at D.
7. Join CD. Then, ABCD is the required quadrilateral.

Construct a quadrilateral ABCD in which AB = 3.3 cm, BC = 4.9 cm, CD = 5.8 cm, DA = 4 cm and BD = 5.3 cm.

Answer

Steps of construction:

1. Draw a line segment AB = 3.3 cm.
2. With centre A and radius 4 cm, draw an arc.
3. With centre B and radius 5.3 cm, draw an arc to meet the previous arc at D.
4. Join AD and BD.
5. With centre B and radius 4.9 cm, draw an arc.
6. With centre D and radius 5.8 cm, draw an arc to meet the previous arc at C.
7. Join BC and DC. Then ABCD is the required quadrilateral.

Construct a trapezium ABCD in which AD || BC, AB = CD = 3 cm, BC = 5.2 cm and AD = 4 cm.

Answer

Steps of construction:

1. Draw a line segment BC = 5.2 cm.
2. From BC, cut off BE = 4 cm.
3. With centre E and radius 3 cm, draw an arc.
4. With centre C and radius 3 cm, draw an arc to meet the previous arc at D.
5. Join ED and CD.
6. With centre D and radius 4 cm, draw an arc.
7. With centre B and radius 3 cm, draw an arc to meet the previous arc at A.
8. Join BA and DA. Then ABCD is the required quadrilateral.

Construct a trapezium ABCD in which AD || BC, ∠B = 60°, AB = 5 cm, BC = 6.2 cm and CD = 4.8 cm.

Answer

Steps of construction:

1. Draw a line segment BC = 6.2 cm.
2. At B, construct ∠CBX = 60°.
3. With centre B and radius 5 cm, draw an arc intersecting BX at A.
4. From A, draw a line AY parallel to BC.
5. With centre C and radius 4.8 cm, draw an arc which intersects AY at D.
6. Join CD. Then ABCD is the required trapezium.

Using ruler and compasses only, construct a parallelogram ABCD with AB = 5.1 cm, BC = 7 cm and ∠ABC = 75°.

Answer

Steps of construction:

1. Draw a line segment BC = 7 cm.
2. At B, construct ∠CBX = 75°.
3. With B as center and radius 5.1 cm, draw an arc intersecting BX at A.
4. With A as center and radius 7 cm, draw an arc.
5. With C as center and radius 5.1 cm, draw an arc to meet the previous arc at D.
6. Join AD and CD. Then ABCD is the required parallelogram.

Using ruler and compasses only, construct a parallelogram ABCD in which AB = 4.6 cm, BC = 3.2 cm and AC = 6.1 cm.

Answer

Steps of construction:

1. Draw a line segment AB = 4.6 cm
2. With A as center and radius 6.1 cm, draw an arc.
3. With B as center and radius 3.2 cm, draw an arc to meet the previous arc at C.
4. Join AC and BC.
5. Again, with A as center and radius 3.2 cm, draw an arc.
6. With C as center and radius 4.6 cm, draw an arc to meet the previous arc at D.
7. Join AD and CD. Then ABCD is the required parallelogram.

Using ruler and compasses, construct a parallelogram ABCD given that AB = 4 cm, AC = 10 cm, BD = 6 cm. Measure BC.

Answer

Steps of construction:

1. Draw a line segment AB = 4 cm.
2. Construct triangle OAB such that
   OA = $\dfrac{1}{2}$ x AC = 5cm
   OB = $\dfrac{1}{2}$ x BD = 3cm
   With A as center and radius 5 cm and with centre B and radius 3 cm, draw arcs intersecting each other at O.
   As, diagonals of || gm bisect each other.
3. Produce AO to C such that OA = OC = 5cm.
4. Produce BO to D such that OB = OD = 3cm.
5. Join AD, BC and CD. Then ABCD is the required parallelogram.

On measuring, BC = 7.2 cm.

Hence, BC = 7.2 cm.

Using ruler and compasses only, construct a parallelogram ABCD such that BC = 4 cm, diagonal AC = 8.6 cm and diagonal BD = 4.4 cm. Measure the side AB.

Answer

Steps of construction:

1. Draw a line segment BC = 4 cm.
2. Construct triangle OBC such that
   OB = $\dfrac{1}{2}$ x BD = 2.2 cm
   OC = $\dfrac{1}{2}$ x AC = 4.3 cm
3. With B as center and radius 2.2 cm and with centre C and radius 4.3 cm, draw arcs intersecting each other at O.
   Since, diagonals of || gm bisect each other.
4. Produce BO to D such that BO = OD = 2.2 cm.
5. Produce CO to A such that CO = OA = 4.3 cm.
6. Join AB, AD and CD. Then ABCD is the required parallelogram.

On measuring AB = 5.6 cm.

Hence, AB = 5.6 cm.

Use ruler and compasses to construct a parallelogram with diagonals 6 cm and 8 cm in length having given the acute angle between them is 60°. Measure one of the longer sides.

Answer

Steps of construction:

Let AC = 6 cm and BD = 8 cm.

1. Draw AO = $\dfrac{1}{2}AC = \dfrac{1}{2} \times 6 = 3\text{ cm and}$ produce AO to C such that OC = OA.
2. At O construct ∠COP = 60°.
3. From OP cut off OD = $\dfrac{1}{2} BD = \dfrac{1}{2} \times 8 = 4$ cm, produce DO to B such that OB = OD.
4. Join AB, BC, CD and DA. Then ABCD is the required parallelogram.

On measuring the length of longer side AD = BC = 6.1 cm.

Hence, length of longer side = 6.1 cm.

Using ruler and compasses only, draw a parallelogram whose diagonals are 4 cm and 6 cm long and contain an angle of 75°. Measure and write down the length of one of the shorter sides of the parallelogram.

Answer

Steps of construction:

Let AC = 4 cm and BD = 6 cm.

1. Draw AO = $\dfrac{1}{2}AC = \dfrac{1}{2} \times 4 = 2\text{ cm and}$ produce AO to C such that OC = OA.
2. At O construct ∠COP = 75°.
3. From OP cut off OD = $\dfrac{1}{2} BD = \dfrac{1}{2} \times 6 = 3$ cm, produce DO to B such that OB = OD.
4. Join AB, BC, CD and DA. Then ABCD is the required parallelogram.

On measuring shorter sides, we get

AB = CD = 3.1 cm.

Hence, length of shorter side = 3.1 cm.

Using ruler and compasses only, construct a parallelogram ABCD with AB = 6 cm, altitude = 3.5 cm and side BC = 4 cm. Measure the acute angles of the parallelogram.

Answer

Steps of construction:

1. Draw AB = 6 cm.
2. At B, draw BP ⊥ AB.
3. From BP, cut BE = 3.5 cm = height of || gm.
4. Through E draw QR parallel to AB.
5. With B as centre and radius = 4 cm draw an arc which cuts QR at C.
   Since, opposite sides of || gm are equal.
   So, AD = BC = 4 cm
6. With A as centre and radius = 4 cm draw an arc which cuts QR at D.
7. Join AD, BC and CD. Then ABCD is the required parallelogram.

On measuring the acute angle of parallelogram it is equal to 61°.

Hence, acute angle = 61°.

The perpendicular distances between the pairs of opposite sides of a parallelogram ABCD are 3 cm and 4 cm and one of its angles measures 60°. Using ruler and compasses only, construct ABCD.

Answer

Steps of construction:

1. Draw a straight-line PQ, take a point A on it.
2. At A, construct ∠QAF = 60°
3. At A, draw AE ⊥ PQ from AE cut off AN = 3 cm
4. Through N draw a straight line to PQ to meet AF at D.
5. At A, draw AG ⊥ AD, from AG cut off AM = 4 cm.
6. Through M, draw a straight line parallel to AD to meet AQ at B and ND at C.
7. Join AB, BC, CD and DA. Then, ABCD is the required parallelogram.

Using ruler and compasses, construct a rectangle ABCD with AB = 5 cm and AD = 3 cm.

Answer

Steps of construction:

1. Draw a straight-line AB = 5 cm.
2. At A and B construct ∠XAB = ∠YBA = 90°.
3. From XA and YB cut off AD and BC = 3 cm each.
4. Join CD. Then ABCD is the required rectangle.

Using ruler and compasses only, construct a rectangle each of whose diagonals measures 6 cm and the diagonals intersect at an angle of 45°.

Answer

Steps of construction:

1. Draw a line segment AC = 6 cm.
2. Bisect AC at O.
3. At O, draw a ray XY making an angle of 45° at O.
4. From XY, cut off OB = OD = $\dfrac{6}{2}$ = 3 cm each.
5. Join AB, BC CD and DA. Then ABCD is the required rectangle.

Using ruler and compasses only, construct a square having a diagonal of length 5 cm. Measure its sides correct to the nearest millimeter.

Answer

Steps of construction:

1. Draw a line segment AC = 5 cm.
2. Draw its perpendicular bisector XY bisecting it at O.
3. From XY, cut off OB = OD = $\dfrac{5}{2}$ = 2.5 cm.
4. Join AB, BC, CD and DA. Then ABCD is the required square.

On measuring, each side = 3.5 cm.

Hence, length of side of square = 3.5 cm.

Using ruler and compasses only construct a rhombus ABCD, given that AB = 5 cm, AC = 6 cm. Measure ∠BAD.

Answer

Steps of construction:

1. Draw a line segment AB = 5 cm.
2. With centre A and radius 6 cm, with centre B and radius 5cm, draw arcs intersecting each other at C.
3. Join AC and BC.
4. With centre A and C and radius 5cm, draw arcs intersecting each other at D.
5. Join AD and CD. Then ABCD is the required rhombus.

On measuring, ∠BAD = 106°.

Hence, ∠BAD = 106°.

Using ruler and compasses only, construct rhombus ABCD with sides of length 4 cm and diagonal AC of length 5 cm. Measure ∠ABC.

Answer

Steps of construction:

1. Draw a line segment AC = 5 cm.
2. With centre A and C and radius 4 cm, draw arcs intersecting each other above and below AC at D and B.
3. Join AB, BC, CD, DA and BD. The ABCD is the required rhombus.

On measuring, ∠ABC = 78°.

Hence, ∠ABC = 78°.

Construct a rhombus PQRS whose diagonals PR, QS are 8 cm and 6 cm respectively.

Answer

Steps of construction:

1. Draw a line segment PR = 8 cm.
2. Draw its perpendicular bisector XY intersecting it at O.
3. From XY, cut off OQ = OS = $\dfrac{6}{2}$ = 3 cm each.
4. Join PQ, QR, RS and SP. Then PQRS is the required rhombus.

Construct a rhombus ABCD of side 4.6 cm and ∠BCD = 135°, by using ruler and compasses only.

Answer

Steps of construction:

1. Draw a line segment BC = 4.6 cm.
2. At C, draw a ray CX making an angle of 135° and cut off CD = 4.6 cm.
3. With centres B and D, and radius 4.6 cm draw arcs intersecting each other at A.
4. Join BA and DA. Then ABCD is the required rhombus.

Construct a trapezium in which AB || CD, AB = 4.6 cm, ∠ABC = 90°, ∠DAB = 120° and the distance between parallel sides is 2.9 cm.

Answer

Steps of construction:

1. Draw a line segment AB = 4.6 cm.
2. At B, draw a ray BZ making an angle of 90° and cut off BC = 2.9 cm. (distance between AB and CD)
3. At C, draw a parallel line XY to AB.
4. At A, draw a ray making an angle of 120° meeting XY at D.
5. Join AD, DC. Then ABCD is the required trapezium.

Construct a trapezium ABCD when one of parallel sides AB = 4.8 cm, height = 2.6 cm, BC = 3.1 cm and AD = 3.6 cm.

Answer

Step construction:

1. Draw a line segment AB = 4.8 cm.
2. At A, draw a ray AZ making an angle of 90° and cut off AL = 2.6 cm.
3. At L, draw a ray LX parallel to AB.
4. With centre A and radius 3.6 cm and with centre B and radius 3.1 cm, draw arcs intersecting LX at D and C respectively.
5. Join AD and BC. Then ABCD is the required trapezium.

Construct a regular hexagon of side 2.5 cm.

Answer

Steps of construction:

1. With O as centre and radius = 2.5 cm, draw a circle
2. Take any point A on the circumference of circle.
3. With A as centre and radius = 2.5 cm, draw an arc which cuts the circumference of circle at B.
4. With B as centre and radius = 2.5 cm, draw an arc which cuts the circumference of circle at C.
5. With C as centre and radius = 2.5 cm, draw an arc which cuts the circumference of circle at D.
6. With D as centre and radius = 2.5 cm, draw an arc which cuts the circumference of circle at E.
7. With E as centre and radius = 2.5 cm, draw an arc which cuts the circumference of circle at F.
8. Join AB, BC, CD, DE, EF and FA. Then ABCDEF is the required hexagon.

Three angles of a quadrilateral are 75°, 90° and 75°. The fourth angle is

1. 90°

2. 95°

3. 105°

4. 120°

Answer

Sum of angles of quadrilateral = 360°

Let fourth angle be x then,

75° + 90° + 75° + x = 360°

x + 240° = 360°

x = 360° - 240°

x = 120°.

Hence, Option 4 is the correct option.

A quadrilateral ABCD is a trapezium if

1. AB = DC

2. AD = BC

3. ∠A + ∠C = 180°

4. ∠B + ∠C = 180°

Answer

In a trapezium the sum of co-interior adjacent angles = 180°.

From figure,

∠B and ∠C are adjacent angles.

∴ ∠B + ∠C = 180°

Hence, Option 4 is the correct option.

If PQRS is a parallelogram, then ∠Q - ∠S is equal to

1. 90°

2. 120°

3. 0°

4. 180°

Answer

The opposite angles are equal in a parallelogram.

From figure,

∠Q and ∠S are opposite angles.

∴ ∠Q - ∠S = 0°

Hence, Option 3 is the correct option.

A diagonal of a rectangle is inclined to one side of the rectangle at 25°. The acute angle between the diagonals is

1. 55°

2. 50°

3. 40°

4. 25°

Answer

From figure,

In △OBC,

OB = OC (Since diagonals bisect each other)

∠OCB = ∠OBC = 25°

⇒ ∠OBC + ∠OCB + ∠BOC = 180°

⇒ 25° + 25° + ∠BOC = 180°

⇒ ∠BOC = 130°.

Since, AC is a straight line,

⇒ ∠AOB + ∠BOC = 180°

⇒ ∠AOB = 180° - 130° = 50°.

Hence, Option 2 is the correct option.

ABCD is a rhombus such that ∠ACB = 40°. Then ∠ADB is

1. 40°

2. 45°

3. 50°

4. 60°

Answer

From figure,

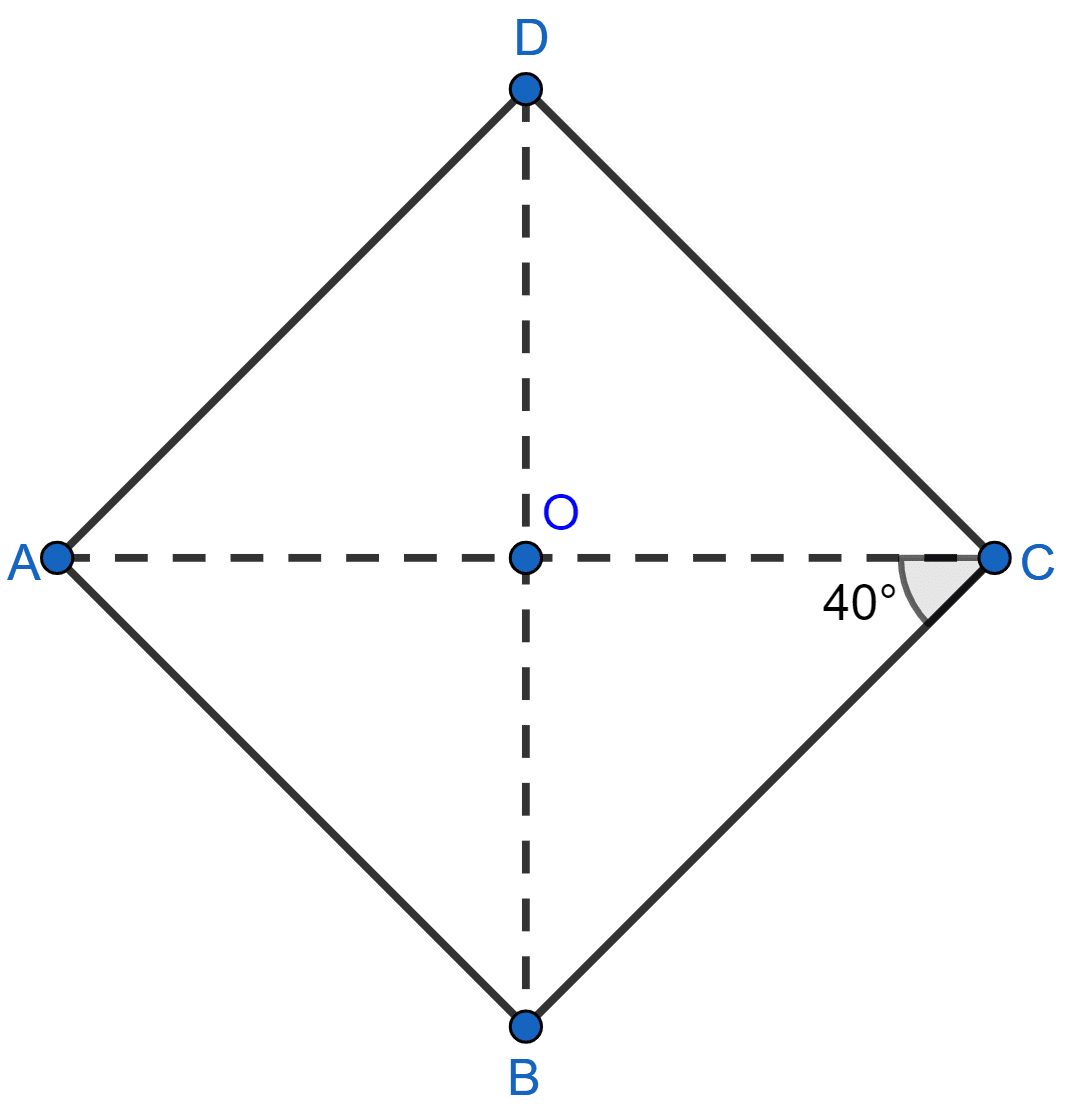
⇒ ∠DAO = ∠OCB = 40° (Alternate angles are equal.)

In △ADO,

⇒ ∠DAO + ∠AOD + ∠ODA = 180°

⇒ 40° + 90° + ∠ODA = 180°

⇒ ∠ODA = 180° - 130° = 50°.

From figure,

∠ADB = ∠ODA = 50°.

Hence, Option 3 is the correct option.

The diagonals AC and BD of a parallelogram ABCD intersect each other at the point O. If ∠DAC = 32° and ∠AOB = 70°, then ∠DBC is equal to

1. 24°

2. 86°

3. 38°

4. 32°

Answer

From figure,

∠ACB = ∠DAC = 32° (Alternate angles are equal)

AC is a straight line.

⇒ ∠AOB + ∠BOC = 180°

⇒ 70° + ∠BOC = 180°

⇒ ∠BOC = 180° - 70°

⇒ ∠BOC = 110°.

In △OBC,

⇒ ∠BOC + ∠OBC + ∠OCB = 180°

From figure,

⇒ ∠OCB = ∠ACB = 32°

⇒ 110° + ∠OBC + 32° = 180°

⇒ ∠OBC = 180° - 142° = 38°.

From figure,

∠DBC = ∠OBC = 38°.

Hence, Option 3 is the correct option.

If the diagonals of a square ABCD intersect each other at O, then △OAB is

1. an equilateral triangle

2. a right angled but not an isosceles triangle

3. an isosceles but not right angles triangle

4. an isosceles right angled triangle.

Answer

Since, diagonals of square bisect each other at 90°.

In △OAB,

AO = OB and ∠AOB = 90°.

Hence, it is an isosceles right angled triangle.

Hence, Option 4 is the correct option.

If the diagonals of a quadrilateral PQRS bisect each other, then the quadrilateral PQRS must be a

1. parallelogram

2. rhombus

3. rectangle

4. square

Answer

If the diagonals of a quadrilateral PQRS bisect each other, then the quadrilateral PQRS must be a parallelogram.

All the shapes rhombus, rectangle and square are parallelogram but not vice-versa.

Hence, they have all the properties of a parallelogram.

Hence, Option 1 is the correct option.

If the diagonals of a quadrilateral PQRS bisect each other at right angles, then the quadrilateral PQRS must be a

1. parallelogram

2. rectangle

3. rhombus

4. square

Answer

Diagonals of square and rhombus bisect each other at 90°.

Since, each square is a rhombus but not vice-versa.

Hence, if the diagonals of a quadrilateral PQRS bisect each other at right angles, then the quadrilateral PQRS must be a rhombus.

Hence, Option 3 is the correct option.

Which of the following statement is true for a parallelogram?

1. Its diagonals are equal.

2. Its diagonals are perpendicular to each other.

3. The diagonals divide the parallelogram into four congruent triangles.

4. The diagonals bisect each other.

Answer

Property of parallelogram is that its diagonal bisect each other.

Hence, Option 4 is the correct option.

Which of the following is not true for a parallelogram?

1. opposite sides are equal

2. opposite angles are equal

3. opposite angles are bisected by the diagonals

4. diagonals bisect each other

Answer

1, 2 and 4 are the properties of a parallelogram.

Hence, Option 3 is the correct option.

A quadrilateral in which the diagonals are equal and bisect each other at right angles is a

1. rectangle which is not a square

2. rhombus which is not a square

3. kite which is not a square

4. square

Answer

In square the diagonals are equal and bisect each other at right angles.

Hence, Option 4 is the correct option.

Consider the following two statements:

Statement 1: Sum of interior angles of any polygon in 360°.

Statement 2: Sum of interior angles of a rhombus in 360°.

Which of the following is valid?

1. Both the statements are true.

2. Both the statements are false.

3. Statement 1 is true, and Statement 2 is false.

4. Statement 1 is false, and Statement 2 is true.

Answer

The general formula for the sum of the interior angles of a polygon with n sides is (n - 2) x 180°.

For example:

For triangle (n = 3),

Sum of interior angles : (3 - 2) x 180° = 1 x 180° = 180°.

∴ Statement 1 is false.

For rhombus (n = 4),

Sum of interior angles : (4 - 2) x 180° = 2 x 180° = 360°.

∴ Statement 2 is true.

∴ Statement 1 is false, and Statement 2 is true.

Hence, option 4 is the correct option.

Assertion (A): All the interior angles of a square are right angles.

Reason (R): Diagonals of a square intersect at right angles.

1. Assertion (A) is true, Reason (R) is false.

2. Assertion (A) is false, Reason (R) is true.

3. Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).

4. Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).

Answer

By definition, a square is a quadrilateral with four equal sides and four right angles (each 90°).

∴ Assertion (A) is true.

In a square, the diagonals bisect each other at 90°.

∴ Reason (R) is true.

∴ Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).

Hence, option 4 is the correct option.

Assertion (A): If one angle of a rhombus is 70°, then its largest angle is 110°.

Reason (R): Every rhombus is a square.

1. Assertion (A) is true, Reason (R) is false.

2. Assertion (A) is false, Reason (R) is true.

3. Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).

4. Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).

Answer

A rhombus is a quadrilateral where all four sides are equal in length.

In a rhombus opposite angles are equal.

If one angle of the rhombus is 70°, then its opposite angle is also 70°.

In a rhombus consecutive angles are supplementary (sum to 180°).

Consecutive angle = 180° − 70° = 110°.

The four angles of the rhombus would be 70°, 110°, 70° and 110°.

The largest angle among these is 110°.

∴ Assertion (A) is true.

A rhombus is a quadrilateral in which all four sides equal. Its angles are not necessarily 90°.

A square is a special type of rhombus where all four angles are also right angles (90°).

Therefore, while every square is a rhombus, not every rhombus is a square.

∴ Reason (R) is false.

∴ Assertion (A) is true, Reason (R) is false.

Hence, option 1 is the correct option.

Assertion (A): Diagonals of adjoining quadrilateral bisect each other. Then ∠B = 135°.

Reason (R): If diagonals of a quadrilateral bisect each other, then it is a parallelogram.

1. Assertion (A) is true, Reason (R) is false.

2. Assertion (A) is false, Reason (R) is true.

3. Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).

4. Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).

Answer

We know that,

In a parallelogram, diagonals bisect each other.

∴ Reason (R) is true.

Given,

Diagonals of quadrilateral ABCD bisect each other. Thus, ABCD is a parallelogram.

In a parallelogram, the sum of any two adjacent angles is always 180 degrees (supplementary).

⇒ ∠A + ∠B = 180°

⇒ 45° + ∠B = 180°

⇒ ∠B = 180° − 45° = 135°.

∴ Assertion (A) is true.

∴ Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).

Hence, option 3 is the correct option.

In the adjoining figure, ABCD is a parallelogram. CB is produced to E such that BE = BC. Prove that AEBD is a parallelogram.

Answer

In ∆AEB and ∆BDC

EB = BC [Given]

∠ABE = ∠DCB [Corresponding angles]

AB = DC [Opposite sides of || gm ABCD are equal]

Thus, ∆AEB ≅ ∆BDC by S.A.S axiom

So, by C.P.C.T

BD = AE

In || gm ABCD,

BC = AD (As opposite sides of || gm are equal)

Given,

BC = BE

∴ AD = BE.

Since, opposite sides of quadrilateral AEBD are equal (i.e., BD = AE and AD = BE)

Hence, proved that AEBD is a parallelogram.

In the adjoining figure, ABC is an isosceles triangle in which AB = AC. AD bisects exterior angle PAC and CD || BA. Show that

(i) ∠DAC = ∠BCA

(ii) ABCD is a parallelogram.

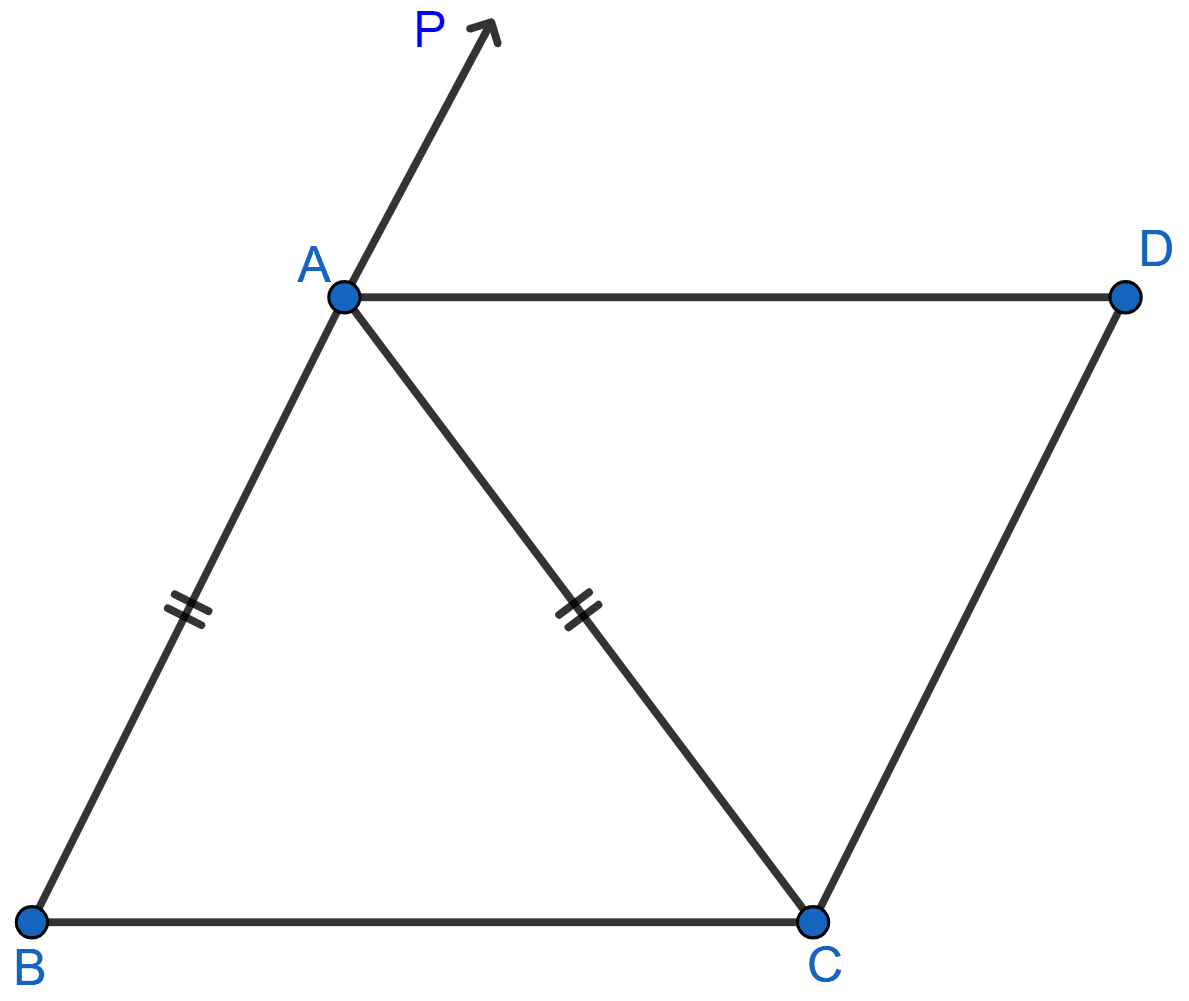
Answer

(i) In ∆ABC

AB = AC [Given]

∠C = ∠B [Angles opposite to equal sides are equal]

Since, ext. ∠PAC = ∠B + ∠C (Exterior angle is equal to the sum of opposite interior angles)

= ∠C + ∠C

= 2∠C

= 2∠BCA

Since AD bisects ext. ∠PAC, ∠PAC = 2∠DAC

⇒ 2∠DAC = 2∠BCA

⇒ ∠DAC = ∠BCA

Hence, proved that ∠DAC = ∠BCA.

(ii) Since, ∠DAC and ∠BCA are alternate angles and AC is transversal.

It proves that AD || BC.

Since, AD || BC and CD || BA.

Hence, proved that ABCD is a || gm.

Prove that the quadrilateral obtained by joining the mid-points of an isosceles trapezium is a rhombus.

Answer

P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively.

Join AC and BD.

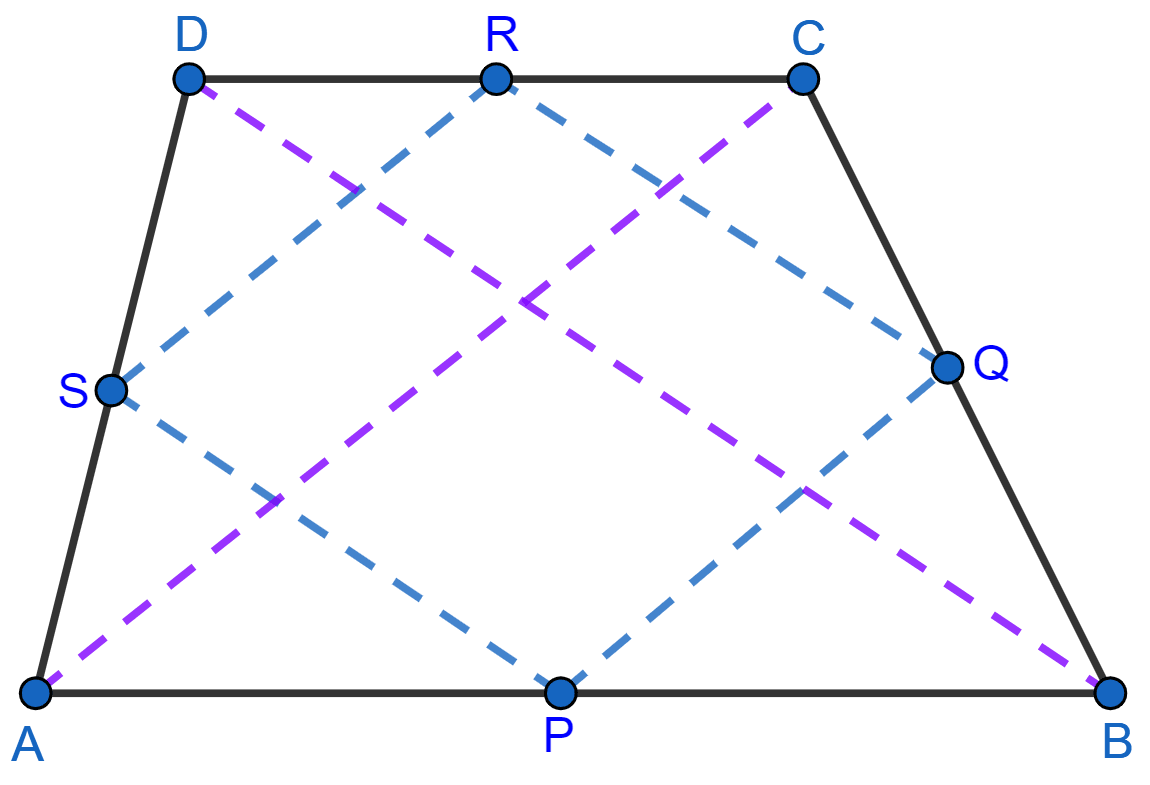
Since, ABCD is an isosceles trapezium

Its diagonals are equal.

AC = BD = x (let)

Now, in ∆ABC

P and Q are the mid-points of AB and BC

So, PQ || AC and PQ = $\dfrac{1}{2}$AC = $\dfrac{1}{2}$x (By midpoint theorem) … (i)

Similarly, in ∆ADC

S and R mid-point of AD and CD

So, SR || AC and SR = $\dfrac{1}{2}$AC = $\dfrac{1}{2}$x (By midpoint theorem) … (ii)

From (i) and (ii), we have

PQ || SR and PQ = SR = $\dfrac{1}{2}x$ .......(iii)

In ∆CBD,

R and Q are the mid-points of CD and BC

So, QR || BD and QR = $\dfrac{1}{2}$BD = $\dfrac{1}{2}$x (By midpoint theorem) … (iv)

Similarly, in ∆ABD

S and P mid-point of AD and AB

So, SP || BD and SP = $\dfrac{1}{2}$BD = $\dfrac{1}{2}$x (By midpoint theorem) … (v)

From (iv) and (v), we have

QR || SP and QR = SP = $\dfrac{1}{2}x$ .......(vi)

From (iii) and (vi) we get,

PQ = QR = SR = SP and QR || SP, PQ || SR.

So, sides of PQRS are equal and opposite sides are parallel.

Hence, proved that PQRS is a rhombus.

Find the size of each lettered angle in the following figure.

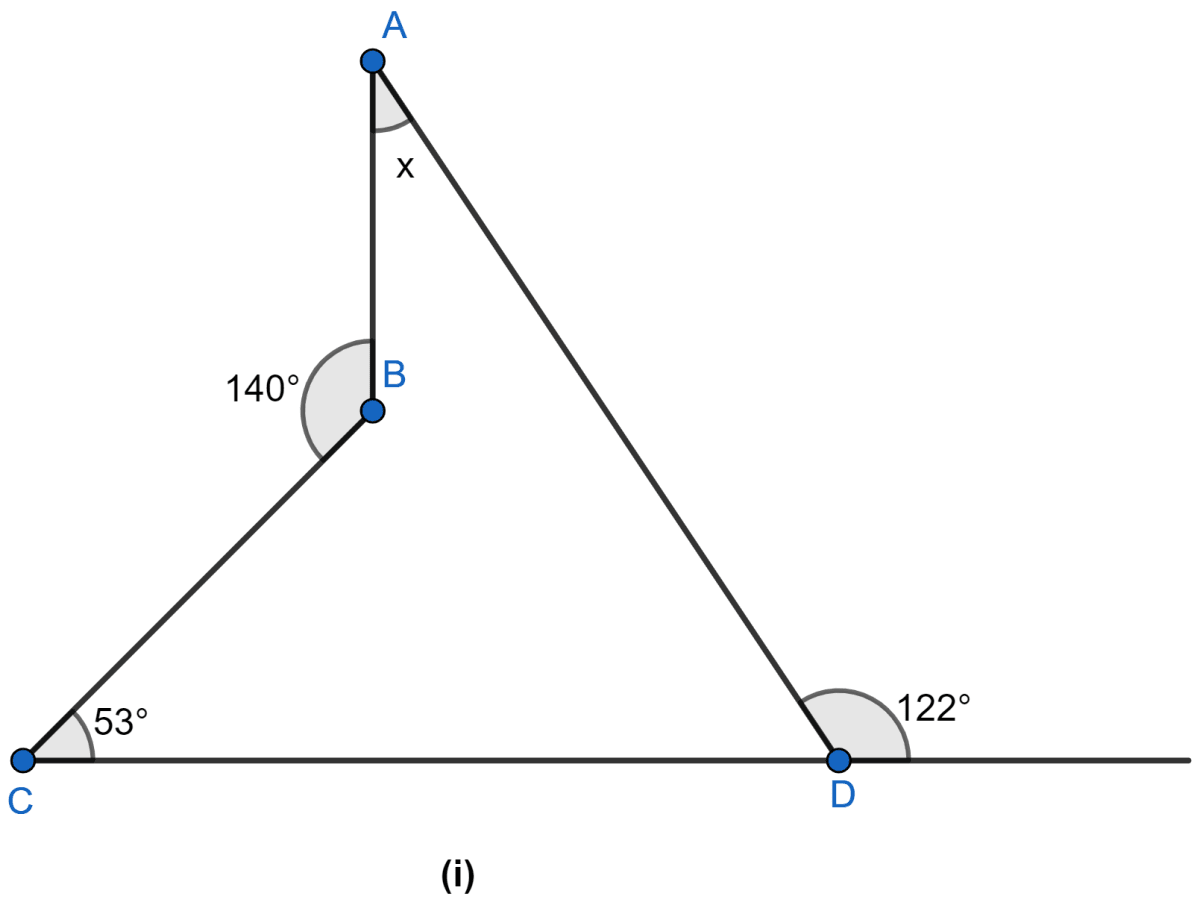
Answer

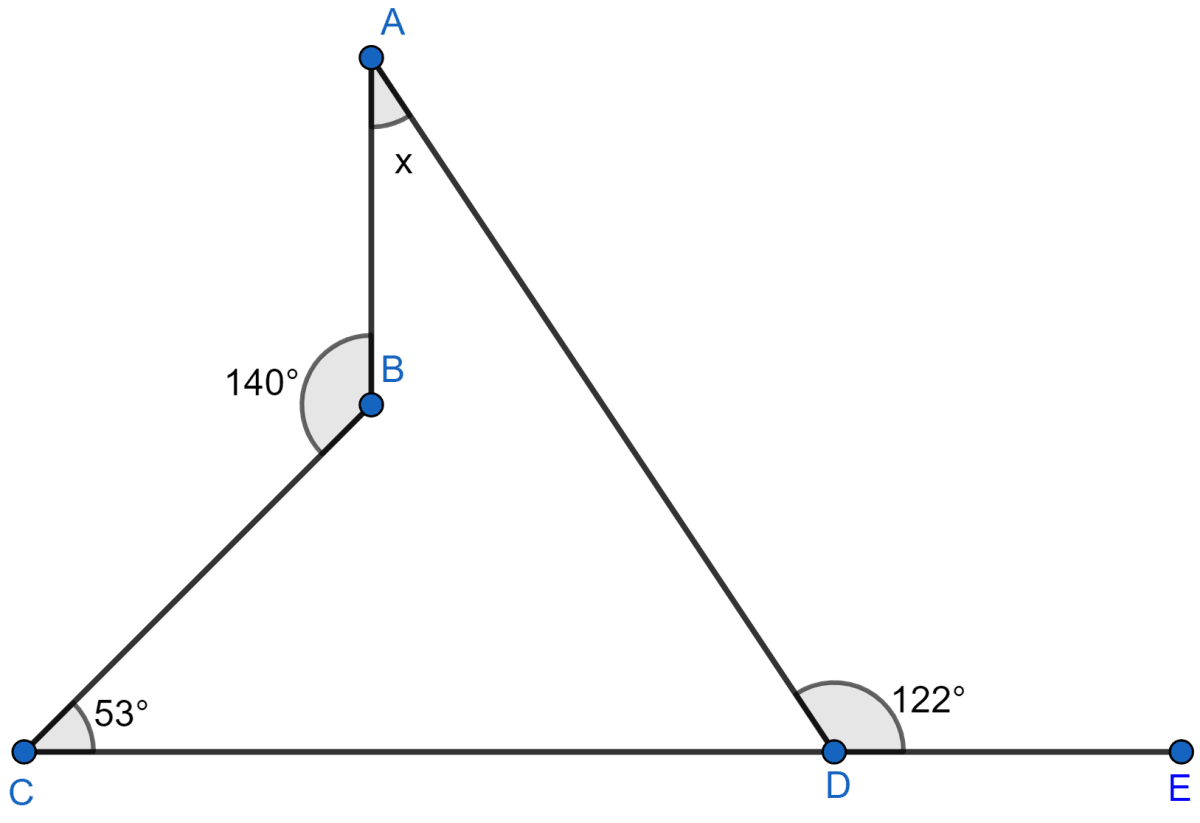
As CDE is a straight line

∠ADE + ∠ADC = 180°

122° + ∠ADC = 180°

∠ADC = 180° – 122° = 58° … (i)

Internal ∠ABC = 360° – 140° = 220° … (ii)

Now, in quadrilateral ABCD we have

⇒ ∠ADC + ∠BCD + ∠BAD + ∠ABC = 360° (As sum of all angles in a quadrilateral is 360°.)

⇒ 58° + 53° + x + 220° = 360° [Using (i) and (ii)]

⇒ 331° + x = 360°

⇒ x = 360° – 331°

⇒ x = 29°

Hence, x = 29°

Find the size of each lettered angle in the following figure.

Answer

As CD || BA [Given]

We can write ED || BA

⇒ ∠ECB = ∠CBA [Alternate angles are equal]

⇒ ∠CBA = 75°

Since, ABCD is a parallelogram, we have

⇒ ∠DAB + ∠CBA = 180° (AD || BC, sum of co-int ∠s = 180°)

⇒ (x + 66°) + 75° = 180°

⇒ x + 141° = 180°

⇒ x = 180° – 141°

⇒ x = 39° … (i)

Now, in ∆AMB

⇒ x + 30° + ∠AMB = 180° [Angles sum property of a triangle]

39° + 30° + ∠AMB = 180° [From (i)]

69° + ∠AMB + 180°

∠AMB = 180° – 69° = 111°

Since, ∠AMB = y [Vertically opposite angles are equal]

⇒ y = 111°

Hence, x = 39° and y = 111°

Find the size of each lettered angle in the following figure.

Answer

In △ADC,

AD = CD (Given)

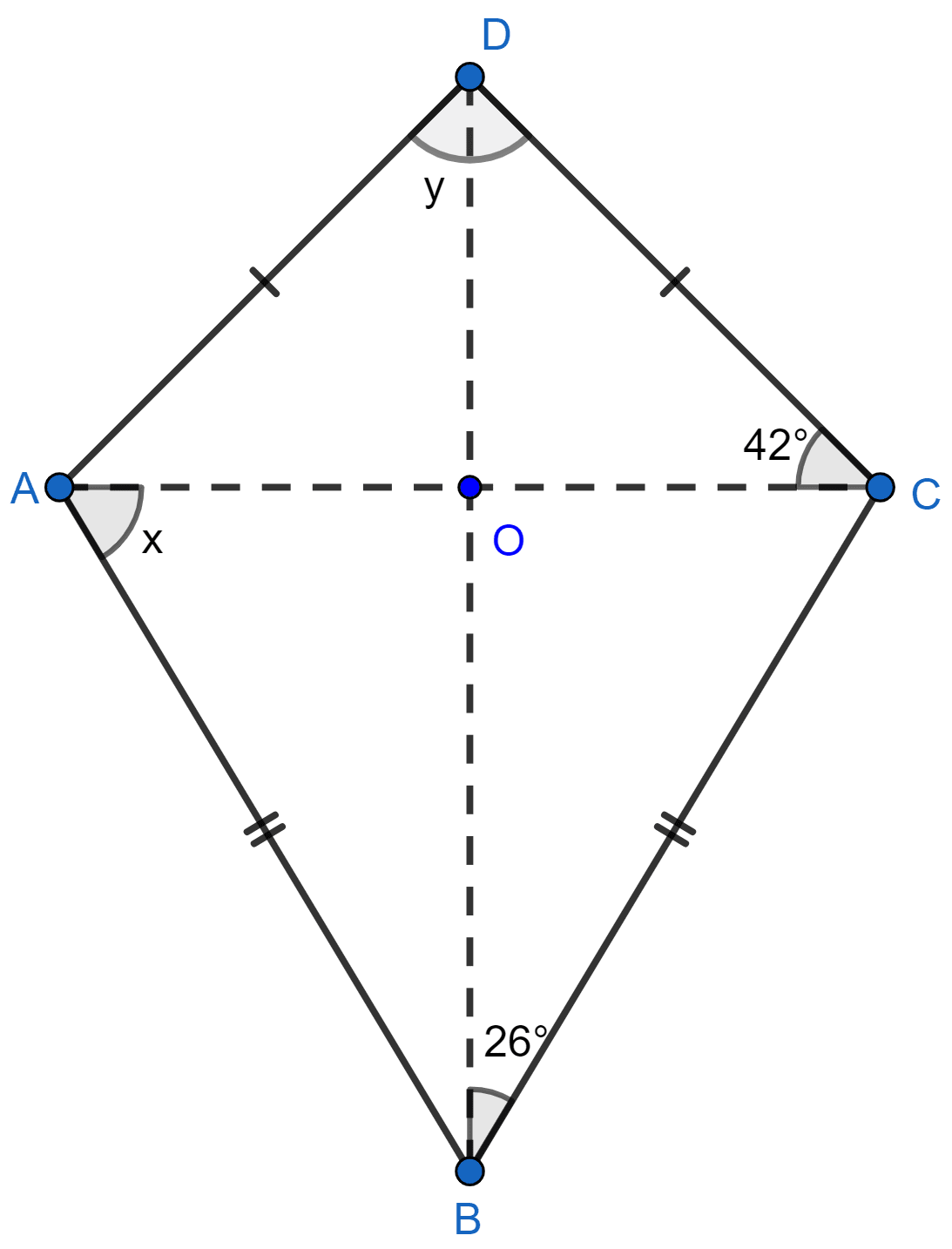
∠DAC = ∠DCA = 42° (Opposite angles of equal sides are equal).

⇒ ∠DAC + ∠DCA + ∠ADC = 180°

⇒ 42° + 42° + y = 180°

⇒ y + 84° = 180°

⇒ y = 96°

In △AOB and △COB,

AO = OC (Diagonals bisect each other)

AB = BC (Given)

∠AOB = ∠COB = 90° (Diagonals are perpendicular to each other)

Hence, △AOB ≅ △COB by RHS congruence rule.

By C.P.C.T. we get,

⇒ ∠ABO = ∠CBO = 26°

In △AOB,

⇒ ∠AOB + ∠ABO + ∠OAB = 180° (Sum of angles of triangle = 180°)

⇒ 90° + 26° + x = 180°

⇒ 116° + x = 180°

⇒ x = 180° - 116° = 64°

Hence, x = 64° and y = 96°.

Find the size of each lettered angle in the following figure:

Answer

Here, AB || CD and BC || AD

So, ABCD is a || gm

y = ∠ABC (As opposite angles of || gm are equal)

y = 2∠ABD (As diagonals bisect vertex angle so BD bisects ∠ABC)

y = 2 x 53° = 106°

Also, y + ∠DAB = 180° (DC || AB, sum of co-int ∠s = 180°)

∠DAB = 180° – 106° = 74°.

Thus, x = $\dfrac{1}{2}$∠DAB [As AC bisects ∠DAB]

⇒ x = $\dfrac{1}{2}$ x 74° = 37°

and ∠DAC = x = 37°

Also, z = ∠DAC = 37° [Alternate angles are equal]

Hence, x = 37°, y = 106° and z = 37°.

Find the size of each lettered angle in the following figure:

Answer

As ED is a straight line, we have

⇒ 60° + ∠AED = 180° [Linear pair]

⇒ ∠AED = 180° - 60° = 120°

Also, as CD is a straight line

⇒ 50° + ∠BCD = 180° [Linear pair]

⇒ ∠BCD = 180° – 50°

⇒ ∠BCD = 130°

In pentagon ABCDE, we have

⇒ ∠A + ∠B + ∠AED + ∠BCD + x = 540° [Sum of interior angles of pentagon is 540°]

⇒ 90° + 90° + 120° + 130° + x = 540°

⇒ 430° + x = 540°

⇒ x = 540° - 430°

⇒ x = 110°

Hence, value of x = 110°.

Find the size of each lettered angle in the following figure:

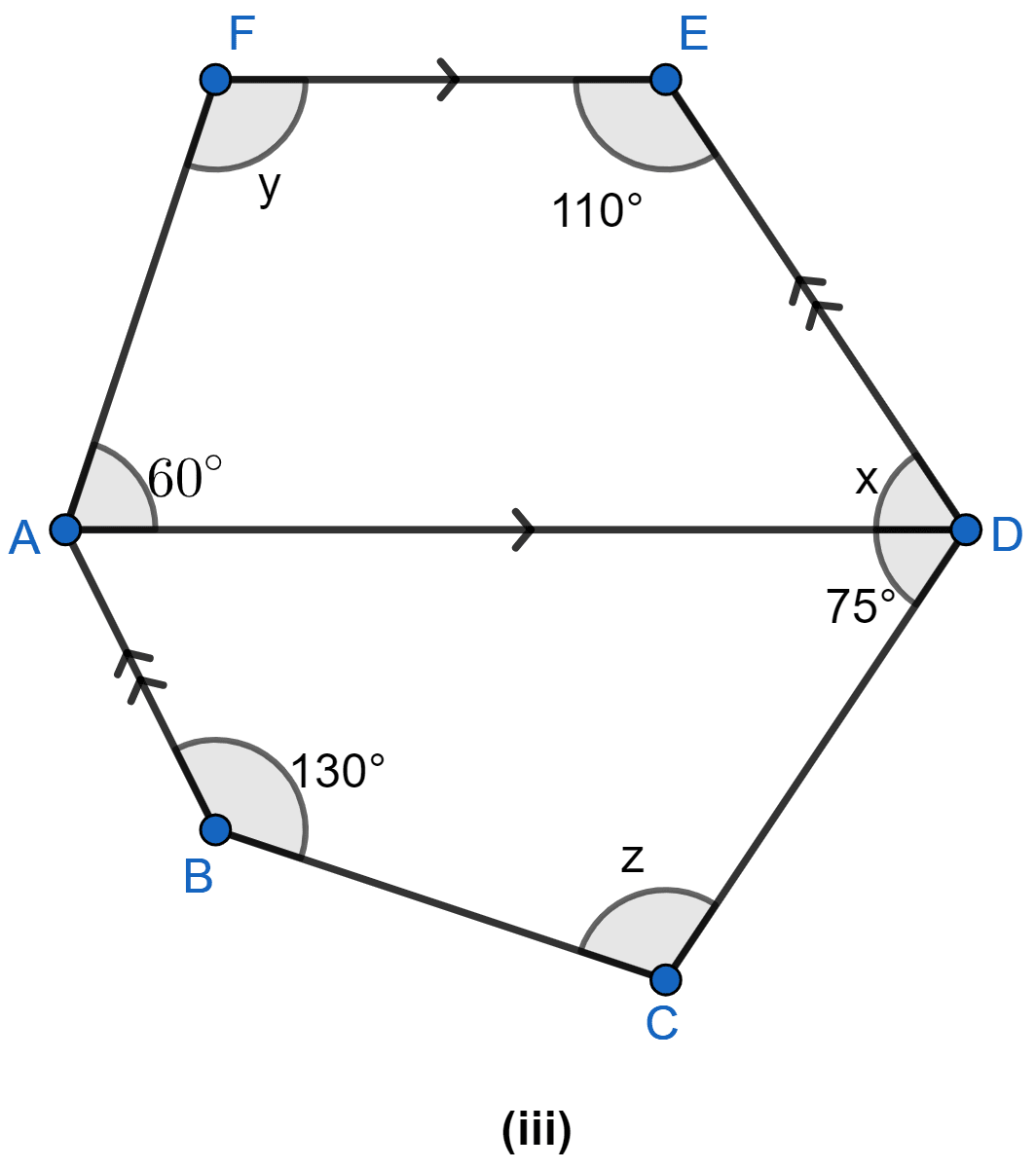
Answer

In given figure, AD || FE [Given]

⇒ 60° + y = 180° and x + 110° = 180° (∵ Sum of adjacent interior angle in trapezium = 180°)

⇒ y = 180° – 60° and x = 180° – 110°

⇒ y = 120° and x = 70°

Since, AB || DE [Given]

∠BAD = ∠ADE = 70° (Alternate angles are equal)

In quadrilateral ABCD,

⇒ ∠BAD + 75° + z + 130° = 360° (∵ Sum of angles of a quadrilateral = 360°)

⇒ 70° + 75° + z + 130° = 360°

⇒ 275° + z = 360°

⇒ z = 360° – 275° = 85°.

Hence, x = 70°, y = 120° and z = 85°.

In the adjoining figure, ABCD is a rhombus and DCFE is a square. If ∠ABC = 56°, find

(i) ∠DAG

(ii) ∠FEG

(iii) ∠GAC

(iv) ∠AGC.

Answer

(i) We know that,

Each angle of a square = 90°.

As ABCD is a rhombus so, AB = BC = DC = AD .......(i)

Also, CD = ED = FC = EF (As CDEF is a square) … (ii)

From (i) and (ii), we have

AB = BC = DC = AD = EF = FC = ED … (iii)

∠ABC = 56° [Given]

⇒ ∠ADC = ∠ABC = 56° [Opposite angle in rhombus are equal]

From figure,

⇒ ∠EDA = ∠EDC + ∠ADC = 90° + 56° = 146°

In ∆ADE,

⇒ DE = AD [From (iii)]

⇒ ∠DEA = ∠DAE [Equal sides have equal opposite angles]

From figure,

⇒ ∠DEA = ∠DAE = ∠DAG

⇒ ∠DAE + ∠DEA + ∠EDA = 180°

⇒ ∠DAG + ∠DAG + ∠EDA = 180°

⇒ 2∠DAG + 146° = 180°

⇒ 2∠DAG = 180° - 146° = 34°

⇒ ∠DAG = $\dfrac{34°}{2} = 17°$

⇒ ∠DAG = 17°.

Hence, ∠DAG = 17°.

(ii) Also,

⇒ ∠DEG = 17°

⇒ ∠FEG = ∠E – ∠DEG

= 90° – 17°

= 73°

Hence, ∠FEG = 73°.

(iii) In rhombus ABCD,

⇒ ∠A + ∠B = 180° (As AD || BC, the sum of co-interior angles = 180°.)

⇒ ∠A = 180° - ∠B = 180° - 56° = 124°

⇒ ∠DAC = $\dfrac{124°}{2} = 62°$ [∵ Diagonal AC bisects ∠A]

⇒ ∠DAC = 62°

⇒ ∠GAC = ∠DAC – ∠DAG

= 62° – 17° = 45°.

Hence, ∠GAC = 45°.

(iv) In ∆EDG,

⇒ ∠D + ∠DEG + ∠DGE = 180° [Angles sum property of a triangle]

⇒ 90° + 17° + ∠DGE = 180°

⇒ ∠DGE = 180° – 107° = 73°

Thus, ∠AGC = ∠DGE [Vertically opposite angles are equal]

⇒ ∠AGC = 73°.

Hence, ∠AGC = 73°.

If one angle of a rhombus is 60° and the length of a side is 8 cm, find the lengths of its diagonals.

Answer

Each side of rhombus ABCD is 8 cm.

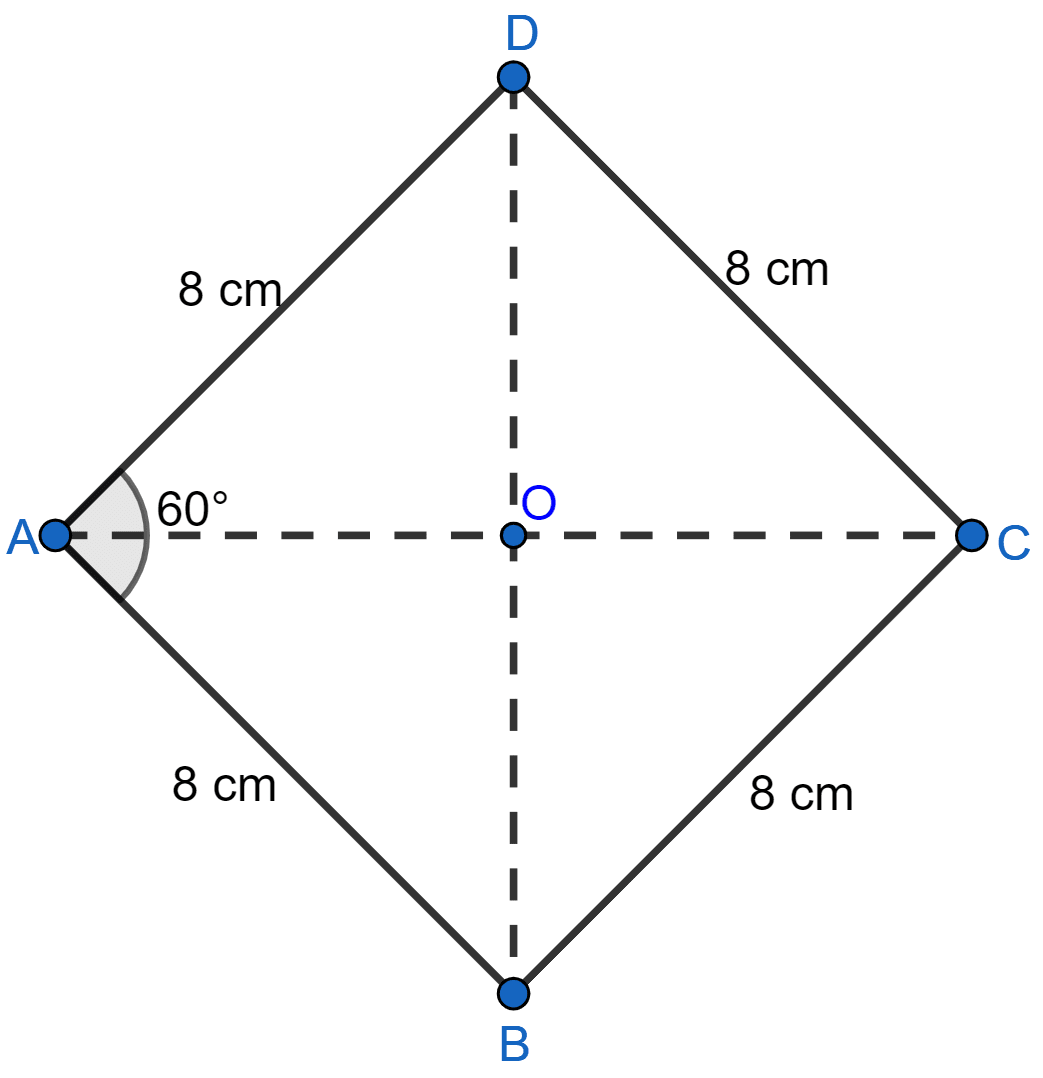
So, AB = BC = CD = DA = 8 cm.

Let ∠A = 60°.

In ∆ABD,

AB = AD

∠ADB = ∠ABD = x (let) (Angles opposite to equal sides are equal.)

⇒ ∠ADB + ∠ABD + ∠DAB = 180°

⇒ x + x + 60° = 180°

⇒ 2x + 60° = 180°

⇒ 2x = 180° - 60°

⇒ 2x = 120°

⇒ x = $\dfrac{120°}{2}$

⇒ x = 60°.

Since, all angles = 60°. Hence, △ABD is an equilateral triangle.

So, BD = 8 cm.

As we know, the diagonals of a rhombus bisect each other at right angles

AO = OC, BO = OD = 4cm and ∠AOB = 90°

Now, in right ∆AOB

By Pythagoras theorem,

⇒ AB² = AO² + OB²

⇒ 8² = AO² + 4²

⇒ 64 = AO² + 16

⇒ AO² = 64 – 16 = 48

⇒ AO = $\sqrt{48} = 4\sqrt{3}$ cm.

But, AC = 2AO

⇒ AC = $2 × 4\sqrt{3} = 8\sqrt{3}$ cm.

Hence, length of diagonals = 8 cm and $8\sqrt{3}$ cm.

Using ruler and compasses only, construct a parallelogram ABCD with AB = 5 cm, AD = 2.5 cm and ∠BAD = 45°. If the bisector of ∠BAD meets DC at E, prove that ∠AEB is a right angle.

Answer

Steps of construction:

1. Draw AB = 5.0 cm.
2. At A, construct ∠BAP = 45°.
3. With A as centre and radius 2.5 cm cut the line AP at D.
4. With D as centre and radius 5.0 cm, draw an arc.
5. With B as center and radius 2.5 cm, draw an arc to meet the previous arc at C.
6. Join BC and CD. Then, ABCD is the required parallelogram

Draw the bisector of ∠BAD, which cuts DC at E and join EB.

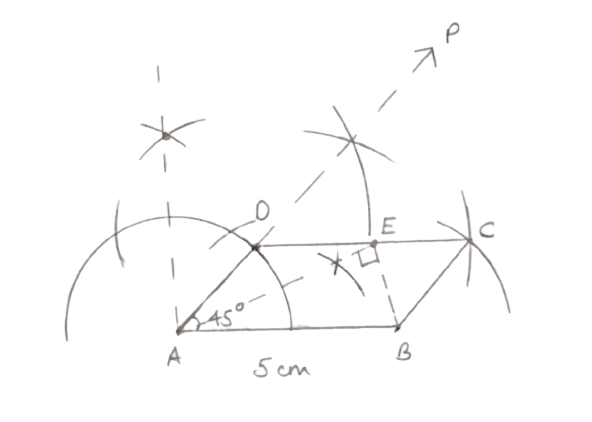
On measuring ∠AEB, it is equal to 90°.

Hence, proved that ∠AEB is a right angle.