Mid-point Theorem

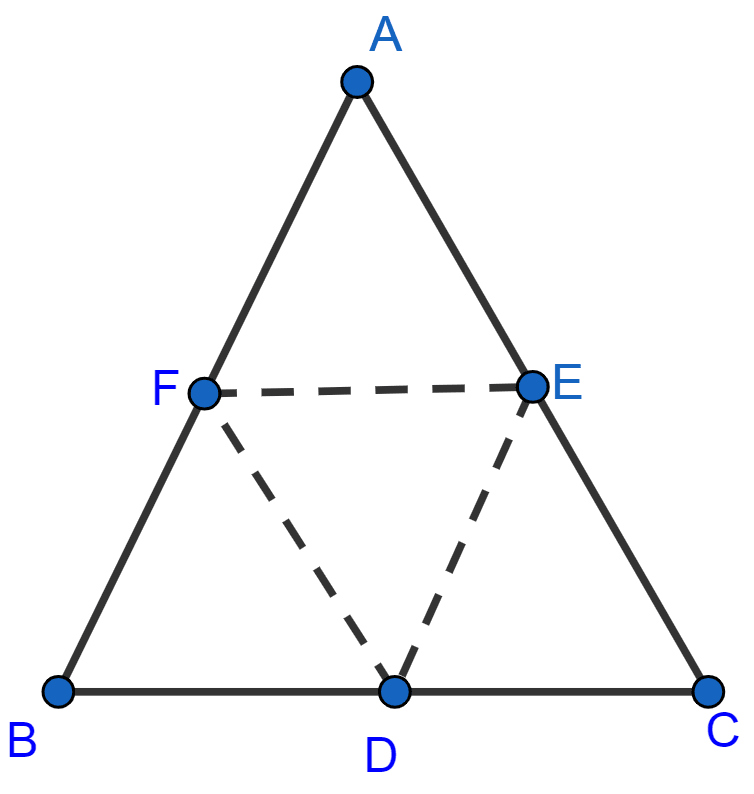
In the figure given below, D, E and F are mid-points of the sides BC, CA and AB respectively of △ ABC. If AB = 6 cm, BC = 4.8 cm and CA = 5.6 cm, find the perimeter of

(i) the trapezium of FBCE

(ii) the triangle DEF.

Answer

(i) Since F is midpoint of AB and E is midpoint of AC,

∴ FE is parallel to BC and FE = $\dfrac{1}{2}$BC = $\dfrac{1}{2}(4.8)$ = 2.4 cm (By midpoint theorem)

FB = $\dfrac{1}{2}$AB = $\dfrac{1}{2}(6)$ = 3 cm

EC = $\dfrac{1}{2}$AC = $\dfrac{1}{2}(5.6)$ = 2.8 cm.

Perimeter of trapezium FBCE = FE + EC + BC + FB = 2.4 + 2.8 + 4.8 + 3 = 13 cm.

Hence, perimeter of trapezium FBCE = 13 cm.

(ii) Since F is midpoint of AB and E is midpoint of AC,

∴ FE is parallel to BC and FE = $\dfrac{1}{2}$BC = $\dfrac{1}{2}(4.8)$ = 2.4 cm (By midpoint theorem)

Since F is midpoint of AB and D is midpoint of BC,

∴ FD is parallel to AC and FD = $\dfrac{1}{2}$AC = $\dfrac{1}{2}(5.6)$ = 2.8 cm (By midpoint theorem)

Since E is midpoint of AC and D is midpoint of BC,

∴ ED is parallel to AB and ED = $\dfrac{1}{2}$AB = $\dfrac{1}{2}(6)$ = 3 cm (By midpoint theorem)

Perimeter of △DEF = FE + FD + ED = 2.4 + 2.8 + 3 = 8.2 cm

Hence, perimeter of △DEF = 8.2 cm.

In the figure given below, D and E are mid-points of the sides AB and AC respectively. If BC = 5.6 cm and ∠B = 72°, compute

(i) DE

(ii) ∠ADE

Answer

(i) Since, D and E are mid-points of the sides AB and AC respectively,

∴ DE is parallel to BC and DE = $\dfrac{1}{2}BC = \dfrac{1}{2}(5.6)$ = 2.8 cm. (By midpoint theorem)

Hence, DE = 2.8 cm.

(ii) Since, DE is parallel to BC.

∴ ∠ABC = ∠ADE (Corresponding angles)

⇒ ∠ADE = 72°.

Hence, ∠ADE = 72°.

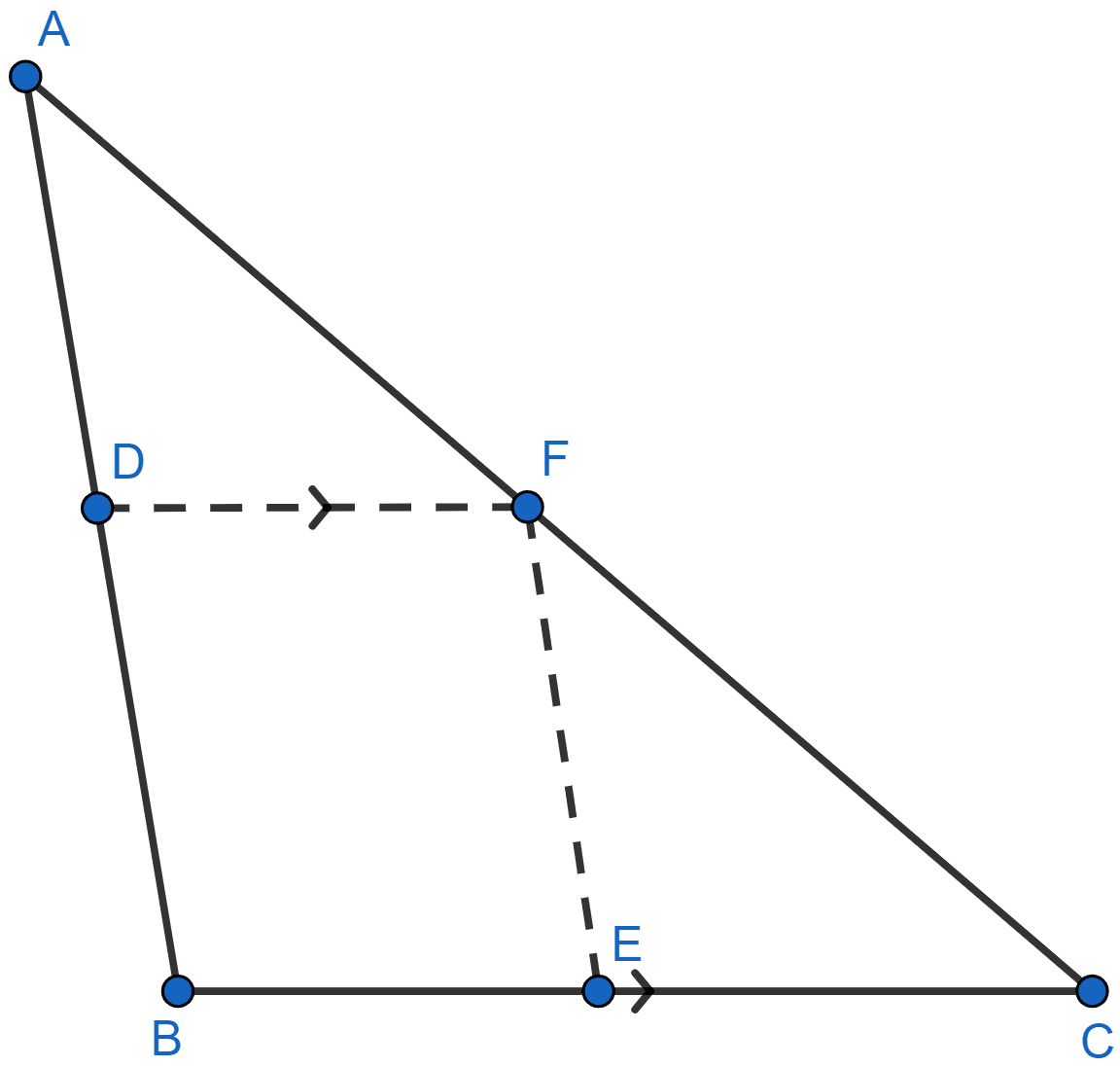
In the figure given below, D and E are mid-points of AB, BC respectively and DF || BC. Prove that DBEF is a parallelogram. Calculate AC if AF = 2.6 cm.

Answer

In △ABC,

D is the midpoint of AB and DF || BC

∴ F is the midpoint of AC (By converse of mid-point theorem)

F and E are midpoints of AC and BC respectively

∴ EF || AB ⇒ EF || DB .....(1)

From figure,

⇒ DF || BE ......(2)

Using 1 and 2,

⇒ EF || DB and DF || BE

Hence, proved that DBEF is a parallelogram.

F is the midpoint of AC we get,

AC = 2 × AF = 2 × 2.6 = 5.2 cm

Hence, AC = 5.2 cm

Prove that four triangles formed by joining in pairs, the mid-points of the sides of a triangle are congruent to each other.

Answer

From figure,

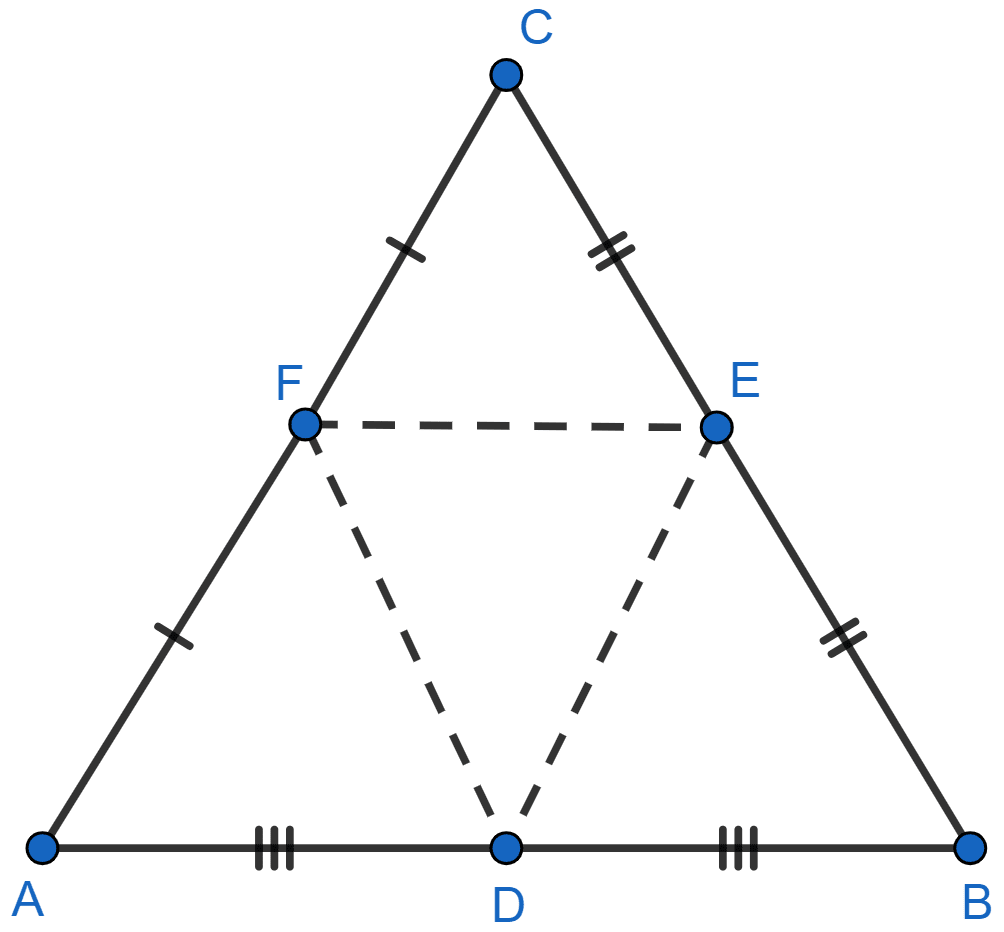
In △ABC,

D, E and F are mid-points of AB, BC and CA respectively.

Now join DE, EF and FD.

To prove :

△ADF ≅ △DBE ≅ △ECF ≅ △DEF

In △ABC,

D and E are midpoints of AB and BC

∴ DE || AC or,

DE || FC .......(i)

or DE || AF .........(ii)

D and F are midpoints of AB and AC

∴ DF || BC or,

DF || EC .......(iii)

or DF || BE ........(iv)

F and E are midpoints of AC and BC

∴ FE || AB or,

FE || AD .......(v)

or FE || DB (vi)

From (i) and (iii) we get,

DE || FC and DF || EC.

∴ DECF is a parallelogram.

We know that,

Diagonal FE divides the parallelogram DECF in two congruent triangles DEF and CEF.

∴ △DEF ≅ △ECF .......(1)

From (ii) and (v) we get,

DE || AF and FE || AD.

∴ ADEF is a parallelogram.

We know that,

Diagonal FD divides the parallelogram in two congruent triangles DEF and AFD.

∴ △DEF ≅ △AFD .......(2)

From (iv) and (vi) we get,

DF || BE and FE || DB.

∴ DBEF is a parallelogram.

We know that,

Diagonal DE divides the parallelogram in two congruent triangles DEF and DBE.

∴ △DEF ≅ △DBE .......(3)

Using equations 1, 2 and 3 we get,

△ADF ≅ △DBE ≅ △ECF ≅ △DEF.

Hence, proved that four triangles formed by joining in pairs, the mid-points of the sides of a triangle are congruent to each other.

If D, E and F are mid-points of the sides AB, BC and CA respectively of an isosceles triangle, ABC, prove that △DEF is also isosceles.

Answer

It is given that,

ABC is an isosceles triangle. Let AB = AC = x.

D, E and F are mid-points of the sides AB, BC and CA respectively.

Join D, E and F.

D and E are midpoints of AB and BC

∴ DE || AC and DE = $\dfrac{1}{2}$AC = $\dfrac{x}{2}$. (By midpoint theorem) ......(i)

F and E are midpoints of AC and BC

∴ FE || AB and FE = $\dfrac{1}{2}$AB = $\dfrac{x}{2}$. (By midpoint theorem) ......(ii)

From (i) and (ii) we get, DE = FE.

Hence, proved that △DEF is an isosceles triangle.

The diagonals AC and BD of a parallelogram ABCD intersect at O. If P is the mid-point of AD, prove that

(i) PO || AB

(ii) PO = $\dfrac{1}{2}$CD.

Answer

(i) Given,

ABCD is a parallelogram in which diagonals AC and BD intersect each other at O, P is the midpoint of AD.

Join OP.

In parallelogram, diagonals bisect each other,

∴ BO = OD.

Here, O is the mid-point of BD.

In △ABD,

P and O are midpoints of AD and BD respectively,

PO || AB and PO = $\dfrac{1}{2}$AB (By midpoint theorem) ......(i)

Hence, proved that PO || AB.

(ii) ABCD is a parallelogram.

∴ AB = CD .......(ii)

Using both (i) and (ii) we get,

PO = $\dfrac{1}{2}$AB = $\dfrac{1}{2}$CD.

Hence, proved that PO = $\dfrac{1}{2}$CD.

In the adjoining figure, ABCD is a quadrilateral in which P, Q, R and S are midpoints of AB, BC, CD and DA respectively. AC is its diagonal. Show that

(i) SR || AC and SR = $\dfrac{1}{2}$AC

(ii) PQ = SR

(iii) PQRS is a parallelogram.

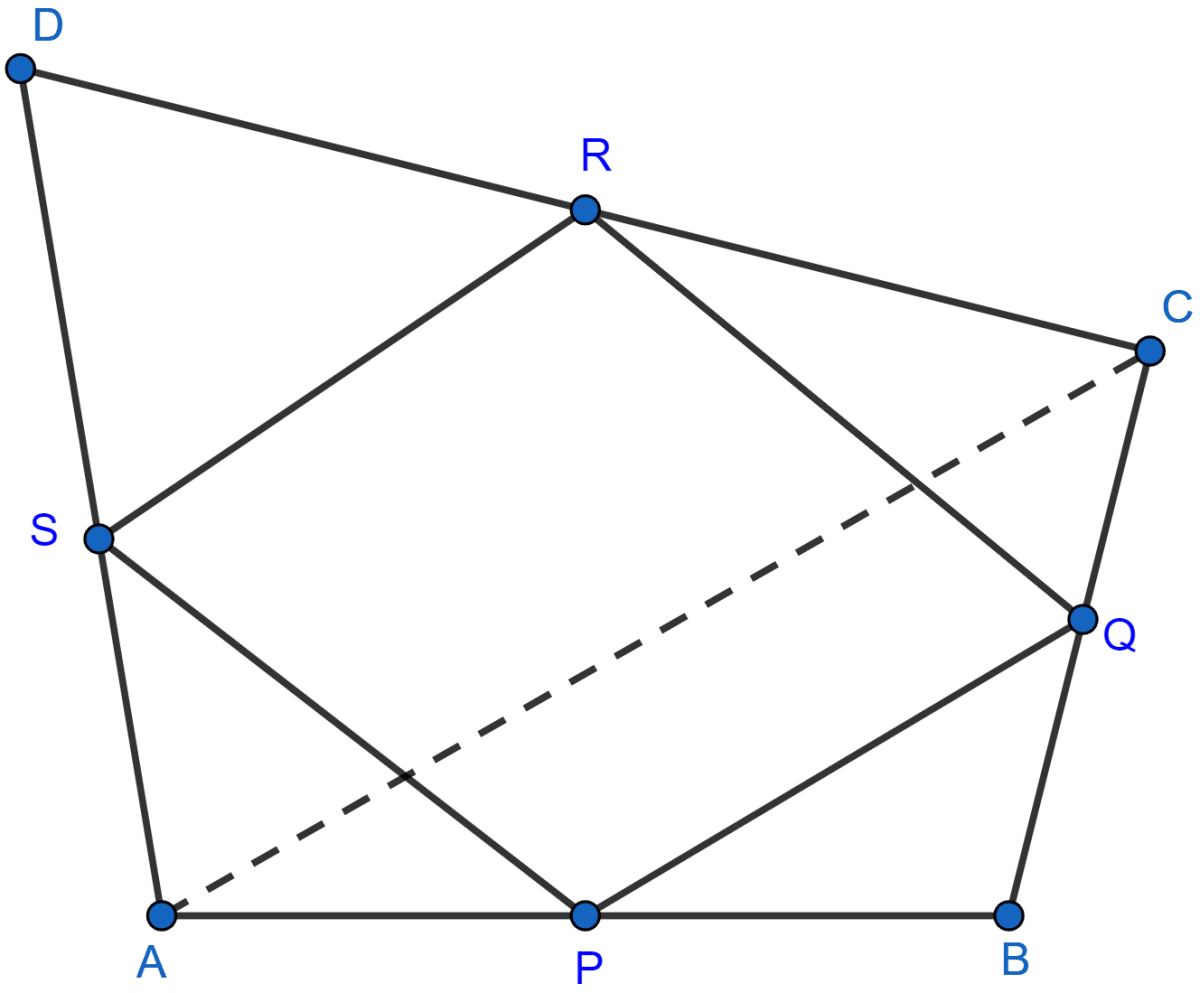
Answer

(i) In △ADC,

S and R are midpoints of AD and DC respectively,

∴ SR || AC and SR = $\dfrac{1}{2}$AC (By mid-point theorem) .....(i)

Hence, proved that SR || AC and SR = $\dfrac{1}{2}$AC (By mid-point theorem).

(ii) In △ABC,

P and Q are midpoints of AB and BC,

PQ || AC and PQ = $\dfrac{1}{2}$AC .......(ii)

Using (i) and (ii) we get,

PQ = SR and PQ || SR.

Hence, proved that PQ = SR.

(iii) Since, PQ = SR and PQ || SR.

Hence, proved that PQRS is a parallelogram.

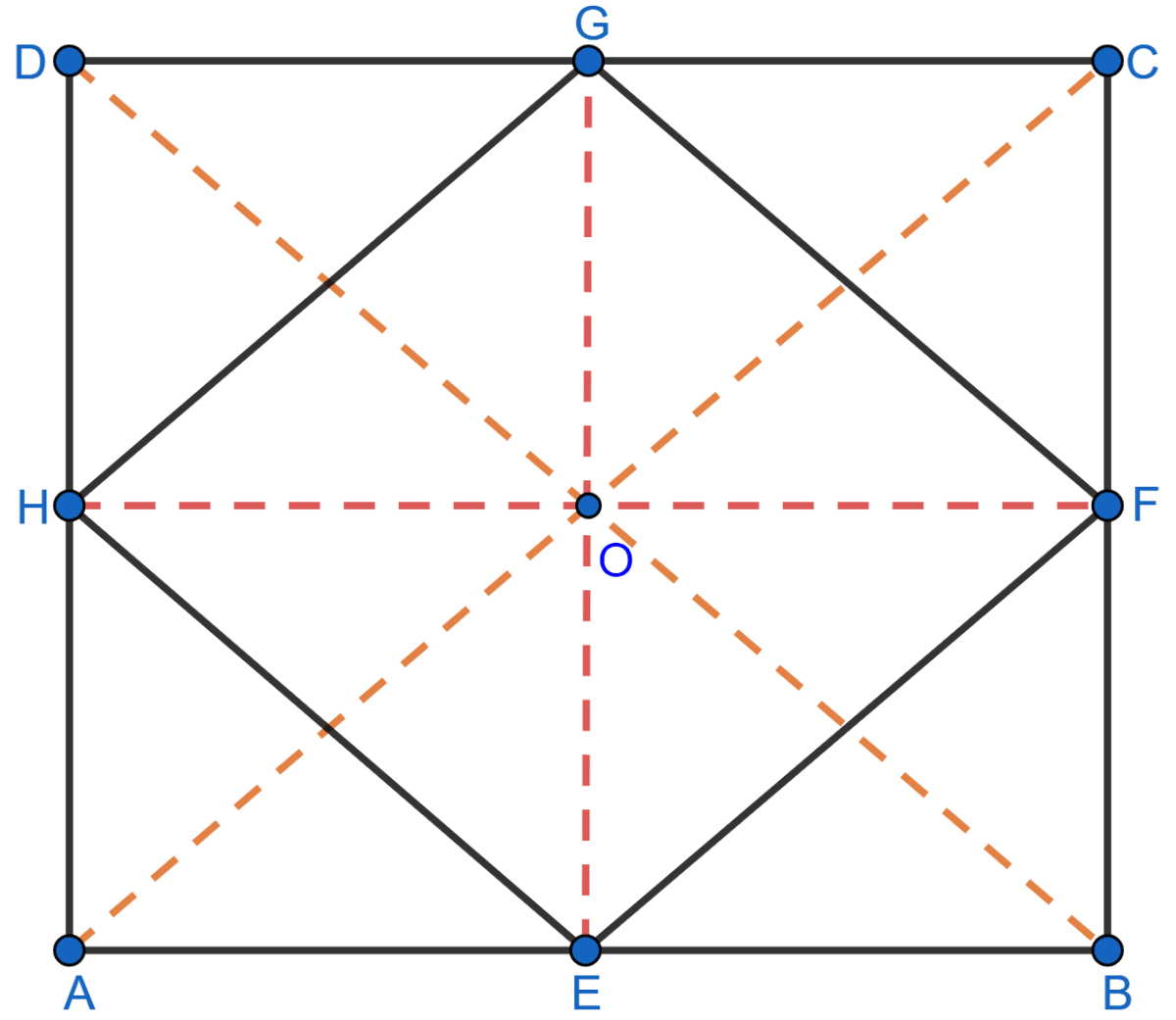
Show that the quadrilateral formed by joining the mid-points of the adjacent sides of a square, is also a square.

Answer

Let ABCD be a square in which E, F, G and H are midpoints of AB, BC, CD and DA respectively.

Join EF, FG, GH and HE.

Join AC and BD.

In △ACD,

G and H are mid-points of CD and AD respectively,

∴ GH || AC and GH = $\dfrac{1}{2}$AC .......(i)

In △ABC,

E and F are mid-points of AB and BC respectively,

∴ EF || AC and EF = $\dfrac{1}{2}$AC .......(ii)

Using (i) and (ii) we get,

EF || GH and EF = GH = $\dfrac{1}{2}$AC ........(1)

In △ABD,

E and H are mid-points of AB and AD respectively,

∴ EH || BD and EH = $\dfrac{1}{2}$BD .......(iii)

In △BCD,

G and F are mid-points of CD and BC respectively,

∴ FG || BD and FG = $\dfrac{1}{2}$BD .......(iv)

Using (iii) and (iv) we get,

EH || FG and EH = FG = $\dfrac{1}{2}$BD ........(2)

We know that diagonals of square are equal,

AC = BD

Dividing both sides by 2 we get,

$\dfrac{\text{AC}}{2} = \dfrac{\text{BD}}{2}$

Substituting above value in 1 and 2 we get,

EF = GH = EH = FG .........(v)

∴ EFGH is a parallelogram.

In △GOH and △GOF,

OH = OF as diagonals of parallelogram bisect each other.

OG = OG (Common)

GH = GF (From (v))

∴ △GOH ≅ △GOF (SSS axiom of congruency)

∠GOH = ∠GOF (c.p.c.t.c.)

From figure,

⇒ ∠GOH + ∠GOF = 180°

⇒ ∠GOH + ∠GOH = 180°

⇒ 2∠GOH = 180°

⇒ ∠GOH = 90°.

So, the diagonals of EFGH bisect and are perpendicular to each other.

∴ EFGH is a square.

Hence, proved that quadrilateral formed by joining the mid-points of the adjacent sides of a square, is also a square.

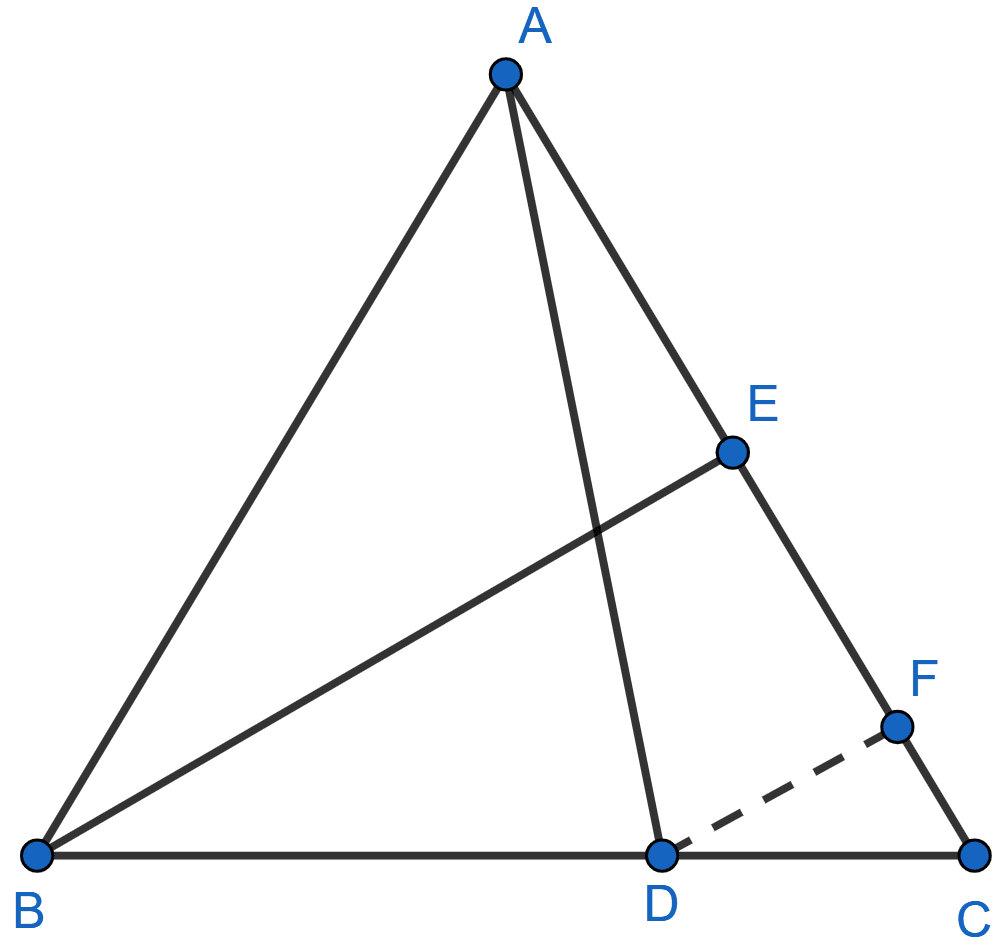
In the adjoining figure, AD and BE are medians of △ABC. If DF || BE, prove that CF = $\dfrac{1}{4}AC.$

Answer

In △BCE,

D is the midpoint of BC (As AD is median)

DF || BE

∴ F is the midpoint of CE (By converse of mid-point theorem).

⇒ CF = $\dfrac{1}{2}CE$ .......(i)

Given,

BE is median

∴ CE = $\dfrac{1}{2}AC$

Substituting value of CE in (i) we get,

$\Rightarrow CF = \dfrac{1}{2}CE \\[1em] \Rightarrow CF = \dfrac{1}{2} \times \dfrac{1}{2}AC \\[1em] \Rightarrow CF = \dfrac{1}{4}AC.$

Hence, proved that $CF = \dfrac{1}{4}AC.$

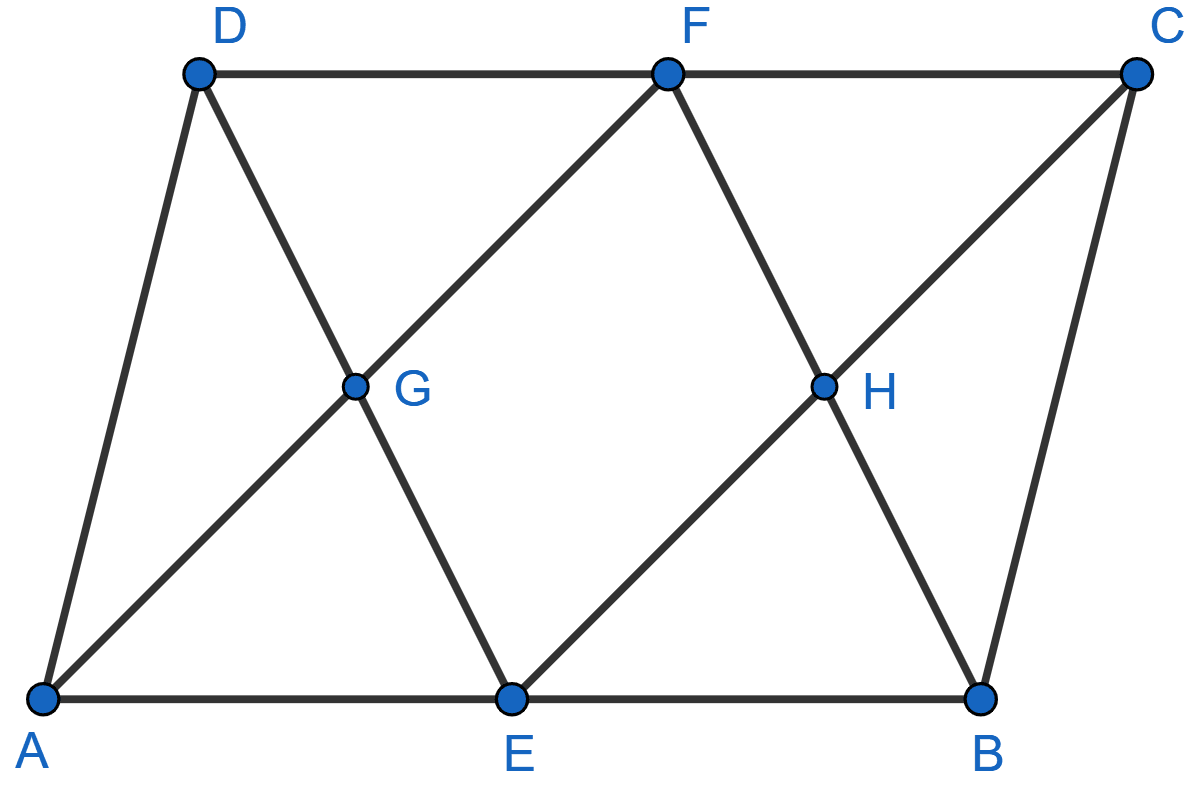
In the adjoining figure, ABCD is a parallelogram. E and F are mid-points of the sides AB and CD respectively. The straight lines AF and BF meet the straight lines ED and EC in points G and H respectively. Prove that

(i) △HEB ≅ △HCF

(ii) GEHF is a parallelogram.

Answer

(i) We know that,

ABCD is a parallelogram,

∴ FC || BE

∠CEB = ∠FCE (Alternate angles)

⇒ ∠HEB = ∠FCH .......(1)

∠EBF = ∠CFB (Alternate angles)

⇒ ∠EBH = ∠CFH .......(2)

Here E and F are mid-points of AB and CD

BE = $\dfrac{1}{2}$AB ........(3)

CF = $\dfrac{1}{2}$CD ........(4)

We know that ABCD is a parallelogram,

AB = CD

Now dividing both sides by $\dfrac{1}{2}$

$\dfrac{1}{2}$AB = $\dfrac{1}{2}$CD

Using equations 3 and 4 we get,

BE = CF .......(5)

In △HEB and △HCF,

∠HEB = ∠FCH (Using eqn. i)

∠EBH = ∠CFH (Using eqn. ii)

BE = CF (Using eqn. v)

∴ △HEB ≅ △HCF (By ASA axiom of congruency)

Hence, proved that △HEB ≅ △HCF.

(ii) AB = CD (As ABCD is a parallelogram)

Hence, AE = CF (As E and F are mid-points of the sides AB and CD respectively)

As, AB || CF we can say that,

AE || CF

Since, AE = CF and AE || CF

∴ AECF is a parallelogram.

∴ AF || EC

From figure we get,

GF || EH ........(1)

AB = CD (As ABCD is a parallelogram)

Hence, DF = EB (As E and F are mid-points of the sides AB and CD respectively) and DF || EB.

Since, DF = EB and DF || EB

∴ DEBF is a parallelogram.

∴ DE || FB

From figure we get,

GE || FH ........(2)

From 1 and 2 we get,

GF || EH and GE || FH.

∴ GEHF is a parallelogram.

Hence, proved that GEHF is a parallelogram.

ABC is an isosceles triangle with AB = AC. D, E and F are mid-points of the sides BC, AB and AC respectively. Prove that line segment AD is perpendicular to EF and is bisected by it.

Answer

From figure,

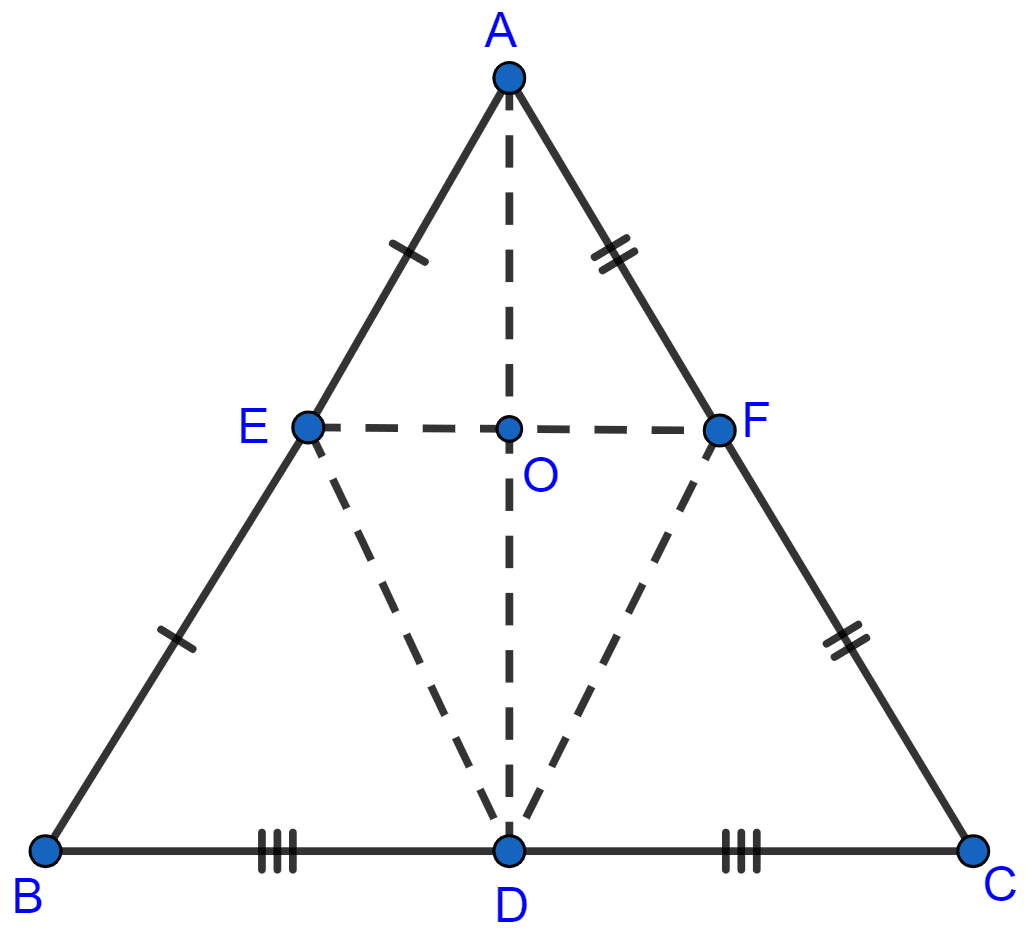
In △ABD and △ACD,

△ABC is an isosceles triangle

∴ ∠ABD = ∠ACD

Here D is the mid-point of BC

BD = CD

It is given that AB = AC

∴ △ABD ≅ △ACD (By SAS axiom of congruency)

⇒ ∠ADB = ∠ADC (By c.p.c.t.c)

From figure,

⇒ ∠ADB + ∠ADC = 180°
⇒ ∠ADB + ∠ADB = 180°
⇒ 2∠ADB = 180°
⇒ ∠ADB = 90°.

So, AD is perpendicular to BC.

D and E are mid-points of BC and AB,

By midpoint theorem,

DE || AC or,

DE || AF .......(i)

D and F are mid-points of BC and AC,

By midpoint theorem,

DF || AB or,

DF || AE .......(ii)

Using (i) and (ii) we get,

AEDF is a parallelogram.

Diagonals of parallelogram bisect each other

AD and EF bisect each other.

Since, E and F are mid-points of AB and AC,

By midpoint theorem,

EF || BC

Since, AD is perpendicular to BC and EF || BC.

∴ AD ⊥ EF.

Hence, proved that line segment AD is perpendicular to EF and is bisected by it.

In the quadrilateral given below, AB || DC, E and F are mid-points of AD and BD respectively. Prove that

(i) G is the mid-point of BC

(ii) EG = $\dfrac{1}{2}$(AB + DC).

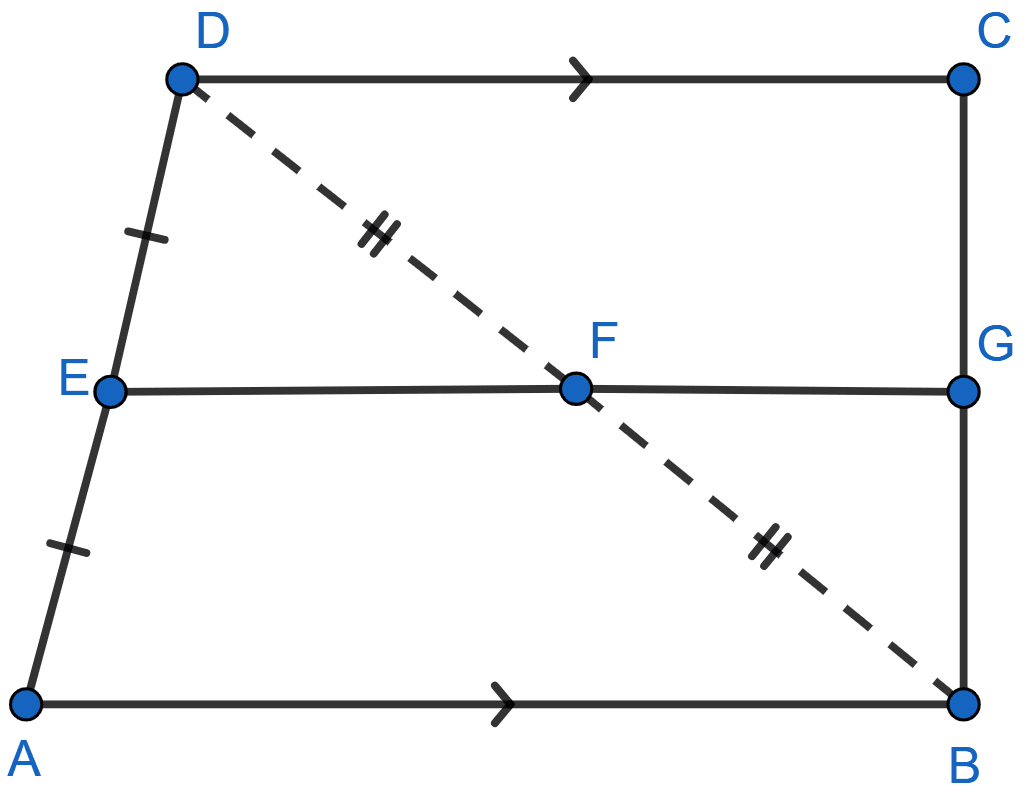
Answer

(i) In △ABD,

E is mid-point of AD and F is mid-point of BD,

∴ EF || AB and EF = $\dfrac{1}{2}$AB .......(1)

Given,

AB || CD

Since, EF || AB and AB || CD

⇒ EF || CD

⇒ EG || CD.

Since, EG || CD we can say,

In △BCD,

⇒ FG || CD

Given, F is midpoint of BD and FG || CD

∴ G is the midpoint of BC. (By converse of mid-point theorem)

Hence, proved that G is the midpoint of BC.

(ii) In △BCD,

F and G are midpoint of BD and BC respectively,

FG = $\dfrac{1}{2}$CD ..........(2)

Adding eqn. (1) from part (i) and eqn (2) we get,

EF + FG = $\dfrac{1}{2}$AB + $\dfrac{1}{2}$CD

EG = $\dfrac{1}{2}$(AB + CD).

Hence, proved that EG = $\dfrac{1}{2}$(AB + CD).

In the quadrilateral given below, AB || DC || EG. If E is mid-point of AD, prove that

(i) G is midpoint of BC

(ii) 2EG = AB + CD

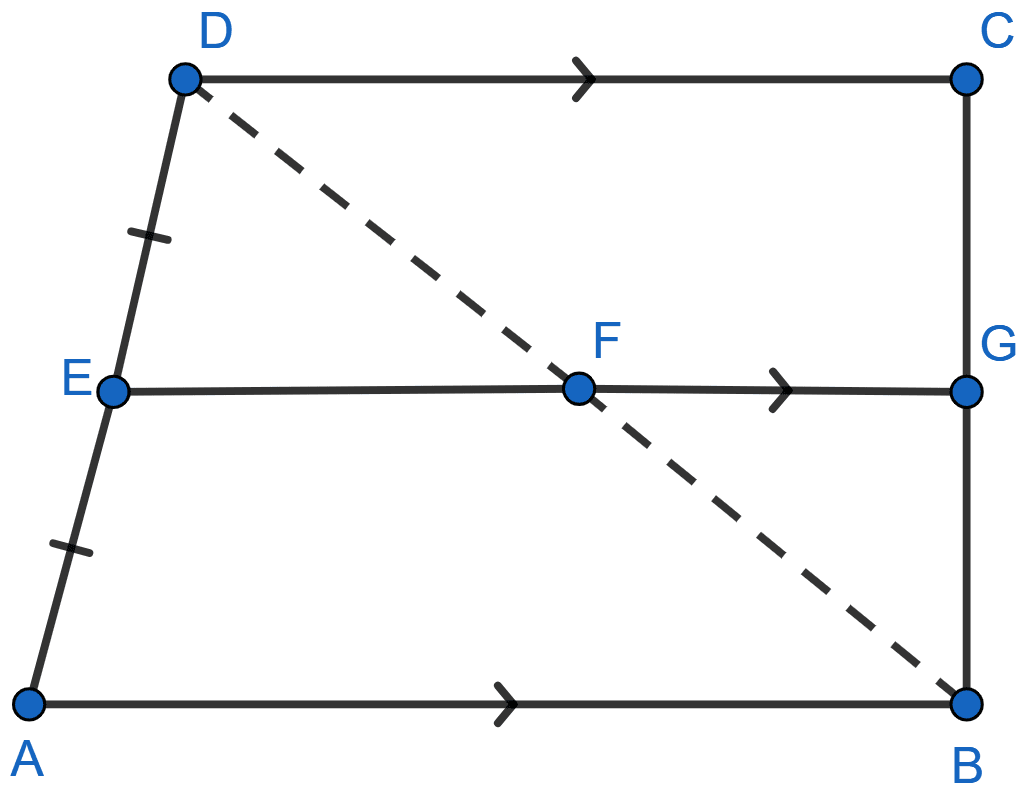
Answer

(i) Given,

EG || AB, we can say that

⇒ EF || AB

In △DAB,

E is midpoint of AD and EF || AB

∴ F is midpoint of BD (By converse of mid-point theorem).

EF = $\dfrac{1}{2}$AB .......(1)

Given,

EG || DC we can say that,

FG || DC

In △BCD,

F is midpoint of BD and FG || DC

∴ G is midpoint of BC (By converse of mid-point theorem).

Hence, proved that G is midpoint of BC.

(ii) In △BCD,

F is midpoint of BD and G is midpoint of BC

∴ FG = $\dfrac{1}{2}$DC .......(2)

Adding eqn. 1 from part (i) and eqn. 2 we get,

EF + FG = $\dfrac{1}{2}$AB + $\dfrac{1}{2}$DC

EG = $\dfrac{1}{2}$(AB + CD)

2EG = AB + CD.

Hence, proved that 2EG = AB + CD.

In the quadrilateral given below, AB || DC. E and F are mid-points of non-parallel sides AD and BC respectively. Calculate :

(i) EF if AB = 6 cm and DC = 4 cm

(ii) AB if DC = 8 cm and EF = 9 cm.

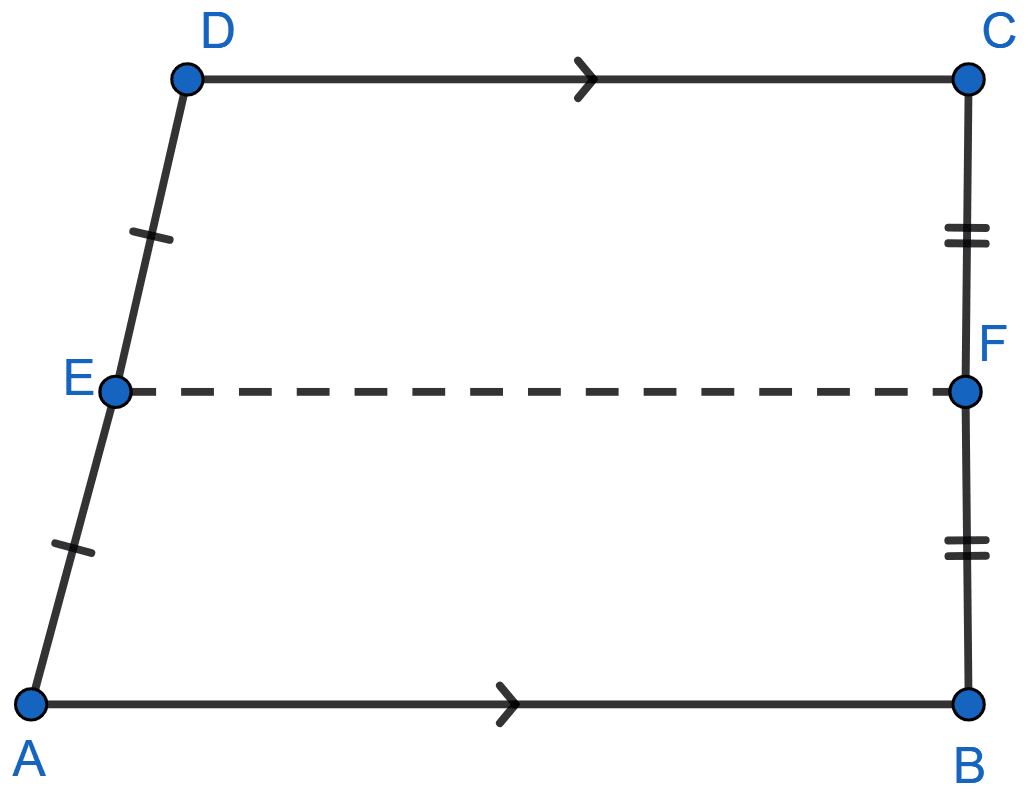
Answer

ABCD is a trapezium in which AB || DC and E, F are mid-points of AD and BC respectively.

Join CE and produce it to meet BA produced at G.

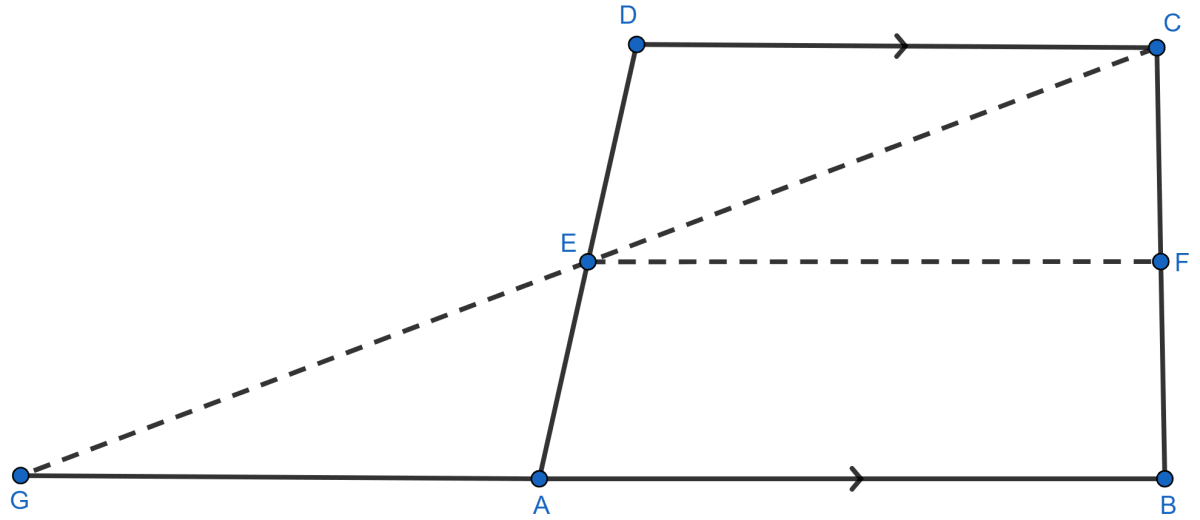
In △EDC and △EAG,

ED = EA (∵ E is mid-point of AD)

∠CED = ∠ GEA (Vertically opposite ∠s)

∠ECD = ∠EGA (Alternate ∠s)

∴ △EDC ≅ △EAG

⇒ CD = GA and EC = EG (c.p.c.t.)

In △CGB,

E is mid-point of CG

F is mid-point of BC

∴ By mid-point theorem, EF || AB and EF = $\dfrac{1}{2}$GB.

But GB = GA + AB = CD + AB

∴ EF = $\dfrac{1}{2}$(AB + CD) .....(1)

(i) Given,

AB = 6 cm and DC = 4 cm,

Putting these values in eq (1) we get,

EF = $\dfrac{1}{2}$(6 + 4)

= $\dfrac{1}{2}$ x 10

= 5 cm

Hence, EF = 5 cm.

(ii) Given,

DC = 8 cm and EF = 9 cm

Putting these values in eq (1) we get,

9 = $\dfrac{1}{2}$(AB + 8)

⇒ 18 = AB + 8

⇒ AB = 18 - 8 = 10 cm

Hence, AB = 10 cm.

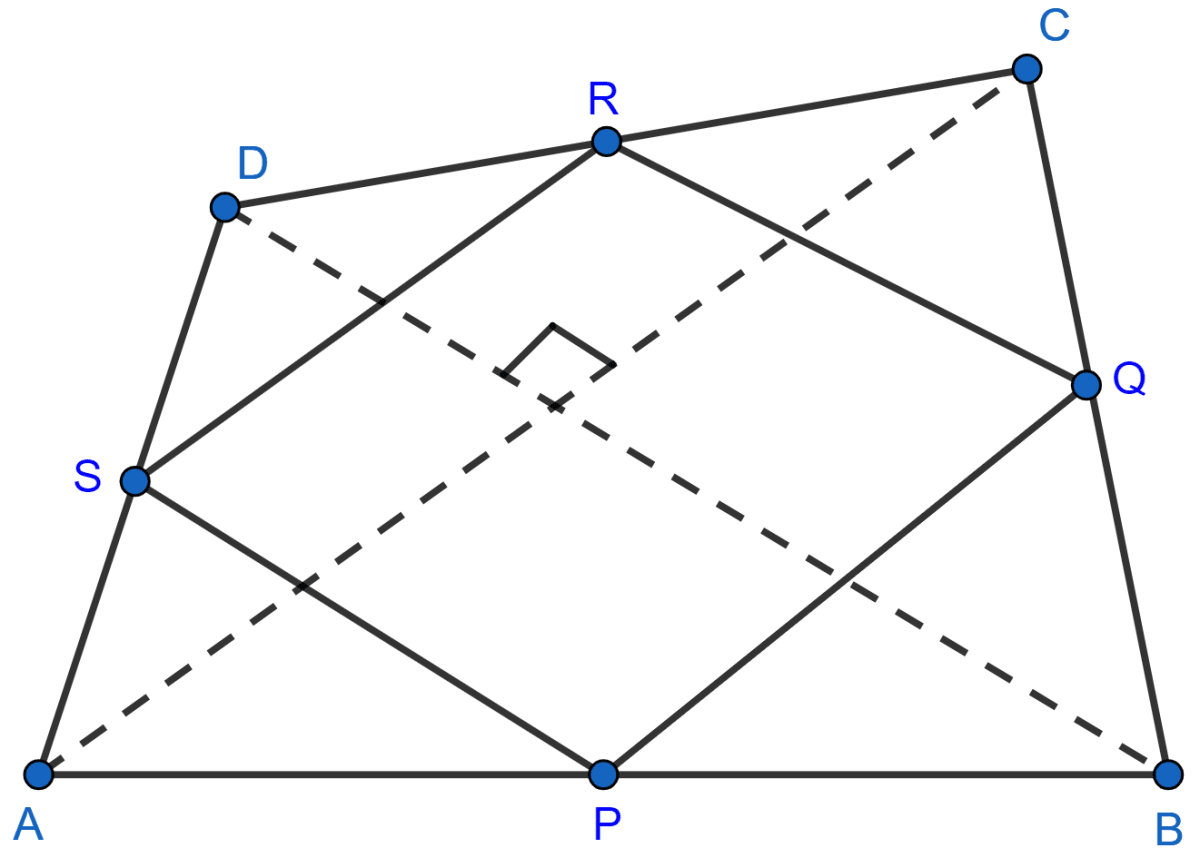
In the quadrilateral given below, AD = BC, P, Q, R and S are mid-points of AB, BD, CD and AC respectively. Prove that PQRS is a rhombus.

Answer

It is given that,

In △ABD,

P and Q are mid-points of AB and BD,

PQ || AD and PQ = $\dfrac{1}{2}$AD = $\dfrac{1}{2}$BC .......(i)

In △ACD,

R and S are mid-points of CD and AC,

RS || AD and RS = $\dfrac{1}{2}$AD = $\dfrac{1}{2}$BC .......(ii)

In △BCD,

R and Q are mid-points of CD and BD,

RQ || BC and RQ = $\dfrac{1}{2}$BC .......(iii)

In △ABC,

P and S are mid-points of AB and AC,

PS || BC and PS = $\dfrac{1}{2}$BC .......(iv)

From (i) and (ii) we get,

PQ || RS

From (iii) and (iv) we get,

RQ || PS

From (i), (ii), (iii) and (iv) we get,

PQ = RS = PS = RQ.

Since, all sides are equal and opposite sides are parallel.

Hence, proved that PQRS is a rhombus.

In the figure given below, ABCD is a kite in which BC = CD, AB = AD. E, F, G are mid-points of CD, BC and AB respectively. Prove that :

(i) ∠EFG = 90°

(ii) The line drawn through G and parallel to FE bisects DA.

Answer

Construction,

1. Join AC and BD

2. AC and BD intersect at O.

3. Join EF and FG.

(i) We know that,

Diagonals of a kite intersect at right angles.

∠MON = 90° .......(i)

In △BCD,

E and F are mid-points of CD and BC,

EF || DB and EF = $\dfrac{1}{2}$DB ......(ii)

Since, EF || DB we can say that,

MF || ON.

As sum of opposite angles of a quadrilateral = 180°

∠MON + ∠MFN = 180°

90° + ∠MFN = 180°

∠MFN = 90°.

From figure,

∠EFG = ∠MFN = 90°.

Hence, proved that ∠EFG = 90°.

(ii) From part (i) we get,

FE || BD

Here line through G (GH) is parallel to FE.

∴ GH || FE

or GH || BD.

In △ABD,

GH || BD and G is midpoint of AB,

∴ H is mid-point of AD (By converse of mid-point theorem).

Hence, proved that the line drawn through G and parallel to FE bisects DA.

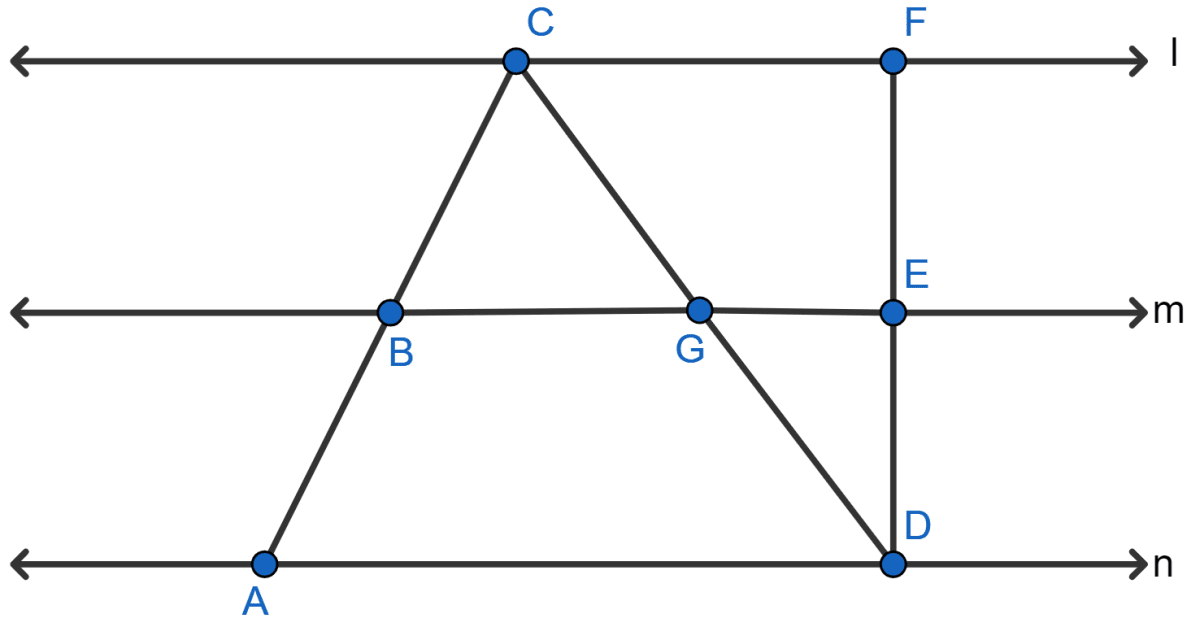
In the adjoining figure, the lines l, m and n are parallel to each other, and G is mid-point of CD. Calculate :

(i) BG if AD = 6 cm

(ii) CF if GE = 2.3 cm

(iii) AB if BC = 2.4 cm

(iv) ED if FD = 4.4 cm

Answer

(i) In △ACD,

G is mid-point of CD and BG is parallel to AD,

∴ B is mid-point of AC (By converse of mid-point theorem).

By mid-point theorem,

BG = $\dfrac{1}{2}$AD = $\dfrac{1}{2}$ x 6 = 3 cm.

Hence, BG = 3 cm.

(ii) In △CDF,

G is mid-point of CD and GE || CF

∴ E is mid-point of FD (By converse of mid-point theorem).

By mid-point theorem,

GE = $\dfrac{1}{2}$CF

CF = 2GE

CF = 2(2.3) = 4.6 cm

Hence, CF = 4.6 cm.

(iii) From part (i)

B is mid-point of AC,

∴ AB = BC

Hence, AB = 2.4 cm

(iv) From part (ii),

E is mid-point of FD,

∴ ED = $\dfrac{1}{2}$FD = $\dfrac{1}{2}$ x 4.4 = 2.2 cm

Hence, ED = 2.2 cm

In a △ABC, AB = 3 cm, BC = 4 cm and CA = 5 cm. If D and E are mid-points of AB and BC respectively, then the length of DE is

1. 1.5 cm

2. 2 cm

3. 2.5 cm

4. 3.5 cm

Answer

Since, D is midpoint of AB and E is midpoint of BC,

DE || AC and DE = $\dfrac{1}{2}$AC = $\dfrac{1}{2}$ x 5 = 2.5 cm

Hence, Option 3 is the correct option.

In the adjoining figure, ABCD is a rectangle in which AB = 6 cm and AD = 8 cm. If P and Q are mid-points of the sides BC and CD respectively, then the length of PQ is

1. 7 cm

2. 5 cm

3. 4 cm

4. 3 cm

Answer

Length of diagonal (BD) of ABCD = $\sqrt{AB^2 + AD^2} = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100}$ = 10 cm.

In △BCD,

P is midpoint of BC and Q is midpoint of CD.

PQ || BD and PQ = $\dfrac{1}{2}$BD = $\dfrac{1}{2}$ x 10 = 5 cm.

Hence, Option 2 is the correct option.

D and E are mid-points of the sides AB and AC of △ABC and O is any point on the side BC. O is joined to A. If P and Q are mid-points of OB and OC respectively, then DEQP is

1. a square

2. a rectangle

3. a rhombus

4. a parallelogram

Answer

In △ABC,

D and E are respective midpoints of AB and AC.

∴ DE || (BC or PQ) ......(1)

Again in △ABO,

D and P are respective midpoints of AB and BO.

∴ DP || AO ........(2)

In △ACO,

E and Q are respective midpoints of AC and CO.

∴ EQ || AO ........(3)

From 2 and 3 we get,

DP || EQ .......(4)

From 1 and 4 we get,

DE || PQ and DP || EQ

∴ DEQP is a parallelogram.

Hence, Option 4 is the correct option.

The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rectangle if

1. PQRS is a parallelogram

2. PQRS is a rectangle

3. the diagonals of PQRS are perpendicular to each other

4. the diagonals of PQRS are equal.

Answer

Let ABCD be a quadrilateral with P, Q, R and S as mid-points of AB, BC, CD and DA respectively.

Let PR ⊥ QS.

In △QRP,

A and B are midpoints of PQ and QR respectively.

∴ AB || PR and AB = $\dfrac{1}{2}PR$ (By midpoint theorem) ........(1)

Similarly in △PRS,

D and C are midpoints of PS and RS respectively.

∴ DC || PR and DC = $\dfrac{1}{2}PR$ (By midpoint theorem) ........(2)

In △PQS,

D and A are midpoints of PS and PQ respectively.

∴ DA || QS and DA = $\dfrac{1}{2}QS$ (By midpoint theorem).........(3)

Similarly in △QRS,

B and C are midpoints of QR and SR respectively.

∴ BC || QS and BC = $\dfrac{1}{2}QS$ (By midpoint theorem).........(4)

From 1 and 2 we get,

AB = DC and AB || DC

From 3 and 4 we get,

DA = BC and DA || BC

Hence, proved that ABCD is a parallelogram.

Since, DA || QS and PR ⊥ QS

∴ DA ⊥ PR.

Since, DC || PR and PR ⊥ QS

∴ DC ⊥ QS.

In OMDN,

∠OMD = ∠SMC (Vertically opposite angle are equal)

In quadrilateral sum of angles = 360°

∠O + ∠M + ∠N + ∠D = 360°

90° + 90° + 90° + ∠D = 360°

∠D = 360° - 270° = 90°.

In parallelogram sum of alternate angles = 180°.

∠D + ∠B = 180°

90° + ∠B = 180°

∠B = 90°

Since, opposite sides are equal and adjacent sides are perpendicular to each other.

Hence, ABCD is a rectangle.

The quadrilateral formed by joining the mid-points of the sides of a quadrilateral ABCD, taken in order, is a rectangle if the diagonals of PQRS are perpendicular to each other.

Hence, Option 3 is the correct option.

The quadrilateral formed by joining the mid-points of the sides of a quadrilateral ABCD, taken in order is a rhombus if

1. ABCD is a parallelogram

2. ABCD is a rhombus

3. the diagonals of ABCD are equal

4. the diagonals of ABCD are perpendicular to each other.

Answer

Let ABCD be a quadrilateral with P, Q, R and S as mid-points of AB, BC, CD and DA respectively.

Let diagonals be of equal length i.e. AC = BD = x

In △BCA,

P and Q are midpoints of AB and BC respectively.

∴ PQ || AC and PQ = $\dfrac{1}{2}$AC = $\dfrac{1}{2}$x (By midpoint theorem) ........(1)

Similarly in △ACD,

S and R are midpoints of AD and CD respectively.

∴ SR || AC and SR = $\dfrac{1}{2}$AC = $\dfrac{1}{2}$x (By midpoint theorem) ........(2)

In △ABD,

S and P are midpoints of AD and AB respectively.

∴ SP || BD and SP = $\dfrac{1}{2}$BD = $\dfrac{1}{2}$x (By midpoint theorem).........(3)

Similarly in △BCD,

Q and R are midpoints of BC and CD respectively.

∴ QR || BD and QR = $\dfrac{1}{2}$BD = $\dfrac{1}{2}$x (By midpoint theorem).........(4)

From 1, 2, 3 and 4 we get,

PQ = SR = SP = QR.

Hence, proved that PQRS is a rhombus.

∴ The quadrilateral formed by joining the mid-points of the sides of a quadrilateral ABCD, taken in order is a rhombus if the diagonals of ABCD are equal.

Hence, Option 3 is the correct option.

The figure formed by joining the mid-points of the sides of a quadrilateral ABCD, taken in order, is a square only if

1. ABCD is a rhombus

2. diagonals of ABCD are equal

3. diagonals of ABCD are perpendicular to each other

4. diagonals of ABCD are equal and perpendicular to each other.

Answer

Let ABCD be a quadrilateral with P, Q, R and S as mid-points of AB, BC, CD and DA respectively.

Let diagonals be of equal length i.e. AC = BD = x and AC ⊥ BD.

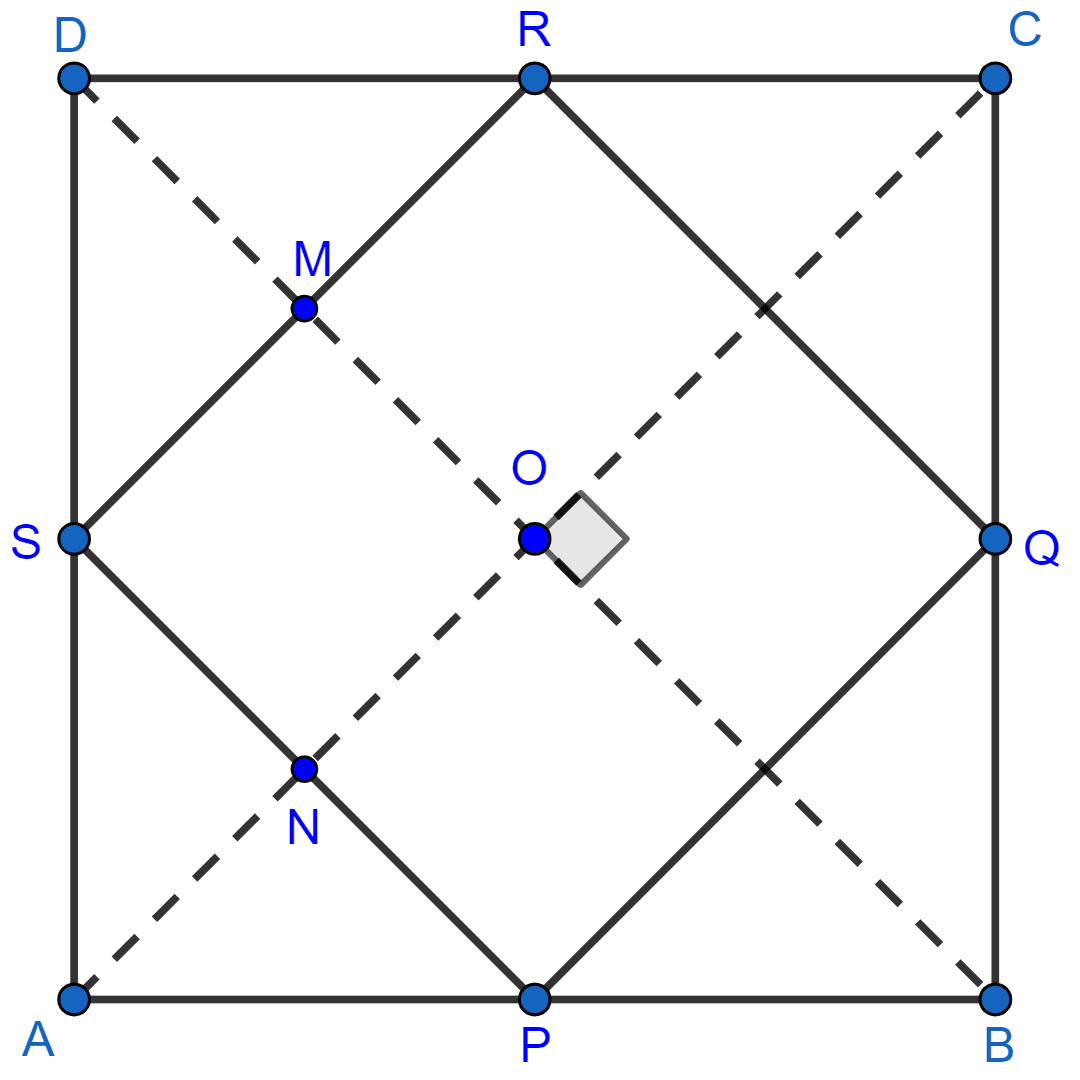
In △BCA,

P and Q are midpoints of AB and BC respectively.

∴ PQ || AC and PQ = $\dfrac{1}{2}AC = \dfrac{1}{2}x$ (By midpoint theorem) ........(1)

Similarly in △ACD,

S and R are midpoints of AD and CD respectively.

∴ SR || AC and SR = $\dfrac{1}{2}AC = \dfrac{1}{2}x$ (By midpoint theorem) ........(2)

In △ABD,

S and P are midpoints of AD and AB respectively.

∴ SP || BD and SP = $\dfrac{1}{2}BD = \dfrac{1}{2}x$ (By midpoint theorem).........(3)

Similarly in △BCD,

Q and R are midpoints of BC and CD respectively.

∴ QR || BD and QR = $\dfrac{1}{2}BD = \dfrac{1}{2}x$ (By midpoint theorem).........(4)

From 1, 2, 3 and 4 we get,

PQ = SR = SP = QR.

Hence, proved that PQRS is a rhombus.

Since, SP || BD and AC ⊥ BD

∴ SP ⊥ AC.

Since, SR || AC and AC ⊥ BD

∴ SR ⊥ BD.

In OMSN,

∠OMS = ∠DMR (Vertically opposite angle are equal)

In quadrilateral sum of angles = 360°

∠O + ∠M + ∠N + ∠S = 360°

90° + 90° + 90° + ∠S = 360°

∠S = 360° - 270° = 90°.

Since, in rhombus adjacent angles sum = 180°

∠S + ∠R = 180°

90° + ∠R = 180°

∠R = 90°.

∠Q + ∠R = 180°

90° + ∠Q = 180°

∠Q = 90°.

∠S + ∠P = 180°

90° + ∠P = 180°

∠P = 90°.

Since, PQ = QR = RS = SP and ∠P = ∠Q = ∠R = ∠S = 90°

Hence, proved that PQRS is a square.

The figure formed by joining the mid-points of the sides of a quadrilateral ABCD, taken in order, is a square only if diagonals of ABCD are equal and perpendicular to each other.

Hence, Option 4 is the correct option.

Consider the following two statements:

Statement 1: The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

Statement 2: The line through the mid-point of one side of a triangle and parallel to another side bisects the third side.

Which of the following is valid?

1. Both the statements are true.

2. Both the statements are false.

3. Statement 1 is true, and Statement 2 is false.

4. Statement 1 is false, and Statement 2 is true.

Answer

According to statement 1 :

The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

This statement describes mid-point theorem.

∴ Statement 1 is true.

According to statement 2 :

The line through the mid-point of one side of a triangle and parallel to another side bisects the third side.

This statement describes the converse of mid-point theorem.

∴ Statement 2 is true.

Hence, option 1 is the correct option.

Assertion (A): For a Δ ABC, line segment EF is drawn such that E is the midpoint of AB and F is a midpoint of AC. Then the quadrilateral formed EFCB is a trapezium.

Reason (R): The line segment joining the midpoint of two sides of a triangle is parallel to the third side.

1. Assertion (A) is true, Reason (R) is false.

2. Assertion (A) is false, Reason (R) is true.

3. Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).

4. Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).

Answer

According to the Midpoint Theorem:

"The line segment joining the midpoints of any two sides of a triangle is parallel to the third side and is equal to half of its length."

∴ Reason (R) is true.

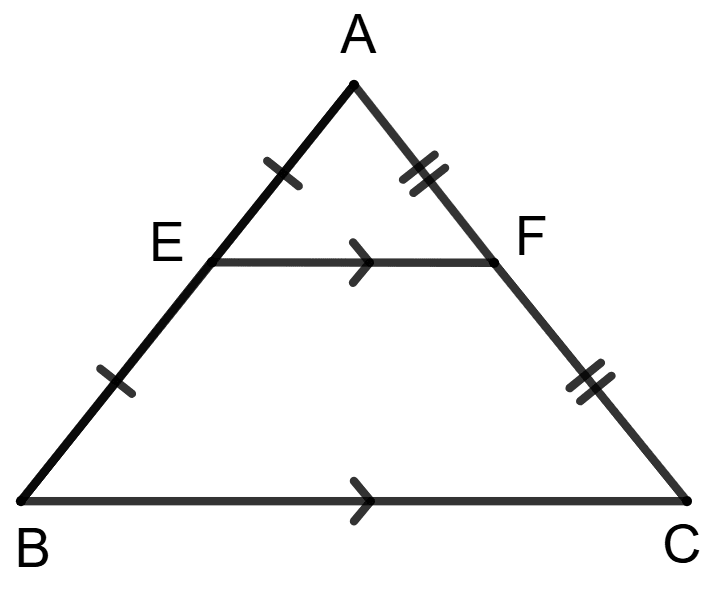
In △ABC:

⇒ E is the midpoint of AB.

⇒ F is the midpoint of AC.

The line segment joining E and F is EF.

Therefore, by the Midpoint Theorem, EF ∥ BC.

The quadrilateral EFCB has one pair of parallel sides (EF and BC).

Therefore, the quadrilateral EFCB is indeed a trapezium.

∴ Assertion (A) is true.

∴ Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason (or explanation) for Assertion (A).

Hence, option 3 is the correct option.

Assertion (A): In a Δ DEF, we have DE = EF = DF = 6 cm. A line segment PQ is drawn parallel to DF such that EP = 3 cm. Then we can conclude that PQ = 3 cm.

Reason (R): Any line segment drawn inside a triangle parallel to the base of the triangle cuts the removing two sides in half.

1. Assertion (A) is true, Reason (R) is false.

2. Assertion (A) is false, Reason (R) is true.

3. Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).

4. Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).

Answer

According to converse of mid-point theorem, the straight line drawn through the mid-point of one side of a triangle parallel to another bisects the third side.

It is given that PQ is drawn parallel to DF. And, EP = 3 cm.

∴ P is midpoint of ED.

Therefore, Q will also be mid-point of EF.

According to Midpoint Theorem states that the line segment joining the midpoints of any two sides of a triangle is parallel to the third side and is equal to half of it.

PQ = $\dfrac{1}{2}$ x DF = $\dfrac{1}{2}$ x 6 cm

Thus, PQ = 3 cm.

∴ Assertion (A) is true.

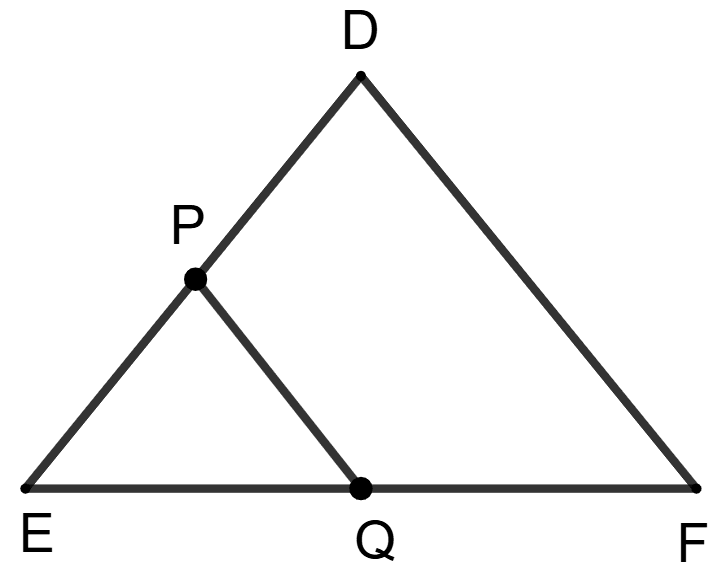
A line segment parallel to the base does not necessarily cut the other two sides in half unless it passes through the midpoints.

∴ Reason (R) is false.

∴ Assertion (A) is true, Reason (R) is false.

Hence, option 1 is the correct option.

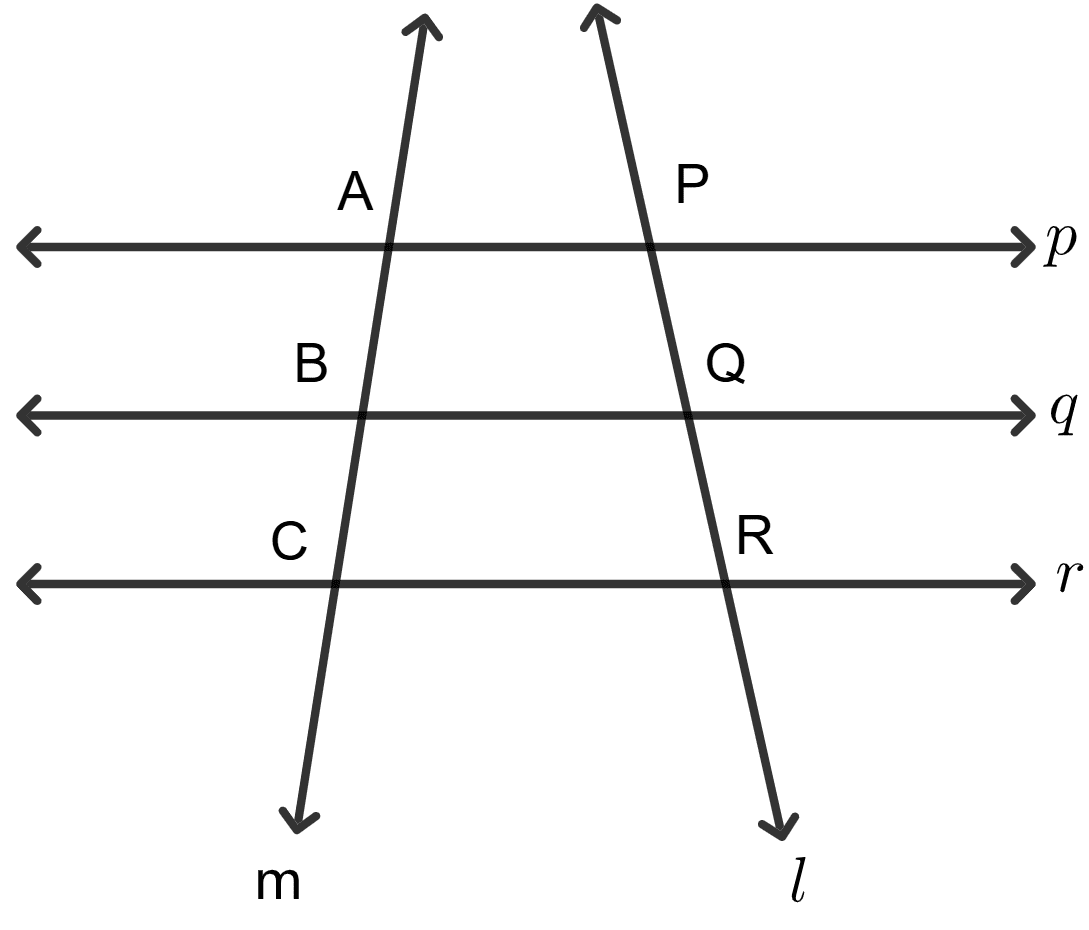
Assertion (A): Refer to the adjoining figure. Three lines p, q, r are parallel to each other and PQ = QR = 1 cm. Then we conclude that AB = $\dfrac{1}{2}$ AC.

Reason (R): If a tranversal makes equal intercepts on three parallel lines, then another transversal will also make equal intercepts.

1. Assertion (A) is true, Reason (R) is false.

2. Assertion (A) is false, Reason (R) is true.

3. Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason for Assertion (A).

4. Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct reason (or explanation) for Assertion (A).

Answer

According to equal intercept theorem, if a tranversal makes equal intercepts on three or more parallel lines, then any other line cutting them will also make equal intercepts.

∴ Reason (R) is true.

Three lines p, q, r are parallel to each other

PQ = QR = 1 cm.

⇒ PQ = QR

By equal intercept theorem.

⇒ AB = BC

From figure, AC = AB + BC

⇒ AC = AB + AB

⇒ AC = 2AB

⇒ AB = $\dfrac{1}{2}$ AC.

∴ Assertion (A) is true.

∴ Both Assertion (A) and Reason (R) are true, and Reason (R) is the correct reason (or explanation) for Assertion (A).

Hence, option 3 is the correct option.

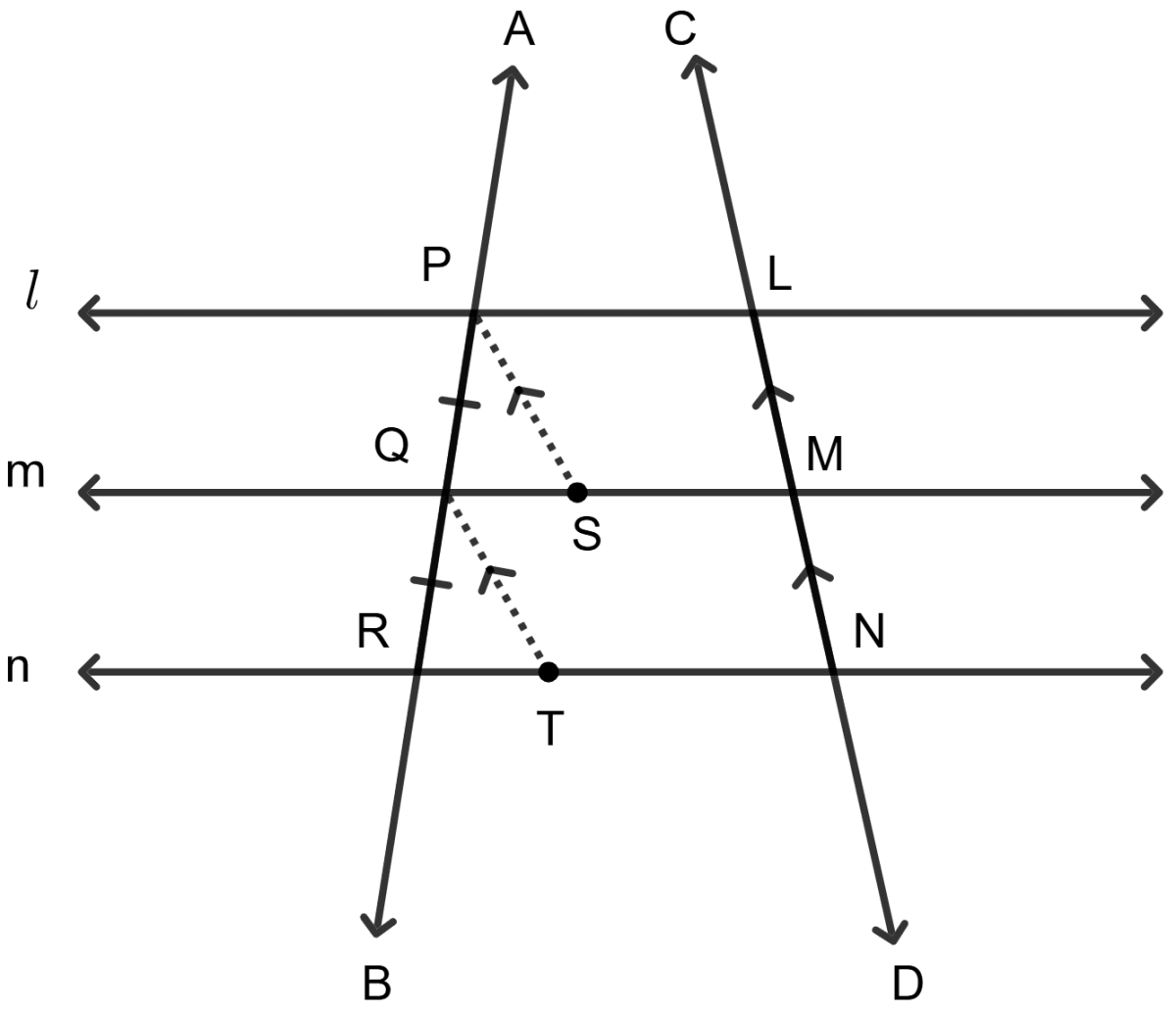
ABCD is a rhombus with P, Q and R as mid-points of AB, BC and CD respectively. Prove that PQ ⊥ QR.

Answer

Join AC and BD.

Diagonals of rhombus intersect at right angle.

∠MON = 90°

In △BCD,

Q and R are mid-points of BC and CD.

RQ || DB and RQ = $\dfrac{1}{2}$DB

RQ || DB ⇒ MQ || ON

From figure,

∠MON + ∠MQN = 180° (Sum of alternate angles of quadrilateral = 180°)

∠MQN = 180° - 90° = 90°

∴ PQ ⊥ QR.

Hence, proved that PQ ⊥ QR.

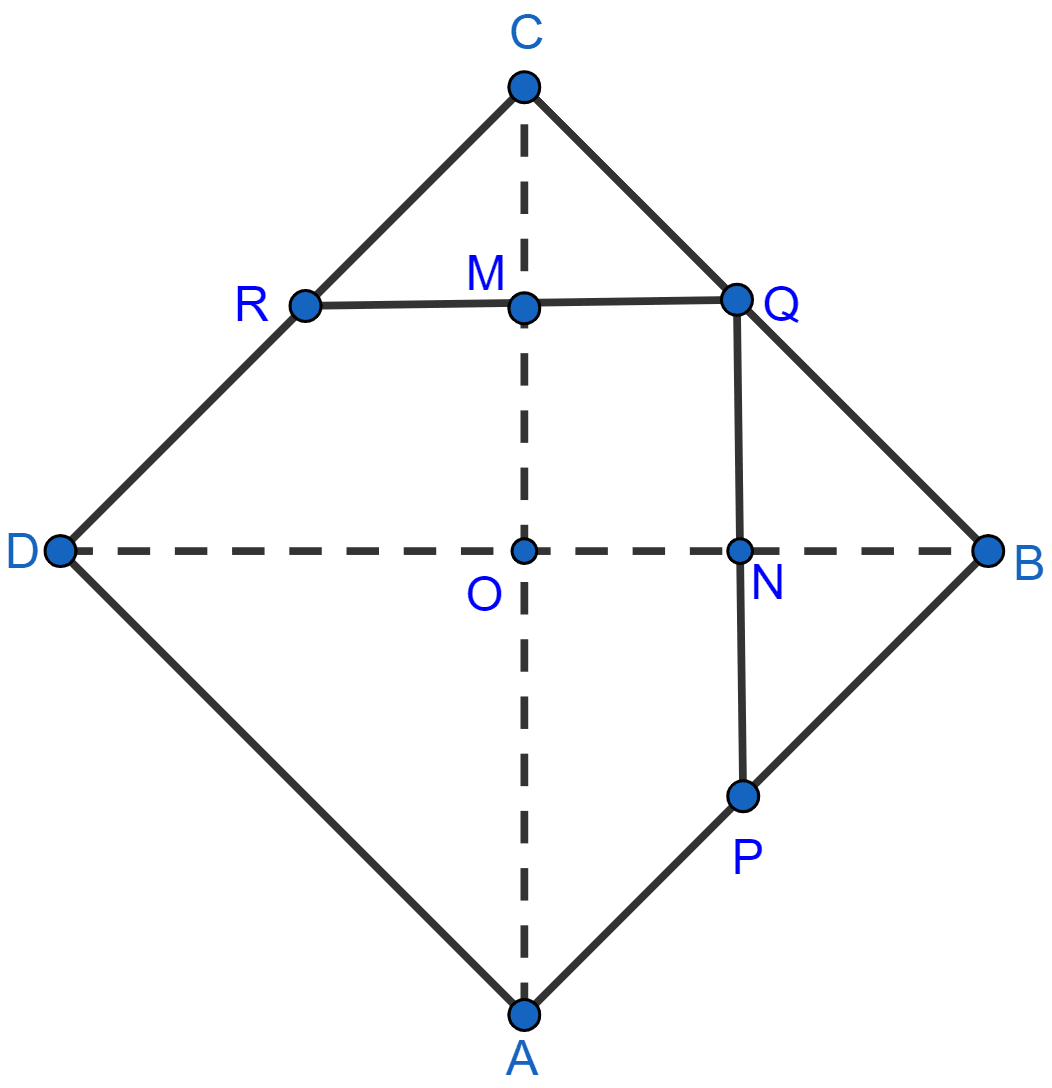
The diagonals of a quadrilateral ABCD are perpendicular. Show that the quadrilateral formed by joining the mid-points of its adjacent sides is a rectangle.

Answer

From figure,

ABCD is a quadrilateral in which diagonals AC and BD are perpendicular to each other. P, Q, R and S are mid-points of AB, BC, CD and DA.

In △ABC,

P and Q are mid-points of AB and BC respectively,

PQ || AC and PQ = $\dfrac{1}{2}$AC .......(1) (By mid-point theorem)

In △ADC,

S and R are mid-points of AD and DC respectively,

SR || AC and SR = $\dfrac{1}{2}$AC .........(2) (By mid-point theorem)

Using eqn. 1 and 2 we get,

PQ || SR and PQ = SR.

So, PQRS is a parallelogram.

In △ABD,

S and P are mid-points of AD and AB respectively,

SP || BD and SP = $\dfrac{1}{2}$BD .........(3) (By mid-point theorem)

Given,

AC and BD intersect at right angles,

From 3 we get,

SP || BD.

∴ SP ⊥ AC

From 2 we get,

SR || AC

∴ SP ⊥ SR i.e. ∠RSP = 90°.

∴ PQRS is a rectangle.

Hence, proved that the quadrilateral formed by joining the mid-points of its adjacent sides is a rectangle.

If D, E and F are mid-points of the sides BC, CA and AB respectively of a △ABC, prove that AD and FE bisect each other.

Answer

△ABC with D, E and F as mid-points of the sides BC, CA and AB is shown below:

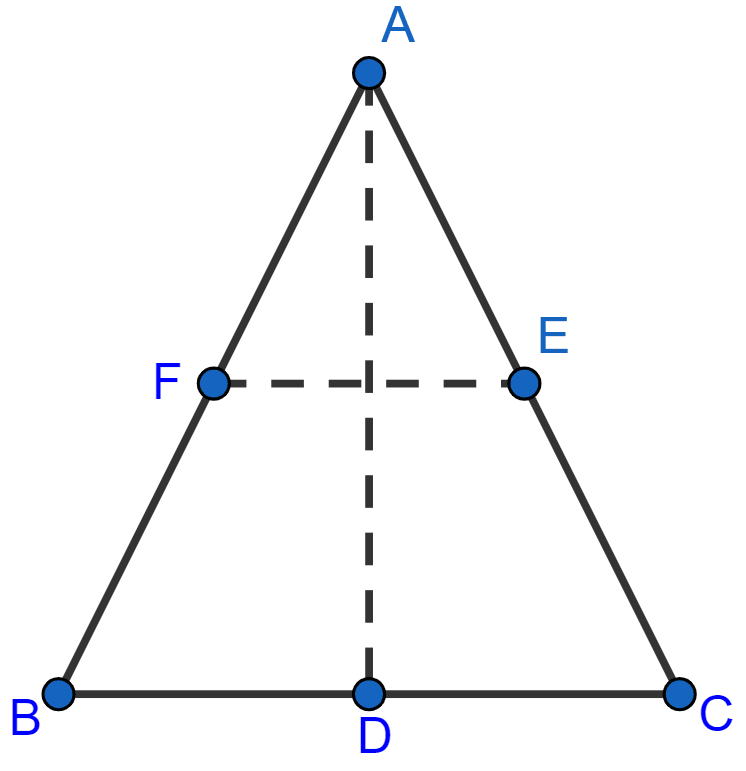
D and E are midpoints of BC and CA respectively,

DE = $\dfrac{1}{2}$AB and DE || AB or DE || AF .......(1)

Since,

F is midpoint of AB,

AF = $\dfrac{1}{2}$AB

∴ AF = DE .......(2)

F and D are midpoints of AB and BC respectively,

FD = $\dfrac{1}{2}$AC and FD || AC or FD || AE .......(3)

Since,

E is midpoint of AC,

AE = $\dfrac{1}{2}$AC

∴ FD = AE .......(4)

From 1, 2, 3 and 4 we get,

DE || AF, AF = DE and FD || AE, FD = AE.

Hence, AEDF is a parallelogram.

∴ AD and EF bisect each other.

Hence, AD and EF bisect each other.

In △ABC, D and E are mid-points of the sides AB and AC respectively. Through E, a straight line is drawn parallel to AB to meet BC at F. Prove that BDEF is a parallelogram. If AB = 8 cm and BC = 9 cm, find the perimeter of the parallelogram BDEF.

Answer

Since, D and E are mid-points of AB and AC respectively,

DE || BC or DE || BF and DE = $\dfrac{1}{2}$BC ......(By midpoint theorem) .....(i)

Given, through E, a straight line is drawn parallel to AB to meet BC at F.

F will be mid-point of BC (By converse of mid-point theorem).

Since, F is midpoint of BC,

∴ BF = $\dfrac{1}{2}$BC .....(ii)

From (i) and (ii) we get,

DE = BF and DE || BF.

Since, F and E are mid-points of BC and AC respectively,

FE || AB or FE || BD and FE = $\dfrac{1}{2}$AB ......(By midpoint theorem) .....(iii)

Since, D is midpoint of AB,

∴ BD = $\dfrac{1}{2}$AB .....(iv)

From (iii) and (iv) we get,

BD = FE and BD || FE.

Since, DE = BF, DE || BF and BD = FE, BD || FE

Hence, proved that BDEF is a parallelogram.

Perimeter of BDEF = BD + DE + FE + BF = BD + DE + BD + FE = 2(BD + FE).

BD = $\dfrac{1}{2}$AB = $\dfrac{1}{2}(8)$ = 4 cm.

FE = $\dfrac{1}{2}$BC = $\dfrac{1}{2}(9)$ = 4.5 cm.

Perimeter of BDEF = 2(BD + FE) = 2(4 + 4.5) = 2 × 8.5 = 17 cm.

Hence, perimeter of BDEF = 17 cm.

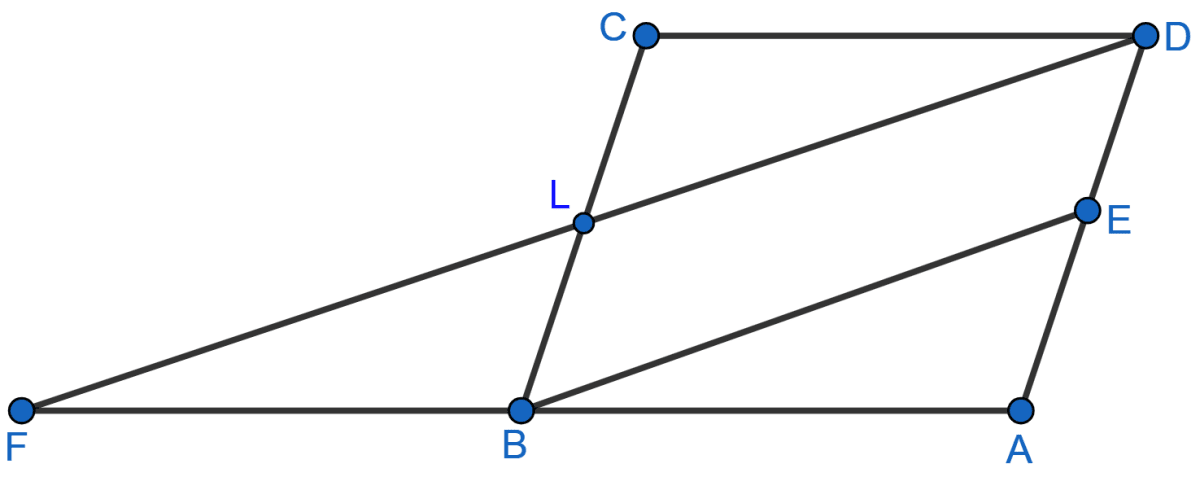
In the adjoining figure, ABCD is a parallelogram and E is mid-point of AD. DL || EB meets AB produced at F. Prove that B is mid-point of AF and EB = LF.

Answer

Given, DL || EB.

Since, DL || BE we can say that,

⇒ BE || DF

In △AFD,

E is midpoint of AD and BE is parallel to DF,

∴ B is midpoint of AF (By converse of midpoint theorem).

In BEDL,

LD || BE and BL || DE

∴ BEDL is a parallelogram.

Since, BEDL is a parallelogram opposite sides are equal.

Let LD = BE = x.

E is midpoint of AD and B is the midpoint of AF

By midpoint theorem,

BE = $\dfrac{1}{2}$FD

FD = 2BE = 2x.

LF = FD - LD = 2x - x = x.

Since, LF = BE = x.

Hence, proved that B is midpoint of AF and EB = LF.

In the adjoining figure, ABCD is a parallelogram. If P and Q are mid-points of sides CD and BC respectively. Show that CR = $\dfrac{1}{4}$AC.

Answer

In parallelogram, diagonals bisect each other.

∴ AO = OC = $\dfrac{1}{2}$AC ......(i)

In △BCD,

P and Q are midpoints of CD and BC,

PQ || BD (By midpoint theorem)

Since, PQ || BD

∴ QR || BO

In △BCO,

Q is midpoint of BC and QR || BO

∴ R is midpoint of OC

CR = $\dfrac{1}{2}$OC

Substituting value of OC from (i) in above equation,

CR = $\dfrac{1}{2}$OC = $\dfrac{1}{2} \times \dfrac{1}{2} \times$ AC = $\dfrac{1}{4}$AC.

Hence, proved that CR = $\dfrac{1}{4}$AC.