Mathematics
In a △PQR, ∠Q = 50°, ∠R = 65° and QR = 4 cm. Then PQ =
6 cm
5 cm
4 cm
3 cm
Triangles
2 Likes
Answer
In △PQR,
By angle sum property of triangle,
⇒ ∠P + ∠Q + ∠R = 180°
⇒ ∠P + 50° + 65° = 180°
⇒ ∠P + 115° = 180°
⇒ ∠P = 180° - 115°
⇒ ∠P = 65°
Since, ∠P = ∠R = 65°
⇒ PQ = QR = 4 cm (Sides opposite to equal angles in a triangle are equal)
Hence, option 3 is the correct option.
Answered By
1 Like
Related Questions
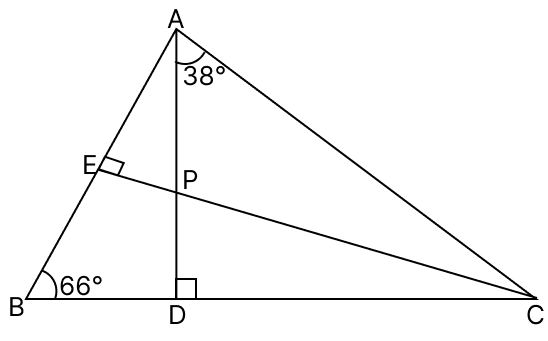
In the given figure, ∠ABC = 66°, ∠DAC = 38°. CE is perpendicular to AB and AD is perpendicular to BC. Prove that: CP > AP.
In a △ABC, AB = AC and ∠B = 50°. Then ∠A =
50°
80°
100°
105°
In the adjoining figure, ∠ABC = 90°, ∠BCA = 50° and BD ⊥ AC. Then ∠ABD =
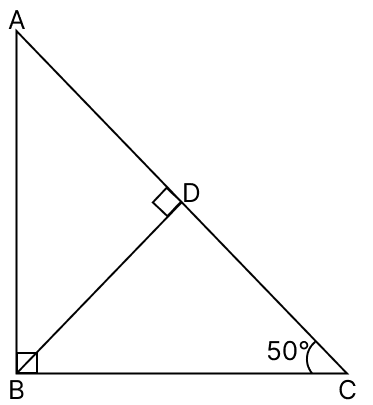
30°
40°
50°
60°
In the adjoining figure, AB = AC and BD = CD. Then, ∠ADC =
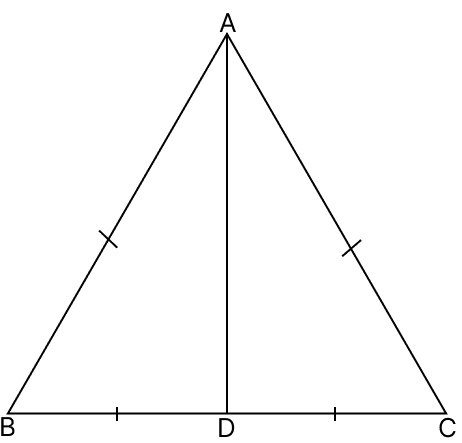
60°
75°
90°
100°